World Journal of Nuclear Science and Technology
Vol.06 No.03(2016), Article ID:68135,6 pages
10.4236/wjnst.2016.63016
The Representation of the Chemical Elements’ Isotopes by the Neutron Excess Content
Faustino Menegus
Faustino Menegus V. Europa, Bussero, Italy

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2016; accepted 8 July 2016; published 11 July 2016;
ABSTRACT
A more compact representation of the Segré chart of nuclides can be obtained replacing the isotopic neutron with the corresponding neutron excess number; a first sight inspection of all the natural isotopes is produced. The resulting representation shows a built-inorder in the organization of the nuclear components into the nuclei of the natural isotopes, sustained by the relevant role of the magic numbers. The interpretation, on the identical foot, of the nuclear instability of Tc, Pm and of the elements following Bi is suggested. The present representation reminds the spheron model of the nuclear structure suggested by L. Pauling. The alpha decay paths of radioactive isotopes are shown, side by side to the low energy nuclear transmutations (LENR). Representations of the artificial isotopes of the chemical elements and of the stellar nucleosynthesis processes are also proposed.
Keywords:
Nuclear Structure, Neutron Excess, Magic Numbers, Natural Artificial Isotopes, Stellar Nucleosynthesis

1. Introduction
The isotopes of the chemical elements are usually represented by their neutrons (N) and protons (P) content in the N, Z plane: the Segrè chart of the nuclides. A more compact representation can be achieved replacing the isotopic N number with the corresponding Neutron Excess number, NE = A − 2Z, where A represents the isotopic mass number. The new representation contains exactly the identical information of the Segrè chart but, being more compact, it allows a first sight inspection of the close to three hundred natural isotopes. Accordingly some of the features of the organization of the nuclear components into stable nuclei are readily perceived. The graphical compression equally highlights some sharp and interesting changes in the landscape of the artificial isotopes, less easily appreciated in the usual representation. Finally a different instance in which the graphical compactness of the Z-NE plane may turn useful compared to that of the N-Z plane, is the representation of the stellar nucleosynthesis processes [1] . The purpose of the present work is to stress the features of the new representations, not adequately stressed previously [2] .
2. Methods
The The Neutron Excess (NE) number of the isotope zXA of the element X was calculated by the equation NE = A − 2Z. The mas numbers A were obtained from Tuli [3] . The result is a new method in the representation of the isotopes of the chemical elements.
3. The Representation of the Natural Isotopes of the Chemical Elements
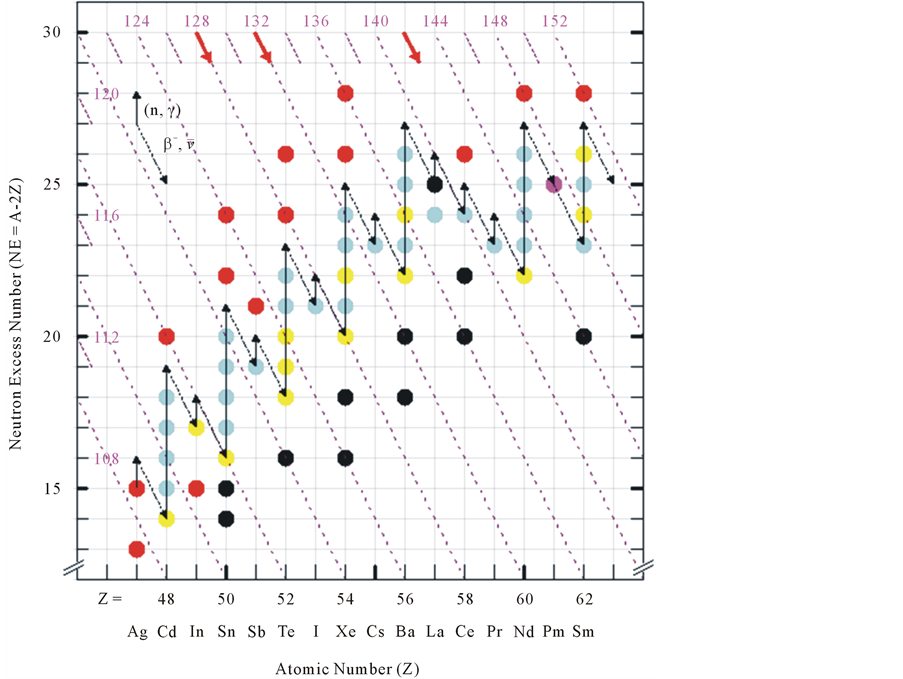
The natural isotopes of the chemical elements, from 1H to 83Bi, are represented in the Z, NE plane of Figure 1, distinguishing the even from the odd Z elements and the stable from the radioactive isotopes. The full symbols highlight the highest natural abundance isotope inside each isotopic family [4] . Elements’ isotopes are arranged on vertical arrays while isotons and isobars, with constant numbers of neutrons and constant atomic mass respectively, are arranged on oblique arrays (see Figure 1). Arrays of isotopes with magic numbers of protons or of neutrons [5] [6] are connected by yellow lines, thereafter magic lines. These lines show an identical origin on the Z axis, stressing the identity of the two sets of proton and neutron magic numbers. The maximum and the minimum NE of the Z even isotopic families are connected with black lines that represent the borders of the β stability valley. Assuming that the Z axis also represents the Z proton-neutron couples, the mass A of each isotope in Figure 1 is easily reached: on the Z axis the isotopic mass number will be A = 2Z, while for the isotopes in the plane, it will be A = 2Z + NE. Moreover, once the A of a single isotope is known, it is easy to see that the mass numbers of the nearby isotopes are automatically reached. Actually along the horizontal arrays, with constant NE, the isotopic mass number A differs by one Deuteron or by one Helion mass unit for single or double Z steps respectively. Instead on the oblique arrays, perpendicular to the isotons arrays, A will differ by one Triton unit for single Z steps. A representation of the above arrays is shown in Figure 1, together with the pathways of α, β−, and ε (electron capture or β+) decays of the radioactive isotopes. The transmutation of the chemical elements in LENR experiments (Low Energy Nuclear Transmutation) is represented by the 2d (2 Deuterons) symbol [7] . In Figure 1, examples of radioactive decays are shown, in particular the α decay sequence from Gd152 to Ce140 is drown side by side to the transmutation of Ba138 to Sm150 isotopes. Helions Deuterons and Tritons are reminiscent of the nuclear spheron model of L. Pauling [8] .
Perhaps the single most salient feature of the present representation concerns the neutron magic numbers, in particular 50 and 82 neutrons. These numbers pop out of the graphic by themselves, on the respective isoton magic lines, due to the high presence of both isotopes, of top natural abundance isotopes, and to a slide down effect treated below. Accordingly the relevance of the magic numbers in the organization of the nuclear material is patently stressed [5] [6] . The next interesting feature is represented by the arrays of 28, 50, 82 and 126 neutron magic isotopes that subdivide the natural isotopes into blocks that apparently slide down, along the respective magic isoton lines, towards the isotopic regions of lower NE content. This effect is linked to the fact that, as the Z increases, immediately after 20Ca, 36Kr, 54Xe and 82Pb there is a sudden drop of the NE content of the isotopic families, evidenced by the upper border of the β stability valley (Figure 1). Such a drop is followed by a pause and eventually by a NE increase caused by the further progress of Z. The oblique slide-down effects then, are the result of vertical (with reference to the figure) events linked to the single isotopic families, rather than to the blocks of isotopes of different elements.
The above state of affairs can be interpreted assuming that: first, the NE content of the isotopic families of the elements underlying, on the Z axis, the 20, 50, 82 and 126 magic isoton lines, for example the elements’ families from Kr to Sn in the case of the 50 neutron magic number, undergo a general NE reduction; second, such a reduction is counteracted by the NE increase required to alleviate the nuclear electrostatic repulsion induced by the progress of Z for the elements underlying the neutron magic lines. Wyle the physical grounds of the above assumptions are yet to be explained they however allow an interpretation, on an identical foot, of the nuclear
Figure 1. Representation of the natural isotopes of the chemical elements from H to Bi by their isotopic neutron excess content, NE = A − 2Z, in the Z-NE plane. The Z axis represents both the elements proton number and the related number of proton-neutron couples. Black and red symbols refer to the isotopic families of even and odd Z elements respectively; (¡), (¨) represent stable and radioactive isotopes respectively, with the full symbol indicating the top natural abundance isotope of each element; (ã) indicates the single most stable isotope of Tc and Pm. The yellow vertical end oblique lines connect the proton and the neutron magic nuclei respectively. The region comprising all the natural isotopes is bounded by black lines corresponding to the borders of the β stability valley. The top inset characterizes the positions of the isotopes corresponding to: constant NE = Helions, Deuterons; Isotopes differing by four mass numbers = Tritons; constant mass number = Isobars; constant neutron number = Isotons. In addition the direction and the extension of the α, β, ε decays, and those of the 2d transmutations are shown. Bottom inset: bosons and fermions line up on alternate arrays originating at even and odd places on the Z axis respectively.
instability of the artificial elements Tc, Pm and as well the development of the nuclear instability of the elements immediately beyond Bi; see below for these last elements. Accordingly, at Tc and Pm, both of them seven Z steps beyond Kr and Xe, there will be a balance between the NE reduction, prevailing ahead, and the NE increase prevailing behind these elements. The relatively reduced NE content of the isotopes of these elements, inasmuch as they are Z odd, typically less stable compared to the flanking Z even elements, leads to the nuclear instability observed.
Concerning the light elements up to Ca, the isotopes with the top natural abundance are lined up on the zero or on the one NE arrays stressing, as generally accepted, the minor requirement of NE to grant their nuclear stability. In the Z-NE plane bosons and fermions lay on oblique arrays originating at even and odd places respectively on the Z axis. As far as natural isotopes are concerned it is easy to ascertain, from Figure 1, that bosons outnumber fermions.
4. The Representation of Natural and Artificial Isotopes of the Chemical Elements
Figure 2 shows the collection of all the natural and artificial isotopes of the chemical elements from 1H to 103Lr, known at October 2011 [8] . Both the upper and the lower outline of the isotopes landscape shows anything but a monotonous progress, in particular beyond 54Xe. As to the upper border the horizontal stretch of isotopes with a constant NE level, from the 55Cs to the 70Yb, may suggest a correlated nuclear stabilization effect. Interestingly, this horizontal stretch of isotopes largely coincides with the electron filling of the 4f orbital of the electronic structure. It may not be just a fortuitous coincidence, representing instead a hint of the mutual influences between the nuclear and the electronic structures of atoms [9] . A fast increase of NE is required instead for the elements between Yb and Bi. The lower border of the nuclear stability area shows, beyond Bi, a sharp bimodal increase that results in the narrow stability area for the elements beyond 92U. The sharp changes presented by the borders of the nuclear stability area of Figure 2, less marked in the usual N-Z plane representation, may offer hints to the interpretation of the nuclear stability rules. It is generally accepted that the magic numbers lose their meaning outside the β stability valley [1] [10] [11] . To this regard the slide-down effect of the natural isotopes, apparently correlated to the neutron magic numbers shown before, is absent here. It is worthwhile however to stress the existence of the double magic 28Ni48, the artificial isotope with the highest neutron defect.
As in the case of Tc and Pm the development of the nuclear instability of the artificial elements beyond Bi, can be interpreted as a conflict between the NE reduction, linked to the 126 magic isoton line and the NE increase induced by the increasing nuclear proton content with the progress of Z. Figure 2 shows, for the elements beyond Bi, a sharp reduction of the NE content, with a minimum at 85At. Thereafter, as the z increases, the NE recovery is potent enough to confer a natural abundance that is a half life exceeding the solar system age, to Th and U isotopes, but not beyond these elements because of the excessive proton electrostatic repulsion. The nuclear stability minimum, however, does not coincide with the lowest NE level of 85At (half life: 8.5 hours), but instead coincides with the higher NE level of 87Fr (half life: 22 minutes) [3] . Possibly other factors, in the high mass nuclear region, may affect the nuclear stability. To this regard it must be stressed that beyond 98Cf the superior stabilizing effect of even versus odd Z proton numbers fades (Figure 2).
Figure 2. Representation of all known isotopes, natural and artificial, of the chemical elements from H to Lr in the Z-NE plane. (■) artificial are distinguished from (■) natural isotopes. (■), ( ) indicate the longest lived artificial isotope of odd and even Z elements respectively. All the other symbols as in Figure 1.
) indicate the longest lived artificial isotope of odd and even Z elements respectively. All the other symbols as in Figure 1.
5. Representation of the Stellar Nucleosynthesis Processes of the Heavier Than Iron Nuclei
The main processes of the stellar nucleosynthesis for the heavier than iron nuclei are shown, color-coded, in the Z-NE plane: red for the rapid neutron capture of the supernova explosions (r); yellow for the slow neutron capture of the extended pre explosion stellar burning phases (s); green for the cumulative processes (rs); black for the proton capture [1] (Figure 3). As far as the s process is concerned the distinction of the natural isotopes between stable and unstable, as in Figure 1, can be neglected, since the latter isotopes have half lives exceeding the solar system age. The unstable artificial isotopes fill the empty places of the Z-NE grid. Once the mass A of an isotope is known, see the isobar grid, it is easy to reach the masses of the nearby isotopes as shown before. Moreover with the help of the isobar grid, here drown only on every four Z steps, it is easy to spot the r red shielding and the s yellow shielded couples of isotopes involved in the rs mechanisms. One advantage of the Z-NE over the N-Z representation of the stellar nucleosynthesis is that an extended number of elements can be handled. It is impressing to see how selected Z odd isotopes sit in the correct place as to allow the bridging of the slow path between the Z even and odd elements. An uninterrupted journey results from lighter to heavier nuclei.
Figure 3. Representation of the stellar nucleosynthesis processes for heavier than iron nuclei. Round symbols denote the color-coded origin of the natural isotopes: red (r) rapid neutron capture; yellow (s) slow neutron capture; azure composite (rs) process; black (p) proton capture. Artificial isotopes sit in the Z-NE grid empty places. The four Z steps grid of isobars, with the corresponding mass numbers, is shown orange. The black solid lines, corresponding to the slow neutron capture by stable nuclei, end up at unstable neutron rich nuclei. The latter undergo fast β-decay, represented by the broken lines, bridging the even to the Z odd element’s isotopes in a continuous s path. () (magenta), represents the 61Pm147 isotope with a β-decay time of 2.62 years, still compatible with the slow process. The red arrows denote the direction of the decay of the neutron rich nuclei products of the (r) process.
6. Concluding Remarks
A new method for the representation of the isotopes of the chemical elements is presented. The replacement of the isotopic neutron with the isotopic neutron excess number provides a reduction to one third of the space of the Segrè chart of nuclides. A first sight inspection of all the natural isotopes is thus achieved, stressing the relevance of the magic numbers for the nucleons assembly into the stable as well as into the unstable Tc and Pm nuclei. The representation of the artificial isotopes suggests hints about likely new interactions between the nuclear and the electronic structures of atoms [9] . Finally a handy and elegant representation of the stellar nucleosynthesis processes is provided.
Acknowledgements
The author thanks Maurizio Zanardini for the graphical work.
Cite this paper
Ghandour, R.M.-R. and Li, J. (2017) Short Term Electric Load Prediction by Incorporation of Kernel into Features Extraction Regression Technique. Smart Grid and Renewable En- ergy, 8, 31-45. http://dx.doi.org/10.4236/sgre.2017.81002
References
- 1. Shaviv, G. (2012) The Synthesis of the Elements. Astrophysics and Space Science Library, Springer, Heidelberg, New York, Dordrecht, London.
- 2. Menegus, F. (2009) Nuclear and Electronic Structure of Atoms. Proceedings of the 15th International Conference on Condensed Matter Nuclear Science, Rome, 5-9 October 2009, 378-381.
- 3. Tuli, J.K. (2011) Nuclear Wallet Cards. Brookhaven National Laboratory, USA.
- 4. Lodders, K. (2003) Solar System Abundances and Condensation Temperatures of the Elements. The Astrophysical Journal, 591, 1220-1247.
http://dx.doi.org/10.1086/375492 - 5. Goeppter Mayer, M. (1963) The Shell Model. Nobel Lecture
http://www.nobelprize.org/nobel_prizes/physics/laureates/1963/mayer/lecture.html - 6. Jansen, J.H.D. (1963) Glimpses at the History of the Nuclear Structure Theory. Nobel Lecture
http://www.nobelprize.org/nobel_prizes/physics/laureates/1963/jensen/lecture.html - 7. Iwamura, Y., Itoh, T., Yamazaki, N., Kasagi, J., Terada, Y., Ishikawa, T. and Sekiba, D. (2011) Observation of Low Energy Nuclear Transmutation Reactions Induced by Deuterium Permeation through Multilayer Pd and CaO Thin Film. J. Condens. Matter Nucl. Sci., 4, 132-144.
- 8. Pauling, L. (1970) General Chemistry. Dover Publications, Inc., New York.
- 9. Filippow, D.V., Rukhadze, A.A. and Urutskoev, L.I. (2004) Effects of Atomic Electrons on Nuclear Stability and Radioactive Decay. Annales de la Fondation Louis de Broglie, 29, Hors Série 3.
- 10. Shaviv, G. (2012) The Nuclear Shell Model, the Cosmic Abundances and Why We Do Not Know How the Heavy Elements Were Synthesized. Mem. Soc. Astro. Ital., 83, 859-874.
- 11. Cook, N.D. (2010) Models of the Atomic Nucleus. Unification through a Lattice of Nucleons. 2nd Edition, Springer, Heidelberg, New York, Dordrecht, London.