World Journal of Nuclear Science and Technology
Vol.06 No.02(2016), Article ID:66082,10 pages
10.4236/wjnst.2016.62012
Direct Analytical Method to Calculate Photopeak Efficiency and Photopeak Attenuation Coefficient of NaI(Tl) Well-Type Detector
K. S. Al-Mugren1, Mahmoud I. Abbas2*, Eman M. El-Bayoumi3, N. S. Aly3
1Physics Department, Faculty of Science, Princess Nourah Bint Abdulrahaman University, Riyadh, Saudi Arabia
2Physics Department, Faculty of Science, Alexandria University, Alexandria, Egypt
3Physics & Chemistry Department, Faculty of Education, Alexandria University, Alexandria, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 March 2016; accepted 25 April 2016; published 28 April 2016
ABSTRACT
In this paper full-energy peak (photopeak) efficiency and photopeak attenuation coefficient of 3'' × 3'' NaI(Tl) well-type scintillation detector were calculated using gamma-rayisotropic radiating point sources (with photon energy: 0.245, 0.344, 0.662, 0.779, 0.964, 1.1732, 1.333 and 1.408 MeV) placed outside the detector well. These energies were obtained from 152Eu, 137Cs and 60Co. The relations between the full energy peak efficiency and photopeak attenuation coefficients, were plotted vs. photon energy at different sources to detector distance, and it found that the full energy peak efficiency decreased by increasing the distance between the source and the detector.
Keywords:
NaI(Tl) Well-Type Scintillation Detector, Full-Energy Peak Efficiency, Photopeak Attenuation Coefficient, Gamma-Ray Point Sources

1. Introduction
In this work direct mathematical formulae for measuring the full-energy peak efficiency of HPGe well-type detector are found and the values of the measured efficiencies are compared with the published works of the experimental and theoretical old methods which have a good agreement. In this new approach the path length d(θ, ϕ) is derived as a function in the polar angle θ, and the azimuthal angle ϕ. This will reduce the mathematical formulae to an easiest and compact shape. In low level gamma-ray spectroscopy, NaI(Tl) well-type scintillation detectors are extremely useful since they offer almost 4π solid angle detection. The efficiency of such detectors can be obtained, using experimental [1] - [3] , semi-empirical [4] [5] and Monte Carlo methods [6] - [9] . The present work relies on a direct mathematical method reported by Selim and Abbas [10] - [22] , which is simple and accurate. It was used successfully in the calibration of well-type and cylindrical detectors using point, plane and volumetric sources. The efficiency is calculated in terms of the geometrical parameters of the source-detector configuration and the photopeak attenuation coefficient of the incident photon. Here, we consider 8 gamma-ray energies based on three different point sources.
2. Mathematical Treatment
In our analysis, we consider only an axial point source P, as shown in Figure 1. The efficiency in this case is given by [15]
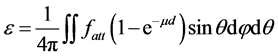 (1)
(1)
where, d is the path length traveled by a photon through the detector active medium, μ is the attenuation coefficient of the detector material, and fatt is the attenuation factor, which is given by [17]
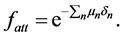 (2)
(2)
Here, μn is the attenuation coefficient of the nth absorber for the gamma-ray photon [16] , and δn is the path length of the gamma-ray photon through the nth absorber read [23] .
The polar angles, θ, are given by (see Figure 1):
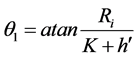 (3)
(3)
 (4)
(4)
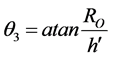 (5)
(5)
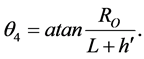 (6)
(6)
Figure 1. The well type detector configuration. The point source P, is placed on the axis of the well detector.
The distance 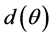 is the photon traveled distance (path length) inside the detector active volume. Several cases arise, let the gamma-ray photons enter from the inner bottom of the well. If they emerge from the outer bottom of the well, then
is the photon traveled distance (path length) inside the detector active volume. Several cases arise, let the gamma-ray photons enter from the inner bottom of the well. If they emerge from the outer bottom of the well, then 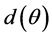 is given by:
is given by:
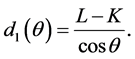 (7)
(7)
But, if they emerge from the side of the outer well, 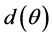 reads:
reads:
 (8)
(8)
Next, when the gamma-ray photons enter from the inner side of the well and emerge from the bottom of the outer well, we have
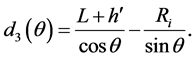 (9)
(9)
If they emerge from the side of the outer well, the photon path length is given by
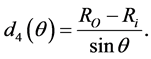 (10)
(10)
Finally, when the gamma-ray photon enters from the upper surface of the well and emerge from the bottom of the outer well, then
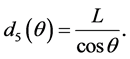 (11)
(11)
If emerging from the side of the outer well, we have

The resulting efficiency depends on the magnitudes of the polar angles. This results in the following three cases. When θ3 > θ2 > θ4 > θ1, using Equation (1) the efficiency is given by

with

Similarly, if θ3 > θ2 > θ1 > θ4

with 

3. Results and Discussions
Using the above formalism, the full-energy peak efficiency and the photopeak attenuation coefficient of 3'' × 3'' NaI(Tl) well-type scintillation detector are calculated for in the case of point sources placed outside the detector well. The 3'' × 3'' NaI(Tl) well-type model number is 802-Canberra. The dimensions of this detector are, outer radius, 3.81 cm, cavity radius, 0.858 cm, outer height, 7.62 cm, and cavity depth, 4.987 cm. The full-energy peak efficiencies are calculated using the present work and compared with those obtained by theoretical and experimental data, for various values of the source to detector distance, h', above the detector starting approximately at 20 cm up to 50 cm in a step of 5 cm.
The results of the calculations are given in Tables 1-7, along with the experimental data and the theoretical calculations based on the transfer method presented in Ref. [23] . It is clear that our theoretical results are identical to the experimental data. The error in the theoretical results of reference [23] based on the transfer method is approximately 1%. So, our present formalism consistently produces more accurate results than the other methods.
Comparing the various data in Tables 1-7, we can see that the full-energy peak efficiency decreases as the distance h' increases for the same energy of the gamma-rays. Obviously, it can be seen that the efficiency depends on the position of the source as will as it depends on the activity of the radioactive source. In Figure 2, we summarize this point by plotting the full-energy peak efficiency versus the distance h' for the eight energies of the gamma-rays. We notice the tendency that the efficiency decreases as the energy increases for the same distance as seen in Figure 2. In addition, the efficiency curves are converging at high energies. To explain these observations, we calculate the energy dependence of the attenuation coefficient.
In our formalism, the energy of the photon only enters through the dependence of the attenuation coefficient. From Equation (14), we see that the function 

Table 1. Present the photpeak efficiencies, εp, (sr) for present work, experimental and theoretical data [23] for distance h' = 20.442 cm.
Table 2. As in Table 1, for distance h' = 25.461 cm.
Table 3. As in Table 1, for distance h' = 30.537 cm.
Table 4. As in Table 1, for distance h' = 35.590 cm.
Table 5. As in Table 1, for distance h' = 40.600 cm.
Table 6. As in Table 1, for distance h' = 45.666 cm.
Table 7. Present the photopeak efficiencies, εp, (sr) for present work and experimental data [23] for distance h' = 50.717 cm.
Figure 2. The relation between the full-energy peak (photopeak) efficiency (εp) and the source to detector distance (h').
Figure 3. The relation between the photopeak attenuation coefficient (μp) and the photon energy for h' = 20.442 cm with fitting polynomial curve.
Figure 4. Similar to Figure 3 but for h' = 25.461 cm.
Figure 5. Similar to Figure 3 but for h' = 30.537 cm.
Figure 6. Similar to Figure 3 but for h' = 35.59 cm.
Figure 7. Similar to Figure 3 but for h' = 40.6 cm.
Figure 8. Similar to Figure 3 but for h' = 45.666 cm.
Figure 9. Similar to Figure 3 but for h' = 50.717 cm.
the different values of the distance considered so far. The figures also include polynomial fits up to 6th order. A common trend in μP is that it decreases rapidly at lower energies and approximately levels of at high energies about 0.05 cm−1. The sharp decrease in μP is reflected in the large change of the efficiency at low energies. However, the negligible variation of the attenuation coefficient with the gamma energy plays a smaller rule in determining the efficiency at high energies. Thus the efficiency curves converge as indicated in Figure 2.
4. Conclusion
The full-energy peak efficiency (εp) of 3'' × 3'' NaI(Tl) well-type scintillation detector, using axial point sources is calculated and compared with both the experimental and the theoretical data in Ref. [23] . In addition, the photopeak attenuation coefficients (μp) have been calculated as a function of the gamma-ray photon energy. Our formalism gives more accurate data than that of the transfer method presented in Ref. [23] . The dependence of the photopeak attenuation coefficient on the gamma energy is used to explain the variations in the efficiency as the distance between the point source and the detector changes. From the result it is clear that the full-energy peak efficiency εp decreases by increasing the distance between the detector and the source.
Cite this paper
K. S. Al-Mugren,Mahmoud I. Abbas,Eman M. El-Bayoumi,N. S. Aly, (2016) Direct Analytical Method to Calculate Photopeak Efficiency and Photopeak Attenuation Coefficient of NaI(Tl) Well-Type Detector. World Journal of Nuclear Science and Technology,06,115-124. doi: 10.4236/wjnst.2016.62012
References
- 1. Akkurt, I., Gungolu, K. and Arda, S.S. (2014) Detection Efficiency of NaI(Tl) Detector in 511-1332 keV Energy Range. Science and Technology of Nuclear Installations, 2014, Article ID: 186798.
- 2. Mavi, B. and Akkurt, I. (2010) Natural Radioactivity and Radiation Hazards in Some Building Materials Used in Isparta, Turkey. Radiation Physics and Chemistry, 79, 933-937.
http://dx.doi.org/10.1016/j.radphyschem.2010.03.019 - 3. El-Khatib, A., Badawi, M.S., Abd-Elzaher, M. and Thabet, A.A. (2012) Calculation of the Peak Efficiency for NaI(Tl) Gamma Ray Detector Using the Effective Solid Angle Method. Journal of Advanced Research in Physics, 3, Article ID: 021204.
- 4. Wang, T.K., Mar, W.Y., Ying, T.H., Liao, C.H. and Tsing, C.L. (1995) HPGe Detector Absolute-Peak-Efficiency Calibration by Using the ESOLAN Program. Applied Radiation and Isotopes, 46, 933-944.
http://dx.doi.org/10.1016/0969-8043(95)00190-O - 5. Wang, T.K., Mar, W.Y., Ying, T.H., Liao, C.H. and Tsing, C.L. (1997) HPGe Detector Efficiency Calibration for Extended Cylinder and Marinelli-Beaker Sources Using the ESOLAN Program. Applied Radiation and Isotopes, 48, 83-95.
http://dx.doi.org/10.1016/S0969-8043(96)00062-0 - 6. Radu, D. and Sima, O. (2010) Simulation of Gamma-Ray Spectra for Complex Measurement Systems Using GEANT 3.21. Romanian Reports in Physics, 62, 744-749.
- 7. Kurihara, O., Kim, E., Ueda, J., Yamada, Y., Kido, H., Oguri, T., Nemoto, S., Nemoto, M. and Akashi, M. (2011) Development of Accurate Radioactivity Assessment System for Radiation Survey with Various Detectors. Progress in Nuclear Science and Technology, 1, 248.
http://dx.doi.org/10.15669/pnst.1.248 - 8. Faddegon, B.A., Asai, M., Per, J., Ross, C., Sempau, J., Tinslay, J. and Salvat, F. (2008) Benchmarking of Monte Carlo Simulation of Bremsstrahlung from Thick Targets at Radiotherapy Energies. Medical Physics, 35, 4308.
http://dx.doi.org/10.1118/1.2975150 - 9. Jehouani, A., Ichaoui, R. and Boulkheir, M. (2000) Study of the NaI(Tl) Efficiency by Monte Carlo Method. Applied Radiation and Isotopes, 53, 887-891.
http://dx.doi.org/10.1016/S0969-8043(00)00254-2 - 10. Selim, Y.S. and Abbas, M.I. (1994) Source-Detector Geometrical Efficiency. Radiation Physics and Chemistry, 44, 1-4.
http://dx.doi.org/10.1016/0969-806X(94)90093-0 - 11. Selim, Y.S. and Abbas, M.I. (1995) Direct Calculation of the Total Efficiency of Cylindrical Scintillation Detectors for Non-Axial Point Sources. Egyptian Journal of Physics, 26, 79.
- 12. Selim, Y.S., Abbas, M.I. and Fawzy, M.A. (1998) Analytical Calculation of the Efficiencies of Gamma Scintillators. Part I: Total Efficiency for Coaxial Disk Sources. Radiation Physics and Chemistry, 53, 589-592.
http://dx.doi.org/10.1016/S0969-806X(97)00277-6 - 13. Abbas, M.I. and Basiouni, M.M. (1999) Direct Mathematical Calculation of the Photopeak Efficiency for Gamma Rays in Cylindrical NaI(Tl) Detectors. AIP Conference Proceedings, 495, 268-272.
- 14. Selim, Y.S. and Abbas, M.I. (2000) Analytical Calculations of Gamma Scintillators Efficiencies—II. Total Efficiency for Wide Coaxial Circular Disk Sources. Radiation Physics and Chemistry, 58, 15-19.
http://dx.doi.org/10.1016/S0969-806X(99)00357-6 - 15. Abbas, M.I. (2001) Analytical Formulae for Well-Type NaI (Tl) and HPGe Detectors Efficiency Computation. Applied Radiation and Isotopes, 55, 245-252.
http://dx.doi.org/10.1016/S0969-8043(01)00047-1 - 16. Abbas, M.I. (2001) HPGe Detector Photopeak Efficiency Calculation Including Self-Absorption and Coincidence Corrections for Marinelli Beaker Sources Using Compact Analytical Expressions. Applied Radiation and Isotopes, 54, 761-768.
http://dx.doi.org/10.1016/S0969-8043(00)00308-0 - 17. Abbas, M.I. (2001) A Direct Mathematical Method to Calculate the Efficiencies of a Parallelepiped Detector for an Arbitrarily Positioned Point Source. Radiation Physics and Chemistry, 60, 3-9.
http://dx.doi.org/10.1016/S0969-806X(00)00329-7 - 18. Abbas, M.I. and Selim, Y.S. (2002) Calculation of Relative Full-Energy Peak Efficiencies of Well-Type Detectors. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 480, 651-657.
http://dx.doi.org/10.1016/S0168-9002(01)01225-6 - 19. Abbas, M.I., Nafee, S. and Selim, Y.S. (2006) A Simple Mathematical Method to Determine the Efficiencies of Log-Conical Detectors. Radiation Physics and Chemistry, 75, 729-736.
http://dx.doi.org/10.1016/j.radphyschem.2005.12.034 - 20. Abbas, M.I. (2007) Direct Mathematical Method for Calculating Full-Energy Peak Efficiency and Coincidence Corrections of HPGe Detectors for Extended Sources. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 256, 554-557.
http://dx.doi.org/10.1016/j.nimb.2006.12.056 - 21. Abbas, M.I. (2010) Analytical Approach to Calculate the Efficiency of 4π NaI(Tl) Gamma-Ray Detectors for Extended Sources. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 615, 48-52.
http://dx.doi.org/10.1016/j.nima.2009.12.058 - 22. Abbas, M.I. (2010) Analytical Formulae for Borehole Scintillation Detectors Efficiency Calibration. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 622, 171-175.
http://dx.doi.org/10.1016/j.nima.2010.06.241 - 23. Gouda, M.M., Badawi, M.S., El-Khatib, A.M., Thabet, A.A., and Abbas, M.I. (2015) Calibration of Well-Type NaI(Tl) Detector Using a Point Sources Measured out the Detector Well at Different Axial Distances. Journal of Instrumentation, 10, P03022.
NOTES
*Corresponding author.












