World Journal of Nuclear Science and Technology
Vol.05 No.01(2015), Article ID:53357,15 pages
10.4236/wjnst.2015.51004
Theories in Spin Dynamics of Solid-State Nuclear Magnetic Resonance Spectroscopy
Eugene S. Mananga1,2*, Jalil Moghaddasi1, Ajaz Sana1, Mostafa Sadoqi2
1Physics and Technology Department, BCC, CUNY, New York, USA
2Physics Department, St. John’s University of New York City, New York, USA
Email: *emananga@gc.cuny.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 January 2015; accepted 14 January 2015; published 20 January 2015
ABSTRACT
This short review article presents theories used in solid-state nuclear magnetic resonance spectroscopy. Main theories used in NMR include the average Hamiltonian theory, the Floquet theory and the developing theories are the Fer expansion or the Floquet-Magnus expansion. These approaches provide solutions to the time-dependent Schrodinger equation which is a central problem in quantum physics in general and solid-state nuclear magnetic resonance in particular. Methods of these expansion schemes used as numerical integrators for solving the time dependent Schrodinger equation are presented. The action of their propagator operators is also presented. We highlight potential future theoretical and numerical directions such as the time propagation calculated by Chebychev expansion of the time evolution operators and an interesting transformation called the Cayley method.
Keywords:
Average Hamitonian Theory, Floquet Theory, Fer Expansion, Chebychev Expansion, Caley Transformation

1. Introduction
The Schrodinger equation is the fundamental equation of physics for describing quantum mechanical behavior. In classical physics, the Schrodinger equation predicts the future behavior of a dynamic system and plays an important role of Newton’s laws and conservation of energy [1] . In quantum mechanics, the Schrodinger equation is a partial differential time dependent equation that describes how the quantum state of a physical system changes. The acceptability of Schrodinger equation lies on its applicability in various fields of sciences such as physics, chemistry, and materials science [2] - [6] . For instance in field such as nuclear magnetic resonance (NMR), much effort still needs to be done to explore several problems using the time-dependent Schrodinger equation. These problems include but are not limited to medical imaging, crystallography, ultra short strong laser pulses, biological systems, chemical structures and composition, spin dynamics of superconductors and semiconductors [7] - [26] .
This short review presents some applications of major theories used in NMR spectroscopy such as the average Hamiltonian theory (AHT) and the Floquet theory (FLT), as well as the developing approaches including the Fer expansion (FE) and the Floquet-Magnus expansion (FME) [27] - [36] . We highlight potential future numerical and theoretical directions such as the time propagation operator calculated using Chebychev expansion and the transformation of Cayley [37] - [45] . The wealth of physical problems indicates the importance of having a general method for solving the time evolution of the density operator or the propagator operator in the case of NMR for instance. The density matrix 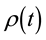 and its antecedent the propagator operator
and its antecedent the propagator operator 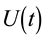 have been extensively used for many-body systems, such as atoms, molecules and nuclei; polarization of light and angular correlation experiments; the theory of masers and maser-like devices; the mean field techniques, such as Hartree-Fock and Thomas-Fermi approximations; the description of atoms and molecules in strong electromagnetic fields; resonance fluorescence and resonance Raman in the presence of intense field. Vast applications are present in electron and nuclear magnetic resonances [6] [46] - [48] . The physical insights provided by the theories presented in this review are illustrated by their applications. The following schematic diagram (Figure 1) shows the Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR [47] .
have been extensively used for many-body systems, such as atoms, molecules and nuclei; polarization of light and angular correlation experiments; the theory of masers and maser-like devices; the mean field techniques, such as Hartree-Fock and Thomas-Fermi approximations; the description of atoms and molecules in strong electromagnetic fields; resonance fluorescence and resonance Raman in the presence of intense field. Vast applications are present in electron and nuclear magnetic resonances [6] [46] - [48] . The physical insights provided by the theories presented in this review are illustrated by their applications. The following schematic diagram (Figure 1) shows the Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR [47] .
Solid-state NMR is a powerful method to elucidate molecular structure and dynamics in systems not amenable to characterization by other methodologies and its importance stands in its ability to accurately determine intermolecular distances and molecular torsion angles [34] [49] - [52] .
Methods developed over the past 3.5 years enabled us to obtain simplified calculations for the common form of Hamiltonian in solid-state NMR and multimode Hamiltonian in its generalized Fourier expansion Hamiltonian [34] . Based on these and other unpublished findings, we now believe that the FME provides a quick and efficient means to calculate higher order terms allowing the disentanglement of the stroboscopic observation and
Figure 1. Flow chart of the evolution operators, theories, foundations, numerical simulations and applications in NMR.
effective Hamiltonian that will be useful to describe spin dynamics processes in solid-state NMR and understand different synchronized or non-synchronized experiments [34] [52] - [55] . Furthermore, our first applications of FE approach to study interactions in solid-state NMR when irradiated with the magic-echo sequence support this goal [52] . The results of the first order 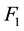 obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian,
obtained for chemical shift, dipolar, and quadrupolar interactions might lead to the average Hamiltonian, 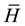 , in the sense of Magnus expansion under the circumstances:
, in the sense of Magnus expansion under the circumstances:
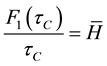 . A salient feature of the Fer and Magnus expansions stem from the fact that, when
. A salient feature of the Fer and Magnus expansions stem from the fact that, when 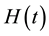 is an
is an
element in a given Lie algebra group, both approaches have the required structure and evolve in the desired group (Lie group). In addition, this is also true for their truncation to any order. We are thus poised to perform more work to ascertain the feasibility of Fer expansion in handling cases involving non-periodic and non-cyclic cases, and to use the expansion schemes of the Magnus (AHT) and the Fer expansions as numerical integrators for solving the time dependent Schrodinger equation which remains the central problem in quantum physics. Theoretical approaches in NMR are challenging, but the potential payoff is substantial, and could ultimately lead not only to a more accurate and efficient spin dynamics simulation, but also to the development of sophisticated RF pulse sequences, and understanding new experiments. Since the first demonstration of nuclear magnetic resonance in condensed matter in 1946 [56] [57] , the field of solid-state NMR has adopted only two milestones theoretical approaches in its history, theories which control the dynamics of spin systems: the average Hamiltonian theory (1968) [27] and the Floquet theory (1982) [30] [31] . However, compared to other spectroscopic techniques, the technique of NMR is well-established and will remain much a vibrant field of research due to its theoretical components driven by mathematicians, chemical and quantum physicists.
The overall goals of this review article is to support theories in NMR in order to continue to a) apply the average Hamiltonian theory to problems including (but not limited to): a class of symmetrical radio-frequency pulse sequences in the NMR of rotating solids, the symmetry principles in the design of NMR multiple-pulse sequences, the composite pulses, and the problems still unsolved such as the AHT for 3 spins [58] - [68] ; b) use the Floquet theory in the study of several magic-angle spinning (MAS) NMR experiments on spin systems with a periodically time-dependent Hamiltonian such as the multiple-multimode Floquet-theory in NMR [69] ; c) enhance the performance of the Floquet-Magnus expansion by considering fundamental questions that arise when dealing with this approach [34] . Using FME method, many interesting problems will be approached such as multi-mode Hamiltonian, rotational-resonance recoupling, continuous wave irradiation on a single species, DARR and MIRROR recoupling, C-type and R-type sequences, TPPM decoupling, etc. [54] [68] [69] ; d) use the Fer expansion to solve similar problems such as those solved using the AHT [32] ; e) explore potential future theoretical and numerical directions for the calculation of the time propagation and evolution operators using Chebychev expansion and Cayley transformation methods [37] [41] - [44] . It is noteworthy that unifying or combining two and more theories known in NMR will continue to provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a more efficient way that can be easily extended to all types of modulations.
2. Average Hamiltonian Theory
Since its first application in NMR in 1968 by Evans, Haeberlen and Waugh, the average Hamiltonian theory has evolved as a powerful technique of analysis in the development of high resolution NMR spectroscopy [27] [70] . The Magnus expansion forms the basis of AHT and has been systematically used in NMR, in particular in solid-state NMR where via AHT the ME has been instrumental in the development of improved techniques in NMR spectroscopy [35] [36] [70] . The approach of AHT is the main tool to control the dynamics of spin systems and to treat theoretical problems in solid-state NMR which have been used sometimes abusively [71] . The basic understanding of AHT involves a time dependent Hamiltonian 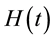 that governs the spin system evolution and describes the effective evolution by an average Hamiltonian
that governs the spin system evolution and describes the effective evolution by an average Hamiltonian 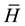 within a periodic time
within a periodic time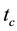 . This is satisfied only if
. This is satisfied only if 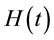 is periodic
is periodic 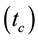 and the observation is stroboscopic and synchronized with period
and the observation is stroboscopic and synchronized with period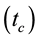 . This technique set the stage for stroboscopic manipulations of spins and spin interactions by radio-frequency pulses and also explains how periodic pulses can be used to transform the symmetry of selected interactions in coupled, many-spin systems considering the average or effective Hamiltonian of the RF pulse train [27] [34] [35] [72] - [75] . Wilhelm Magnus recognizes in his seminal paper of 1954 that his work was stimulated by results on the theory of linear operators in quantum mechanics. This shows that at its early stage, the Magnus expansion was strongly related to physics, and has been ever since then [72] . The central result of AHT is obtained by expressing the evolution propagator
. This technique set the stage for stroboscopic manipulations of spins and spin interactions by radio-frequency pulses and also explains how periodic pulses can be used to transform the symmetry of selected interactions in coupled, many-spin systems considering the average or effective Hamiltonian of the RF pulse train [27] [34] [35] [72] - [75] . Wilhelm Magnus recognizes in his seminal paper of 1954 that his work was stimulated by results on the theory of linear operators in quantum mechanics. This shows that at its early stage, the Magnus expansion was strongly related to physics, and has been ever since then [72] . The central result of AHT is obtained by expressing the evolution propagator 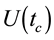 by an average Hamiltonian
by an average Hamiltonian 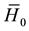 and using the Magnus expansion. The Magnus expansion provides a solution to the initial value problem
and using the Magnus expansion. The Magnus expansion provides a solution to the initial value problem
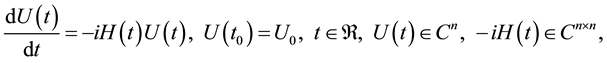 (1)
(1)
in terms of exponentials of combinations of the coefficient matrix

for 


provides 




3. Floquet Theory
The FLT introduced to the NMR community in the early 1980’s simultaneously by Vegaand Maricqis another illuminating and powerful approach that offers a way to describe the time evolution of the spin system at all times and is able to handle multiple incommensurate frequencies [30] [31] [81] [82] . This theory provides a more general approach to AHT and has been applied satisfactorily to study important NMR phenomena [79] [80] [83] . The theory delineates the finite-dimensional time-dependent Liouville space onto an infinite-dimensional but time-independent Floquet space. The general description of the FLT is equally applicable to any nuclear spin systems. However, spin systems with large quadrupolar couplings may violate the convergence conditions for the expansions employed to evaluate the Floquet matrices. An important question to rise is the level of extension the FLT can be used in NMR without losing its conceptual framework. In other words, probing the validity of FLT for quadrupolar nuclei including those with spin I = 1, 3/2, 5/2, and 7/2 by analyzing for example a simple pulse sequence can be beneficial to the NMR community [75] . While the FLT scheme provides a more universal approach for the description of the full time dependence of the response of a periodically time-dependent system, it is most of the time impractical. Analytical calculations are limited to small spin systems and it is difficult to get physical insight from matrix representation. The full Floquet Hamiltonian has an infinite dimension and it is often not very intuitive to understand its implications on the time evolution of the spin system. Matrices for multi-mode Floquet calculations can become intractable. Massive reduction in dimensionality by truncation of the Fourier dimensions can introduce artifacts. In the literature, problems with up to three frequencies have been treated, but the demand of experiments that require four frequencies for a full description is increasing [69] [79] [80] . For instance, non-cyclic multiple-pulse sequences like two-pulse phase-modulated decoupling experiment acquire four frequencies under double rotation and there are some other obvious problems with four frequencies like triple-resonance CW radio frequency irradiation under MAS. Recent articles by Leskes et al., and Scholz et al. discussed extensively several MAS NMR experiments on spin systems with a periodically time-dependent Hamiltonian [69] [79] [80] . For many NMR experiments, understanding the spin dynamics requires a wise choice of the interaction frame in which the Hamiltonian is presented. Ramachandran and Griffin, and Schmidt and Vega introduced remarkable applications of Floquet theory in NMR [82] [83] . Indeed, bases employed in theoretical treatment of FLT and AHT do not extend to multiples spins or I > 1/2 systems, and fails to provide insights in to multiple-quantum NMR phenomena and polarization transfer experiments that involve relaxation. The multipole-multimode Floquet theory (MMFT) presented by Ramachandran and Griffin in its first application still remains a viable alternative for describing both coherent as well as incoherent effects observed in NMR experiments [83] . On one hand, Ramachandran and Griffin combined Shirley’s Floquet approach to the multipole theory proposed by Sanctuary in order toexpand any periodic time-dependent spin Hamiltonian, density operator, and Liouville superoperator in a Fourier series [83] - [85] . Substituting the Fourier expansions of the density operator and the Liouville super-operator in the Liouville equation, the following new set of coupled differential equations spanning an infinite dimensional vector space, with time-independent coefficients were obtained

The notation 
Subsequently, the Floquet density operator and the Hamiltonian operator are represented by


The Floquet Hamiltonian 
operators defined both in the spin 


modulation) with the off-diagonality represented by the indices 


the Floquet transition amplitudes was evaluated to: 



coupled I = 1/2 spin pairs by evaluating two uncoupled homonuclear spins under magic angle sample spinning conditions 






4. Fer Expansion
Analysis and numerical implementation of Magnus expansions is not a trivial task. Therefore, an alternative to the Magnus expansion which is called the Fer expansion can be useful for solving the time-dependent Schrodinger differential equation. This approach was formulated more than half a century ago by Fer and wasrecently introduced to the NMR community by Madhu and Kurur [32] [33] . This expansion is still in its infancy in NMR and can be considered to be complimentary to the Magnus expansion (AHT). Indeed, from the point of view of physical applications, the Magnus expansion has been extensively used in a variety of issues, while the Fer expansion has been either ignored or misquoted until recently [87] . While the efficiency of Fer expansion seems obvious, more effort is still required to allow the approach to overcome difficulties such as cases involving non- periodic and non-cyclic cases. More quantitative work need to be performed in order to bring out the salient features of the Fer expansion and explore its use in solid-state NMR and in many other theoretical areas. The Fer expansion approximates the solution to the initial value problem (Equation (1)) by a product of matrix exponent
tials. The expansion is generated by the recursive scheme, 



The Fer expansion involves a series of nested commutators resulting in




5. Floquet-Magnus Expansion
The Floquet Magnus expansion is a new theoretical tool for describing spin dynamics recently introduced in solid-state NMR and spin physics [34] - [36] . This unique approach (FME) is an extension of the popular Magnus expansion and average Hamiltonian theory and is useful to shed new lights on AHT and FLT [27] [28] . The aims of the FME is to bridge the AHT to the Floquet Theorem but in a more concise and efficient formalism [34] . Calculations can then be performed in a finite-dimensional Hilbert space instead of an infinite dimensional space within the Floquet theory. We expected that the FME will provide means to more accurately and efficiently perform spin dynamics simulation and for devising new RF pulse sequence. We also expect the FME to explore physical implementations of quantum information processing (QIP) and introduce the basic background for understanding applications of NMR in QIP and explain their successes, limitations and potential. The FME provides a quick means to calculate higher order term allowing the disentanglement of the stroboscopic observation 


FLT that could be very useful in simplifying calculations and providing a more intuitive understanding of spin dynamics processes. The approach of FME is essentially distinguished from other theories with its famous function 





the option of a more general representation of the FME with



formal derivation of higher order terms. In the above equations, the 













5.1. Common Form of Hamiltonian in Solid-State NMR
For the sake of simplicity, we considered the Hamiltonian: 
mon form of Hamiltonian in solid-state NMR. 


second rank m-order spherical tensor describing the spin system as defined by 
perturbation theory (SPT) in terms of the irreducible tensor operators gives the diagonal Hamiltonian,

interaction frame where the Hamiltonian becomes time-dependent

is in agreement with the static perturbation theory and Van Vleck transformations. This is not the case of the Magnus expansion. This agreement can be easily explained by the connection that exists between the SPT and
FME propagators written as


5.2. Extension to Multimode Hamiltonian
Considering the generalized Fourier expansion of the Hamiltonian ( 



larly, calculation of second order terms is straightforward [34] .These expressions highlight the fact that the multimode Hamiltonian case can be easily treated in Hilbert space with the FME.
5.3. BABA and C7
For example, applying the first contribution terms of FME to the dipolar Hamiltonian when irradiated with the BABA (Figure 2 and Figure 3) and sevenfold symmetric radiofrequency pulse sequences shown in Figure 3 of
reference [54] , we generated the plots (


the degree of recoupling magnetic dipolar between nuclear spins which is useful for preparing and detecting double quantum coherence [54] [55] [90] . Therefore, the study of the amplitude of DQ terms can be considered as a viable approach for controlling the complex spin dynamics of a spin system evolving under the dipolar in-
teraction of BABA and C7 pulse sequences. The size of 
Figure 2. BABA with delta-pulses.
which indicates the degree of efficiency of the scheme. In reference [54] , a closer look at Figure 4(c) and Figure 5(c) shows that the magnitude of 



serve that all curves are strictly monotonous. This tells us that, the strength of the DQ terms increase continously with time and no decoupling conditions occur in the BABA (with delta-pulse) and C7 pulse sequences.
5.4. BABA with Finite Pulse Width
Now, let us Consider, BABA pulse sequence with finite pulse width where the relation 

only DQ terms in the function

bers 




to BABA with delta-pulse width shows that the magnitude of the DQ terms of BABA with finite pulses is small
compared to the magnitude of BABA with 


Figure 3. BABA with finite pulse width.




magnitude of the double quantum terms decreases, as expected. When
maximum corresponding to the delta-pulse sequence. However, when 


a full decoupling is possible, which occurs at

5.5. Criteria to Average out Chemical Shift Anisotropy for BABA
Application of the first contribution terms of the Floquet-Magnus expansion to the chemical shift anisotropy when irradiated with the BABA pulse sequence lead to an important condition for the CSA to be averaged out in each rotor period 








of the argument of the propagator operator in FME approach was evaluated to

A numerical analysis for a simple case consisting of one spin system with

neous values of the function
molecule and depend on the orientation of the molecule and on the CSA tensor elements. This complex function
can also be ploted versus the dimensionless number 
ferent orientation of the molecule.
6. Potential Approaches and Future Directions
Computing the exponential of a matrix is an important task in quantum mechanics and in nuclear magnetic resonance in particular where all theories used so far rely on exponential Hamiltonian operator propagators. The approximation of the matrix exponential is among the oldest and most extensive research topics in numerical mathematics [35] [39] [92] [93] . Although many efficient algorithms have been developed, so far, the problem is still not having being solved in general. Approaches such as scaling and squaring with Pade approximation, Chebyshev approximation, Krylov space methods, or splitting methods, have been used to approach the exponential of a matrix problem [39] . The main difficulty encountered in spectrum simulation is the rapid increase of computational requirements with an increasing number of spins. Simulation of spin system dynamics requires the numerical solution of the Liouville von Neumann equation, or equivalently the numerical exponential of a Liouville matrix [92] [93] . The Chebyshev approach has the potential to be extensively used in spin quantumdynamics and in particular NMR in the capacity of numerical simulations of spin physics of systems encounters. Our motivation of presenting the Chebyshev approximation as a potential surrogate of the popular expansions in NMR for the task of numerical simulations in spin dynamics paradigm stem from its numerical stability, high accuracy and also because its theoretical advantages are still not entirely realized for currently feasible computations [94] . I addition of the Chebyshev approximation, we introduce another alternative transformation called Cayley method that could be considered in some circumstances.
7. Chebyshev Approach
Nearly three decades ago, Tal-Ezer and Kosloff introduced the Chebyshev method as a means of solving the time-dependent Schrodinger equation in the field of molecular dynamics [37] [92] [94] . Tal-Ezer shown that the complex Chebyshev polynomials achieve the best approximation to expand the evolution operator. In the Chebyshev approach, the evolution operator 



cated Chebyshev expansion of 



advantages: first, it exploits the sparsity of the Liouvillian (Hamiltonian) by expressing the propagator in terms of a sequence of 

8. Cayley Method
The Cayley transform provides a useful alternative to the exponential mapping relating the Lie algebra to the Lie group. This fact is particularly important for numerical methods where the evaluation of the exponential matrix is the most computation-intensive part of the algorithm [35] [97] . Blanes and co-workers shown that the solution
of Equation (1) can be written as 





such that if 




various expansion coefficients. Blanes and co-workers obtained the time-symmetric methods of order 4 and 6, based on the above Cayley transform where the efficiency of Cayley based methods can be built directly from Magnus based integrators [35] . But, unlike Magnus expansions, truncated Cayley expansions do not enjoy the benefits associated with time symmetry. As soon as integrals are replaced by appropriate quadrature formulas, Iserles proved that the time symmetry is gained [41] . The Cayley approach allows employing explicit schemes for solving the differential equation on the Lie algebra of the group and leads to semi-implicit methods where no iteration is required. The Caley methods in the numerical solution of matrix differential systems on quadratic groups have been applied to many important problems such as the Penrose regression problem (PRP) where this approach has been employed in finding numerical solution of PRP, the calculation of Lyapunov exponents of Hamiltonian systems, the solution of Hamiltonian isospectral problems, etc.... [41] -[44] [96] .
9. Conclusions
In this publication, we have thoroughly reviewed the abiding applications of average Hamiltonian theory, Floquet theory, and Floquet-Magnus expansion from very different perpectives in spin quantum physics of nuclear magnetic resonance. We also have presented some potential theories in NMR such as Fer expansion, Chebychev approximation, and possibly Cayley method. The combinations of two or more of the theories therein described will provide a framework for treating time-dependent Hamiltonian in quantum physics and NMR in a way that can be easily extended to both synchronized and several non-synchronized modulations. We hope this publication will encourage the use of Floquet-Magnus and Fer expansions as numerical integrators as well as the use of Floquet-Magnus expansion as alternative approach in designing sophisticated pulse sequences and analyzing and understanding of different experiments. We also hope that this review will contribute to motivate spin dynamics experts in NMR to consider other perspectives and approaches beyond the scope of the current popular or used theories in the field of nuclear magnetic resonance. They are also many remarkable applications of the theory of NMR that we do not discuss in this review such as quantum information processing and computing. For example, the nuclear magnetic resonance quantum calculations of the Jones polynomial are interesting theoretical problems to tackle as well as theoretical treatment of problems with more than three frequencies analyzed using Floquet theory or Floquet-Magnus expansion approaches. In respect with the developments in the mathematical structure of AHT, FLT, FME, and FE, we expect that the realm of applications of the Floquet Magnus expansion and Fer expansion will also wide over the years. With new application in the field of NMR, we also expect the FME to generate new contributions like the generation of efficient numerical algorithm for geometric integrators.
The intention of writing this overview of theories and applications in nuclear magnetic resonance spectroscopy is to help bring the current and future prospective theoretical aspects of spin dynamics in NMR to the attention of the NMR community and lead new interactions between NMR experts and other specialists in mathematics, physics, chemistry, physical chemistry, and chemical physics. All these points strongly support the idea that the Floquet-Magnus expansion, the Fer expansion, the Chebyshev approach, and possibly the Cayley method can also be the very useful and powerful tools in quantum spin dynamics.
Acknowledgements
E. S. Mananga appreciates the moral supports of Profs. Joseph Malinsky, Andrew Akinmoladun and Akhil Lal, Mr. Hamad Khan and Mr. Alfred Romito.
References
- Schrödinger, E. (1926) An Undulatory Theory of the Mechanics of Atoms and Molecules. Physical Review, 28, 1049- 1970. http://dx.doi.org/10.1103/PhysRev.28.1049
- Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, Oxford University Press, Oxford.
- Hazewinkel, M. (2001) Schrodinger Equation. Encyclopedia of Mathematics, Edition Springer.
- Müller-Kirsten, H.J.W. (2012) Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral. 2nd Edition, World Scientific. http://dx.doi.org/10.1142/8428
- Griffiths, D.J. (2004) Introduction to Quantum Mechanics. 2nd Edition, Benjamin Cummings.
- Berman, M. and Kosloff, R. (1991) Time-Dependent Solution of the Liouville-Von Neumann Equation: Non-Dissipa- tive Evolution. Computer Physics Communications, 63, 1-20. http://dx.doi.org/10.1016/0010-4655(91)90233-B
- Andrew, E.R., Bradbury, A. and Eades, R.G. (1958) Nuclear Magnetic Resonance Spectra from a Crystal Rotated at High Speed. Nature, 182, 1659. http://dx.doi.org/10.1038/1821659a0
- Andrew, E.R., Bradbury, A. and Eades, R.G. (1959) Removal of Dipolar Broadening of Nuclear Magnetic Resonance Spectra of Solids by Specimen Rotation. Nature, 183, 1802-1803. http://dx.doi.org/10.1038/1831802a0
- Lowe, I.J. (1959) Free Induction Decays of Rotating Solids. Physical Review Letters, 2, 285-287. http://dx.doi.org/10.1103/PhysRevLett.2.285
- Schaefer, J. and Stejskal, E.O. (1976) Carbon-13 Nuclear Magnetic Resonance of Polymers Spinning at the Magic Angle. Journal of American Chemical Society, 98, 1031. http://dx.doi.org/10.1021/ja00420a036
- Ernst, R.R., Bodenhausen, G. and Wokaun, A. (1987) Principles of Nuclear Magnetic Resonance in One and Two Dimensions. Clarendon, Oxford.
- Hafner, S. and Demco, D.E. (2002) Solid-State NMR Spectroscopy under Periodic Modulation by Fast Magic Angle Spinning and Pulses: A Review. Solid State Nuclear Magnetic Resonance, 22, 247-274.
- Mehring, M., Pines, A., Rhim, W.-K. and Waugh, J.S. (1971) Spin-Decoupling in the Resolution of Chemical Shifts in Solids by Pulsed NMR. Journal of Chemical Physics, 54, 3239-3240. http://dx.doi.org/10.1006/snmr.2002.0088
- Jaroniec, C.P., Tounge, B.A., Rienstra, C.M., Herzfeld, J. and Griffin, R.G. (2000) Recoupling of Heteronuclear Dipolar Interactions with Rotational-Echo Double-Resonance at High Magic-Angle Spinning Frequencies. Journal of Magnetic Resonance, 146, 132-139. http://dx.doi.org/10.1006/jmre.2000.2128
- Charpentier, T., Fermon, C. and Virlet, J. (1998) Efficient Time Propagation Technique for MAS NMR Simulation: Application to Quadrupolar Nuclei. Journal of Magnetic Resonance, 132, 181-190. http://dx.doi.org/10.1006/jmre.1998.1415
- Ernst, M., Geen, H. and Meier, B.H. (2006) Amplitude-Modulated Decoupling in Rotating Solids: A Bimodal Floquet Approach. Solid State Nucleaire Magnetic Resonance, 29, 2-21. http://dx.doi.org/10.1016/j.ssnmr.2005.08.004
- Barone, S.R., Narcowich, M.A. and Narcowich, F.J. (1977) Floquet Theory and Applications. Physical Review A, 15, 1109-1125. http://dx.doi.org/10.1103/PhysRevA.15.1109
- Filip, C., Filip, X., Demco, D.E. and Hafner, S. (1997) Spin Dynamics under Magic Angle Spinning by Floquet Formalism. Molecular Physics, 92, 757-771. http://dx.doi.org/10.1080/002689797170031
- Friedrich, U., Schnell, I., Brown, S.P., Lupulescu, A., Demco, D.E. and Spiess, H.W. (1998) Spinning-Sideband Patterns in Multiple-Quantum Magic-Angle Spinning NMR Spectroscopy. Molecular Physics, 95, 1209-1227. http://dx.doi.org/10.1080/00268979809483252
- Boender, G.J., Vega, S. and De Groot, H.J.M. (2000) Quantized Field Description of Rotor Frequency-Driven Dipolar Recoupling. Journal of Chemical Physics, 112, 1096-1106. http://dx.doi.org/10.1063/1.480664
- Ernst, M., Samoson, A. and Meier, B.H. (2005) Decoupling and Recoupling Using Continuous Waves Irradiation in Magic-Angle-Spinning Solid-State NMR: A Unified Description Using Bimodal Floquet Theory. Journal of Chemical Physics, 123, Article ID: 064102. http://dx.doi.org/10.1063/1.1944291
- Ding, S. and McDowell, C.A. (1998) The Equivalence between Floquet Formalism and the Multi-Step Approach in Computing the Evolution Operator of a Periodical Time-Dependent Hamiltonian. Chemical Physics Letters, 288, 230- 234. http://dx.doi.org/10.1016/S0009-2614(98)00307-8
- Buishvili, L.L., Volzhan, E.B. and Menabde, M.G. (1981) Higher Approximations in the Theory of the Average Hamiltonian. Theoretical and Mathematical Physics, 46, 166-173. http://dx.doi.org/10.1007/BF01030852
- Emetere, M.E. (2014) Analytical Solutions of Three Dimensional Time-Dependent Shrodinger Equation Using Bloch NMR Approach for NMR Studies. Applied Mathematical Sciences, 8, 2753-2762. http://dx.doi.org/10.12988/ams.2014.4012
- Lee, Y.K., Kurur, N.D., Helmle, M., Johannessen, O.G., Nielsen, N.C. and Levitt, M.H. (1995) Efficient Dipolar Recoupling in the NMR of Rotating Solids. A Sevenfold Symmetric Radiofrequency Pulse Sequence. Chemical Physical Letters, 242, 304-309. http://dx.doi.org/10.1016/0009-2614(95)00741-L
- Leforestier, C., Bisseling, R.H., Cerjan, C., Feit, M.D., Friesner, R., Guldberg, A., Hammerich, A., Jolicard, G., Karrlein, W., Meyer, H.-D., Lipkin, N., Roncero, O. and Kosloff, R. (1991) A Comparison of Different Propagation Schemes for the Time Dependent Schrödinger Equation. Journal of Computational Physics, 94, 59-80. http://dx.doi.org/10.1016/0021-9991(91)90137-A
- Haeberlen, U. and Waugh, J.S. (1968) Coherent Averaging Effects in Magnetic Resonance. Physical Review, 175, 453- 467. http://dx.doi.org/10.1103/PhysRev.175.453
- Floquet, G. (1883) Sur les Equations Differentielles Lineaires a Coefficients Periodiques. Annales Scientifics de l’Ecole Normale Superieur, 12, 47-88. http://eudml.org/doc/80895
- Shirley, J.H. (1965) Solution of the Schrödinger Equation with a Hamiltonian Periodic in Time. Physical Review, 138, B979-B987. http://dx.doi.org/10.1103/PhysRev.138.B979
- Maricq, M.M. (1982) Application of Average Hamiltonian Theory to the NMR of Solids. Physical Review B25, 6622-6632. http://dx.doi.org/10.1103/PhysRevB.25.6622
- Zur, Y., Levitt, M.H. and Vega, S. (1983) Multiphoton NMR Spectroscopy on a Spin System with I=1/2. Journal of Chemical Physics, 78, 5293. http://dx.doi.org/10.1063/1.445483
- Madhu, P.K. and Kurur, N.D. (2006) Fer Expansion for Effective Propagators and Hamiltonians in NMR. Chemical Physical Letters, 418, 235-238. http://dx.doi.org/10.1016/j.cplett.2005.10.134
- Fer, F. (1958) Bulletin de la Classe des Sciences. Academie Royalede Belgique, 44, 818-829.
- Mananga, E.S. and Charpentier, T. (2011) Introduction of the Floquet-Magnus Expansion in Solid-State Nuclear Magnetic Resonance Spectroscopy. Journal of Chemical Physics, 135, Article ID: 044109. http://dx.doi.org/10.1063/1.3610943
- Blanes, S., Casas, F., Oteo, J.A. and Ros, J. (2009) The Magnus Expansion and Some of Its Applications. Physics Reports, 470, 151-238. http://dx.doi.org/10.1016/j.physrep.2008.11.001
- Casas, F., Oteo, J.A. and Ros, J. (2001) Floquet Theory: Exponential Perturbative Treatment. Journal of Physics A: Mathematical and General, 34, 3379-3388. http://dx.doi.org/10.1088/0305-4470/34/16/305
- Dumont, R.S., Jain, S. and Bain, A. (1997) Simulation of Many-Spin System Dynamics via Sparse Matrix Methodology. Journal of Chemical Physics, 106, 5928. http://dx.doi.org/10.1063/1.473258
- Scholz, I., Meier, B.H. and Ernst, M. (2007) Operator-Based Triple-Mode Floquet Theory in Solid-State NMR. Journal of Chemical Physics, 127, Article ID: 204504. http://dx.doi.org/10.1063/1.2800319
- Süli, E. and Mayers, D. (2003) An Introduction to Numerical Analysis. Cambridge University Press, Cambridge.
- Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions. Dover Publications, Dover.
- Iserles, A. (2001) On Cayley-Transform Methods for the Discretization of Lie-Group Equations. Foundations on Computational Mathematics, 1, 129-160. http://dx.doi.org/10.1007/s102080010003
- Chu, M.T. and Morris, L.K. (1988) Isospectral Flows and Abstract Matrix Factorization. Society for Industrial and Applied Mathematics Journal of Numerical Analysis, 25, 1383-1391. http://dx.doi.org/10.1137/0725080
- Leimkuhler, J.B. and Van Vleck, E.S. (1997) Orthosymplectic Integration of Linear Hamiltonian System. Numerical Mathematics, 77, 269-282. http://dx.doi.org/10.1007/s002110050286
- Lewis, D. and Simo, J.C. (1994) Conserving Algorithms for the Dynamics of Hamiltonian Systems on Lie Groups. Journal of Nonlinear Science, 4, 253-299. http://dx.doi.org/10.1007/BF02430634
- Abragam, A. (1961) The Principle of Nuclear Magnetism. Clarendon Press, Oxford.
- Ben-Reuven, A. and Rabin, Y. (1979) Theory of Resonance Scattering and Absorption of Strong Coherent Radiation by Thermally Relaxing Multi-Level Atomic Systems. Physical Review A, 19, 2056-2073. http://dx.doi.org/10.1103/PhysRevA.19.2056
- Mananga, E.S. (2014) Future Theoretical Approaches in Nuclear Magnetic Resonance. Journal of Modern Physics, 5, 145-148.
- Raleigh, D.P., Levitt, M.H. and Griffin, R.G. (1988) Rotational Resonance in Solid State NMR. Chemical Physics Letters, 146, 71-76. http://dx.doi.org/10.1016/0009-2614(88)85051-6
- Hohwy, M., Rienstra, C.M., Jaroniec, C.P. and Griffin, R.G. (1999) Fivefold Symmetric Homonuclear Dipolar Recoupling in Rotating Solids: Application to Double Quantum Spectroscopy. Journal of Chemical Physics, 110, 7983. http://dx.doi.org/10.1063/1.478702
- Ishii, Y., Terao, T. and Kainosho, M. (1996) Relayed Anisotropy Correlation NMR: Determination of Dihedral Angles in Solids. Chemical Physics Letters, 265, 133-140. http://dx.doi.org/10.1016/0009-2614(96)00426-5
- Ishii, Y., Hirao, K., Terao, T., Terauchi, T., Oba, M., Nishiyama, K. and Kainosho, M. (1998) Determination of Peptide Angles in Solids by Relayed Anisotropy Correlation NMR. Solid State Nuclear Magnetic Resonance, 11, 169- 175. http://dx.doi.org/10.1016/S0926-2040(98)00038-1
- Mananga, E.S. (2013) Applications of Floquet-Magnus Expansion, Average Hamiltonian Theory and Fer Expansion to Study Interactions in Solid State NMR When Irradiated with the Magic-Echo Sequence. Solid State Nuclear Magnetic Resonance, 55-56, 54-62. http://dx.doi.org/10.1016/j.ssnmr.2013.08.002
- Mananga, E.S. (2013) Criteria to Average Out the Chemical Shift Anisotropy in Solid-State NMR When Irradiated with BABA I, BABA II, and C7 Radiofrequency Pulse Sequences. Solid State Nuclear Magnetic Resonance, 55-56, 63-72. http://dx.doi.org/10.1016/j.ssnmr.2013.08.003
- Mananga, E.S., Reid, A.E. and Charpentier, T. (2012) Efficient Theory of Dipolar Recoupling in Solid-State Nuclear Magnetic Resonance of Rotating Solids using Floquet-Magnus Expansion: Application on BABA and C7 Radiofrequency Pulse Sequences. Solid State Nuclear Magnetic Resonance, 41, 32-47. http://dx.doi.org/10.1016/j.ssnmr.2011.11.004
- Mananga, E.S. and Reid, A.E. (2013) Investigation of the Effect of Finite Pulse Errors on the BABA Pulse Sequence using the Floquet-Magnus Expansion Approach. Molecular Physics, 111, 243-257. http://dx.doi.org/10.1080/00268976.2012.718379
- Purcell, E.M., Torrey, H.C. and Pound, R.V. (1946) Resonance Absorption by Nuclear Magnetic Moments in a Solid. Physical Review, 69, 37-38. http://dx.doi.org/10.1103/PhysRev.69.37
- Bloch, F., Hansen, W.W. and Packard, M. (1946) The Nuclear Induction Experiment. Physical Review, 70, 474-485. http://dx.doi.org/10.1103/PhysRev.70.474
- Brinkmann, A., Eden, M. and Levitt, M.H. (2000) Synchronous Helical Pulse Sequences in Magic-Angle Spinning Nuclear Magnetic Resonance: Double Quantum Recoupling of Multiple-Spin Systems. Journal of Chemical Physics, 112, 8539. http://dx.doi.org/10.1063/1.481458
- Hohwy, M., Jakobsen, H.J., Eden, M., Levitt, M.H. and Nielsen, N.C. (1998) Broadband Dipolar Recoupling in the Nuclear Magnetic Resonance of Rotating Solids: A Compensated C7 Pulse Sequence. Journal of Chemical Physics, 108, 2686. http://dx.doi.org/10.1063/1.475661
- Brinkmann, A. and Levitt, M.H. (2001) Symmetry Principles in the Nuclear Magnetic Resonance of Spinning Solids: Heteronuclear Recoupling by Generalized Hatmann-Hahn Sequences. Journal of Chemical Physics, 115, 357. http://dx.doi.org/10.1063/1.1377031
- Carravetta, M., Eden, M., Zhao, X., Brinkmann, A. and Levitt, M.H. (2000) Symmetry Principles for the Design of Radiofrequency Pulse Sequences in the Nuclear Magnetic Resonance of Rotating Solids. Chemical Physical Letters, 321, 205-215. http://dx.doi.org/10.1016/S0009-2614(00)00340-7
- Tycko, R. (2007) Symmetry-Based Constant-Time Homonuclear Dipolar Recoupling in Solid-State NMR. Journal of Chemical Physics, 126, Article ID: 064506. http://dx.doi.org/10.1063/1.2437194
- Tycko, R. (2008) Lecture Notes for the First Winter School on Biomolecular Solid State NMR, Stowe, Vermont, 20-25 January 2008.
- Eden, M. and Levitt, M.H. (1999) Pulse Sequence Symmetries in Nuclear Magnetic Resonance of Spinning Solids: Application to Heteronuclear Decoupling. Journal of Chemical Physics, 111, 1511. http://dx.doi.org/10.1063/1.479410
- Sanctuary, B.C. and Cole, H.B.R. (1987) Multipole Theory of Composite Pulses. Journal of Magnetic Resonance, 71, 106-115. http://dx.doi.org/10.1016/0022-2364(87)90131-4
- Levitt, M.H. (1982) Symmetrical Composite Pulse Sequences for NMR Population Inversion. I. Compensation of Radiofrequency Field Inhomogeneity. Journal of Magnetic Resonance, 48, 234-264. http://dx.doi.org/10.1016/0022-2364(82)90275-X
- Tycko, R., Cho, H.M., Schneider, E. and Pines, A. (1985) Composite Pulses without Phase Distortion. Journal of Magnetic Resonance, 61, 90-101. http://dx.doi.org/10.1016/0022-2364(85)90270-7
- Leskes, M., Madhu, P.K. and Vega, S. (2010) Floquet Theory in Solid-State Nuclear Magnetic Resonance. Progress in Nuclear Magnetic Resonance Spectroscopy, 55, 345-380. http://dx.doi.org/10.1016/j.pnmrs.2010.06.002
- Scholz, I., Van Beek, J.D. and Ernst, M. (2010) Operator-Based Floquet Theory in Solid-State NMR. Solid State Nuclear Magnetic Resonance, 37, 39-59. http://dx.doi.org/10.1016/j.ssnmr.2010.04.003
- Evans, W. (1968) On Some Applications of Magnus Expansion in Nuclear Magnetic Resonance. Annals of Physics, 48, 72-93. http://dx.doi.org/10.1016/0003-4916(68)90270-4
- Goldman, M., Grandinetti, P.J., Llor, A., Olejniczak, Z., Sachleben, J.R. and Zwanziger, J.W. (1992) Theoretical Aspects of Higher-Order Truncations in Solid-State Nuclear Magnetic Resonance. Journal of Chemical Physics, 97, 8947. http://dx.doi.org/10.1063/1.463321
- Tycko, R. (2008) Introduction to Special Topic: New Developments in Magnetic Resonance. Journal of Chemical Physical, 128, Article ID: 052101. http://dx.doi.org/10.1063/1.2833958
- Mananga, E.S., Roopchand, R., Rumala, Y.S. and Boutis, G.S. (2007) On the Application of Magic Echo Cycles for Quadrupolar Echo Spectroscopy of Spin-1 Nuclei. Journal of Magnetic Resonance, 185, 28-37. http://dx.doi.org/10.1016/j.jmr.2006.10.016
- Mananga, E.S., Rumala, Y.S. and Boutis, G.S. (2006) Finite Pulse Width Artifact Suppression in Spin-1 Quadrupolar Echo Spectra by Phase Cycling. Journal of Magnetic Resonance, 181, 296-303. http://dx.doi.org/10.1016/j.jmr.2006.05.015
- Mananga, E.S., Hsu, C.D., Ishmael, S., Islam, T. and Boutis, G.S. (2008) Probing the Validity of Average Hamiltonian Theory for Spin I=1, 3/2 and 5/2 Nuclei by Analyzing a Simple Two-Pulse Sequence. Journal of Magnetic Resonance, 193, 10-22. http://dx.doi.org/10.1016/j.jmr.2008.03.014
- Levitt, M.H. (2008) Symmetry in the Design of NMR Multiple-Pulse Sequences. Journal of Chemical Physics, 128, Article ID: 052205. http://dx.doi.org/10.1063/1.2833958
- Vandersypen, L.M.K. and Chuang, I.L. (2004) NMR Techniques for Quantum Control and Computation. Review of Modern Physics, 76, 1037-1069. http://dx.doi.org/10.1103/RevModPhys.76.1037
- Hu, B., Delevoye, L., Lafon, O., Trebosc, J. and Amoureux, J.P. (2009) Double-Quantum NMR Spectroscopy of 31P Species Submitted to Very Large CSAs. Journal of MagneticResonance, 200, 178-188. http://dx.doi.org/10.1016/j.jmr.2009.06.020
- Scholz, I., Van Beek, J.D. and Ernst, M. (2010) Operator-Based Floquet Theory in Solid-State NMR. Solid State Nuclear Magnetic Resonance, 37, 39-59. http://dx.doi.org/10.1016/j.ssnmr.2010.04.003
- Leskes, M., Akbey, U., Oschkinat, H., van Rossum, B.-J. and Vega, S. (2011) Radio Frequency Assisted Homonuclear Recoupling―A Floquet Description of Homonuclear Recoupling via Surrounding Heteronuclei in Fully Protonated to Fully Deuterated Systems. Journal of Magnetic Resonance, 209, 207-219. http://dx.doi.org/10.1016/j.jmr.2011.01.015
- Mehring, M. (1983) Principles of High Resolution NMR in Solids. Springer-Verlag, New York.
- Schmidt-Rohr, K. and Spiess, H.W. (1996) Multidimensional Solid-State NMR and Polymers. Academic Press, London.
- Schmidt, A. and Vega, S. (1992) The Floquet Theory of Nuclear Magnetic Resonance Spectroscopy of Single Spins and Dipolar Coupled Spin Pairs in Rotating Solids. Journal of Chemical Physics, 96, 2655. http://dx.doi.org/10.1063/1.462015
- Ramachandran, R. and Griffin, R.G. (2005) Multipole-Multimode Floquet Theory in Nuclear Magnetic Resonance. Journal of Chemical Physics, 122, Article ID: 164502. http://dx.doi.org/10.1063/1.1875092
- Sanctuary, B.C. (1976) Multipole Operators for an Arbitrary Number of Spins. Journal of Chemical Physics, 64, 4352. http://dx.doi.org/10.1063/1.432104
- Sanctuary, B.C. (1983) Multipole NMR. Molecular Physics, 48, 1155-1176. http://dx.doi.org/10.1080/00268978300100841
- Ramesh, R. and Krishnan, M.S. (2001) Effective Hamiltonians in Floquet Theory of Magic Angle Spinning Using van Vleck Transformation. Journal of Chemical Physics, 114, 5967. http://dx.doi.org/10.1063/1.1354147
- Blanes, S., Casas, F., Oteo, J.A. and Ros, J. (1998) Magnus and Fer Expansions for Matrix Differential Equations: The Convergence Problem. Journal of Physics A: Mathematical and General, 31, 259-268. http://dx.doi.org/10.1088/0305-4470/31/1/023
- Haeberlen, U. (1976) Advance in Magnetic Resonance. Supplement 1, Academic Press, New York.
- Casa, F., Oteo, J.A. and Ros, J. (1991) Lie Algebraic Approach to Fer’s Expansion for Classical Hamiltonian Systems. Journal of Physics A: Mathematical and General, 24, 4037-4046. http://dx.doi.org/10.1088/0305-4470/24/17/020
- Feike, M., Demco, D.E., Graf, R., Gottwald, J., Hafner, S. and Spiess, H.W. (1996) Broadband Multiple-Quantum NMR Spectroscopy. Journal of Magnetic Resonance A, 122, 214-221. http://dx.doi.org/10.1006/jmra.1996.0197
- Mananga, E.S. (2013) Progress in Spin Dynamics Solid-State Nuclear Magnetic Resonance with the Application of Floquet-Magnus Expansion to Chemical Shift Anisotropy. Solid State Nuclear Magnetic Resonance, 54, 1-7. http://dx.doi.org/10.1016/j.ssnmr.2013.04.001
- Tal-Ezer, H. and Kosloff, R. (1984) An Accurate and Efficient Scheme for Propagating the Time Dependent Schrödinger Equation. Journal of Chemical Physics, 81, 3967. http://dx.doi.org/10.1063/1.448136
- Moler, C.B. and Van Loan, C.F. (2003) Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later. Society for Industrial and Applied Mathematics Review, 45, 3-49. http://dx.doi.org/10.1137/S00361445024180
- Rivlin, T.J. (1990) Chebychev Polynomials. 2nd Edition, Wiley, New York.
- Blanes, S., Casas, F. and Ros, J. (2002) High Order Optimized Geometric Integrators for Linear Differential Equations. BIT, 42, 262-284.
- Lopez, L. and Politi, T. (2001) Applications of the Cayley Approach in the Numerical Solution of Matrix Differential Systems on Quadratic Groups. Applied Numerical Mathematics, 36, 35-55. http://dx.doi.org/10.1016/S0168-9274(99)00049-5
NOTES
*Corresponding author.





