World Journal of Nuclear Science and Technology
Vol.2 No.4(2012), Article ID:23771,6 pages DOI:10.4236/wjnst.2012.24021
An Approximation for the Doppler Broadening Function and Interference Term Using Fourier Series
1Department Nuclear Engineering, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
2Brazilian Nuclear Energy Commission, Rio de Janeiro, Brazil
Email: alessandro@nuclear.ufrj.br
Received June 18, 2012; revised July 20, 2012; accepted July 31, 2012
Keywords: Doppler Broadening Function; Fourier Series; New Formulation for the Interference
ABSTRACT
The calculation of the Doppler broadening function  and of the interference term
and of the interference term  are important in the generation of nuclear data. In a recent paper, Goncalves and Martinez proposed an analytical approximation for the calculation of both functions based in sine and cosine Fourier transforms. This paper presents new approximations for these functions,
are important in the generation of nuclear data. In a recent paper, Goncalves and Martinez proposed an analytical approximation for the calculation of both functions based in sine and cosine Fourier transforms. This paper presents new approximations for these functions,  and
and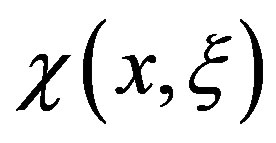 , using expansions in Fourier series, generating expressions that are simple, fast and precise. Numerical tests applied to the calculation of scattering average cross section provided satisfactory accuracy.
, using expansions in Fourier series, generating expressions that are simple, fast and precise. Numerical tests applied to the calculation of scattering average cross section provided satisfactory accuracy.
1. Introduction
The phenomenon of thermal motion of the nuclei inside a nuclear reactor is well represented by the microscopic cross section of the neutron-nucleus interaction through the effect Doppler broadening. The precise determination of the Doppler broadening function and interference term are important for the calculation of the resonance integrals [1,2], self-shielding factors and for corrections of the measurements of the microscopic cross sections with the use of the activation technique [3].
The evaluation of the Doppler broadening function 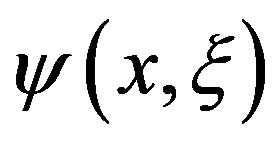 and of the interference term
and of the interference term 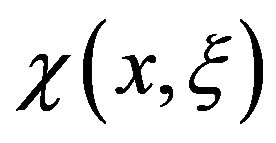 have a great importance in the generation of nuclear data and there are several methods for the calculation of both functions. This paper presents a new approximation for interference term applied to the calculation scattering average cross section [4] using expansions in Fourier series. The results have shown satisfactory accuracy and do not depend on the type of resonance considered. In thermally balanced medium at temperature T the velocity of the target nucleus is distributed by the Maxwell-Boltzmann distribution [5] and the expression for the average scattering cross sections is written, using to the one level formalism of Briet-Wigner, as:
have a great importance in the generation of nuclear data and there are several methods for the calculation of both functions. This paper presents a new approximation for interference term applied to the calculation scattering average cross section [4] using expansions in Fourier series. The results have shown satisfactory accuracy and do not depend on the type of resonance considered. In thermally balanced medium at temperature T the velocity of the target nucleus is distributed by the Maxwell-Boltzmann distribution [5] and the expression for the average scattering cross sections is written, using to the one level formalism of Briet-Wigner, as:
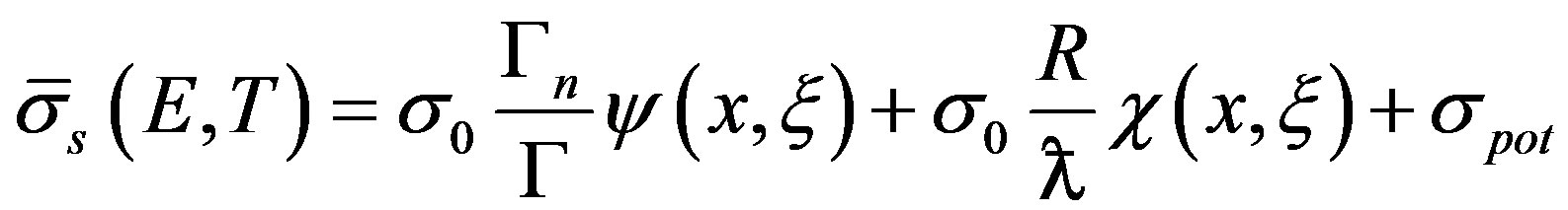 (1)
(1)
where, the interference term and the Doppler broadening function are written, according with approximations proposed by Gonçalves et al. [6], by:
 (2)
(2)
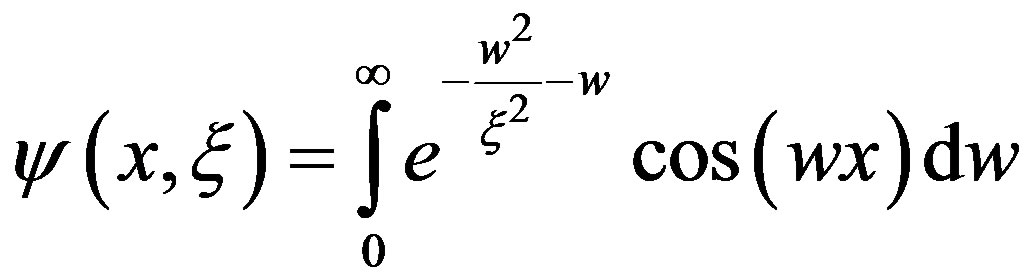 (3)
(3)
The equations (2) and (3) can be interpreted as sine and cosine Fourier transforms.
2. Mathematical Formulation
The integrals expressed by Equations (2) and (3) it is possible to find new representations for functions 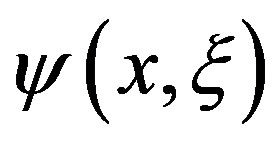 and
and  using the Fourier series technique. In order to turn its use easily, Equations (2) and (3) can be re-written as:
using the Fourier series technique. In order to turn its use easily, Equations (2) and (3) can be re-written as:
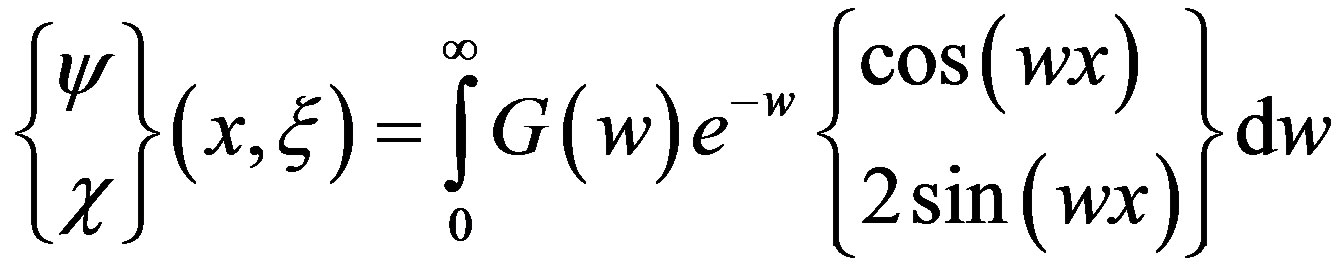 (4)
(4)
where,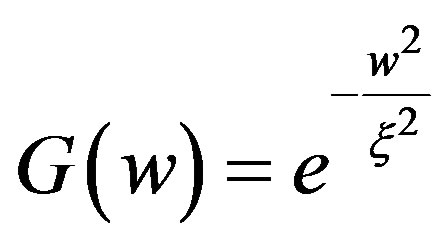 .
.
Analyzing the function 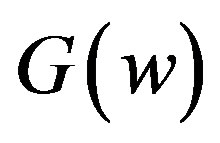 can be observed that it is a continuous and even function, which ensures it has a Fourier series representation. Thus, its Fourier series representation is given by:
can be observed that it is a continuous and even function, which ensures it has a Fourier series representation. Thus, its Fourier series representation is given by:
 (5)
(5)
where
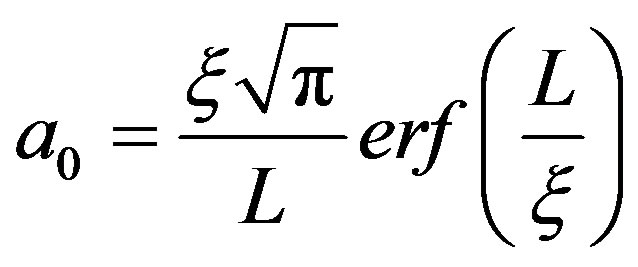 (6)
(6)
 (7)
(7)
Replacing the Equation (5) in the Equation (4) and applying the properties of the error functions with an imaginary argument [7], one can write the following expression for the functions 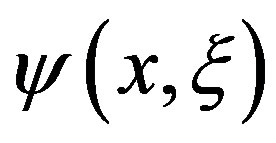 and
and :
:
 (8)
(8)
 (9)
(9)
where,
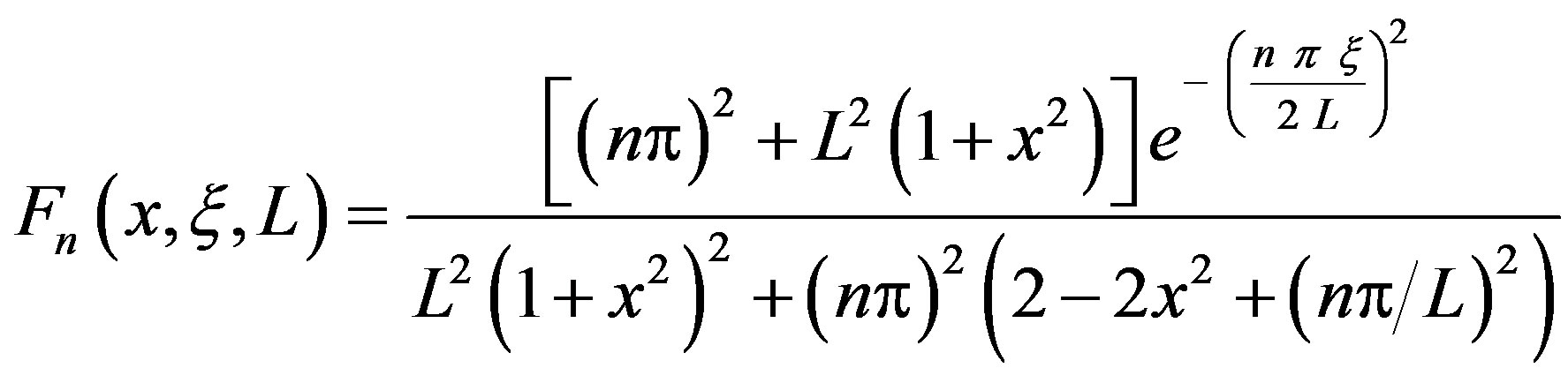 (10)
(10)
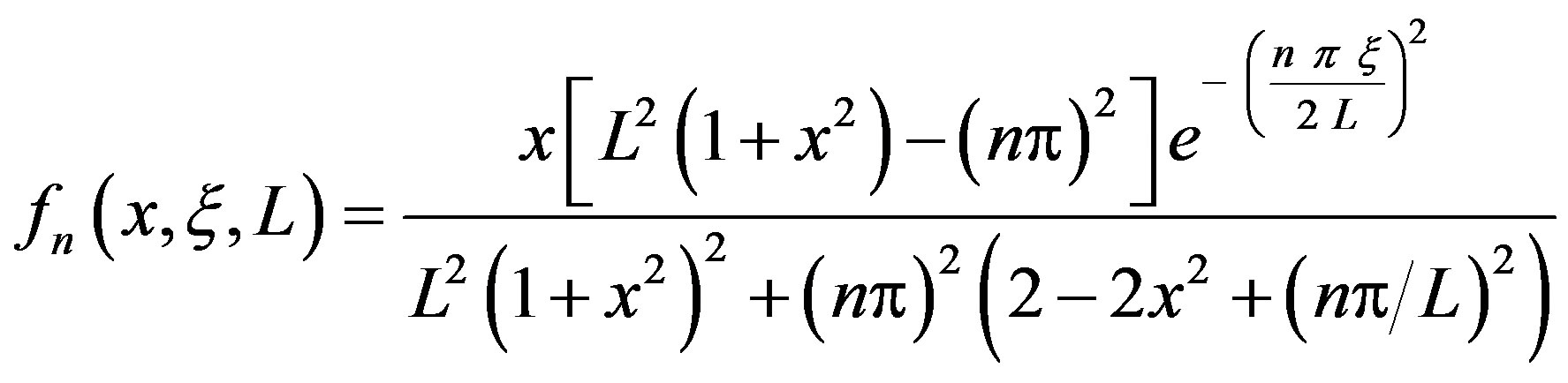 (11)
(11)
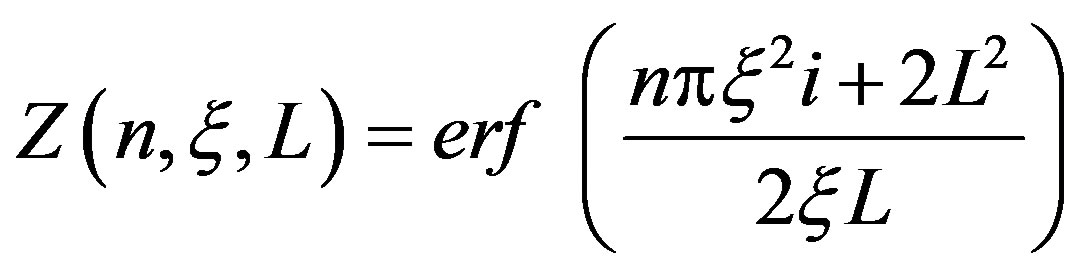 (12)
(12)
Replacing Equations (8) and (9) in Equation (1) one obtains the following expression for the average scattering cross section:
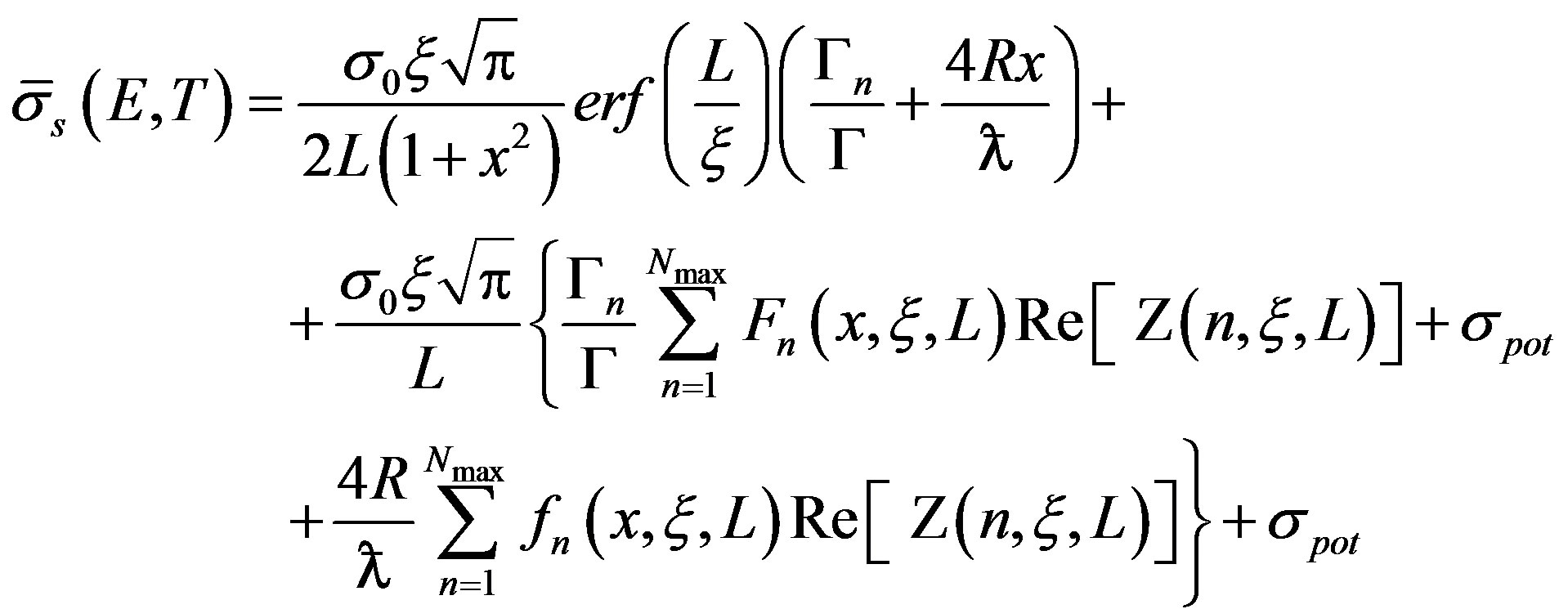 (13)
(13)
3. Numerical Test
This section contains the results obtained with Equations (8) and (9) for the calculation interference term and of the Doppler broadening function with L = π and Nmax = 50. In order to validate the obtained expression in this paper for 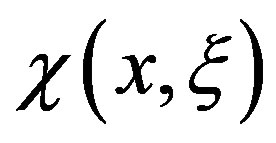 and
and , a systematic compareson was carried out with the comparison between the method presented in this paper and the 4-pole Padé approximation method, whose functional form is:
, a systematic compareson was carried out with the comparison between the method presented in this paper and the 4-pole Padé approximation method, whose functional form is:
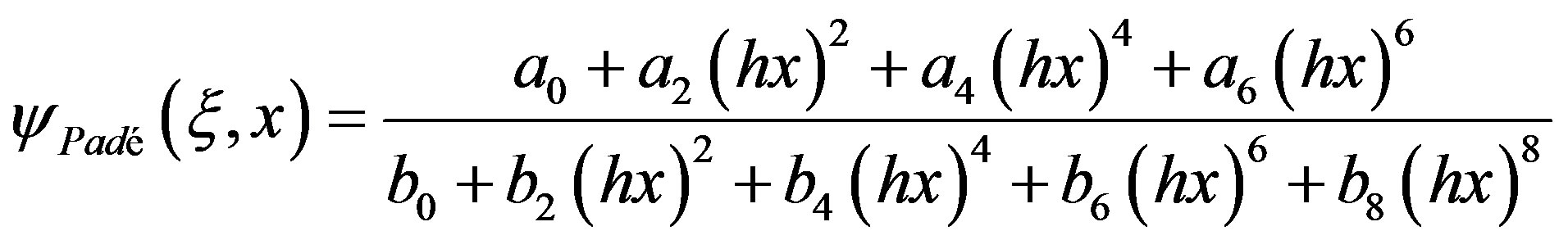 (14)
(14)
 (15)
(15)
The coefficients in Equations (14) and (15) are given by [8,9].
Figures 1 to 8 show the relative errors for the calculation of  and
and , using the proposed method paper, Equations (8) and (9), and the 4-pole Padé method, Equations (14) and (15), considering the benchmark results from Gauss-Legendre quadrature method that is well described in the literature [10].
, using the proposed method paper, Equations (8) and (9), and the 4-pole Padé method, Equations (14) and (15), considering the benchmark results from Gauss-Legendre quadrature method that is well described in the literature [10].
From the Figures 1 and 2 is possible to see that when the variable ξ increases, keeping the variable x constant, the relative deviations of the Padé approximation increases and are systematically higher than those of the proposed method, Equation (8), in the calculation of the function .
.
From the Figures 3 and 4 it is possible to see that when the variable x increases, keeping the variable ξ constant, the relative deviations of the Padé approximation increases and are systematically higher than those of the proposed method, Equation (8), in the calculation of the function .
.

Figure 1. Relative error for the 4-pole Padé approximation, Equation (14), and for the proposed method, Equation (8), for x = 20.

Figure 2. Relative error for the 4-pole Padé approximation, Equation (14), and for the proposed method, Equation (8), for x = 35.

Figure 3. Relative error for the 4-pole Padé approximation, Equation (14), and for the proposed method, Equation (8), for ξ = 0.10.
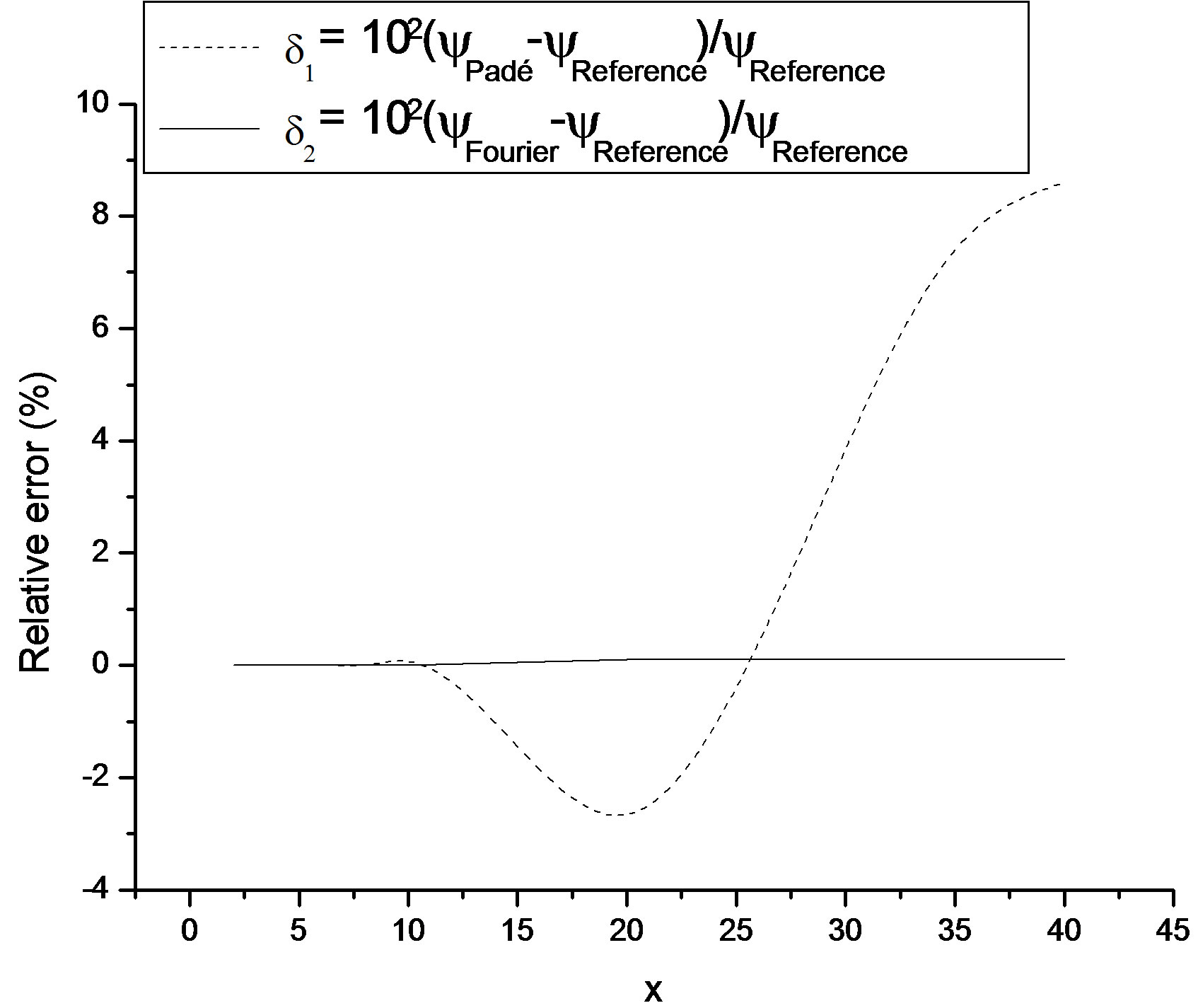
Figure 4. Relative error for the 4-pole Padé approximation, Equation (14), and for the proposed method, Equation (8), for ξ = 0.20.

Figure 5. Relative error for the 4-pole Padé approximation, Equation (15), and for the proposed method, Equation (9), for x = 20.

Figure 6. Relative error for the 4-pole Padé approximation, Equation (15), and for the proposed method, Equation (9), for x = 35.
From the Figures 5 and 6 it is possible to see that when the variable ξ increases, keeping the variable x constant, the relative deviations of the Padé approximation increases and are systematically higher than those of the proposed method, Equation (8), in the calculation of the function .
.
From the Figures 7 and 8 it is possible to see that when the variable x increases, keeping the variable ξ constant, the relative deviations of the Padé approximation increases and are systematically higher than those of the proposed method, Equation (8), in the calculation of the function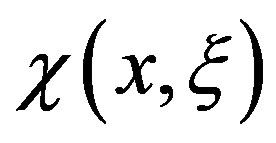 .
.

Figure 7. Relative error for the 4-pole Padé approximation, Equation (15), and for the proposed method, Equation (9), for ξ = 0.15.

Figure 8. Relative error for the 4-pole Padé approximation, Equation (15), and for the proposed method, Equation (9), for ξ = 0.25.
The analysis of the results showed in Figures 1-8 lead to the conclusion that the proposed method proved to be very precise and stable, having a 0.1% maximum relative error margin, when compared to reference values. From these results is possible to apply the approximate formalism presented in this paper in the calculation of the Doppler broadening function  and the Interference Term
and the Interference Term 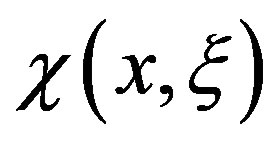 in the determination of the microscopic average scattering cross sections.
in the determination of the microscopic average scattering cross sections.
4. Results
The average scattering cross section obtained from Equation (13) are found in Figures 9-11 and Figures 12-14 they shows their relative errors for the calculation of the average scattering cross section. The nuclear parameters used can be found in Table 1 [2].
From the Figures 9-11 it is possible to see that the results obtained with the method presented, Equation (13), overlapped those obtained from the numerical reference method, being compatible with the results obtained with the method proposed by Padé.

Figure 9. Average scattering cross sections of the E0 = 6.67 eV resonance for the 238U isotope and T = 1500 K.
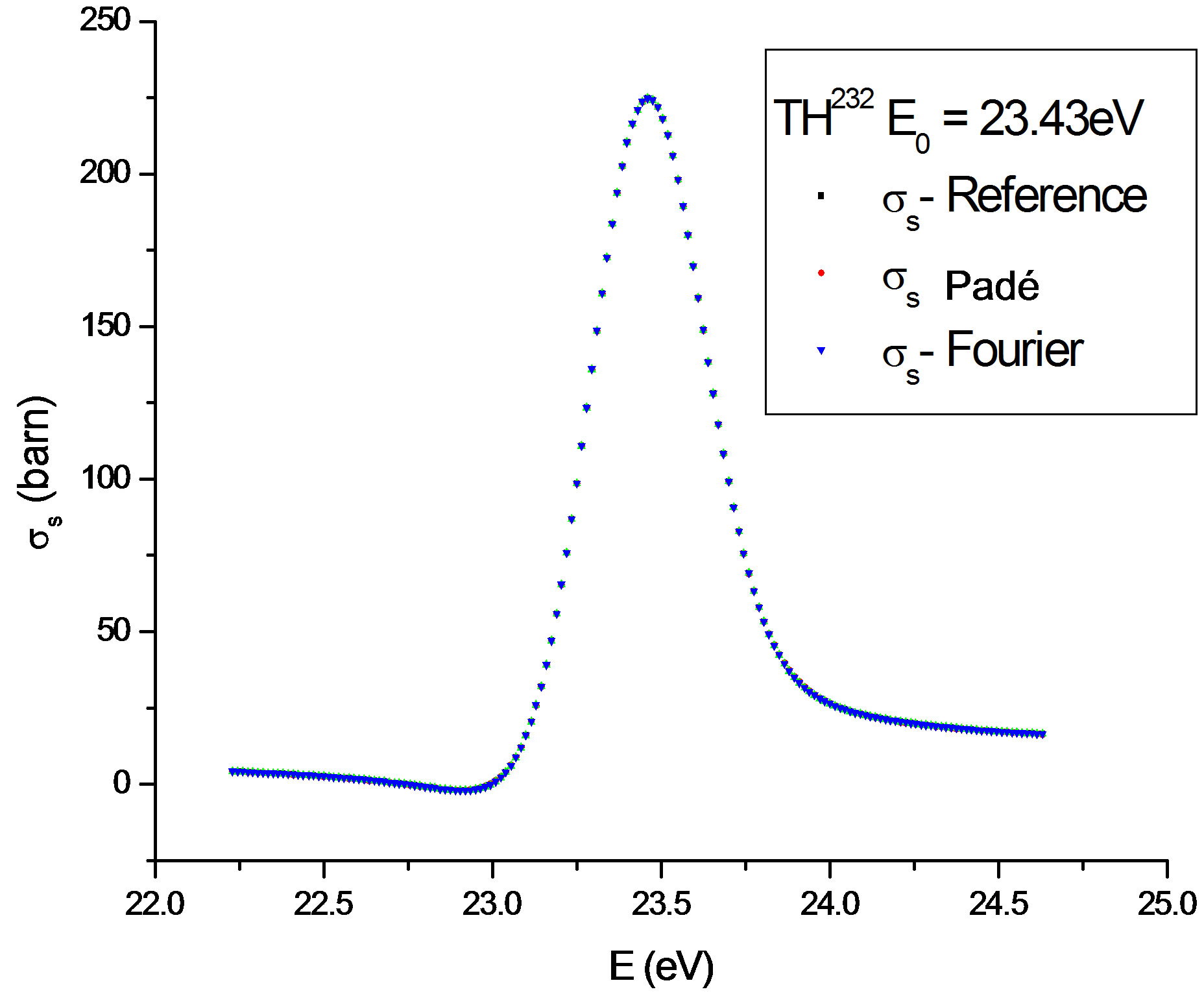
Figure 10. Average scattering cross sections of the E0 = 23.43 eV resonance for the 232Th isotope and T = 1500 K.
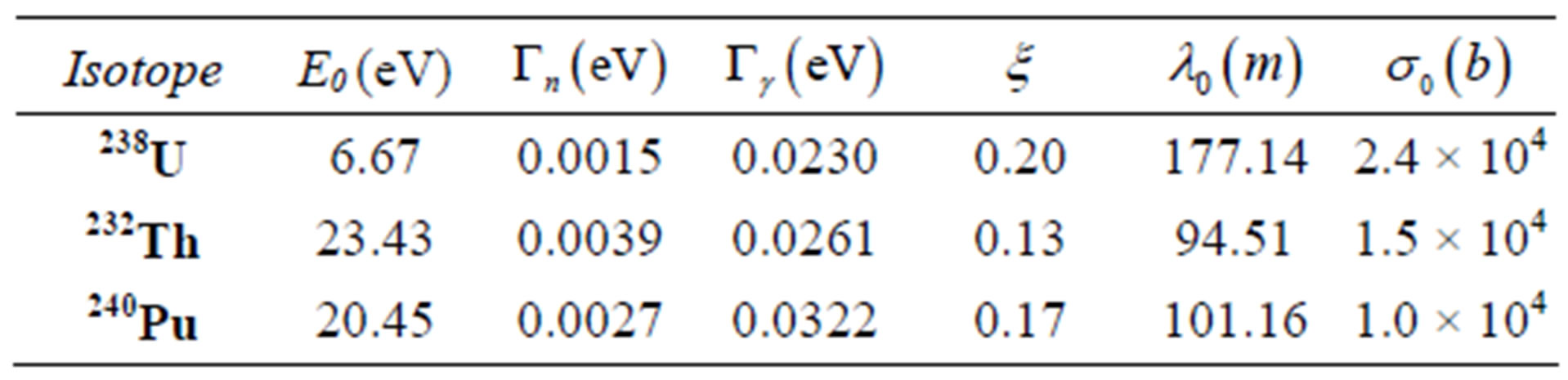
Table 1. Parameter used in the calculation of for average scattering cross sections for the 238U, 232Th and 240Pu isotope, σ = 10 barn and T = 1500 K.

Figure 11. Average scattering cross sections of the E0 = 20.45 eV resonance for the 240Pu isotope and T = 1500 K.

Figure 12. Relative error for average scattering cross sections of the E0 = 6.67 eV resonance for the 238U isotope and T = 1500 K.
From the Figures 12 to 14 it is possible to conclude that the expression proposed in this paper presents results that overlap the numerical reference method.
5. Conclusion
This paper presents a simple and precise formulation for the Doppler broadening function 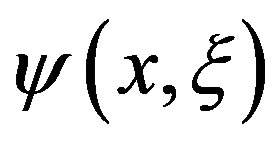 and of the interference term
and of the interference term 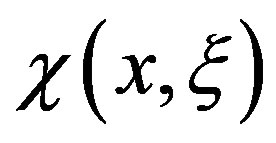 based in sine and cosine Fourier transforms proposed by Goncalves et al. Expanding the function
based in sine and cosine Fourier transforms proposed by Goncalves et al. Expanding the function 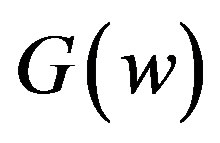 in Fourier Series was possible to obtain an accurate analytical expression for the average scattering cross section, Equation (13), that can be an alternative to other methods existing in the literature.
in Fourier Series was possible to obtain an accurate analytical expression for the average scattering cross section, Equation (13), that can be an alternative to other methods existing in the literature.

Figure 13. Relative error for average scattering cross sections of the E0 = 23.43 eV resonance for the 232Th isotope and T = 1500 K.

Figure 14. Relative error for average scattering cross sections of the E0 = 20.45 eV resonance for the 240Pu isotope and T = 1500 K.
6. Acknowledgements
The authors acknowledge the support provided by Brazilian Council for Scientific and Technological Development (CNPq) in the developing of this research.
REFERENCES
- D. A. P. Palma and A. S Martinez, “A Faster Procedure for the Calculation of the
 ,” Annals of Nuclear Energy, Vol. 36, No. 10, 2009, pp. 1516-1520. doi:10.1016/j.anucene.2009.07.019
,” Annals of Nuclear Energy, Vol. 36, No. 10, 2009, pp. 1516-1520. doi:10.1016/j.anucene.2009.07.019 - A. Talamo, “Analytical Calculation of the Fuel Temperature Reactivity Coefficient for Pebble Bed and Prismatic High Temperature Reactors for Plutonium and UraniumThorium Fuels,” Annals of Nuclear Energy, Vol. 34, No. 1-2, 2007, pp. 68-82. doi:10.1016/j.anucene.2006.11.003
- S. G. Hong and K. S. Kim, “Iterative Resonance SelfShielding Methods Using Resonance Integral Table in Heterogeneous Transport Lattice Calculations,” Annals of Nuclear Energy, Vol. 38, No. 1, 2011, pp. 32-43. doi:10.1016/j.anucene.2010.08.022
- D. A. Palma, A. Z. Mesquita, R. M. G. P. Souza and A. S. Martinez, “Real-Time Monitoring of Power and Neutron Capture cross Section of Nuclear Research Reactor,” In: International Conference on Research Reactors: Safe Management and Effective Utilization, International Atomic Energy Agency, Vienna, 2011.
- W. M. Stacey, “Nuclear Reactor Physics,” Wiley, New York, 2001.
- A. C. Gonçalves, A. S. Martinez and F. C. Silva, “Solution of the Doppler Broadening Function Based on the Fourier Cosine Transform,” Annals of Nuclear Energy, Vol. 35, No. 10, 2008, pp. 1878-1881. doi:10.1016/j.anucene.2008.04.003
- G. Arfken and H. Weber, “Mathematical Method for Physicists,” Academic Press Inc., London, 2001.
- C. M. Amaral and A. S. Martinez, “The Effect of Scattering Interference Term on Pratical Width,” Annals of Nuclear Energy, Vol. 28, No. 11, 2001, pp. 1133-1143. doi:10.1016/S0306-4549(00)00112-2
- R. S. Keshavamurthy and R. Harish, “Use of Padé Approximations in the Analytical Evaluation of the
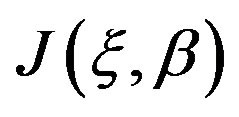 Function and Its Temperature Derivative,” Nuclear Science and Engineering, Vol. 115, No. 1, 1993, pp. 81-88.
Function and Its Temperature Derivative,” Nuclear Science and Engineering, Vol. 115, No. 1, 1993, pp. 81-88. - D. A. Palma, A. C. Gonçalves and A. S. Martinez, “An Alternative Analytical Formulation for the Voigt Function Applied to Resonant Effects in Nuclear Processes,” Nuclear Instruments & Methods in Physics Research. Section A, Accelerators, Spectrometers, Detectors and Associated Equipment, Vol. 654, No. 1, 2011, pp. 406- 411. doi:10.1016/j.nima.2011.07.029

