World Journal of Nuclear Science and Technology
Vol.2 No.1(2012), Article ID:17037,6 pages DOI:10.4236/wjnst.2012.21004
A Closed-Form Formulation for the Build-Up Factor and Absorbed Energy for Photons and Electrons in the Compton Energy Range in Cartesian Geometry
Department of Applied Math, Universidade Federal do Rio Grande do Sul, Porto Alegre, Brazil
Email: {borges, julio.lombaldo, bardo.bodmann, vilhena}@ufrgs.br
Received October 5, 2011; revised November 26, 2011; accepted December 8, 2011
Keywords: Build-Up Factor; Compton Energy; Cartesian Geometry; Fokker-Plank Equation
ABSTRACT
In this work, we report on a closed-form formulation for the build-up factor and absorbed energy, in one and two dimensional Cartesian geometry for photons and electrons, in the Compton energy range. For the one-dimensional case we use the LTSN method, assuming the Klein-Nishina scattering kernel for the determination of the angular radiation intensity for photons. We apply the two-dimensional LTSN nodal solution for the averaged angular radiation evaluation for the two-dimensional case, using the Klein-Nishina kernel for photons and the Compton kernel for electrons. From the angular radiation intensity we construct a closed-form solution for the build-up factor and evaluate the absorbed energy. We present numerical simulations and comparisons against results from the literature.
1. Introduction
In radiological protection the effectiveness of a material as a biological shield is related to its cross-section for scattering and absorption which is cast into physical parameters. The determination of those parameters require the solution of a systems of linear transport equations, i.e. the fluence for photons and electrons. Established methods that solve the transport equations are the PN approximation [1], the discrete ordinate method and their variants [2]. The SN method has been used successfully in photon transport calculation, whereas recently the PN approximation was applied to electron transport. In this work we present the solution of a couple system of linear transport equations, using the LTSN method for a rectangular domain considering the Klein-Nishina scattering kernel and a multi-group model for photons. The electron contribution to energy deposition induced by incident photons is quantified solving the two-dimensional Fokker-Planck equation for electron transport [3,4] by the PN approximation in the angular variable followed by applying the Laplace Transform to one of the spatial variables (here x). This procedure leads to a closed-form formulation for the build-up factor and absorbed energy, in one and two dimensional Cartesian geometry for photons and electrons, in the energy range where Compton scattering is dominant [5].
2. The LTSN Nodal Solution in Two Dimensional for Photons
The two-dimensional SN nodal problem for photons, assuming Klein-Nishina scattering kernel and a multi-group model is
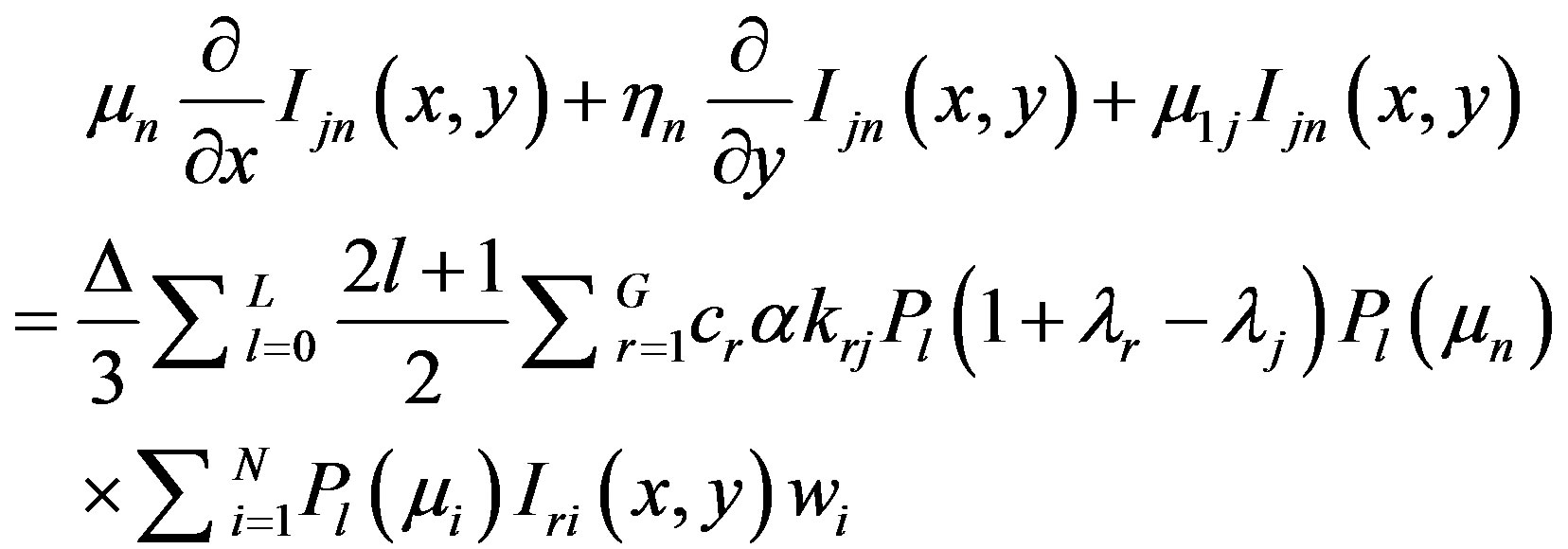 (1)
(1)
subject to vacuum boundary conditions in a rectangle 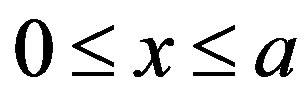 and
and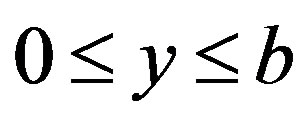 . Where
. Where 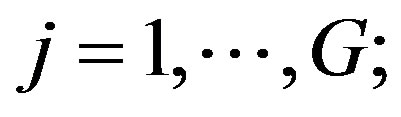 n = 1,
n = 1, , N;
, N;  is the cardinality of the discrete ordinate set, M represents the order of the angular quadrature, G is the number of energy groups in units of wavelengths,
is the cardinality of the discrete ordinate set, M represents the order of the angular quadrature, G is the number of energy groups in units of wavelengths,  is the linear attenuation coefficient,
is the linear attenuation coefficient,
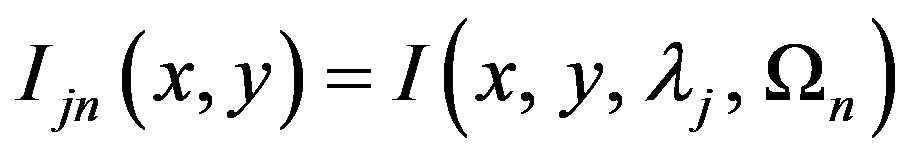 is the angular flux into the discrete direction
is the angular flux into the discrete direction  for the j-th energy group,
for the j-th energy group,  are the Lewis-Miller quadrature weights and
are the Lewis-Miller quadrature weights and  is the Klein-Nishina scattering kernel, defined as
is the Klein-Nishina scattering kernel, defined as
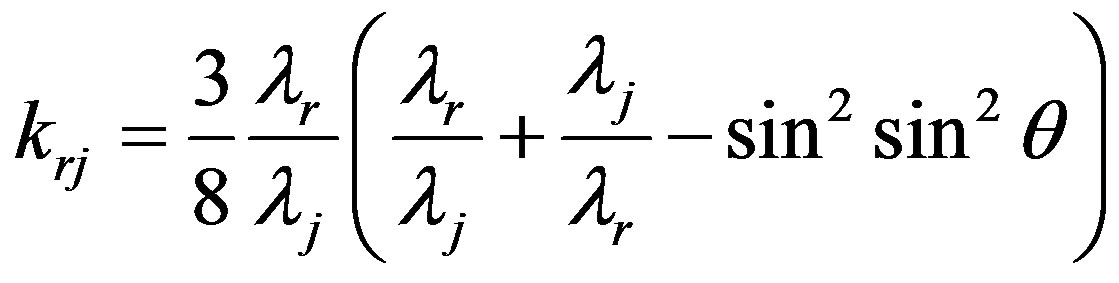 (2)
(2)
The LTSN nodal approach for photons yields the following SN equation system
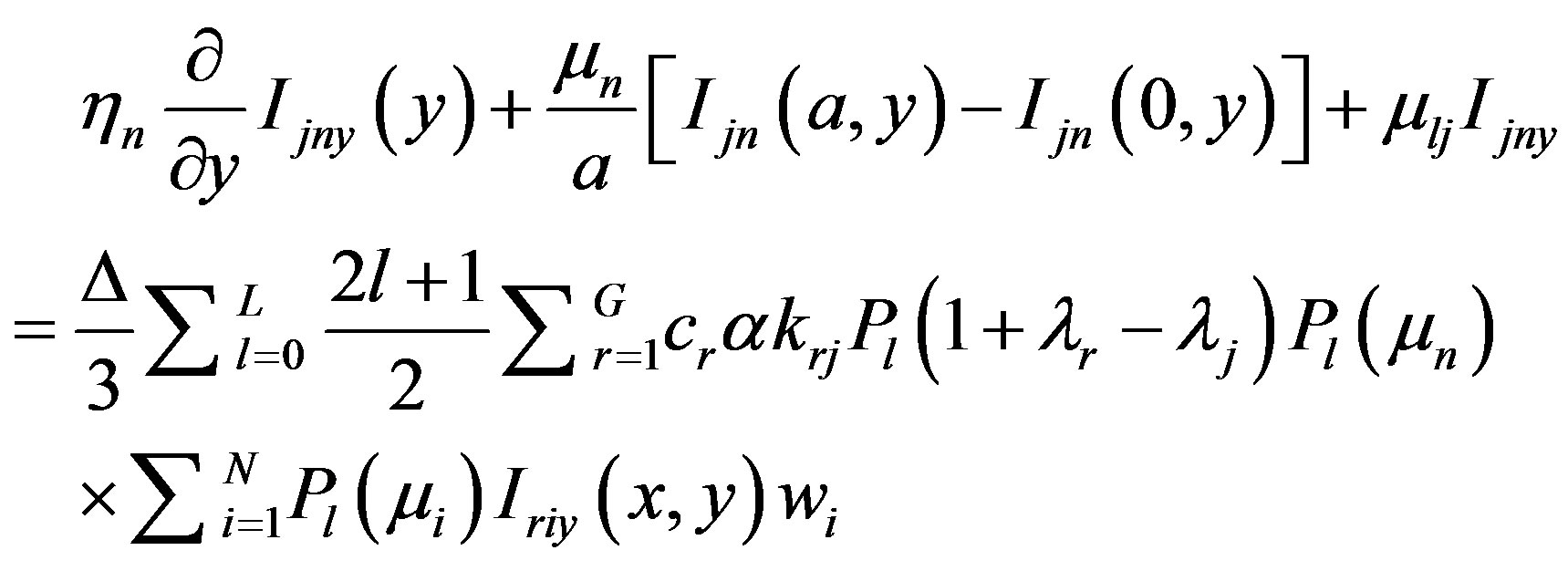 (3)
(3)
For  and
and . Here
. Here  and
and 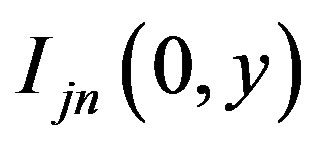 are the angular fluxes at the boundary edges with
are the angular fluxes at the boundary edges with  and the average angular flux is
and the average angular flux is
 (4)
(4)
Further,
 (5)
(5)
For  and
and  N. In Equation (5),
N. In Equation (5), 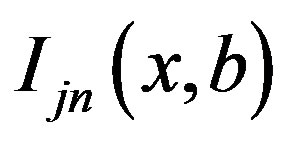 and
and  are the angular fluxes at the boundary edges with y = 0, y = b and the average angular flux is
are the angular fluxes at the boundary edges with y = 0, y = b and the average angular flux is
 (6)
(6)
Application of the LTSN method consists in Laplace transform of the set of SN equations and solving the resulting algebraic equations by matrix diagonalization and subsequent inversion of the transformed angular flux by standard procedures of integral transform theory. The Laplace transform of Equation (3) is
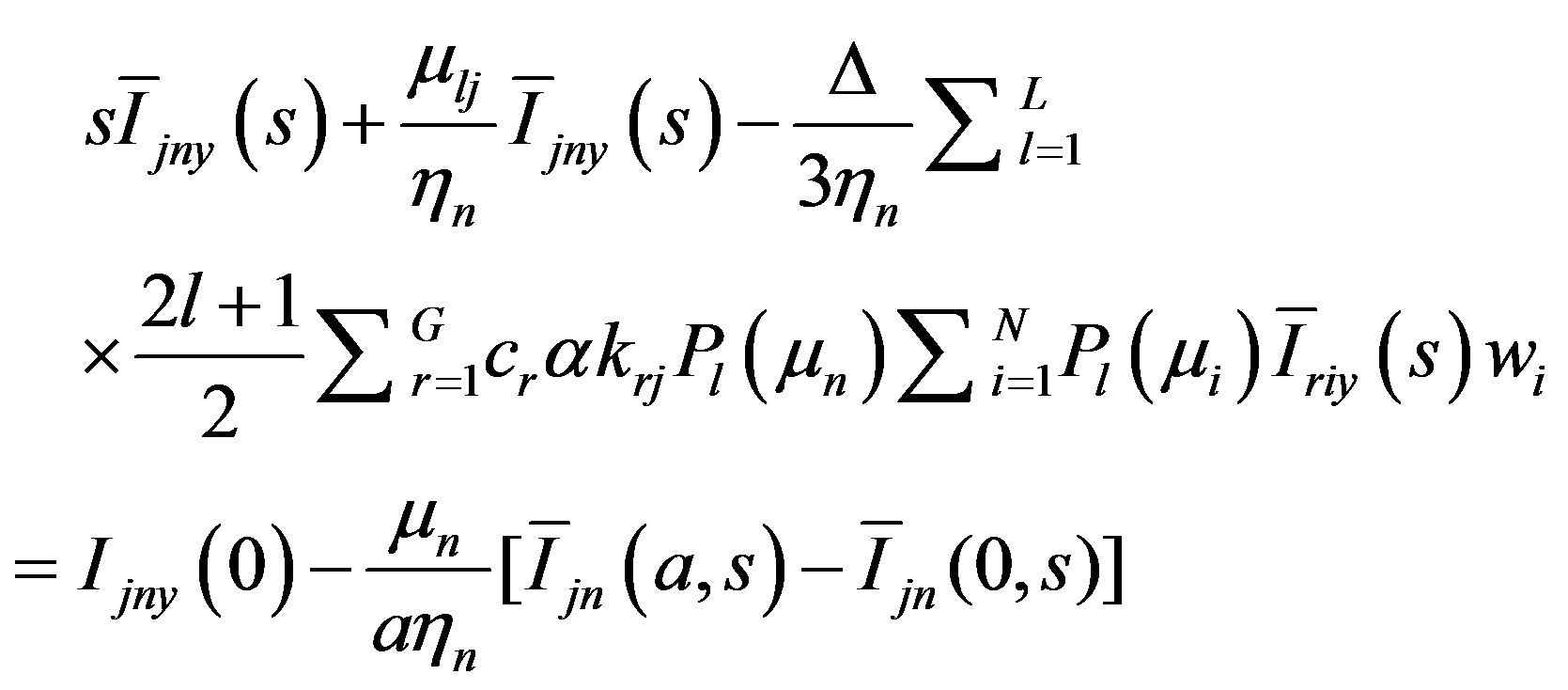 (7)
(7)
For  and
and  which can be cast in matrix form,
which can be cast in matrix form,
 (8)
(8)
Here, 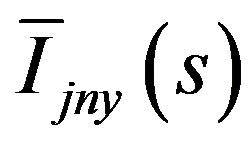 are the N componentes of the Laplace transformed angular flux in the y variable and
are the N componentes of the Laplace transformed angular flux in the y variable and 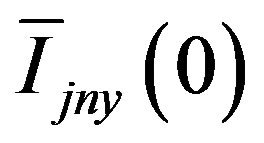 are the respective components of the angular flux at the edge y = 0. The components have the following forms,
are the respective components of the angular flux at the edge y = 0. The components have the following forms,
 (9)
(9)
and
 (10)
(10)
The components of the matrix 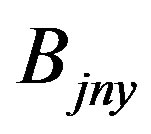 are given by,
are given by,
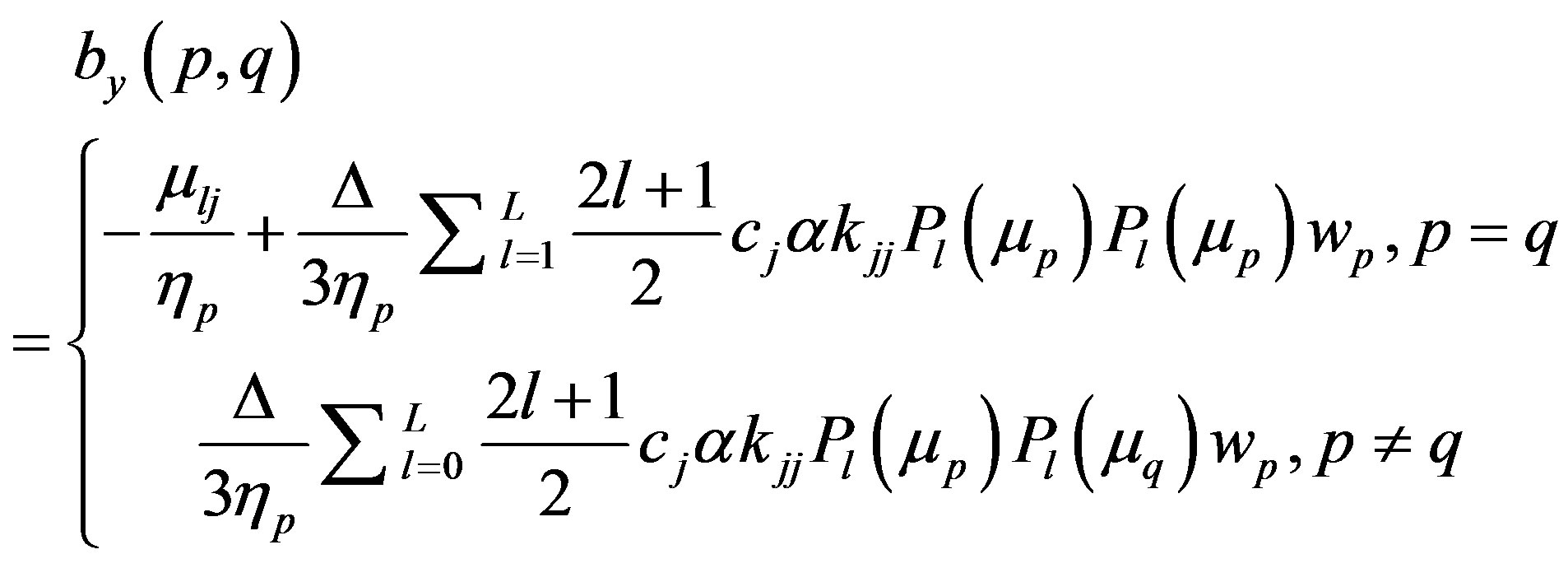
The scattering term is,
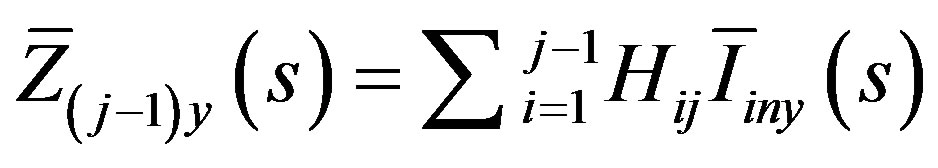 (11)
(11)
with the components of matrix Hij (see the equation below).
The vector  has the components,
has the components,
 (12)
(12)
A similar methodology in the x variable leads to the linear algebric system which can be matrix form,
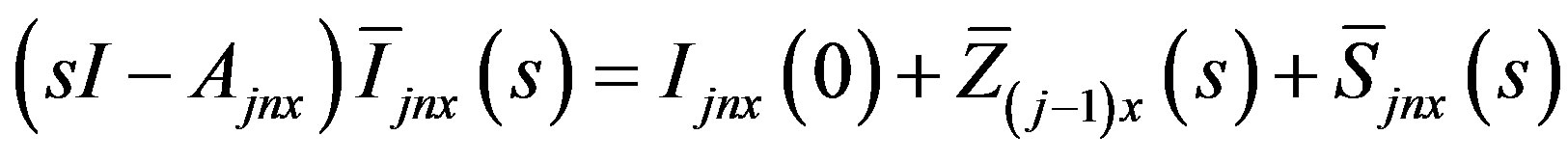 (13)
(13)
where 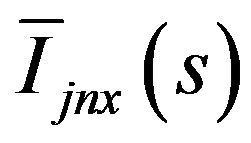 has the following form,
has the following form,
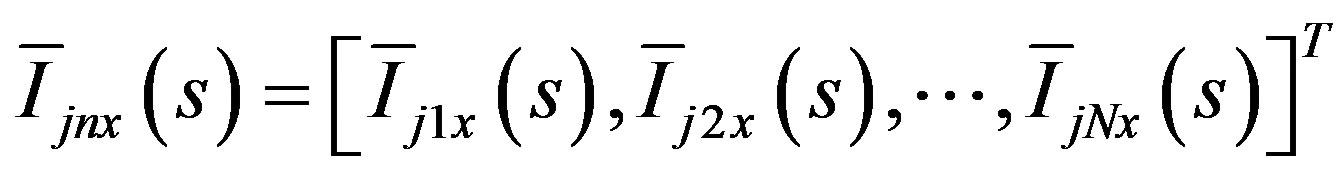 (14)
(14)
The matrix elements of  are,
are,

and the scattering term is
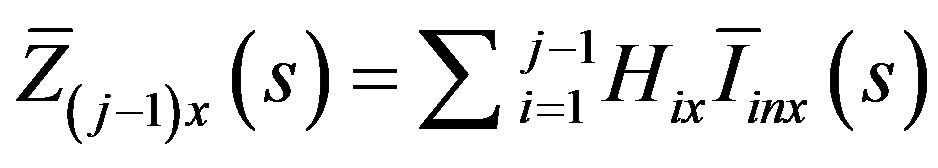 (15)
(15)
where the matrix elements of 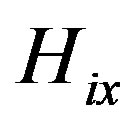 are given
are given
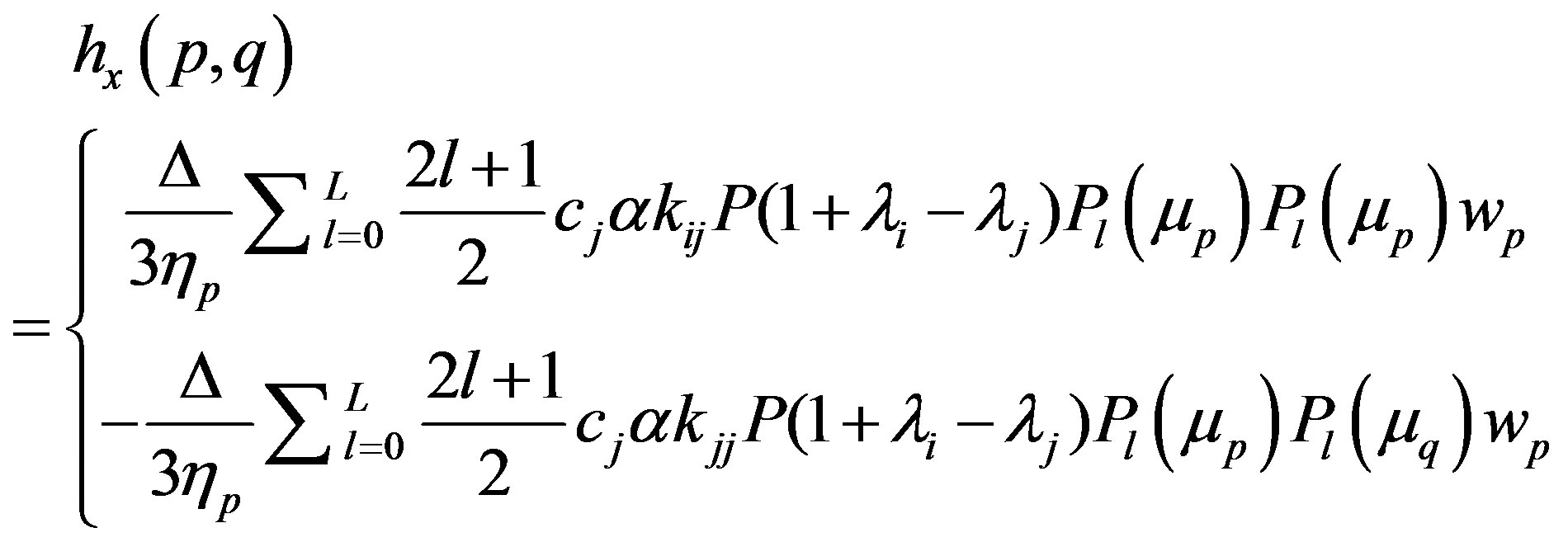
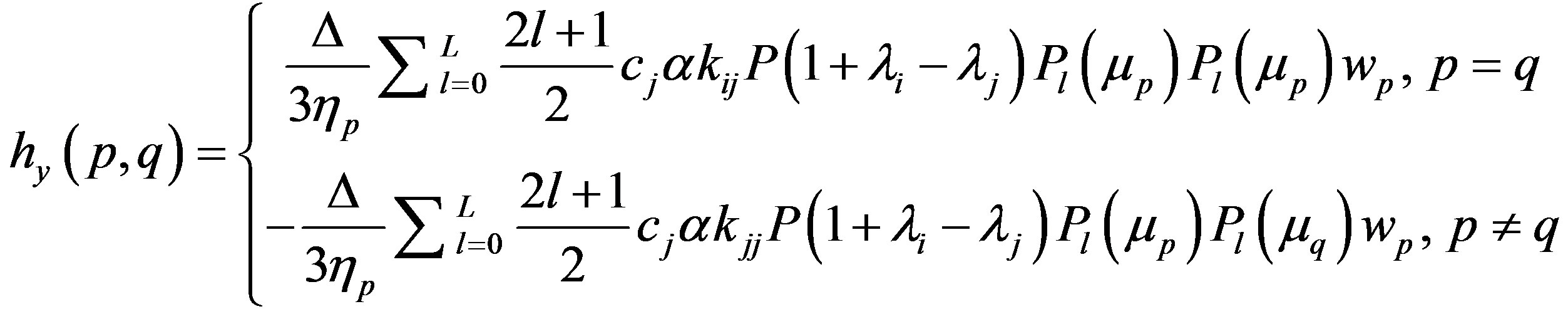
and the vector 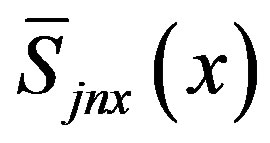 is
is
 (16)
(16)
The LTSN solution for Equations (8) and (16) are given by
 (17)
(17)
and
 (18)
(18)
Taking the Laplace inversion by applying the Heaviside expansion yields
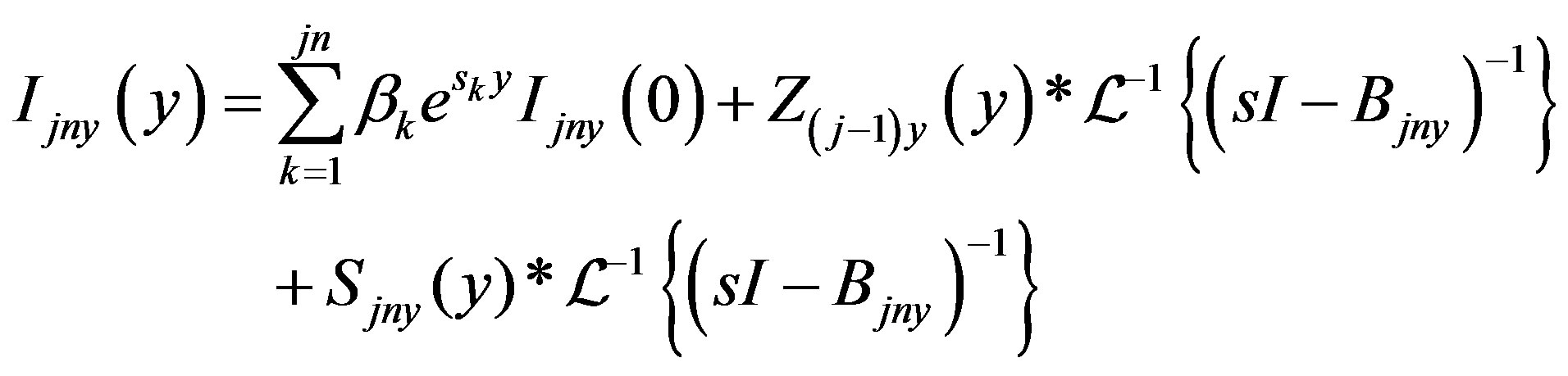 (19)
(19)
and
 (20)
(20)
For the fluxes at boundary one may use reasonable approximation [6]
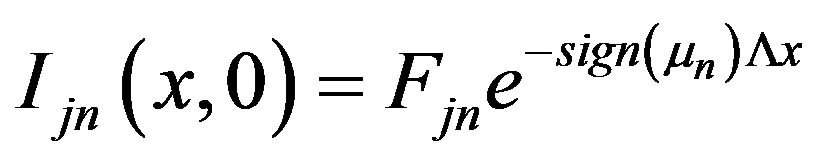 (21)
(21)
 (22)
(22)
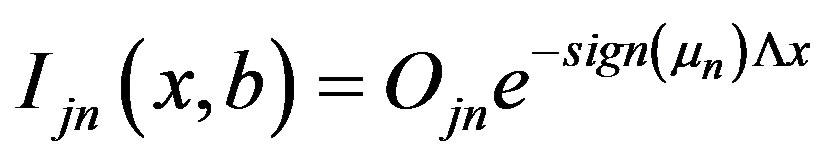 (23)
(23)
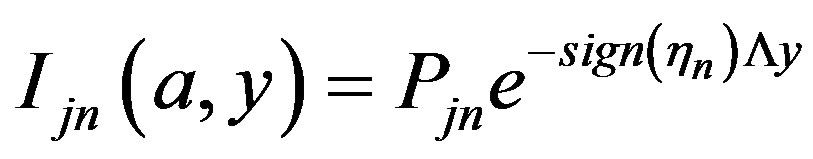 (24)
(24)
Here the signal function follows the usual definition  for
for  and
and 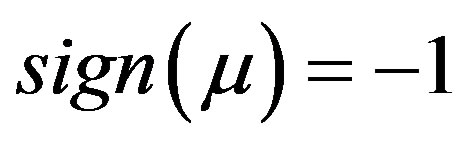 for
for  and
and  represents an attenuation parameter, here the macroscopic absorption crosssection.
represents an attenuation parameter, here the macroscopic absorption crosssection.
The generalization of the LTSN nodal solution for a heterogeneous rectangular geometry assuming the Klein-Nishina scattering kernel and a multi-group model may be implemented in a completely analogue procedure. In such a problem the LTSN solution is determined for each subdomain and the integration constants are evaluated upon applying the boundary and interface.
3. The Two-Dimensional Fokker-Planck Equation Solution for Electrons
The purpose of radiation transport is to determine how particles move through materials and what effects their propagation have on the material through the mechanisms of deposited energy and charge deposition. The angular flux of electrons in a rectangular domain can be determined by solving the following two-dimensional, time independent electron transport equation, in a rectangle  and
and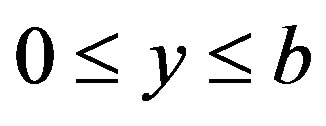 , subject to vacuum boundary conditions.
, subject to vacuum boundary conditions.
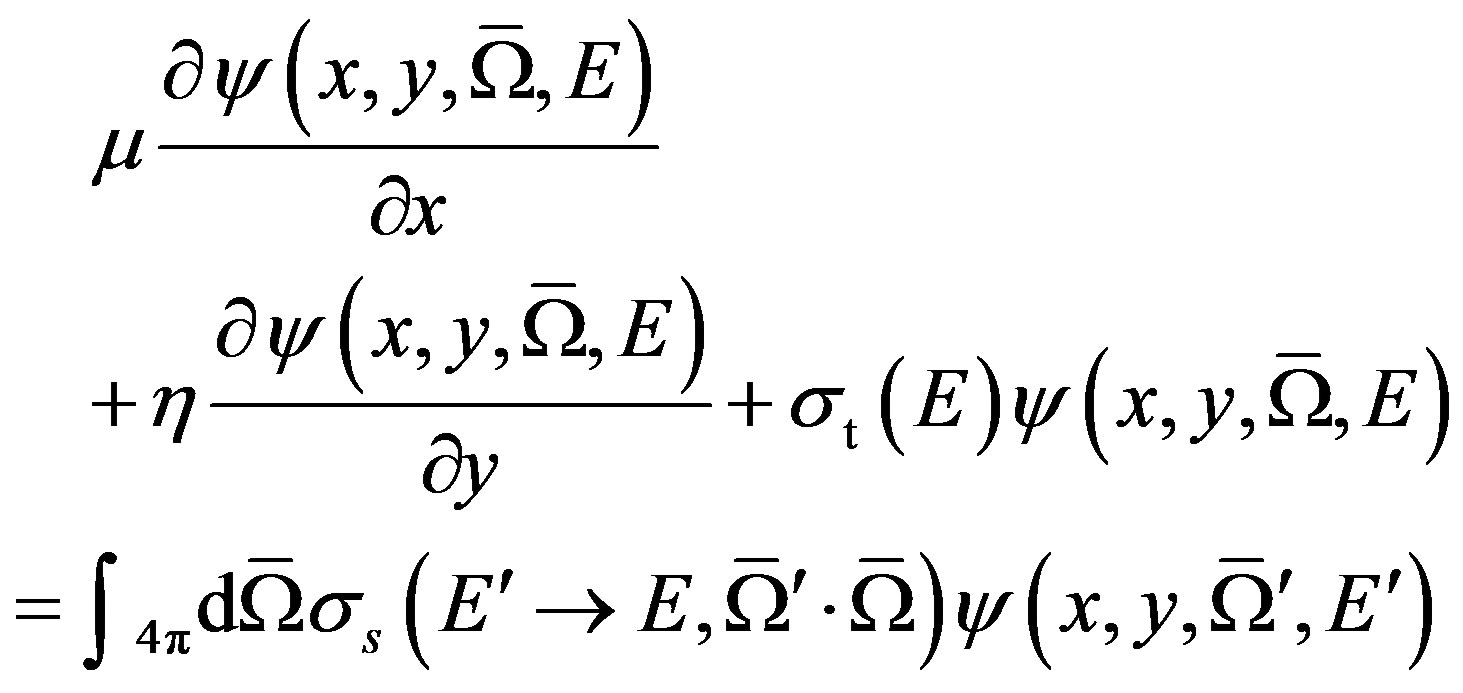 (25)
(25)
Here, the angular flux , represents the flux of particles at position (x, y), with energy E travelling in direction
, represents the flux of particles at position (x, y), with energy E travelling in direction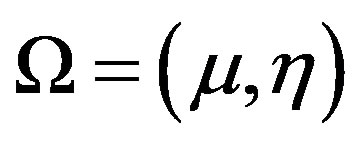 . The quantity
. The quantity  in Equation (25) is the differential scattering cross-section, in this work, we focus on screened Rutherford scattering which is
in Equation (25) is the differential scattering cross-section, in this work, we focus on screened Rutherford scattering which is
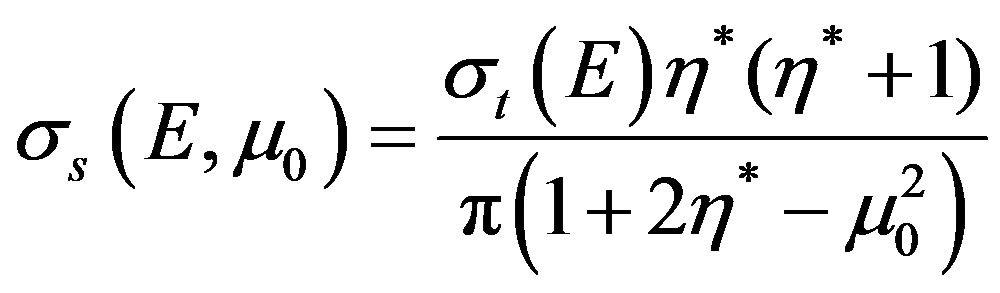 (26)
(26)
where 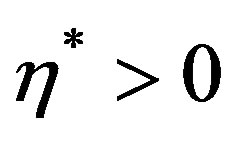 is typically a small constant called the screening parameter parameter is given by
is typically a small constant called the screening parameter parameter is given by
 (27)
(27)
with Z the atomic number of the nucleus, mv the relativistic momentum of the scattered electron and
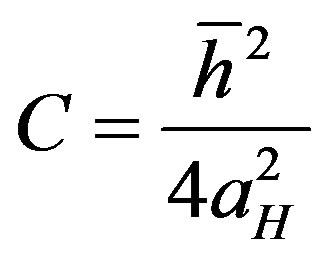 (28)
(28)
which  is Planck’s constant and
is Planck’s constant and 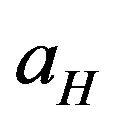 is the Bohr radius.
is the Bohr radius.
We assume that the Fokker-Planck (FP) scattering description is appropriate, so that the transport problem (25) is given by,
 (29)
(29)
Here the coefficient  is he transport cross-sectionand defined as,
is he transport cross-sectionand defined as,
 (30)
(30)
Upon multiplying Equation (29) by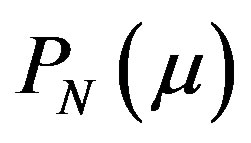 , integrating over
, integrating over  and using the recursion formula, as well as general properties of Legendre polynomials leads to the following PN equations
and using the recursion formula, as well as general properties of Legendre polynomials leads to the following PN equations
 (31)
(31)
The angular flux moments in discrete ordinates may be expressed using a quadrature approximation,
 (32)
(32)
For 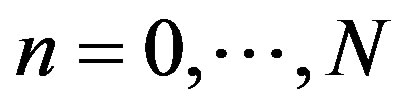 with
with  in the PN approximation and Tn represented by an integral term which can be solved analytically,
in the PN approximation and Tn represented by an integral term which can be solved analytically,
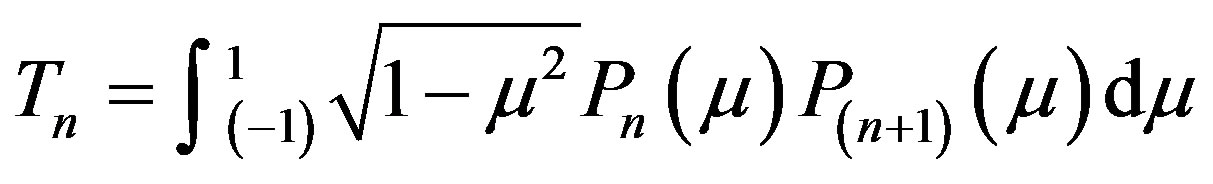 (33)
(33)
After applying the Laplace transform in Equation (31) in the spatial variable x, we came out with the linear algebric system,
 (34)
(34)
For  and where
and where  and
and  are the transformed angular fluxes in the spatial x variable. Equation (36) can be cast in matrix form,
are the transformed angular fluxes in the spatial x variable. Equation (36) can be cast in matrix form,
 (35)
(35)
where  are the N components of the derivative of the Laplace transformed angular flux in the x variable.
are the N components of the derivative of the Laplace transformed angular flux in the x variable.
 (36)
(36)
The components of matrices  and CN are for
and CN are for , respectively
, respectively
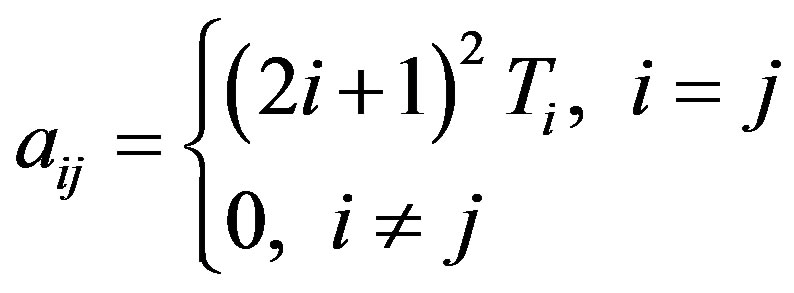


The solution of Equation (35) is
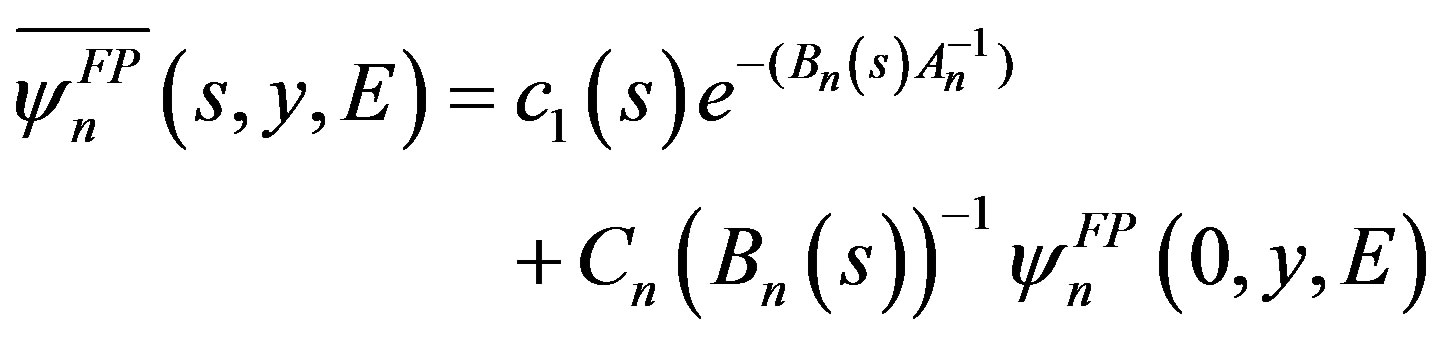 (37)
(37)
where 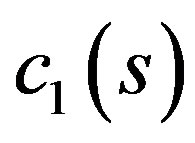 is an arbitrary constant determined by applying the boundary and interface conditions. Due to the linear character of the inverse Laplace transform operator, the solution is composed by
is an arbitrary constant determined by applying the boundary and interface conditions. Due to the linear character of the inverse Laplace transform operator, the solution is composed by
 (38)
(38)
4. Numerical Results
In the following we apply the closed-form formulation to the build-up factor and absorbed energy for photons and electrons in the Compton energy range and in Cartesian geometry. Moreover, we the one-dimensional, two-dimensional problem for photons and two-dimensional problem for photons and electrons. To this end we evaluate the exposure build-up factor, considering a scalar flux of the photons with energy 1 MeV, incident in a multi-layered slab with two regions, composed of water and lead, water and iron, lead and iron. Assuming that the kernel is described by the Klein-Nishina differential scattering crosssection and the energy variables may be simplified in form of a multi-group model in the wavelength (energy) variable.
Here the exposure build-up factor is defined as the sum of the product of the attenuation coefficient of the air with the scalar flux for all photons, including the incident flux, divided by the attenuation coefficient of the air for the incident flux multiplied by the incident scalar flux. The numerical results for three problems are shown in Table 1 for water and lead, in Table 2 for water and iron and in Table 3 for lead and iron. In Table 1 we present the LTSN numerical simulations for the exposure build-up factor and comparisons with results from the EGS4 code [7] generated for the one-group model. We consider a multi-layered slab with two regions, composed of water (μij = 0.0707 cm2/g and 1.0 mpf) and lead (μij = 0.06848 cm2/g and depth in multiples of the mean free path, 4.0, 5.0, 10.0, 20.0, 30.0 and 40.0 mfp) together with the afore mentioned vacuum boundary conditions.
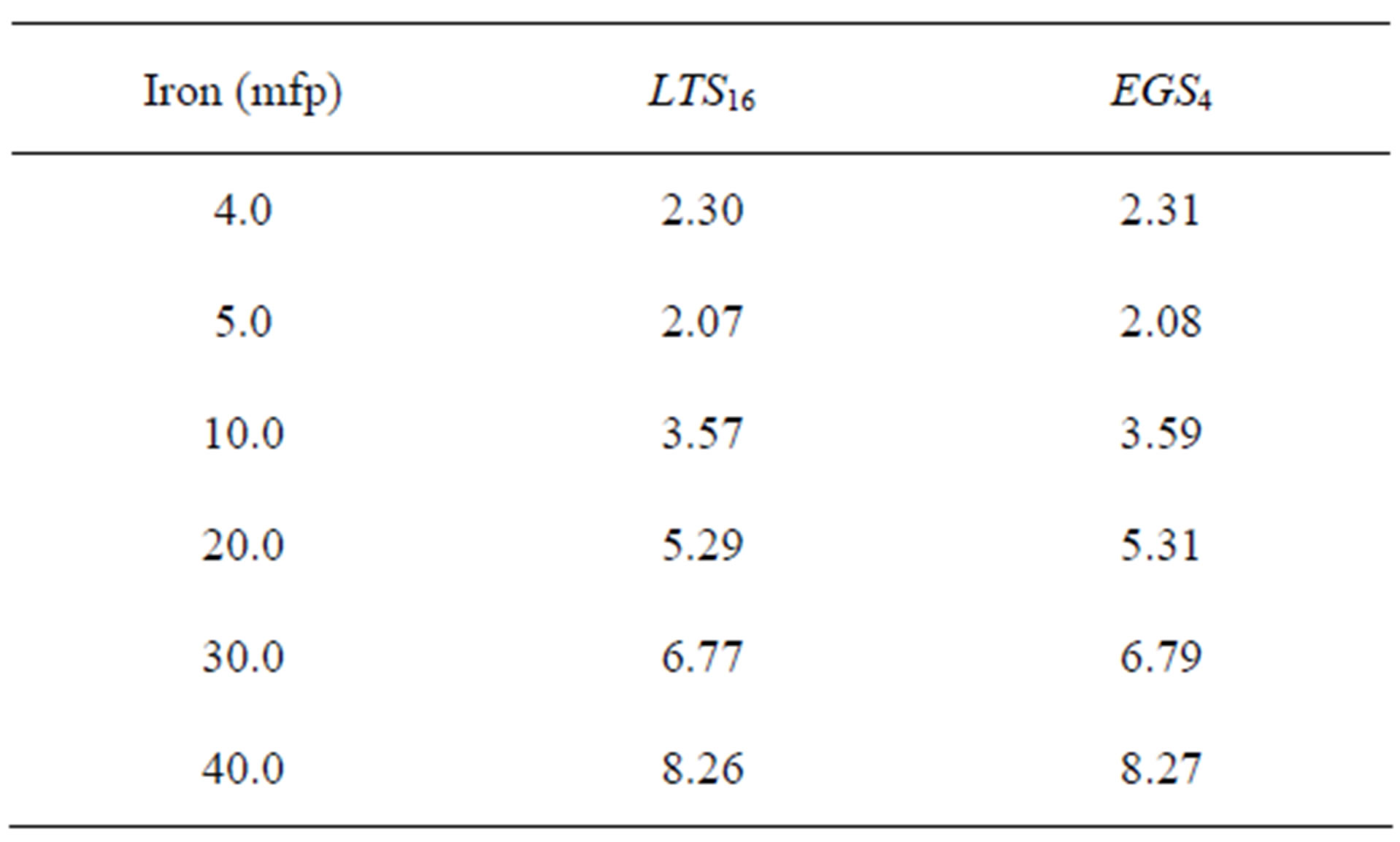
Table 1. Numerical exposure buildup factor simulations for a multilayered slab composed of water (1.0 mfp) and lead.
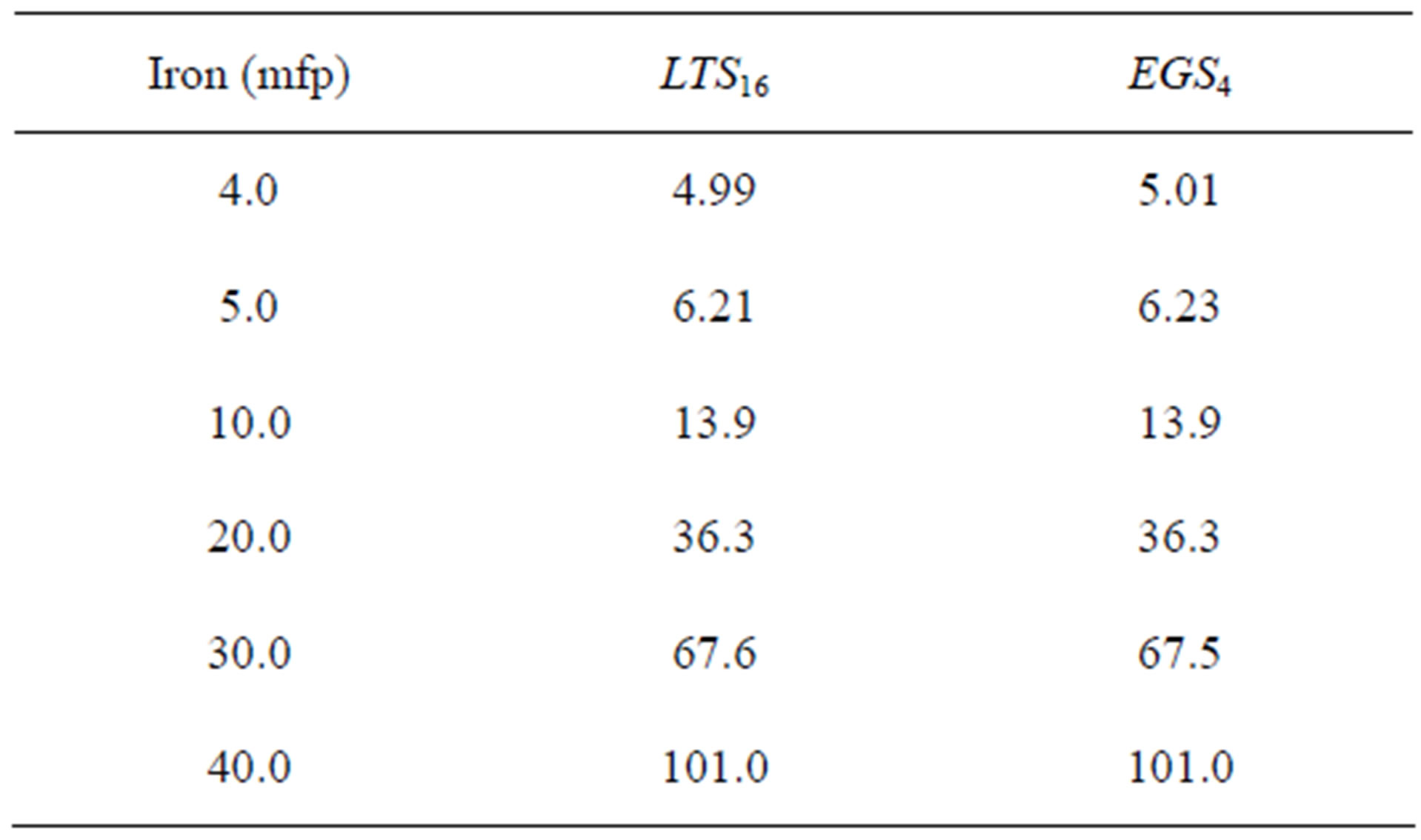
Table 2. Numerical exposure buildup factor simulations for a multilayered slab composed of water (1.0 mfp) and iron.

Table 3. Numerical exposure buildup factor simulations for a multilayered slab composed of lead (1.0 mfp) and iron.
In Table 2 we present the LTSN numerical simulations for the exposure build-up factor and comparisons with the results from EGS4 generated for the one-group model. We consider a multi-layered slab with two regions, composed of water (μij = 0.0707 cm2/g with depth of 1.0 mpf) and iron (μij = 0.0596 cm2/g with depth 4.0, 5.0, 10.0, 20.0, 30.0 and 40.0 mfp) and vacuum boundary conditions.
From the analysis of the results encountered in Tables 1-3, one realizes a fairly good agreement between the LTS16 and EGS4 results. The numerical convergence of the LTSN results showed for increasing N a coincidence of six significant digits for N = 14 and N = 16. For two-dimensional problems for photons and electrons, we applied the LTSN method, for N = 8, in the transport equation for photons and used N = 9 in the PN approximation for the angular variable of the Fokker-Planck equation for electrons. We considered homogeneous rectangular geometries composed of water liquid (Z/A = 0.55508, ρ = 1 g/cm2), soft tissue (ICRU44, Z/A = 0.54996, ρ = 1.06 g/cm2) and cortical bone (ICRU44, Z/A = 0.51478, ρ = 1.92 g/cm2). Further, we assumed a mono-energetic (E = 1.25 MeV) and monodirectional photon beam incident on the edge of a rectangle with dimension 20 cm × 20 cm and vacuum boundary conditions. The incoming photons were tracked until their whole energy was deposited and/ or they left the domain of interest. In this problem also the energy deposited by the secondary electrons, generated by the Compton Effect, were considered. Other possible effects, however with small or spurious contributions were not taken into account. The numerical results encountered for absorbed energy in the domain were compared with simulations obtained with the program Geant4 v8 [8], using the low energy libraries and are presented in Tables 4 and 5.
The numerical convergence of the LTSN results showed for increasing N a coincidence of three significant digits for N = 4, 6 and 8. Notice, the coincidence of four significant digits for the PN approximation with N = 7 and 9. These results were obtained in the homogeneous domain with dimension 20 cm × 20 cm that was composed of water. In Table 4 we present the LTS8 nodal numerical simulations for the absorbed energy induced by photons incident on a homogeneous rectangular domain, that is composed of a variety of different materials. In Table 5 we present numerical simulations for absorbed energy by the P9 approximation, due to free electrons, arising from Compton scattering in a homogeneous rectangular domain composed of different materials. These results were compared with simulations obtained by Geant4.
In spite of the fact, that two different methods were used to simulate energy deposition, the Monte Carlo method with Geant4 and our closed form solution the results in Tables 4 and 5 show a fairly good agreement. From the results, we notice that the maximum discrepancy found is 3.4% in the simulations for photons and 8.3% for electrons. The difference of our numerical results in comparison to the Geant simulations, that contain a catalogue of processes, demonstrate that other effects shall be taken into account. As the material density increases, the
Table 4. Absorved energy (KeV/photon emitted from the source) by the photons incident in a homogeneous domain dimension 20 cm × 20 cm, composed of materials different.
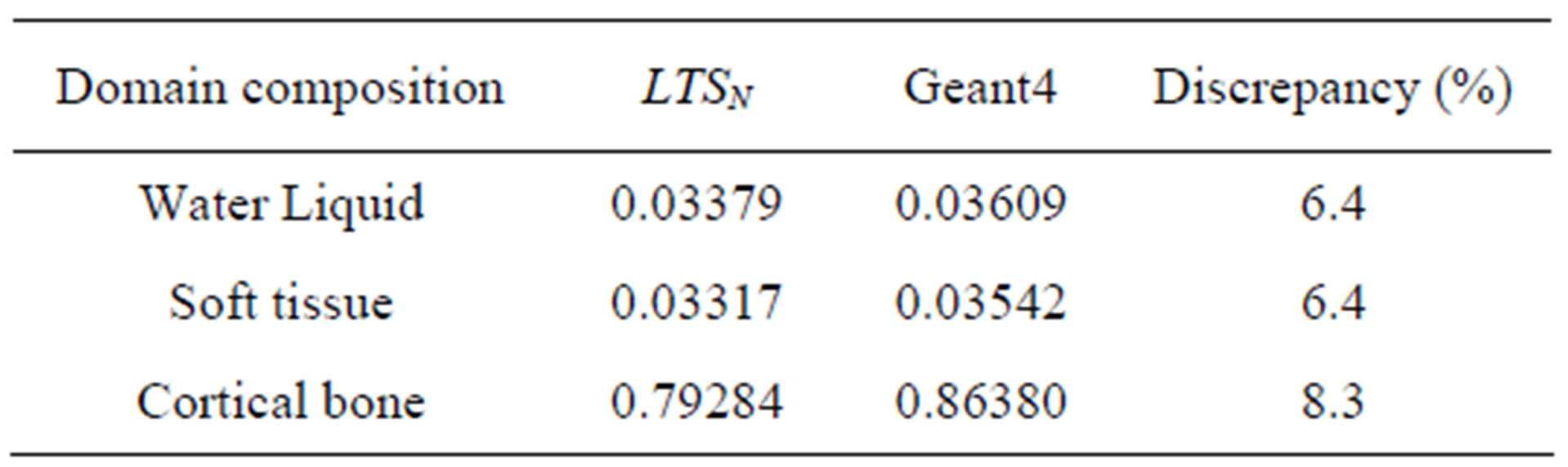
Table 5. Absorved energy (KeV/photon emitted from the source) by the free electrons in a homogeneous domain dimension 20 cm × 20 cm, composed of materials different.
number of interactions increases as well as the possibility of other production processes involving secondary electrons, responsible for more than 86% of the total energy absorbed in domain.
5. Conclusion
Concluding, we were successful in determinig the LTSN solution in closed form forenergy deposition induced by photons in Cartesian geometry. From the solution we obtained the buildup factor and absorbed energy, for photons and electrons, in the Compton energy range. It is worth mentioning, that the LTSN procedure maintains an analytical character of the solution and the unique approximation made was in the leakage angular flux at the boundary. The PN solution of the Fokker-Planck equation remains analytical in the sense that no approximation is made along its derivation from PN equations, except for the truncation. Finally, a variety of additional numerical experiments have shown us that the presented method is robust for problems of the considered transport equation type.
6. Acknowledgements
The authors are gratefully to CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico) for the partial financial support of this work. A special acknowledgment for the project INCT (Instituto Nacional de Ciencia e Tecnologia—Reatores Nucleares Inovadores) for financial support.
REFERENCES
- C. F. Segatto, M. T. Vilhena and R. P. Pazos, “On the Convergence of the Spherical Harmonics Approximations,” Nuclear Science and Engineering, Vol. 134, No. 1, 2000, pp. 114-119.
- M. T. Vilhena, C. F. Segatto and L. B. Barichello, “A Particular Solution for the SN Radiative Transfer Problems,” Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 53, No. 4, 1995, pp. 467-469. doi:10.1016/0022-4073(95)90020-9
- C. Borges and E. W. Larsen, “The Transversely Integrated Scalar Flux of a Narrowly Focused Particle Beam,” SIAM Journal on Applied Mathematics, Vol. 55, No. 1, 1995, pp. 1-22.
- C. Borges and E. W. Larsen, “On the Accuracy of the Fokker-Planck and Fermi Pencil Beam Equation for Charged Particle Transport,” Medical Physics, Vol. 23, No. 10, 1996, pp. 1749-1759. doi:10.1118/1.597832
- B. D. A. Rodriguez, M. T. Vilhena, V. Borges and G. Hoff, “A Closed Form Solution for the Two-Dimensional Fokker-Planck Equation for Electron Transport in the Range of Compton Effect,” Annals of Nuclear Energy, Vol. 35, No. 5, 2008, pp. 958-962. doi:10.1016/j.anucene.2007.09.002
- B. D. A. Rodriguez, M. T. Vilhena and V. Borges, “A Solution for the Two-Dimensional Transport Equation for Photons and Electrons in a Rectangular Domain by the Laplace Transform Technique,” International Journal of Nuclear Energy Science and Technology, Vol. 5, No. 1, 2010, pp. 25-40. doi:10.1504/IJNEST.2010.030304
- H. Hirayama and K. Shin, “Application of the EGS4 Monte Carlo Code to a Study of Multilayer Gamma-Ray Exposure Buildup Factors,” Journal of Nuclear Science and Technology, Vol. 35, No. 11, p. 816. doi:10.3327/jnst.35.816
- D. H. Wright, “Physics Reference Manual,” 2001. http://cern.ch/geant4
- G. C. Pomraning, “Flux-Limited Diffusion and Fokker- Planck Equations,” Nuclear Science and Engineering, Vol. 85, No. 2, 1983, p. 116.
- J. Wood, “Computational Methods in Reactor Shielding,” Pergamon Press, Oxford, 1982.
- S. Agostinelli, et al., “Geant4: A Simulation Toolkit,” Nuclear Instruments and Methods in Physics Research A, Vol. 506, No. 3, 2003, pp. 250-303.
- DOORS 3.1, “One, Two and Three Dimensional Discrete Ordinates Neutron Photon Transport Code System,” Radiation Safety Information Computational Center (RSICC), Code Package CCC-650, Oak Ridge, Tennessee, 1996.
- B. D. A. Rodriguez, M. T. Vilhena and V. Borges, “The Determination of the Exposure Buildup Factor Formulation in a Slab Using the LTSN Method,” Kerntechnik, Vol. 71, No. 4, 2006, pp. 182-184.

