American Journal of Operations Research
Vol.06 No.05(2016), Article ID:70955,13 pages
10.4236/ajor.2016.65037
Adaptive Parallel Particle Swarm Optimization Algorithm Based on Dynamic Exchange of Control Parameters
Masaaki Suzuki
Department of Industrial Administration, Tokyo University of Science, Chiba, Japan

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: July 29, 2016; Accepted: September 25, 2016; Published: September 28, 2016
ABSTRACT
Updating the velocity in particle swarm optimization (PSO) consists of three terms: the inertia term, the cognitive term and the social term. The balance of these terms determines the balance of the global and local search abilities, and therefore the performance of PSO. In this work, an adaptive parallel PSO algorithm, which is based on the dynamic exchange of control parameters between adjacent swarms, has been developed. The proposed PSO algorithm enables us to adaptively optimize inertia factors, learning factors and swarm activity. By performing simulations of a search for the global minimum of a benchmark multimodal function, we have found that the proposed PSO successfully provides appropriate control parameter values, and thus good global optimization performance.
Keywords:
Swarm Intelligence, Particle Swarm Optimization, Global Optimization, Metaheuristics, Adaptive Parameter Tuning

1. Introduction
In the various aspects of optimization, there are cases where a globally optimal solution is not necessarily obtainable. In such cases, it is desirable to find instead a semi-optimal solution that can be computed within a practical timeframe. To achieve this goal, heuristic optimization techniques are popularly studied and used, typified by genetic algorithms (GA), simulated annealing (SA) and particle swarm optimization [1] (PSO). In addition, since multipoint search algorithms like GAs and PSO can determine a Pareto- optimal solution based on a one-time calculation, they are actively employed in applied research to handle multipurpose optimization problems.
If the objective function under consideration is multimodal, then heuristic optimization techniques are desired to have qualities including a global solution search ability, maintained by preservation of solution diversity; a local solution search ability, maintained conversely by centralization of the solution search; and a balance between these two. Solution diversification and centralization strategies are factors universally shared by heuristic optimization techniques, and influence their performance. However, there are few precise and universal guidelines for configuring the values of the parameters that control these strategies: their configuration is problem-specific. Additionally, tuning of these parameters is not simple, and generally requires many preliminary calculations. Furthermore, which parameter values are suitable may vary at every stage of the solution search; pertinent examples include the configuration of crossover rate and spontaneous mutation rate in GAs and the temperature cooling schedule in SA.
Focusing on PSO, a kind of multipoint search heuristic optimization technique, in this study we propose several parallel PSO algorithms in which control parameters are dynamically exchanged between a number of swarms and are adaptively adjusted during the solution search process. We also share our findings from an evaluation of algorithm performance on a minimum search problem for a multimodal objective function.
2. Particle Swarm Optimization
PSO is an evolutionary optimization calculation technique based on the concept of swarm intelligence. In PSO, the hypersurface of an objective function is searched as information is exchanged between swarms of search points, which simulate animals or insects. The next state of each individual is generated based on the optimal solution in its search history (“personal best”; pbest), the optimal solution in the combined search history of all individuals in the swarm (“global best”; gbest), and the current velocity vector. Briefly, assuming a population size Np and problem dimension Nd, the position and velocity of an individual i (where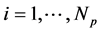 ) at the t + 1th step of the search, respectively
) at the t + 1th step of the search, respectively 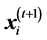 and
and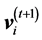 , are:
, are:
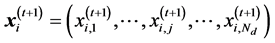 (1)
(1)
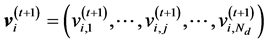 (2)
(2)
These two variables can be updated by means of the following equation, using the position and velocity at the tth step,  and
and :
:
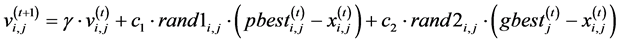 (3)
(3)
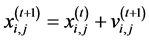 (4)
(4)
Here, 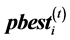 represents the optimal solution discovered during the search through the tth step by individual i itself, while
represents the optimal solution discovered during the search through the tth step by individual i itself, while 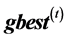 represents the optimal solution discovered during the search through the tth step by the swarm to which individual i belongs. The term
represents the optimal solution discovered during the search through the tth step by the swarm to which individual i belongs. The term 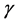 represents inertia, and takes a value between [0, 1] (inertia factor); c1 and c2 are weighting factors, respectively called the cognitive learning factor and the social learning factor (learning factors); and rand1 and rand2 are uniform random numbers in [0, 1]. The PSO solution search procedure is described below:
represents inertia, and takes a value between [0, 1] (inertia factor); c1 and c2 are weighting factors, respectively called the cognitive learning factor and the social learning factor (learning factors); and rand1 and rand2 are uniform random numbers in [0, 1]. The PSO solution search procedure is described below:
1. Decide population size and maximum number of search steps.
2. Set initial position and velocity of each individual.
3. Calculate objective function value for each individual.
4. Determine the optimal individual solution pbest for each individual and the optimal swarm solution gbest, and update these values.
5. Update the position and velocity of each individual according to Equation (3) and (4).
6. End search if desired solution accuracy is obtained or if maximum number of steps is reached.
The algorithm behind PSO is simpler than a GA, another multipoint search heuristic optimization technique, making it easier to code and tending to lead to faster solution convergence. On the other hand, PSO sometimes loses solution diversity during the search, which readily invites excessive convergence. In response, improved PSO techniques have begun to be proposed around the world. Examples include distributed PSO and hierarchical PSO, which search the solution space with multiple different swarms [2] [3] ; a method that performs a global search for its initial calculations but intensively searches the area of suboptimal solutions thereafter similar to SA [4] ; a technique that incorporates bounded rational randomness thereafter, like the “lazy ant” in ant colony optimization; and a method that avoids local solutions if the algorithm become caught in them for a while. As with many other heuristic optimization techniques, PSO includes several option control parameters that analysts can set. Because these settings can greatly influence search performance, theoretical research on stability and convergence due to parameter values [5] [6] and research and development on PSO with adaptive parameter tuning functions (e.g., [7] [8] ) are underway. The tuning of the quantum PSO (QPSO) [9] is simpler compared to standard PSO since QPSO has only a single control parameter.
3. Proposed Method
In this study, we focus on several parameters to control diversification and centralization in solution search: the inertia factor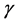 , learning factors c1 and c2, and swarm activity (described in Section 3.3). Introducing concepts similar to those employed in the replica-exchange method [10] and parallel SA method, we propose parallel PSO algorithms in which parameter values are adaptively adjusted via dynamic exchange of the above control parameters between multiple swarms during the solution search process.
, learning factors c1 and c2, and swarm activity (described in Section 3.3). Introducing concepts similar to those employed in the replica-exchange method [10] and parallel SA method, we propose parallel PSO algorithms in which parameter values are adaptively adjusted via dynamic exchange of the above control parameters between multiple swarms during the solution search process.
The replica-exchange method was developed in response to problems like spin glass and protein folding, in which it is difficult to find the ground-energy state (a global optimum solution) because several semi-stable states (local optimum solutions) exist in the system. In the replica-exchange method, several replicas of the original system are prepared, which have different temperatures and never interact with each other. We encourage readers to imagine “temperature” here as the temperature parameter in Metropolis Monte Carlo simulations, i.e., it indicates the degree to which deterioration is permitted when making the decision to transition to a candidate in the next state. Solution searches in high-temperature systems exhibit behavior close to a random search, whereas solution searches in low-temperature systems exhibit behavior close to the steepest descent method. Solution search calculations are run independently and simultaneously for each replica, each at its respective constant temperature. At the same time, temperature is exchanged periodically after a certain number of search steps according to the exchange probability w in the following equations between a given replica pair (with respective states 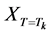 and
and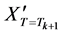 ) having adjacent temperatures (Tk and Tk+1).
) having adjacent temperatures (Tk and Tk+1).
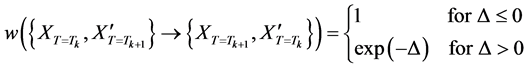 (5)
(5)
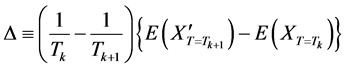 (6)
(6)
Here, E(X) represents the energy of a replica at state X (i.e., the objective function value). Figure 1 shows a schematic diagram of the replica-exchange method. In the replica-exchange method, high-temperature calculations correspond to retention of solution diversity, while low-temperature calculations correspond to a local solution search. Moreover, we can argue that it has some qualities of heuristic optimization algorithms for multimodal objective functions, in that its calculations are repeated as temperatures are probabilistically exchanged. Unlike SA, in which temperature falls monotonically, in this technique the temperature meanders if we focus on a single given replica. Thus, one can use this method to search a large solution space without becoming caught in a semi-s state.
3.1. Inertia-Factor Parallel PSO
Here, we first propose a technique focusing on the inertia factor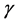 , a control parameter in Equation (3). The search trajectories of individuals with large
, a control parameter in Equation (3). The search trajectories of individuals with large 
Figure 1. Schematic illustration of the replica-exchange method, with four replicas.
whereas those of individuals with small 




Here, 


We consider Ns swarms with various different 


In IP-PSO, each swarm has its own gbest, the optimal solution found across all individuals in the swarm. Periodically, after a certain number of search steps, the objective function f(gbest) values of two swarms (





Figure 2 shows a schematic diagram of IP-PSO. The IP-PSO (and also the other proposed adaptive parallel PSOs described in Sections 3.2 - 3.4) employs the Metropolis criterion to determine the exchange acceptance of the control parameter rather than the move acceptance of each solution. The Metropolis decision will assign smaller 



Figure 2. Schematic illustration of the Inertia-factor Parallel PSO (IP-PSO), with four swarms.
cause a larger 


1. Decide total population size, number of swarms, and maximum number of search steps.
2. Assign initial inertia factor values to each swarm according to Equation (8).
3. Set initial position and velocity of each individual.
4. Calculate objective function value for each individual.
5. Determine the optimal individual solution pbest for each individual and the optimal swarm solution gbest, and update these values.
6. Update the position and velocity of each individual according to Equation (3) and (4).
7. Periodically, after a certain number of search steps, compare objective function values between two swarms having adjacent inertia factor values; make the decision to exchange inertia factors according to Equations (9) and (10).
8. End search if desired solution accuracy is obtained or if maximum number of search steps is reached.
Because each swarm can be simulated independently and simultaneously with only a slight communication cost, the IP-PSO (and also the other proposed adaptive parallel PSOs described in Sections 3.2 - 3.4) are well suited for and very efficiently runs on massively parallel computers.
3.2. Learning-Factor Parallel PSO
Here, we propose a technique focusing on learning factors c1 and c2, control parameters in Equation (3). For individuals with relatively large c1, PSO searches in the vicinity of the optimal solution in that individual’s search history, pbest, whereas for individuals with large c2, it searches in the vicinity of the optimal solution in the search history of the swarm, gbest. Thus, efficient optimization should be realizable if, in the initial search, individuals are given large c1 and small c2 values to ensure solution diversity, while in its final stages, individuals are instead given small c1 and large c2 values in an attempt to centralize the search in the vicinity of gbest. Some time-change schedules have learning factors c1 and c2 decrease (or increase) linearly with increasing number of search steps [14] .
For the Learning-factor Parallel PSO (LP-PSO) proposed in this section, we introduce the allocation parameter



Here, c0 is a constant. This paper uses c0 = 1.4955, a learning factor determined to be stable in a PSO stability analysis run by Clerc et al. [5] . When 






Thereafter, as in IP-PSO, each swarm has its own gbest, the optimal solution found across all individuals in the swarm. Periodically, after a certain number of search steps, the objective function f(gbest) values of two swarms having adjacent 









3.3. Activity Parallel PSO
Here, we propose a technique focusing on the control parameter for swarm activity. Yasuda et al. [15] used molecular motion as an analogy for the movement of each individual in PSO, and defined the activity of a swarm Act as an index of the diversification/centralization of a solution search according to the following equation:

Swarms with high activity have many individuals with high velocities, and search over a wide solution space. Swarms with low activity, on the other hand, have many individuals with low velocities, and so search intensively for local solutions. Activity is observed moment-to-moment, because searches in which activity decreases gradually and continually can yield favorable solutions. In the event that measured activity is lower than the preset baseline activity, increasing the inertia factor 
For the Activity Parallel PSO (AP-PSO) proposed in this section, we directly control swarm activity (i.e., what was measured in [15] , the past study mentioned above) in a manner similar to temperature control methods in molecular dynamics applications. Each individual’s velocity should be appropriately scaled at each search step in order to control the measured, actual activity Act (defined by Equation (13)) at the target activity Act0. Briefly, the scaling factor s is calculated according to the following equation, where the velocity vi of each individual is converted to

We consider Ns swarms controlled by various different target activity Act0 values. We determine Act0,k (

Thereafter, as in IP-PSO and LP-PSO, each swarm has its own gbest, the optimal solution found across all individuals in the population. Periodically, after a certain number of search steps, the objective function f(gbest) values of two swarms having adjacent Act0,k values are compared. Each Act0,k value is then probabilistically exchanged (or not) according to the Metropolis decisions in the same manner as Equations (9) and (10). The decision will assign smaller Act0,k value to the swarm having the superior f(gbest) value with higher probability. As a result, a more-intensive search can be performed in the vicinity of gbest. On the other hand, it is also possible to escape local optimum solutions using a global search, because larger Act0,k value is assigned to the swarm having the inferior f(gbest) value with higher-probability. Assigning an appropriate activity value to each swarm according to the search conditions makes it unnecessary to configure an activity reduction schedule in advance.
3.4. PSO with Simultaneous Exchange of Multiple Control Parameters
The proposed PSO techniques in Sections 3.1 - 3.3 above focus on only one kind of control parameter at a time, and assign parameter values that differ between each swarm. Nonetheless, adaptive control is possible if several control parameters are simultaneously and dynamically exchanged between swarms. For example, we can consider Ns swarms each having a different inertia factor 


4. Numerical Simulation and Discussion
We evaluate the performance of the proposed techniques using a minimum search problem for a Rastrigin function, a representative multimodal function. Our Rastrigin function is represented by the following equation:

The Rastrigin function is multimodal, its variables are completely independent of each other, and it has a minimum value of 



We first evaluated the proposed PSO techniques, in which only a single control parameter is exchanged in the search process. We observed the relationship between successful transitions in control parameter value and changes in objective function value, and compared its performance with other techniques. Specifically, we compared a Linearly decreasing Inertia factor PSO (LDI-PSO), in which the inertia factor linearly and continually decreases according to Equation (7) with increasing search step t, with the proposed techniques IP-PSO, LP-PSO, and AP-PSO. Table 1 shows the major simulation conditions for each technique.
Figure 3. Schematic illustration of the Inertia-factor and Activity Parallel PSO (IAP-PSO), with four swarms.
Table 1. Summary of simulation conditions for performance evaluation of the proposed PSOs which exchange a single control parameter.
Figure 4 shows time series data for the objective function f(gbest) and the control parameter values obtained via each technique. The time series shown for LDI-PSO is data for the best of eight search attempts, assuming 6400 individuals × 1 swarm. The time series shown for IP-PSO, LP-PSO, and AP-PSO are respective data for the best swarm within a representative search attempt (eight search attempts in total), assuming 800 individuals × 8 swarms. In IP-PSO, adaptive control is realized through the dynamic exchange of inertia factor values, which occurs spontaneously without the need to configure a stepwise reduction schedule for the inertia factor, a condition seen in the aforementioned [13] . Compared with LDI-PSO, which also uses the inertia factor as a control parameter and has a linear reduction schedule for the inertia factor, IP-PSO achieves lower objective function values. Looking at LP-PSO, on the other hand, small 






We next evaluated the proposed PSO techniques in which multiple parameters are exchanged simultaneously. The four techniques compared were (1) linearly decreasing inertia-factor and learning-factor PSO (LDIL-PSO), in which the inertia factor 


Figure 4. Performance evaluation of IP-PSO, LP-PSO, and AP-PSO: Time series of f(gbest) and control parameter value
the allocation parameter for learning factors 



Figure 5 shows time series plots for the objective function f(gbest) obtained via each technique. The time series shown for LDIL-PSO and LDIA-PSO are the data for the best of eight search attempts, assuming 6400 individuals × 1 swarm. The time series shown for ILP-PSO and IAP-PSO are the data for the best swarm within a representative search attempt (eight search attempts in total), assuming 800 individuals × 8 swarms. We can see that the simultaneous adjustment of multiple control parameters improves search performance compared with Figure 4. This is true if we compare those techniques in which control parameters are linearly reduced (LDI-PSO vs. LDIL-PSO, LDIA-PSO) with one another, as well as if we compare those techniques in which control parameters are dynamically exchanged (LP-PSO and AP-PSO vs. ILP-PSO and IAP-PSO). This is because the simultaneous adjustment of multiple control parameters enables each swarm to approach the equilibrium state corresponding to the parameter values at the time more rapidly. ILP-PSO and IAP-PSO yielded mean final objective function values of 2.6 and 20.6, respectively. Performance enhancement was particularly pronounced in ILP-PSO, which achieved the best objective function value of all techniques.

Figure 5. Performance evaluation of ILP-PSO and IAP-PSO: Time series of f(gbest). (a) LDIL-PSO vs. ILP-PSO; (b) LDIA-PSO vs. IAP-PSO.
Table 2. Summary of simulation conditions for performance evaluation of the proposed PSOs which exchange multiple control parameters.
5. Conclusion
We proposed five types of adaptive parallel PSO algorithms that employed the dynamic exchange of control parameters between multiple swarms-IP-PSO, LP-PSO, AP-PSO, ILP-PSO and IAP-PSO while focusing on the PSO control parameters of inertia factor, learning factors and swarm activity. The proposed algorithms were adopted to adaptively regulate control parameters at each step of the search in an experiment consisting of a minimum search problem for a multimodal function. The results show the systems transition appropriately between global and local solution search phases, meaning that efficient searches that do not stall at local optimum solutions are possible. Superior objective function values were obtained by ILP-PSO in particular: this method achieves adaptive regulation through the simultaneous exchange of the inertia factor and learning factors. Additional numerical experiments and assessments of the performance characteristics with a larger set of testing pool such as CEC benchmark are important topics for future research.
Cite this paper
Suzuki, M. (2016) Adaptive Parallel Particle Swarm Optimization Algorithm Based on Dynamic Exchange of Control Parameters. American Journal of Operations Research, 6, 401- 413. http://dx.doi.org/10.4236/ajor.2016.65037
References
- 1. Kennedy, J. and Eberhart, R.C. (1995) Particle Swarm Optimization. Proceeding of IEEE International Conference on Neural Networks, 4, 1942-1948.
http://dx.doi.org/10.1109/ICNN.1995.488968 - 2. Janson, S. and Middendorf, M. (2005) A Hierarchical Particle Swarm Optimizer and Its Adaptive Variant. IEEE Transactions on Systems, Man, and Cybernetics, Part B, 35, 1272- 1282.
http://dx.doi.org/10.1109/TSMCB.2005.850530 - 3. Yen, G.G. and Daneshyari, M. (2006) Diversity-Based Information Exchange among Multiple Swarms in Particle Swarm Optimization. Proceeding of IEEE Congress on Evolutionary Computation (CEC 2006), Vancouver, 16-21 July 2006, 6150-6157.
http://dx.doi.org/10.1109/cec.2006.1688511 - 4. Eberhart, R.C. and Shi, Y. (2000) Comparing Inertia Weights and Constrictions Factors in Particle Swarm Optimization. Proceeding of the Congress on Evolutionary Computation (CEC 2000), San Diego, 16-19 July 2000, 84-88.
http://dx.doi.org/10.1109/cec.2000.870279 - 5. Clerc, M. and Kennedy, J. (2002) The Particle Swarm: Explosion, Stability, and Convergence in a Multi-Dimensional Complex Space. IEEE Transactions on Evolutionary Computation, 6, 58-73.
http://dx.doi.org/10.1109/4235.985692 - 6. Parsopoulos, K.E. and Vrahatis, M.N. (2002) Recent Approaches to Global Optimization Problems through Particle Swarm Optimization. Natural Computing, 1, 235-306.
http://dx.doi.org/10.1023/A:1016568309421 - 7. Cooren, Y., Clerc, M. and Siarry, P. (2009) Performance Evaluation of TRIBES, an Adaptive Particle Swarm Optimization Algorithm. Swarm Intelligence, 3, 149-178.
http://dx.doi.org/10.1007/s11721-009-0026-8 - 8. Jana, N.D. and Sil, J. (2014) Particle Swarm Optimization with Lévy Flight and Adaptive Polynomial Mutation in Gbest Particle. Recent Advances in Intelligent Informatics, 235, 275-282.
http://dx.doi.org/10.1007/978-3-319-01778-5_28 - 9. Mikki, S.M. and Kishk, A.A. (2006) Quantum Particle Swarm Optimization for Electromagnetics. IEEE Transactions on Antennas and Propagation, 54, 2764-2775.
http://dx.doi.org/10.1109/TAP.2006.882165 - 10. Hukushima, K. and Nemoto, K. (1996) Exchange Monte Carlo Method and Application to Spin Glass Simulations. Journal of the Physical Society of Japan, 65, 1604-1608.
http://dx.doi.org/10.1143/JPSJ.65.1604 - 11. Shi, Y. and Eberhart, R.C. (1998) Parameter Selection in Particle Swarm Optimization, Evolutionary Programming VII. Lecture Notes in Computer Science, 1447, 591-600.
http://dx.doi.org/10.1007/BFb0040810 - 12. Li, H.-R. and Gao, Y.-L. (2009) Particle Swarm Optimization Algorithm with Exponent Decreasing Inertia Weight and Stochastic Mutation. Proceeding of 2009 2nd International Conference on Information and Computing Science, 1, 66-69.
http://dx.doi.org/10.1109/ICIC.2009.24 - 13. Xin, J., Chen, G. and Hai, Y. (2009) A Particle Swarm Optimizer with Multi-Stage Linearly-Decreasing Inertia Weight. Proceeding of the 2009 International Joint Conference on Computational Sciences, and Optimization, 1, 505-508.
http://dx.doi.org/10.1109/CSO.2009.420 - 14. Ratnaweera, A., Halgamuge, S.K. and Watson, H.C. (2004) Self-Organizing Hierarchical Particle Swarm Optimizer with Time-Varying Acceleration Coefficients. IEEE Transactions on Evolutionary Computation, 8, 240-255.
http://dx.doi.org/10.1109/TEVC.2004.826071 - 15. Yasuda, K., et al. (2008) Particle Swarm Optimization: A Numerical Stability Analysis and Parameter Adjustment Based on Swarm Activity. IEEE Transactions on Electrical and Electronic Engineering, 3, 642-659.
http://dx.doi.org/10.1002/tee.20326








