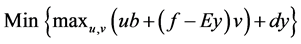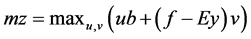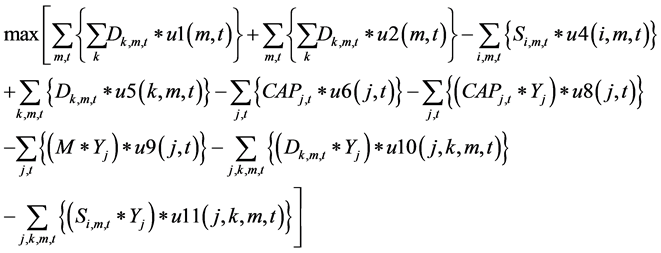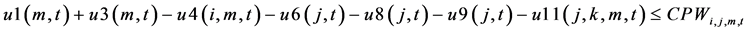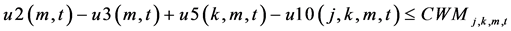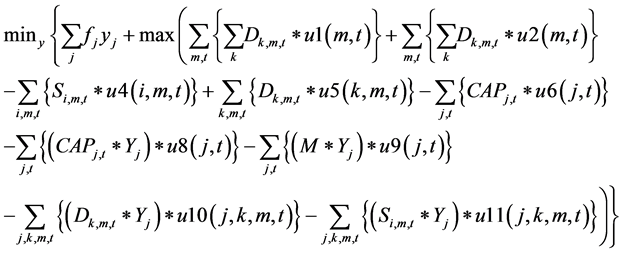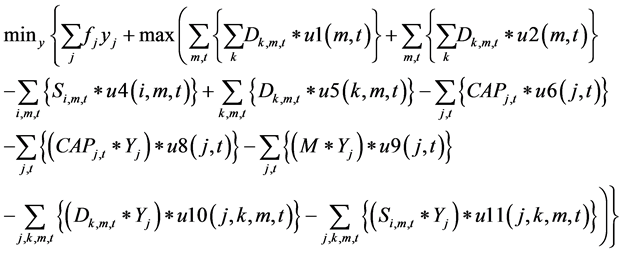American Journal of Operations Research
Vol.06 No.03(2016), Article ID:66974,15 pages
10.4236/ajor.2016.63025
Application of Modified Benders Decomposition to Single-Stage Multi-Commodity Multi-Period Warehouse Location Problem: An Empirical Investigation
Renduchintala Raghavendra Kumar Sharma1, Ankita Malviya1, Vimal Kumar1, Vinay Singh2, Pritee Agarwal3
1Department of Industrial & Management Engineering, Indian Institute of Technology, Kanpur, India
2ABV Indian Institute of Information Technology & Management, Gwalior, India
3Department of Mathematics & Statistics, Indian Institute of Technology, Kanpur, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2016; accepted 28 May 2016; published 31 May 2016
ABSTRACT
In the past, researchers have applied Bender’s decomposition to distribution problem and used feasibility constraint to speed up the performance of Bender’s decomposition. Further, the application of Branch and Bound to single-stage multi-commodity single-period warehouse location problem (SSMCSPWLP) with strong constraints has shown that they are more effective. It was also shown in the previous research (in the context of Branch and Bound Methodology) that hybrid formulation for the single-stage single-period multi-commodity warehouse location problem yielded superior results. In this paper we apply Benders’ decomposition to strong and weak formulations of single-stage multi-commodity multi-period warehouse location problem (SSMCMPWLP). As suggested in the previous literature we put feasibility constraints in the pure integer sub- problem to speed up the performance of Benders’ decomposition. We also develop an additional cut (constraint that is again added to pure integer sub-problem) and show that it further speeded up Benders’ Decomposition. This research led to the possibility of applying Benders’ Decomposition to the hybrid formulation of SSMCMPWLP in future.
Keywords:
Benders Decomposition, SSMCMPWLP, Strong and Weak Formulation, Warehouse Location, Distribution

1. Introduction and Literature Survey
Warehouse location-allocation problem is a well-known real life problem encountered in the areas like supply chain of FMCG, FCI, fertilizer, and cement distribution system etc. So, the objective of the problem is to minimize the total cost of taking the goods from the manufacturing sites to the end customers and effectiveness of strong and weak formulation. All the commodities are produced at the manufacturers’ end and directly or indirectly brought to the customer end. Large distances separate production and consumption centers, and therefore many warehouses are located at various locations between plants and markets.
Warehouse is a building constructed as a part of supply chain for the storage of goods from plants to the market. Not to store finished goods but it involves various value-added functions like consolidation, packing and shipment of orders to customers. All manufacturing facilities are not located close to market or customer so a warehouse location stage becomes essential. And thus warehouse location plays an important role in the supply chain management system. There may be more than one stage of the warehouses located between plants and the markets (multistage warehouse location problem). Consideration of minimal transportation cost and fixed cost thus is a key concern in the location allocation process of a warehouse, so transportation is done by the multi- period when the order is required. Also the capacity of the warehouse is also a matter of consideration while solving the problem. Here, we develop the strong and weak formulations for a single-stage multi-period multi- commodity warehouse location problem (SSMCMPWLP). Below the classifications of warehouse location problems researched upon are briefly described.
Single Stage/Multi-Stage
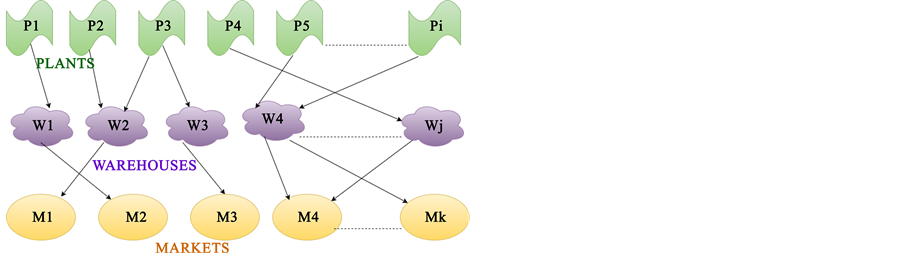
Single Stage refers to the problems where commodities are stored at a single stage between plants and markets while in the multi-stage problems commodities are stored at more than one stage. Figure 1 shows the schematic representation of single-stage multi-commodity distribution from plants to markets.
Single Period/Multi-Period
The problem which is developed for a single period ignoring the fluctuation demand and supply conditions within a period is a single-period problem whereas the multi-period problem deals with developing the problem over different periods with demand and supply fluctuating from one period to another.
Single Commodity/Multi-Commodity
When problem deals with a single commodity/product, it is a single-commodity problem otherwise multi- commodity distribution system.
Un-Capacitated/Capacitated
In un-capacitated problems the capacity of the warehouse is assumed to be infinite and in a capacitated problem it is known and fixed. However here the capacity of warehouse is a time-dependent factor as well as the demand and supply of particular time period for particular commodity are variable/dependent on previous time period and so is the capacity.
Our problem is Multi-Commodity SSCWLP, in which facility location is considered at single stage, which has been attempted by many researchers. An overview of the work done in the field of facility allocation can be looked from the review work done by ReVelle & Eiselt [1] . Geoffrion & Graves [2] , Sharma [3] , Sharma [4] and Kouvelis et al. [5] have used weak formulation of the problem and not the strong formulations. Geoffrion & Graves [2] and Sharma [3] have attempted the Single Stage SSUWLP (Single Stage Un-Capacitated Warehouse location Problem) and they have given completely different formulations considering two different real life
Figure 1. Multi-commodity distribution from plants to markets via warehouses.
problems. Keskin & Uster [6] have attempted a SSCWLP (with capacity limit at the manufacturing plant, not on the warehouse). Our problem is one where the fixed capacity of facility to be located is to be handled, i.e. CPLP. This type of problem has been attempted by various researchers in the past. The literature on CPLP as given by Francis & Goldstein [7] , Salkin [8] is abundant. This type of problem is handled and solved by researchers by both the exact solution methods and heuristic approaches. The heuristics methods used here as used for Simple Plant Location Problem (SPLP) like ADD procedure given by Kuehn and Hamburger [9] . The ADD and DROP algorithms were tested by researchers such as Khumwala [10] , Domschke & Drexl [11] and Jacobsen [12] .
Sharma [3] solved the real life fertilizer distribution system problem using Benders’ Decomposition formulating it as a mixed 0 - 1 integer linear program (MILP). The concept of strong and weak formulations as given by Sharma & Verma [13] also gave the hybrid formulations for the same problem. The proposal of multi-commod- ity problem formulation for given by Elson [14] . Capacitated plant location problem is also of interest to many researchers and many heuristic and exact approaches have been given for the same. Sharma & Agrawal [15] used vertical decomposition to solve the two staged capacitated warehouse location problem (TSCWLP) which was attempted by Keskin and Uster [6] using heuristic based scatter search algorithm. Some new strong formulations of the two staged location problem were shown by Sharma & Namdeo [16] . Sharma et al. [17] have given the strong formulations of SSSPMCWLP and shown the effectiveness of strong over weak in terms of number of iterations using Branch and Bound solutions. They also developed the hybrid formulations for it to improve the computational time.
Benders Decomposition
J.F. Benders devised an algorithm to deal with some perplexing variables i.e. those which when temporarily fixed makes the solving of the problem manageable. Benders showed that fixing the values of these variables reduces the given problem to an ordinary linear program, parameterized by the value of the perplexing variables vector. He proposed the cutting-plane algorithm for finding the optimal solution and also specifying the extreme values and set of the values of the variable fixed for which the solution remains optimal.
Bender’s decomposition is a technique to solve huge mixed-variable programming problems. It is one of the types of Decomposition methods used to solve big problem by portioning them into several sub problems. This procedure is an iterative one and when converged gives the results. The sub problem is a dual LP problem, and the master problem is a pure IP problem i.e. continuous variables are not involved. Details of Benders’ Decomposition method solving mixed 0 - 1 integer linear program can be found in Geoffrion & Graves [2] and Sharma [3] .
Geoffrion & Graves [2] concluded in their paper the remarkable effectiveness of Bender’s Decomposition as a computational study for multi commodity warehouse location problems, the numeric results showed that only a few cuts are needed to find and verify a solution within one or two tenths of one percent of the global optimum. Also a key conclusion was the choice among the mathematical representations of the same problem and incorporating one that combines the many constraints describing the convex hull of a portion of the problem’s integer feasible solutions. The major capability of this method is that how the generated cuts can be used solve the modified version of the same problem and thus the termination of the procedure can be expected to be in fewer iterations. All this was possible because of the ease in Bender’s approach which otherwise using branch & bound would not have been possible. Sharma [3] had also applied Bender’s decomposition to a distribution problem. In this feasibility constraints were included which greatly reduced the number of Bender’s iterations. Also without the feasibility constraints it was huge and cost ineffective and hence had to be terminated, the Bender’s cut once generated can be stored and used later, thus reducing the number of Bender’s iterations. Moreover, Sharma et al. [18] have proved that the Benders’ decomposition is more effective on strong formulation of SSCWLP as compared to weak formulation in terms of number of iteration and Benders’ decomposition is more effective on weak formulation of SSCWLP in terms of execution time.
2. Problem Formulation
In this research work further development in the already existing work in warehouse location problem is done, formulated and solved for single stage single period multi commodity capacitated warehouse location problem. We have made the single time period to multi time period problem and solved for multiple periods to incorporate the fluctuating demand, supply and capacity of warehouse, which is the real time case. Like in the case of Food Corporation of India (FCI) takes food grains to markets via several levels of warehousing but here we consider just a single stage warehousing however for multiple periods and making optimal use of available resources. Direct from plants to market transportation is economically is infeasible and costlier. Thus, supply chain manager’s task is the optimal distance wise and cost wise location of warehouses taking into consideration the fluctuating demand levels of various commodities market to market. For this decision making of warehouse location surveys are conducted and analysis is done by the decision makers. With each location site is associated a fixed cost and the warehouse capacity. Along with is the distance of the warehouse from plant to market called as the transportation cost per unit of commodity per commodity. The prime objective of the supply chain managers is the optimized minimization of the two costs mentioned viz. fixed cost and transportation cost, keeping into consideration the demand fulfillment and thus we get our problem SSMPMCWLP. Sharma & Verma [10] formulated SSSCUCWLP with Strong and Hybrid formulations. A similar problem (SSSPMCWLP) has been attempted by Sharma et al. [17] using weak, strong and hybrid formulations for single period only; here we solve it using weak and strong formulations for multi period using the method of Benders’ Decomposition. Here strong and weak formulations will be used for mixed integer programming problem. We will solve with these formulations using the Benders’ Partitioning algorithm and try to get best results in terms of upper bound and number of iterations so that solving large sized problems in real life could become easier. Strong linking constraints termed as strong formulations and weak linking constraints termed as weak formulations highly affect the execution time of problem as seen in previous research works. It is expected that a strong formulation gives a better result as its search area is highly reduced as compared to that of weak formulation. The major advancements in this work are the incorporation of feasibility constraint with SSMPMCWLP, an additional cut constraint and solving them by Benders’ Decomposition. So, basically this work combines the research gaps of three works. Since strong formulations take a large CPU time as shown by Sharma et al. [17] so it is expected to show similar results here also and thus it creates a path for using Hybrid formulations for the same problem. It is the amalgamation of the most efficient strong constraints with the weak constraints and the choice among which ones of strong to be added is done by simply hit and trial. Hybrid formulations carry the characteristics of both weak and strong constraints and are used to overcome the drawbacks of weak as well as strong and provide a highly effective observation in terms of number of iterations or computational time. However, we do not use the concept of hybrid formulations in this work but is of importance to have a knowledge about it as it hold the future for this research work.
Assumptions for the Problem
1) Warehouse capacity known and limited.
2) Capacity of plant for production and warehouse capacity enough to meet the market demands for different commodities at different times.
3) Storage space for each type of commodity is assumed to be same and are interchangeable, practically volume of items are different and so space required varies but this is not considered.
4) Assuming no shortage or ending inventory for any period of the problem under consideration.
5) Capacity of warehouse, demand and supply all are terms of number of units of goods.
MODEL 1: New Formulation for SSMCMPWLP
Indices Used
i: Set of the supply points (plants);
j: Set of the potential warehouse points;
k: Set of the markets;
m: Set of the commodities;
t: Set of time period from 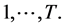
Definition of Constants
Fj: Fixed cost of establishing and maintaining the warehouse at location “j”;
Si,m,t: Supply capacity of plant “i” for commodity “m” in time period “t”;
Dk,m,t: Demand for commodity “m” at market “k” in time period “t”;
CAPj,t: Capacity of the warehouse at location “j” for all commodities (assumed that all the commodity are of same density and occupy same space in time period “t”;
M: A very large number, here taken as two times the maximum supply or maximum warehouse capacity;
CPWi,j,m: Cost of shipping one unit from plant “i” to warehouse “j” of the commodity “m”;
CWMj,k,m: Cost of shipping one unit from warehouse “j” to market “k” for commodity “m”.
Definition of Decision Variables
XPWi,j,m,t: Number of units shipped from plant “i” to warehouse “j” of the commodity type “m” in time period “t”;
XWMj,k,m,t: Number of units shipped from warehouse “j” to market “k” of commodity type “m” in time period “t”;
Yj: Binary variable which is 1 if it is decided to locate a warehouse at location “j” and 0 otherwise;
Z: Total cost of transporting commodities from plants to warehouses, warehouses to demand points or markets and fixed cost of locating the warehouses.
Problem P1
Minimize 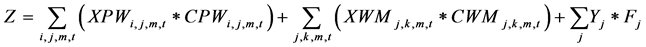 (0)
(0)
Subjected to
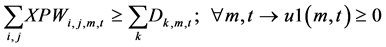 (1)
(1)
 (2)
(2)
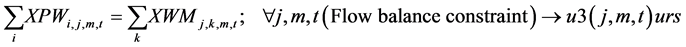 (3)
(3)
 (4)
(4)
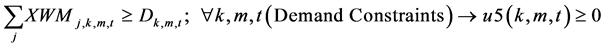 (5)
(5)
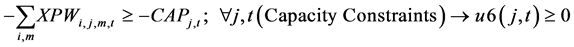 (6)
(6)
 (7a)
(7a)
 (7b)
(7b)
 (8)
(8)
 (9)
(9)
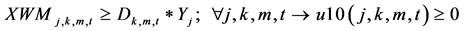 (10)
(10)
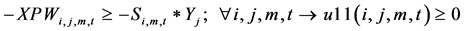 (11)
(11)
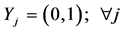
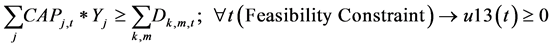
where
The objective function include the cost of transportation from plants to warehouse, the cost of transportation from warehouse to markets and the fixed cost associated with establishing a warehouse at a particular location.
The constraints 1, 2 ensures that the meeting of demand at each point or total flow equal to total demand overall. Constraints 3 - 6 are the flow balance, meeting supply, meeting demand and not overflowing the capacity of warehouse constraints respectively. Constraint 7 is non-negativity constraints. Constraint 8 is ensuring for the routing of commodity from plant to markets within the warehouse capacity. Constraint 9 is weak linking constraint. Constraint 10 is another linking constraint between demand at market to quantity shipped also ensuring locating a warehouse only when the former happens. Constraint 11 is similar to 10 just with difference of linking the shipping quantity with the supply from plant. These two are strong constraints for the problem.
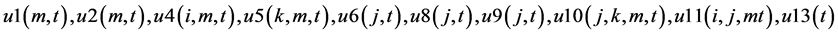
In the formulation of pure ILP feasibility constraint (Equation (13)) is also added for solving the problem as it reduced the iterations greatly as found by Sharma [3] . The following additional cut constraint was added to pure ILP. This constraint endures that same “y” vector is not returned by pure ILP problem. Here “yp” is the solution vector of previous iteration.

3. Methodology for Benders’ Decomposition
For the sake of completeness we describe the Benders’ decomposition here in brief. (Details can be seen in Sharma [3] .) The problem SSCMCMPWLP is similar to the following general mix of 0 - 1 Integer Linear Program (ILP). It is assumed that all matrices are of conformable dimensions.
Problem P
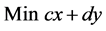
s.t

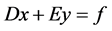
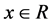
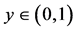
for a given “y” the problem reduces to
Problem
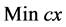
s.t
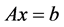
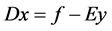
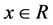
Dual of problem U_B_on_ P is: Assuming u to be dual variable of 16th and v to be dual variable of 21st equations.
Problem D_U_B_on_P

s.t
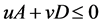

It may be noted that we begin with a “y” vector (in our work we assume that “y” will always return feasible solution to problem U_B_on_P. hence the problem D_U_B_on_P will not be and thus we have the following constraint: unbounded
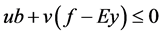
Then we solve D_U_B_on_P to set values of u and v and we are able to build a constraint (25) we substitute for D_U_B_on_P for cx in P to get
Problem P_ILP (Pure Integer Linear Program)
s.t
Equations (13) and (14)
We set
then for every extreme point (up, vp) of the D_U_B_on_P; we have
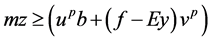
Since feasibility (13) and additional cut (14) are added to P_ILP, it ceases to give true lower bound. This is the modified Benders’ Decomposition.
It may be noted that problem D_U_B_on_P gives an upper bound on problem P. Solving D_U_B_on_P gives an additional constraint (26) for problem P_ILP, when problem P_ILP is solved then it returns additional y vector for problem D_U_B_on_P. Thus, it can be easily seen that problem P_ILP gives a lower bound on problem P. Theoretically, it will be equal to best upper bound when all cuts of type (25) are included in problem P_ILP. We thus start with a feasible “y” vector solve dual of U_B_on_P, which returns additional constraint for problem P_ILP. This entire process is termed as one iteration.
Then as P_ILP returns additional “y” vector procedure of Benders’ Decomposition is repeated.
Problem DP1
For a given value of Y dual is written as:
s.t.
Pure Integer Linear Program (ILP)
s.t.

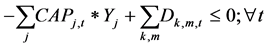
Problem DSFP1 (Dual of Strong Formulation)
s.t.
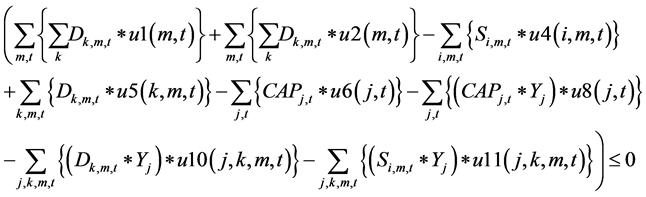
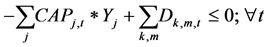
Problem DWFP1 (Dual of Weak Formulation)
s.t.
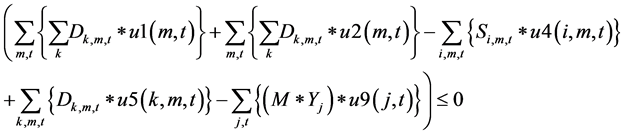

Equation (1.1) is the dual integer linear program of the problem P1 whereas Equation (2.1) is the dual integer program with the vectors linked with strong constraints of the formulation i.e. Equations (6, 8, 10, 11) and Equation (3.1) dual integer program of problem P1 with vectors linked with weak constraint Equation (9) (Big M constraint). In these the vectors linked with constraints 1, 2, 4 and 5 are neither strong nor weak but they are necessary binding constraints for the problem included in both weak and strong.
4. Empirical Investigation
In the work firstly, overall dual of problem P1 will be solved and its optimal value will thus be compared with to solve both strong (2.1) and weak (3.1) with and without the constraint 14 of additional cut as discussed above. Thus, overall this work solves and compares the following 4 models. Thus, the set of problems we setup here are:
1) Strong formulation with additional cut or Strong Twin (with feasibility constraint also);
2) Strong formulation without additional cut (with feasibility constraint also);
3) Weak formulation with additional cut or Weak Twin (with feasibility constraint also);
4) Weak formulation without additional cut (with feasibility constraint also).
As discussed above the problem instances will be created and used in solving the problem with Benders’ Decomposition for weak and strong (with or without additional cut constraint). So we define the range of values for each supply, demand, capacity and costs. The data used here may or may not match the actual real time data but our aim here is to use the same data values to solve the four set of problems and get inferences from them about the effectiveness it exhibits.
By solving the above set of problems A, B, C and D in GAMS (General Algebraic Modeling System). The concept of strong and weak constraints have developed in the context of branch and bound methodology for SSCWLP [13] [15] [18] - [20] . Sample problems were created randomly for the formulations shown for weak as well as strong of size 5 × 5 × 5 × 5 × 5, 10 × 10 × 10 × 4 × 4, 20 × 20 × 20 × 4 × 4, 30 × 30 × 30 × 4 × 4, 40 × 40 × 40 × 4 × 4 but they all seemed to be too small to show any significant difference in the time and no. of iterations required for solving the problems. Each of the problem size was tested with 25%, 50%, 100%, 200%, 300% over supply and overcapacity and results were found to be not different significantly for above four mentioned problem set up.
Thus, the need of bigger problems was felt and 50 × 50 × 50 × 4 × 4 problem showed significant results. However here also 200% over capacitated and over supply problem sets gave close values and very small but it clearly showed the effectiveness of benders decomposition method. The no. of iterations in this problem set was between 1 and 10 for at least 20 problem sets tested, when the linear programming problem required iterations in lakhs to find the optimal. The summary of results for 50 × 50 × 50 × 4 × 4 problems with 200% over capacity and 200% over supply is shown in Table 1.
We then increased the overcapacity and over supply to 400% for problem size 50 × 50 × 50 × 4 × 4 with fol-
Table 1. Results of 50 × 50 × 50 × 4 × 4 problems with 200% over capacity and 200% over supply.
lowing assumptions into consideration:
1) In each problem instance demand for each commodity in each market is taken as uniformly distributed with lower bound of 5000 units and upper bound of 7000 units.
2) The average over supply of a commodity at any plant and over capacity at any warehouse is more than the market demand at about 400%.
3) Uniform distribution of Warehouse Capacity and Supply Capacity of plants are taken.
4) Carrying cost from plant to warehouse is distributed uniformly between 1000 and 3000.
5) Carrying cost from warehouse to market is distributed uniformly between 1000 and 3000.
6) Warehouse location fi × ed cost in uniform between 800,000 and 1,000,000.
7) However, all the values in codes are taken to be in units of thousands.
Problems were created with same data input in the four categories mentioned above( A, B, C and D), all the codes were solved in GAMS using an Intel(R) Core(TM) i7-4770S CPU @ 3.10 GHz. The summary of the results for 50 × 50 × 50 × 4 × 4 problems with 400% over capacity and over supply are tabulated in given Table 2.
Table 2. Results of 50 × 50 × 50 × 4 × 4 problems with 400% over capacity and over supply.
One thing needs to be noted here that some problems had run-time greater than 24 hours and so we thereby restricted our problem size to 50 and these problem codes were terminated in 24 hours because it is practically costly and time inefficient such large computational times. Objective function values, number of iterations and CPU time for each and every problem instance is recorded and statistical analysis (t-test) is done.
The results displayed various trends:
1) Overall additional cut reduces the number of iterations in both weak and strong formulations.
・ Weak twin is better than weak without additional cut
・ Strong twin is better than strong without additional cut
2) In some problems strong twin gives lesser number of iterations than weak twin.
3) In some problems weak twin gives lesser number of iterations than strong twin.
4) In some problems strong twin gives same number of iterations as weak twin.
The results of the analysis are shown in the following tables given below (Tables 3-5).
Statistical Analysis
Hypothesis tests are conducted as follows:
1) To check whether additional cut reduces the number of iterations in both weak and strong formulations.
a) To check whether weak twin is better than weak without additional cut for a given set of problems.
μ1: Difference in means of number of iterations of weak twin and weak without additional cut
Null hypothesis, H0: μ1 = 0
Alternate hypothesis, Ha: μ1 < 0
The results of paired sample statistics for weak twin and weak without additional cut are given below in the Table 6.
From the statistical t-tables we have the critical value for t-stats at α = 0.005 as 2.668 for d.o.f. = 49 and for this t-test, t = −6.726 thus we can easily reject null hypothesis μ1 = 0.
b) To check whether strong twin is better than strong without additional cut for a given set of problems.
μ1: Difference in means of number of iterations of strong twin and strong without additional cut
Null hypothesis, H0: μ1 = 0
Alternate hypothesis, Ha: μ1 < 0
The results of paired sample statistics for strong twin and strong without additional cut are given in Table 7.
From the statistical t-tables we have the critical value for t-stats at α = 0.005 as 2.668 for d.o.f. = 49 and for this t- test, t = −49.529 thus we can easily reject null hypothesis μ1 = 0.
Table 3. Problems when strong twin gives lesser number of iterations than weak twin.
Table 4. Problems when weak twin gives lesser number of iterations than strong twin.
Table 5. Problems when weak twin gives almost same number of iterations as strong twin.
Table 6. Paired sample statistics weak twin is better than weak without additional cut.
Table 7. Paired sample statistics strong twin is better than strong without additional cut.
2) To check whether strong twin gives lesser number of iterations than weak twin in some problems.
μ1: Difference in means of number of iterations of weak twin and strong twin
Null hypothesis, H0: μ1 = 0
Alternate hypothesis, Ha: μ1 > 0
The results of paired sample statistics for strong twin and weak twin are given below in the Table 8.
From the statistical t-tables we have the critical value for t-stats at α = 0.005 as 2.845 for d.o.f. = 20 and for this t-test, t = 6.663 thus we can easily reject null hypothesis μ1 = 0.
3) To check whether weak twin gives lesser number of iterations than strong twin in some problems.
μ1: Difference in means of number of iterations of strong twin and weak twin
Null hypothesis, H0: μ1 = 0
Alternate hypothesis, Ha: μ1 < 0
The results of paired sample statistics for weak twin and strong twin are given below in the Table 9.
From the statistical t-tables we have the critical value for t-stats at α = 0.005 as 2.977 for d.o.f. = 14 and for this t-test, t = −8.091 thus we can easily reject null hypothesis μ1 = 0.
4) To check whether strong twin gives same number of iterations as weak twin in some problems.
μ1: Difference in means of number of iterations of strong twin and weak twin
Null hypothesis, H0: μ1 = 0
Alternate hypothesis, Ha: μ1 > 0
The results of paired sample statistics for strong twin and weak twin are given in the Table 10.
From the statistical t-tables we have the critical value for t-stats at α = 0.005 as 3.012 for d.o.f. = 13 and for this t-test, t = −0.280 thus we cannot reject null hypothesis μ1 = 0.
Table 8. Paired sample statistics strong twin gives lesser number of iterations than weak twin.
Table 9. Paired sample statistics weak twin gives lesser number of iterations than strong twin.
Table 10. Paired sample statistics strong twin gives same number of iterations as weak twin.
5. Results
Twin means both feasibility and additional cut constraint are put in pure integer linear program (ILP) and without means only the feasibility constraint is put in the pure ILP sub problem. We found that weak twin gave significantly better performance than weak without additional cut in terms of number of iterations and strong twin gave better performance than strong without additional cut again in terms of number of iterations. Sometimes weak twin performed better than strong twin and sometimes it was other way around. This raises the possibility of applying Benders Decomposition to hybrid formulations of SSMCSPWLP.
6. Conclusion
The results show that twin is highly effective in solving SSMCSPWLP in terms of no. of iterations; however when comparing weak twin and strong twin no definite conclusion emerges. Some problems showed weak (twin) was better and some strong (twin) was better. Thus, Benders Decomposition may be applied to a hybrid formulation of problem considered in this paper [13] .
Cite this paper
Renduchintala Raghavendra Kumar Sharma,Ankita Malviya,Vimal Kumar,Vinay Singh,Pritee Agarwal, (2016) Application of Modified Benders Decomposition to Single-Stage Multi-Commodity Multi-Period Warehouse Location Problem: An Empirical Investigation. American Journal of Operations Research,06,245-259. doi: 10.4236/ajor.2016.63025
References
- 1. ReVelle, C.S. and Eiselt, H.A. (2005) Location Analysis: A Synthesis and Survey. European Journal of Operational Research, 165, 1-19.
http://dx.doi.org/10.1016/j.ejor.2003.11.032 - 2. Geoffrion, A.M. and Graves, G.W. (1974) Multi-Commodity Distribution System Design by Bender’s Decomposition. Management Science, 20, 822-844.
http://dx.doi.org/10.1287/mnsc.20.5.822 - 3. Sharma, R.R.K. (1991) Modelling a Fertilizer Distribution System. European Journal of Operational Research, 51, 24- 34.
http://dx.doi.org/10.1016/0377-2217(91)90142-I - 4. Sharma, R.R.K. (1996) Food Grains Distribution in the Indian Context: An Operational Study. Operations Research for Development, Ahmadabad, India. Tripathy, A. and Rosenhead, J., Eds., Chapter 5, New Age International Publishers, New Delhi, 212-227.
- 5. Kouvelis, P., Rosenblatt, M.J. and Munson, C.L. (2004) A Mathematical Programming Model for Global Plant Location Problems: Analysis and Insights. IIE Transactions, 36, 127-144.
http://dx.doi.org/10.1080/07408170490245388 - 6. Keskin, B.B. and üster, H. (2007) A Scatter Search-Based Heuristic to Locate Capacitated Transhipment Points. Computers & Operations Research, 34, 3112- 3125.
http://dx.doi.org/10.1016/j.cor.2005.11.020 - 7. Francis, R.L. and Goldstein, J.M. (1974) Technical Note—Location Theory: A Selective Bibliography. Operations Research, 22, 400-410.
http://dx.doi.org/10.1287/opre.22.2.400 - 8. Salkin, H.M. and De Kluyver, C.A. (1975) The Knapsack Problem: A Survey. Naval Research Logistics Quarterly, 22, 127-144.
http://dx.doi.org/10.1002/nav.3800220110 - 9. Kuehn, A.A. and Hamburger, M.J. (1963) A Heuristic Program for Locating Warehouses. Management Science, 9, 643-666.
http://dx.doi.org/10.1287/mnsc.9.4.643 - 10. Khumawala, B.M. (1974) An Efficient Heuristic Procedure for the Capacitated Warehouse Location Problem. Naval Research logistics Quarterly, 21, 609-623.
http://dx.doi.org/10.1002/nav.3800210405 - 11. Domschke, W. and Drexl, A. (1985) ADD-Heuristics’ Starting Procedures for Capacitated Plant Location Models. European Journal of Operational Research, 21, 47-53.
http://dx.doi.org/10.1016/0377-2217(85)90086-4 - 12. Jacobsen, S.K. (1983) Heuristics for the Capacitated Plant Location Model. European Journal of Operational Research, 12, 253-261.
http://dx.doi.org/10.1016/0377-2217(83)90195-9 - 13. Sharma, R.R.K. and Verma, P. (2012) Hybrid Formulations of Single Stage Uncapacitated Warehouse Location Problem: Few Theoretical and Empirical Results. International Journal of Operations and Quantitative Management (IJOQM), 18, 53-69.
- 14. Elson, D.G. (1972) Site Location via Mixed-Integer Programming. Journal of the Operational Research Society, 23, 31-43.
http://dx.doi.org/10.1057/jors.1972.4 - 15. Sharma, R.R.K. and Agarwal, P. (2014) Approaches to Solve MID_CPLP Problem: Theoretical Framework and Empirical Investigation. American Journal of Operations Research, 4, 142-154.
http://dx.doi.org/10.4236/ajor.2014.43014 - 16. Sharma, R.R.K. and Namdeo, S. (2005) Two Stage Capacitated Warehouse Location Problem: Developing New Strong Constraints. Proceedings of Fifth International Conference on Operational Research for Development: ICORD V, Jamshedpur, 19-21 December 2005, 330-333.
- 17. Sharma, R.R.K., Tyagi, P., Kumar, V. and Jha, A. (2015) Developing Strong and Hybrid Formulation for the Single Stage Single Period Multi Commodity Warehouse Location Problem: Theoretical Framework and Empirical Investigation. American Journal of Operations Research, 5, 112-128.
http://dx.doi.org/10.4236/ajor.2015.53010 - 18. Sharma, R.R.K., Agarwal, P. and Singh, V. (2012) Bender’s Decomposition for Different Formulations of Single Stage Single Stage Capacitated Ware House Location Problem: A Brief Theoretical Framework and Empirical Investigation. International Journal of Business Research, 12, 43-50.
- 19. Sharma, R.R.K. and Berry, V. (2007) Developing New Formulations and Relaxations of Single Stage Capacitated Warehouse Location Problem (SSCWLP): Empirical Investigation for Assessing Relative Strengths and Computational Effort. European Journal of Operational Research, 177, 803-812.
http://dx.doi.org/10.1016/j.ejor.2005.11.028 - 20. Verma, P. and Sharma, R.R.K. (2011) Vertical Decomposition Approach to Solve Single Stage Capacitated Warehouse Location Problem (SSCWLP). American Journal of Operations Research, 1, 100-117.
http://dx.doi.org/10.4236/ajor.2011.13013