Received 23 November 2015; accepted 5 March 2016; published 8 March 2016

ABSTRACT

The paper investigates the powerful of hybridizing two computational intelligence methods viz., Gray Wolf Optimization (GWO) and Artificial Neural Networks (ANN) for prediction of heart disease. Gray wolf optimization is a global search method while gradient-based back propagation method is a local search one. The proposed algorithm implies the ability of ANN to find a relationship between the input and the output variables while the stochastic search ability of GWO is used for finding the initial optimal weights and biases of the ANN to reduce the probability of ANN getting stuck at local minima and slowly converging to global optimum. For evaluation purpose, the performance of hybrid model (ANN-GWO) was compared with standard back-propagation neural network (BPNN) using Root Mean Square Error (RMSE). The results demonstrate that the proposed model increases the convergence speed and the accuracy of prediction.

Keywords:

Artificial Neural Network, Gray Wolf Optimizer, Back-Propagation, Heart Disease

1. Introduction

Recently, heart problems are the major cause of deaths; human life depends on the performance of heart, which is pumping the blood to the whole parts through the body. Any heart problem will influence the other parts such as brain, kidney, lung, … etc. Many reasons will increase the risk of heart problems (diseases) such as: high or low blood pressure, smoking, high level cholesterol, obesity and lack of physical exercise. The World Health Organization (WHO) has estimated that 17.5 million deaths occur worldwide in 2012. About 7.4 million were dead based on heart disease; 6.7 million were due to stroke. As a result, heart disease is the number one cause of deaths. WHO estimated that by 2030, almost 23.6 million people will die due to heart disease [1] .

Discovering of heart disease by doctors based on symptoms, physical examinations and sings of patient body, which is hard task in the medical field. This is a multi-layered problem, which may lead to wrong presumptions and unpredictable effects. As a result, healthcare industry today develops huge amounts of complex data about patients, hospitals resources, disease diagnosis, electronic patient records, and medical devices… etc. The huge amount of data (records) is considered as key resources to be processed and analyzed for knowledge extraction that enable doctors to take the correct presumptions, which enhance the probability of survive.

In the medical field, researchers preferred to use back-propagation neural network (BPNN) to model unstructured problems due to its ability to map complex non-linear relationships between input and output variables. The back-propagation algorithm is a local search algorithm that uses gradient descent to iteratively modify the weights and biases. Minimizing the fitness function measured based on the root mean square error between the actual and ANN predicted output. Easy trapped in local minimum and slow convergence is the drawback of back-propagation algorithm. Back-propagation algorithm used to generate different set of weights and biases every re-run during training phase. As a result, each run will produce different prediction results and convergence speed.

To overcome the drawback of back-propagation algorithm, gray wolf optimizer (GWO) has been used to find the optimal starting weights and biases for back-propagation algorithm. GWO is one of the latest bio-inspired optimization algorithms, which mimic the hunting activity of gray wolves in the wildlife. GWO search for optimal solutions in different directions in order to minimize the chance of trapped in local minimum and increase the convergence speed.

The rest of the paper is organized as follows: Section 2 presents the background and literature on heart disease and Section 3 describes the methodology, in which neural networks molding of heart disease and its optimization of gray wolf optimizer through training process. Section 4 presents a discussion of the experimental results and Section 5 concludes the presented work in this paper.

2. Background

A huge number of research works have been published in the prediction area for medical field. Dilip et al. [2] applied back-propagation neural network to predict neonatal disease diagnosis. The authors applied standard back-propagation on different data-sets of neonatal disease. The accuracy of the proposed model is 75% with higher stability. Yuehjen et al. [3] proposed a several hybrid models to predict heart disease such as logistic regression (LR), multivariate adaptive regression splines (MARS), artificial neural network (ANN) and rough set (RS). The performance of the proposed models is better than artificial neural network. Humar and Novruz [4] proposed a hybrid neural network that includes artificial neural network (ANN) and fuzzy neural network (FNN) to predict diabetes and heart diseases. The proposed model is able to support good accuracy values 84.24% and 86.8% for Pima Indians diabetes data-set and Cleveland heart disease data-set, respectively.

Milan and Sunila [5] investigated several data mining algorithms to solve cardiovascular disease such as: Artificial Neural Network (ANN), Support vector Machine (SVM), Decision Tree and RIPPER classifier. The accuracy of the ANN, SVM, Decision Tree and RIPPER are 80.06%, 84.12%, 79.05% and 81.08% respectively. SVM is able to predict the cardiovascular disease with higher accuracy. Mazurowski et al. [6] investigated the performance of class imbalance in training data using neural network for medical diagnosis. Two algorithms have been used standard back-propagation (BP) and particle swarm optimization ( PSO ). The results show that BP outperforms the PSO for small and large data-sets.

Resul et al. [7] introduced a methodology which uses SAS base software 9.1.3 for predicting of the heart disease. The proposed system is developed based on neural networks. The obtained accuracy is 89.01% which is considered good enough but not optimal. Archana and Sandeep [8] introduced a novel hybrid prediction algorithm with missing value imputation (HPM-MI). The authors proposed a hybrid model based on K-means clustering with Multilayer Perceptron. The performance of the proposed algorithm is investigated on three benchmark medical data sets namely Pima Indians Diabetes, Wisconsin Breast Cancer, and Hepatitis from the UCI Repository of Machine Learning. The results are very strong and the proposed model works fine when numbers of missing value are large in the data-set. Bajaj et al. [9] applied three data mining classification algorithm for heart disease such as decision tree, split validation and apply model. The proposed system is able to reduce medical mistakes and provide high accuracy prediction. Beheshti et al. [10] proposed a new meta-heuristics approach named Centripetal Accelerated Particle Swarm Optimization (CAPSO). The proposed approach is used to enhance the performance of ANN learning and accuracy. The performance has been evaluated over nine standard medical data-sets and the results are promising. Interested readers can find more related work on [11] - [13] .

3. Methodology

This section gives a detailed account of the basic ANN and GWO, followed by a discussion on the ANN-GWO.

3.1. Artificial Neural Network

Artificial Neural Network (ANN) is adopted from the biological complex system, the human brain, which consists of a huge number of highly connected elements called neurons. ANN tries to find the relationships between input-output data pairs. In general, the collected data were randomized and split into three groups; Training (70% of the data-set), Validation and Testing (30% of the data-set) data-sets. The training data-sets used to learn the ANN based on finding the relationship between input and out pairs by adjusting the weights and biases using back-propagation algorithm. However; through learning process, there is a probability of the neural network to over-fit or over-learn the input-output data-set. This problem will generate a weak mapping between input-output especially for unseen data-set. Once over-fitting occurs, the validation data-set is used through learning process to guide and stop training if the validation error begins to rise. The prediction evaluation of the developed ANN model is done after finishing training phase though testing data-set [14] [15] . Artificial neural network have been successfully applied to solve hard and complex problems in the field of industry and research. A huge number of publications have proved the strength of ANN in the medical field [16] [17] .

The basic model of ANN consists of three layers, where each layer has different number of neurons. The three layers are input, hidden and output layers. All these layers are connected to each other in such a way so that each neuron in one layer is connected to all neurons in the following layer. The basic diagram for a network with a single neuron is illustrated in Figure 1.

The neurons of the input layer take the input data-set from the real environment. The input vector (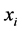) is transmitted using the connection that multiplies its strength by a weight (w) to produce the product (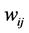). Each neuron has a biases (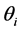). The output of the neuron is generated by 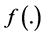and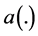, which is a summation function and activation function. An activation function consists of two algebraic formulas linear and non-linear ones. These two functions enable the neural network to find the relationships between input and output. The outputs either send to other interconnected neurons or directly to the environment. The difference between the output and neural network output is considered as error.

3.2. Gray Wolf Optimizer

Gray Wolf Optimizer (GWO) is a new bio-inspired evolutionary algorithm proposed by Seyedali et al. [18] . GWO simulates the hunting process of gray wolves in the wildlife. Wolves used to live in a pack and there are two gray wolves (male and female) managing the other wolves in the pack. A very strong social dominate hierarchy is founded inside every pack. The size of each pack usually from 5 to 12 on average. According to [18] the social hierarchy of the pack is organized as following:

1) The alphas wolves (α): The leading wolves in the pack and responsible for making decisions. The alphas orders are dictated to the pack.

2) The betas wolves (β): The second level wolves after alphas in the pack. The main job of betas wolves to help and support alphas decisions.

3) The deltas wolves (δ): The third level in the pack is delta wolves. They used to follow alpha and beta wolves. The delta wolves have 5 categories as following:

a) Scouts: wolves are used to control and monitor the boundaries of the territory and alert the pack in case of danger.

b) Sentinels: protect and guarantee the safety of the pack.

c) Elders: strong wolves used to be alpha or beta wolves in the future.

d) Hunters: wolves used to help alpha and beta though hunting prey and providing food the pack.

e) Caretakers: wolves are responsible for caring the ill, wounded and weak wolves.

4) The omegas wolves (ω): are the lowest levels in the pack and they have to follow alpha, beta and delta wolves. They are the last wolves that are allowed to eat.

GWO algorithm consider alpha (α) wolves are the fittest solution inside the pack, while the second and third best solutions are named Beta (β) and delta (δ) respectively. The result of solutions inside the pack (population) are considered omega (ω). The process of hunting a prey is guided by α, β and ω.

The first step of hunting a prey is circling it by α, β and ω. The mathematical model of circling process as shown in equations 1, 2, 3 and 4.

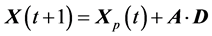(1)

where 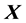is the gray wolf position. t is the number of iteration. 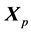is prey position and is evaluated from Equation 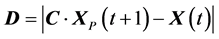(2).

(2)

the A and C are coefficient vectors are evaluated based on Equations (3) and (4) respectively.

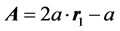(3)

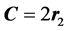(4)

where a is a linearly decreased from 2 to 0 through the number of iterations, which is used to control the tradeoff between exploration and exploitation. Equation (5) used to update the value of variable a, where NumIter is the total number of iterations. Two random vectors between [0,1] namely 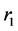and 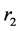to simulate hunting a prey (find the optimal solution). The solutions alpha, beta and delta are considered to have a good knowledge about the potential location of prey. These three solutions helps others wolves (omega) to update their positions according to the position of alpha, beta and delta. Equation 6 presents the formula of updating wolves’ positions.

(5)

(6)

The values of x₁, X₂ and x₃ is evaluated as in Equations (7) (8) and (9) respectively.

(7)

(8)

(9)

The x₁, X₂ and x₃ are the best 3 solutions in the population at iteration t. The values of A₁, A₂ andA₃ are evaluated in Equation (3). The values of, and are evaluated as shown in Equations (10) (11) and (12) respectively.

(10)

(11)

(12)

The values of C₁, C₂ andC₃ is evaluated in Equation (4). The pseudo code for GWO is shown in Figure 2.

3.2. Gray Wolf Optimizer of Neural Networks (ANN-GWO)

To find an accurate ANN model and reduce the drawback of back-propagation algorithm, GWO is hybridized with ANN. The proposed idea consists of two major steps. In the first one, ANN is trained using GWO. GWO is used to find the optimal initial weight and biases. The second step involves training the neural network using back-propagation algorithm. The weights and biases evolved from GWO. This idea will enhance the performance of back-propagation to search for global optima model. The weights and biases are evaluated as a vector of variables for the proposed model. The fitness of each vector is evaluated based on the Root Mean Square Error (RMSE), which finds the error between the actual input and predicted output. Equation (13) presents the RMSE, where T_i is the target output and P_i is predicted value from ANN. A lower value of RMSE indicates a better model. Figure 3 illustrates the pseudo code of the hybrid ANN-GWO algorithm.

(13)

4. Experimental Results

In the experiments, the proposed ANN-GWO is implemented using MATLAB and simulation are performed on an Intel Pentium 4, 2.33 GHz computer. We execute 11 independent runs on the data-set.

4.1. Problem Description

In this work, the data-set is adopted from UCI Machine Learning Repository, Cleveland database [19] which is a medical data-set related to heart disease. Cleveland database used to classify person into four classes (Normal (0), First Stroke (1), Second Stroke (2) and End of life (3)) regarding to the heart disease. The data-set has 166

records with 13 attributes (inputs) for each record and 4 classes (outputs). Table 1 and Table 2 illustrate the benchmark data-set and classes respectively.

4.2. Tuning Parameters for ANN and GWO

To find an accurate ANN model, a good parameters setting should be used for training and testing the ANN model. GWO is used to search for the initial optimal weights and biases. The parameters setting used for the proposed ANN-GWO after some preliminary experiments are shown in Table 3 and Table 4. GWO is able to find an optimal initial weights and biases in 51 generations, and the time used to reach optimal value of RMSE 2.812 mm was evaluated in 29.532 s. Figure 4 presents the convergence process in smooth curve with a fast decrease at the start and gradually slow down.

4.3. Results

The performance of GWO in finding the initial optimal weights and biases is founded by minimizing the RMSE (Equation (13)). The experiments for finding the initial weights and biases were implemented eleven times to ensure that RMSR reach the optimal value. In the heart disease problem, the RMSE converges to a value 2.812 mm using GWO, which is very close to 0.

In order to evaluate the performance of ANN-GWO, a comparison is done between standard ANN and ANN- GWO. Table 5 presents the results obtained for both models. The neural network architecture used for modeling ANN-GWO and standard ANN (13-8-5-2-1) is trained using back-propagation algorithm. The proposed model (ANN-GWO) is able to achieve a high quality performance goal 0.0029 in 40 epochs taking 2.435 s as shown in Figure 5. Whilst, the standard neural network based on back-propagation algorithm took 3000 epochs and 73.43 s to reach the 0.0019 goal as shown in Figure 6.

4.4. Discussions

The performance of ANN-GWO in tracking the original and predicted output for training and testing data-set is illustrated in Figure 7 and Figure 8 respectively. Analyzing the results shows that the performance of standard ANN is easy to trap in local minima and slow convergence. Whilst, ANN-GWO is faster convergence and reach optimal values better than the standard ANN. Figure 7 and Figure 8 show the values of the original and predicted results of the ANN-GWO and standard ANN respectively. It is clear that the performance of ANN-GWO is much better than standard ANN.

Figure 9 and Figure 10 show the box plots that illustrate the distribution results of the ANN-GWO and standard ANN respectively. It is clear that the ANN-GWO reduces gab between the best, average, and worst prediction

qualities, which shows that the proposed method is robust and mush better than the standard ANN. We believe that this since gray wolf optimizer helps the back-propagation to overcome the drawback of standard ANN.

5. Conclusion

This work has proposed a new hybrid algorithm between artificial neural network and gray wolf optimizer to enhance the performance of back-propagation algorithm and overcome the drawback of stuck at local minima. Based on the results of this work, GWO helps ANN to find optimal initial weights and biases, which speed up the convergence speed and reduce the RMSE error. The proposed hybrid model uses GWO as a global search algorithm, while back-propagation as a local search one. This kind of hybridization makes a balance between exploration and exploitation. Moreover, ANN-GWO model in comparison with standard back-propagation ANN, took almost more than the half time to find the optimal model. However, we believe that a future study is needed to investigate the optimal design of the neural network architecture such as number of hidden layers, number of neurons, transfer functions and learning functions.

Cite this paper

HamzaTurabieh, (2016) A Hybrid ANN-GWO Algorithm for Prediction of Heart Disease. American Journal of Operations Research,06,136-146. doi: 10.4236/ajor.2016.62016

References