American Journal of Operations Research
Vol.05 No.04(2015), Article ID:57907,4 pages
10.4236/ajor.2015.54022
On the Gas Routing via Game Theory
Irinel Dragan
University of Texas, Mathematics, Arlington, TX, USA
Email: dragan@uta.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 May 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
The delivery of the natural gas obtained by drilling, fracking and sending the product to consumers is done usually in two phases: in the first phase, the gas is collected from all wells spread on a large area, and belonging to several companies, and is sent to a depot owned by the city; then, in the second phase, another company is taking the gas on a network of ducts belonging to the city, along the streets to the neighborhoods and the individual consumers. The first phase is managed by the gas producing companies on the ducts owned by each company, possibly also on some public ducts. In this paper, we discuss only this first phase, to show why the benefits of these companies depend on the cooperation of the producers, and further, how a fair allocation of the total gas obtained, to the drilling companies, is computed. Following the model of flow games, we generate a cooperative transferable utilities game, as shown in the first section, and in this game any efficient value gives an allocation of benefits to the owners of ducts in the total network. However, it may well happen that the chosen value is not coalitional rational, in the game, that is, it does not belong to the Core of the game. By using the results obtained in an earlier work of the author, sketched in the second section, we show in the last section how the same allocation may be associated to a new game, which has the corresponding value a coalitional rational value. An example of a three person flow game shows the game generation, as well as the procedure to be used for obtaining the new game in which the same value, a Shapley Value, will give a coalitional rational allocation.
Keywords:
Cooperative TU Game, Core, Shapley Value, The Inverse Problem, Coalitional Rationality

1. The Flow Game, a Model for Gas Routing
The flow games have been introduced by E. Kalai and E. Zemel (1982), in [1] , as a class of cooperative transferable utilities games generated on a graph by means of a max-flow-min-cut algorithm. We use this model to show how this may be used for gas routing, in case that the gas extracted by several companies is sent to a common depot, while the distribution is done by a public company. An example with three companies and a graph of individual ducts belonging to each company would help in the understanding of any similar situation.
Example 1. Consider the case of a city which has wells belonging to three companies, K1, K2, K3, at the nodes A, B, C, of a graph, respectively. The companies are able to extract natural gas as follows: company K1, 11 tones at A; company K2, 13 tones at B; and company K3, 9 tones at C. The set of nodes in the graph is
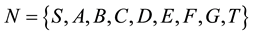 ; where S is an auxiliary common source, T is an auxiliary common sink, and the arcs are belonging to the companies as follows:
; where S is an auxiliary common source, T is an auxiliary common sink, and the arcs are belonging to the companies as follows: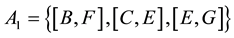 ,
,
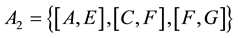 ,
,
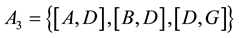 , with capacities shown in the matrix below. There is also a public duct, belonging to the city, connecting the node G to the depot node T, from which a distribution company is allocating the deliveries to customers throughout the city, on a public network. Let this arc be [G, T], with the capacity 25. We added an auxiliary node S and the auxiliary arcs [S, A], [S, B], [S, C], with capacities equal to the production power of each company, that is 11, 13, 9, respectively, for computational purposes. By inspection we easily determine that no gas producing company can send to the depot alone any amount of gas, so that if we denote the amounts provided by the singletons by
, with capacities shown in the matrix below. There is also a public duct, belonging to the city, connecting the node G to the depot node T, from which a distribution company is allocating the deliveries to customers throughout the city, on a public network. Let this arc be [G, T], with the capacity 25. We added an auxiliary node S and the auxiliary arcs [S, A], [S, B], [S, C], with capacities equal to the production power of each company, that is 11, 13, 9, respectively, for computational purposes. By inspection we easily determine that no gas producing company can send to the depot alone any amount of gas, so that if we denote the amounts provided by the singletons by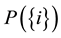 ,
,
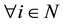 , we have
, we have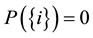 ,
,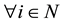 . Instead, for each pair of companies,
. Instead, for each pair of companies,
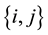 , by using all the arcs belonging to the pair
, by using all the arcs belonging to the pair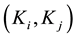 , we obtain the maximal amounts provided by the corresponding coalitions, listed as
, we obtain the maximal amounts provided by the corresponding coalitions, listed as
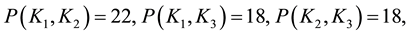
while the cooperation of all companies will give
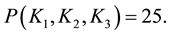
The maximal amounts for coalitions of size two are obvious from the figure; the maximal amount provided by the grand coalition should be computed in the network by a max-flow-min-cut algorithm, for example the Ford- Fulkerson algorithm (see [2] ). If there are more companies producing natural gas, the game is larger and the computation is more difficult, but the approach may be the same.
The capacities of the ducts represented by the arcs of the graph are shown in the following figure:
A graph with capacities associated to the above model.
The graph has the arcs for which there are positive capacities in the table, plus the entering and exiting auxiliary arcs, and one public arc discussed below. Now, note that the columns for S and T and the rows for G and T have been omitted, because they are empty, except a public duct, belonging to the city, [G, T], with a capacity of 25. The graph and the capacities are taken arbitrarily by the author.
As shown by the numbers that give the characteristic function of the game, the three companies should cooperate in order to get a maximum benefit. Now, the three-person cooperative TU game and any fair schedule of allocations, are obtained by using an efficient value of the game:
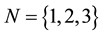
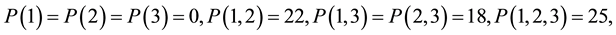
where we replaced the names of the companies by the indices and the brackets by parantheses, to keep the notation simple.
As the worth of singletons is zero, a simpler value like the Center of the Imputation Set, expressed by the formula:
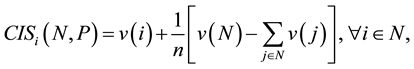
gives
which is not fair. Therefore, we shall use the Shapley Value, given by the formula:
which has more properties due to its axiomatic definition (see [2] ). By using the formula, we obtain

Obviously, the Shapley Value does not belong to the Core, as
and all the other inequalities for coalitions of size two do not hold, that is the Shapley Value is not coalitional rational, even though it is efficient, as the sum of components makes 25. Of course, any pair of companies may break the grand coalition and make a two person coalition which may give more gain to each player, while the third player is left out of the deal, an unfair solution. This instability is due exactly to the fact that the solution is not coalitional rational, which could be a motivation for the present work.
To be able to give a fair allocation, we shall solve a connected problem that has been discussed in an earlier work of the author (see [3] ). To get the paper self contained we shall remind some concepts and results from the mentioned work. The new problem introduced there is: find out a new game, with the same Shapley Value, which is coalitional rational in the new game. This problem is connected to the Inverse Problem for the Shapley Value, introduced also in some work of the author (see [4] ).
2. The Inverse Problem and the Coalitional Rationality
In [4] , the Inverse Problem for the Shapley Value has been introduced and solved. For the Shapley Value the problem may be stated: let


It is well known that the set of TU games with the set of players N, forms a vector space of dimension
where the basic vectors are defined for








As mentioned above all these vectors, invented in [4] , are linearly independent, hence they form a basis; an easy exercise is to write the seven basic vectors for our example 1. Now, any game

where the coefficients are constants which may be determined from this vector equation written in scalar form. To solve the Inverse Problem we used the results:
and the linearity of the Shapley Value. By applying these results in the above expansion of
After eliminating the constants
(see [4] , Theorem 3.5).
As mentioned above, we shall be looking for a new game in the Inverse Set relative to the Shapley Value L, which is coalitional rational. We shall confine ourselves to find such a game in the subfamily of the Inverse Set defined by all

This subset of the Inverse Set will be called the almost null subfamily. Taking into account the expressions of the basic games shown above, the games in the family given by this vector formula, may be rewritten in scalar form as

Now, the Core conditions written together give an inequality determining the values of parameter


where the minimum is taken over the index i.
The results already shown provide a procedure for solving our above stated problem:
・ Compute the Shapley Value of the given game. Check whether, or not, the Shapley Value is in the Core. If yes, stop, the problem is solved; otherwise.
・ Compute the game in the Inverse Set given by (*), for the Shapley Value L.
・ Take a value for cN in formula (*). to satisfy the inequality (**), and find out the desired game in the almost null subfamily.
Now, we intend to apply the results to the gas routing problem.
3. An Application to the Gas Routing Problem
Return to the Example 1 given in the first section, in which we associated to the network the cooperative TU game obtained by finding for each coalition the maximum flow that could be delivered by using the ducts owned by each company in the coalition and the final public arc. The TU game is
and we can compute the Shapley Value:
Obviously, this is an efficient vector, but it is not belonging to the Core, because



are not satisfied. Then, start the procedure described above, by deriving the inequality (**):
We choose the largest value of the parameter that satisfies the inequality,

where the null worth of the singletons is omitted. We obtain
Further, we can compute again the Shapley Value and find out the same vector as before. This is not only efficient, but also coalitional rational, because the Core conditions hold. A similar situation and a similar strategy may be used for the Shapley Value in the general case of games with any number of players. Moreover, the procedure will work also for any other value which is efficient. A value which is not efficient is requiring a new definition of the coalitional rational value.
The procedure may be extended to this case by using the results following from the ideas developed in the joint paper [5] , which were used in the paper [6] .
Note that the present paper is an application of the results obtained in the previous paper [3] , while for more general cases the Inverse set defined in [6] is needed.
Cite this paper
IrinelDragan, (2015) On the Gas Routing via Game Theory. American Journal of Operations Research,05,288-292. doi: 10.4236/ajor.2015.54022
References
- 1. Kalai, E. and Zemel, E. (1982) On Totally Balanced Games and Games of Flow. Mathematics of Operations Research, 7, 476-478.
http://dx.doi.org/10.1287/moor.7.3.476 - 2. Owen, G. (1995) Game Theory. 3rd Edition, Academic Press, San Diego.
- 3. Dragan, I. (2014) On the Coalitional Rationality of the Shapley Value and Other Efficient Values. American Journal of Operations Research, 4, 328-334.
http://dx.doi.org/10.4236/ajor.2014.44022 - 4. Dragan, I. (1991) The Potential Basis and the Weighted Shapley Value. Libertas Mathematica, 11, 139-146.
- 5. Dragan, I. and Martinez-Legaz, J.E. (2001) On the Semivalues and the Power Core of Cooperative TU Games. International Game Theory Review, 3, 127-139.
http://dx.doi.org/10.1142/s0219198901000324 - 6. Dragan, I. (2005) On the Inverse Problem for Semivalues of Cooperative TU Games. International Journal of Pure and Applied Mathematics, 22, 545-561.


















