American Journal of Operations Research
Vol.05 No.03(2015), Article ID:56113,16 pages
10.4236/ajor.2015.53012
A new Net Resource Factor Based Alternative Method to Calculate Revised Target in Interrupted One Day Cricket Matches
Sanjeet Singh, Arnab Adhikari
Operations Management Group, Indian Institute of Management Calcutta, Kolkata, India
Email: sanjeet@iimcal.ac.in, arnaba10@iimcal.ac.in
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 March 2015; accepted 4 May 2015; published 5 May 2015
ABSTRACT
This paper proposes an alternative method to calculate the revised target in interrupted 50 overs One Day international (ODI) cricket matches. Existing Duckworth Lewis (D/L) method and its modified versions only take available batting resources of the batting team into account and ignore the individual player’s excellence to calculate the revised target. Here, it is worth mentioning that individual player’s excellence varies in reality, and therefore quality of the available resources may affect the revised target significantly. Further in D/L method, revised target calculation depends only on the available batting resources of the batting team and does not consider the available bowling resources of the fielding team. Proposed method overcomes these two shortcomings by taking individual player’s excellence and available bowling resources of the fielding team into account. Individual player’s excellence has been determined by Data Envelopment Analysis (DEA), a well-known non parametric mathematical programming technique. A new idea of “Net Resource Factor” has been introduced to capture both batting and bowling resources to calculate the revised target. To the best of our knowledge, this is the first attempt to incorporate the ability of individual players and bowling resources of the fielding team for calculating the revised target. A comparative analysis between the proposed method and D/L method has been carried out using the data of real ODI matches held in the past. To facilitate ground application of the proposed method, a flow chart and a “Net Resource Factor Table” have been designed.
Keywords:
Decision Support Systems, Sports, Efficiency, OR, DEA, Cricket

1. Introduction
Cricket, one of the most popular team games in the world, is played in the three formats based on duration difference, i.e. a 5-day test match and two forms of limited overs cricket, viz., 50 over One Day Internationals (ODIs) and Twenty-Twenty (T-20) internationals. First version of limited over cricket format, i.e. ODI was introduced at international level in 1971. In the initial years, many ODIs were played with 40/45/55/60 overs in an innings. Finally, International Cricket Council (ICC) standardized 50 overs as a length of an innings. The first batting team sets a target for the second team with the help of 10 wickets or in maximum 50 overs whichever ends first. The second batting team has to chase the target with 10 wickets in maximum 50 overs. Sometimes, unexpected circumstances like rain, bad light, floodlight failure, etc. enforce a truncated game. As a result, the length of an innings gets shortened. In case of these shortened matches, as two teams have unequal batting and bowling resources, so a revised target is set for the second batting team. In the last two decades, International Cricket Council (ICC) adopted different methods like Average Run Rate (ARR), Most Productive Over (MPO), Discounted Most Productive Over (DMPO), PARAB, World Cup 96 (WC 96), etc.1 for calculating the revised target in the interrupted matches. Apart from these, existing literature indicates the presence of several scholarly works like VJD method [1] , Thomas method [2] , and CLARK method [3] , to calculate the revised target. But the method which is in practice and widely accepted is D/L Method [4] .
Though ARR is simplistic in nature and easy to compute, it gives stress only on the run rate and ignores the match situation. In MPO and DMPO methods, the revised target is set by excluding the first batting team’s most economic overs. As a result, they often become more biased to the first batting team because of ignoring the bowling excellence of the first fielding team. PARAB and WC96 are designed on the basis of norms’ table prepared for the overs lost. But in these two methods, numbers of wickets fallen are not considered, thus bringing down their practical significance. As per CLARK method, developed on the basis of dynamic programming model, every innings has 3 stoppages and at every stoppage, the team has different resources. The revised target is calculated on the basis of resources available. But the ambiguity among revised scores at the meeting point of two adjacent stoppages weakens this approach. Thomas [2] designed a method based on the probability of winning a match by a team before the interruption took place. But its probability conservation approach often leads to the impractical result. Jayadevan [1] also proposed another approach known as VJD method for computing the revised target in an interrupted ODI match. D/L Method is the existing method to calculate the revised target in the interrupted ODI matches. Scholars like McHale and Asif [5] concluded it as the most viable method. In the cricket world, it has gained worldwide importance because of its robustness and fairness.
However, all the resource based approaches including D/L method only focus on the batting resources of the second batting team, numbers of wickets fallen and numbers of overs remaining. Available bowling resources of the fielding team are always ignored. Here, we introduce a new idea of “Net Resource Factor” that takes both batting resources of the batting team and bowling resources of the fielding team into account. While determining available batting resources, none of these methods takes the individual player’s efficiency (quality or efficiency) into account, which differs in different players. Here, it is worthwhile to note that batting team’s capability to chase a particular target depends not only on the remaining overs and numbers of wickets lost, but also on the quality of the batsmen who are at crease and the batsmen who are yet to bat. In a similar fashion, ability of the bowling team to restrict the opponent below the target relies not only on the remaining overs, but also on the quality of the bowlers who are eligible to bowl the remaining overs. Recognizing the importance of this, the proposed method incorporates the individual excellence and remaining bowling resources of the fielding team to calculate the revised target. Here, efficiency of a player has been determined with the help of Data Envelopment Analysis (DEA), a well-known non parametric mathematical programming technique. In addition, a comparative analysis between the proposed method and D/L method has been performed using the data of real ODI matches held in the past. To the best of our knowledge, this is the first attempt to incorporate the ability of individual players and bowling resources of the fielding team for calculating the revised target.
The remainder of this paper is organized as follows. In Section 2, theoretical background and mathematical model are demonstrated. The proposed method is illustrated through a real match in Section 3. In Section 4, a comparative study between the method and the D/L method has been carried out and the implications have been demonstrated. The paper is concluded by discussing the summary of contribution and future research avenues in Section 5.
2. Theoretical Background and Model Formulation
2.1. Assumptions
Following assumptions have been used to describe the method:
1) Total batting resources and bowling resources of a team are 100 units each assuming that a team can use its resources up to 100% level in the respective batting and bowling departments.
2) In reality all batsmen and bowlers may have different capabilities. So, individual player may contribute a different percentage of resources to teams’ total resources.
3) Traditionally, there is a four years gap in the occurrence of most of the major sports events like World Cup (played in every form of game e.g. cricket, football, Hockey), Olympics etc. Following this convention of 4 year cycle, a player’s efficiency prior to any match is based on the performance of the last 4 years.
4) Since, players have different ability in terms of batting and bowling skills, all the batsmen, bowlers and all-rounders have been classified in 10 classes, i.e. 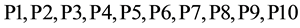 in a common “Players’ Category Table”. On the basis of efficiency scores, it is assumed that
in a common “Players’ Category Table”. On the basis of efficiency scores, it is assumed that 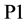 is the topmost category, P2 is the second from the top, and so on; here,
is the topmost category, P2 is the second from the top, and so on; here, 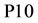 is the bottommost category. Difference of 10 units of resources has been taken between any two consecutive categories.
is the bottommost category. Difference of 10 units of resources has been taken between any two consecutive categories.
5) A player without any prior international match experience is placed in 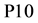 category. In a similar way, if a batsman’s batting average was less than 10 or a bowler who did not take at least five wickets in last four years is recognized as a batsman or a bowler of
category. In a similar way, if a batsman’s batting average was less than 10 or a bowler who did not take at least five wickets in last four years is recognized as a batsman or a bowler of  category. Their efficiency can take any value between 0 and 0.1. But, as international cricket demands minimum level of batting ability from all players, the highest value of efficiency of the players of
category. Their efficiency can take any value between 0 and 0.1. But, as international cricket demands minimum level of batting ability from all players, the highest value of efficiency of the players of  category has been assigned 0.099 (up to three decimal places). These thresholds help to eliminate the chance of overestimating the batting and bowling efficiency of any lower order batsman and part time bowler, respectively.
category has been assigned 0.099 (up to three decimal places). These thresholds help to eliminate the chance of overestimating the batting and bowling efficiency of any lower order batsman and part time bowler, respectively.
6) A team loses its batting or bowling resources exponentially with time due to the effect of match condition, pitch, weather, batting, bowling or fielding excellence [6] .
7) For a bowler, the resources are consumed uniformly in maximum overs a bowler can bowl in a match i.e. 10 overs in a 50 over match. If the game is shortened due to rain, then bowling resource consumption will be uniformly truncated considering the new maximum number of overs a bowler can bowl in that match.
8) If the match is stopped permanently, a bowler’s maximum over limit for computing his remaining bowling resources will be determined as per the length of the first innings. But it will maintain the aforementioned assumption of uniform consumption of bowling resources per over.
9) As it is not known when the batsman will be out, batting resource consumption on per over basis is not considered.
10) A team’s net resource factor in any match situation depends on its remaining batting resources, remaining bowling resources of the opponent team, overs to be bowled and length of the first innings.
2.2. Process Summary
Here, we have summarized the procedure to calculate the revised target. First step is to determine the efficiency of each player of two teams using DEA; categorize them as per “Players’ Category Table” and allocate resource according to the category. Second step is the computation of individual player’s contribution in team’s total batting or bowling resources. Subsequently the following information will be collected:
1) At the point of interruption, list of batsmen who got out, batsmen at the crease, batsmen yet to bat for the second batting team, and bowling summary (the overs already bowled, wickets taken and total runs conceded) of every bowler for the second fielding team.
2) In case of temporary interruption (the interruption in the second innings after which second innings resumes but the length is reduced), remaining overs left as per the revised length of the second innings.
3) In case of permanent interruption (the interruption after which match is stopped permanently), remaining overs that would have been bowled in the absence of interruption.
On the basis of this information we obtain the remaining batting resource of the second batting team and available bowling resource on the basis of individual player’s possession in team’s total batting or bowling resource and calculate the net resource factor. Finally, revised target will be calculated with the help of Net resource factor.
2.3. Player’s Quality Assessment and Resource Measurement
In this paper, individual player’s excellence has been evaluated based on the efficiency score computed using DEA. It is a nonparametric mathematical programming technique to calculate the relative efficiency of Decision Making Units (DMUs) that transform multiple inputs into multiple outputs. DEA helps to compare the efficiency of one DMU to the efficiency of other DMUs in the same peer group based on the level of the inputs used and outputs produced. These DMUs can be business units, hospitals, educational institutions, individuals etc. On the basis of Farrell’s [7] work on productive efficiency, DEA was first introduced by Charnes et al. [8] and applied in the field of engineering. Recently, many Scholars have used DEA in sports in evaluating the performance of teams or individual players. Examples of DEA application in sports include measurement of franchise efficiency in baseball [9] , measurement of the efficiency of soccer teams [10] , determination of team ranking in Olympics [11] , efficiency measurement of tennis players [12] , etc. In cricket, Singh [13] has shown the application of DEA to measure the team performance in Indian Premiere League (IPL). Amin and Sharma [14] have applied DEA to determine the efficiency of players which would be helpful to form a cricket team for the selection body.
In this work, DEA has been used to classify cricket players in different categories according to their level of efficiency. Players are considered as DMUs producing multiple outputs by taking multiple inputs. In case of batsmen, Sharp et al. [15] used batting average and strike rate as outputs whereas Amin and Sharma [14] also included highest score, number of fours and sixes as outputs in addition to aforementioned measures. But their analysis was limited to shortest version of cricket, i.e. T-20 cricket. As we are dealing with ODI cricket, to reflect the consistency of the players more effectively, total runs, number of centuries, and number of half centuries have also been used as outputs in addition to outputs used by Amin and Sharma [14] . Detailed list of input and output measures to calculate player’s efficiency is given in Table 1. For bowlers, Sharp et al. [15] and Lemmer [16] used three parameters like bowler’s economy rate, bowling average, and strike rate as outputs. Apart from these, number of wickets has been taken as additional output measure. Bowling economy rate, bowling average, and strike rate define runs conceded per over bowled, runs conceded per wicket and number of balls bowled per wicket, respectively. For batsmen, numbers of matches played by a batsman, numbers of matches he got a chance to bat, and numbers of matches where he got out have been used as inputs. For bowlers, number of matches played by a bowler and number of matches he got a chance to bowl, have been used as inputs. Following the aforementioned assumptions, a player’s efficiency prior to any match is measured in our model on the basis of performance in the last 4 years prior to the current match. Based on the efficiency score, players have been categorized into different categories and resources have been allocated as per the category, given in Table 2. Mathematically, DEA model for calculating the efficiency of any player can be described as below:
Let, there be n DMUs (here, n individual players) each having m inputs to produce s outputs. Let, 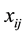 de-
de-
notes the value of the  input for the
input for the  DMU
DMU 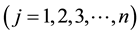 and similarly, let
and similarly, let 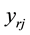 denotes the value of the
denotes the value of the 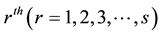 output for the
output for the  DMU
DMU . Let, the
. Let, the  being evaluated on any trial is designated as
being evaluated on any trial is designated as 





Table 1. Input and output measures to calculate player’s efficiency.
pearance of zero weights, a positive non-Archimedean infinitesimal constant 
Subject to
Based on the efficiency score
2.4. Computation of Remaining Batting Resource
After the categorization and resource allocation as per the “Players’ Category Table”, individual player’s possession in corresponding team’s total bowling and batting resources is determined. For the second batting team, remaining batting resources comprise the resources of the batsmen who are at the crease and yet to bat till the point of interruption.
2.5. Computation of Remaining Bowling Resource
Remaining bowling resources of the second fielding team depend on the overs left in each bowler’s quota and its bowling resource consumption per over. Now, determination of maximum over limit for a bowler and its bowling resource consumption per over depends on the type of interruption occurred in the match.
2.6. Method of Calculating Bowling Resource Consumption Per over for Individual Player
According to assumption (8), a bowler’s resource is uniformly consumed in the maximum overs a bowler can bowl in a match. In case of a rain interrupted match, the interruption can be either permanent or temporary. In
Table 2. Player’s category table.
case of temporary interruption, length of the second innings is shortened leading to the new maximum over limit of a bowler’s bowling quota. As a bowler can bowl less number of overs compared to an uninterrupted match, bowling resource consumption per over will be higher compared to that in case of an uninterrupted match. If a bowler does not finish the quota, some of its resource will remain unused. For example, a P1 category bowler can bowl maximum 10 overs in a 50 over match and possesses 15 units of its team’s total bowling resources. So the bowler’s bowling resource consumption per over in a full length match is 1.5 units per over or 10% of its total bowling resource per over. For the temporary interruption, if the match is shortened to 30 overs, a bowler can bowl maximum 6 overs in that match. Then the bowler’s bowling resource consumption per over is 15/6 = 2.5 units per over or 100/6 = 16.66% of his total bowling resource per over. Now, if a bowler bowls 4 overs, then 2.5 × 2 = 5 units of his bowling resource or 16.67 × 2 = 33.34% of his bowling resource will remain unused.
In case of permanent interruption, when game is not continued after the point of interruption, the maximum over limit a bowler can bowl will be decided based on the length of the first innings. Here, length of the first innings signifies the maximum over limit of the first innings for the first batting team as per the rule of the International Cricket Council (ICC). In the case of interruption in the first innings, it may be shortened from 50 overs to any specific over limit. Suppose, in a match due to the temporary interruption in first innings, length of the first innings is reduced to 45 overs. The match is stopped permanently after 30 overs of the second innings. Let, a P1 category bowler possess 18 units of his team’s total bowling resource and has already bowled 6 overs in the second innings till the point of interruption. To determine the remaining bowling resource, we consider bowling quota for a bowler same as the maximum over limit of an individual bowler in the first innings, i.e. 45/5 = 9 overs. Here, bowler’s bowling resource consumption per over will be 18/9 = 2 units per over or 100/9 = 11.11% of his total bowling resource per over. For this bowler, 2 × 3 = 6 units of his bowling resource or 11.11 × 3 = 33.33% of bowling resource will be treated as the remaining resource.
A situation may arise where the reduced length of second innings leads to the determination of unequal maximum over limit for the bowlers of second fielding team. To develop the procedure of determining the maximum over limit for individual bowler in a quantified manner, we have assumed that the captain of the second fielding team would decide the best bowlers based on the performance measures, i.e. wickets taken, the economy rate and the strike rate in the ongoing match till the point of interruption. The captain would rationally allocate the largest shares of unequal maximum bowling quotas to the best bowlers. Though in case of real match scenarios captain can call any bowler to bowl, we have assumed that the captain uses a ranking method to determine the rank of bowlers by considering number of wickets taken, the economy rate and the strike rate in the current match into account. This assumption will help to design a simplified model along with capturing the reality match. As less economy rate and strike rate is always preferred [14] , therefore weighted average of number of wickets taken, inverse of economy rate and inverse of strike rate of bowlers in that match till the point of interruption have been used to rank the bowlers, giving equal weights to all measures.
In reality, if a bowler bowled only in a few occasions in past or didn’t bowl at all, there is a very low chance that such bowler would be called to bowl. In order to eliminate the error in determining the remaining resources of these bowlers who rarely bowl, we assume that the remaining overs of these bowlers will be zero. In our method the bowlers who have not taken any wicket for the specified time span, i.e. 4 years are recognized as the bowlers of this category. The general formula to compute the bowling resource consumption per over for a bowler can be expressed as follows:
2.7. Team’s Net Resource Factor Measurement
As per assumption (10), team’s net resource factor (NRF) depends on four factors:
Team’s remaining batting resources;
Opponent team’s remaining bowling resources;
Overs to be bowled;
Length of the first innings.
Here, fundamental idea is that the batting resources of the batting team decrease exponentially with the overs. But this reduction effect is partly compensated by the exponentially decreasing bowling resources of the opponent team. So in any match situation, NRF of the batting team stands different to the conventional remaining batting resource. This NRF will be applied to Duckworth Lewis target for modifying and setting a new revised target. Here two scenarios which are illustrated below:
Scenario 1
Let, first batting team plays a certain number of overs. After that temporary interruption occurs. For this reason, its innings does not continue after that point. Now, new over limit of the innings determined for the second batting team is the length of the first innings. As the second batting team is aware of the shortened innings, it can focus on increasing the run rate from the beginning of the innings. On the other hand, first batting team may lose its opportunity to make a higher score due to sudden interruption. To get rid of the unfair advantage given to the second batting team, the NRF of the first batting team can be designated as

Scenario 2
If the permanent interruption takes place in the second innings, the NRF of the second batting team is calculated as follows:

where,


α: Remaining batting resource of the batting team;
β: Remaining bowling resource of the bowling team.
2.8. Proposed Method and Revised Target Calculation
As per D/L method, if a match is shortened or stopped permanently due to the interruption, then D/L method is used to calculate the revised target using the following equation:
where, w: wickets already lost;





Revised target of the second batting team for scenario 1 and 2 can be expressed by (3) and (4), respectively.


As per our method, if a team has less remaining batting resource compared to the remaining bowling resource of the bowling team, then it can be deduced that it has less net resource and it has to chase a higher target than the revised target set by D/L method. On the other hand, if a team has more remaining batting resource compared to the remaining bowling resource of the bowling team, then it has more net resource factor and hence revised target will be less. Thus the efforts of the batting team and bowling team up to the point of interruption of the match are recognized.
3. Numerical Illustration with a Real Match
Here, we illustrate our method with the help of a real match held between South Africa and West indies in Champions trophy 2013 played at Sophia Gardens, Cardiff, England on 14th June 2013. It was a very crucial match as the winning team would eventually qualify for the semifinal. From the beginning of the match the progress of the match had been often interrupted by rain and as a consequence, length of each innings was reduced to 31 overs. South Africa, batting first, scored 230 runs. In the second innings, the game was permanently stopped due to rain after 26・17 overs, i.e. 26 overs and 1ball. Till then West Indies scored 190 runs by losing 6 wickets. But the revised target by D/L method was 191 runs. So the match ended in tie. As South African team had the better run rate compared to West Indies in the tournament, it qualified for the next round. But, according to proposed method, the revised target would have been 189 and as a result West Indies would have emerged as winner by 1 run2. The mechanism of our proposed method is described below in details. All the data related to the input and output measures of players are collected for the 4 year span staring from 13th June 2009 to 13th June 20133. Table 3 and Table 4 represent input and output data for West Indies batsmen and South African bowlers, respectively.
Table 3. Input and output measures of West Indies batsmen.
*Denotes not out.
Table 4. Input and output measures of South African bowlers.
Using the input and output data, the efficiency of players has been determined with the help of DEAP V2.1, DEA software by Coelli [18] . Based on efficiency scores, players are categorized and resources are allocated as per players’ category table. Finally, individual resource possession in team’s total resources, i.e. 100 units is computed. As per assumption (6), players having batting average less than 10 and taking less than five wickets for batting and bowling category, respectively are assigned to P10 category. Table 5 and Table 6 demonstrate the efficiency along with classification and resource allocation of West Indies batsmen and South African bowlers, respectively. The procedure of individual resource allocation in total team’s resource is explained in detail in Appendix A.
When match stopped permanently because of rain, South African bowlers bowled 26 overs and 1 ball, i.e. 26・17 overs. Only 4・83 overs, i.e. 4 overs and 5 ball of West Indies innings were left. In an innings of 31 overs, a bowler can bowl maximum 7 overs and four bowlers can bowl maximum 6 overs each. Table 7 describes how many wickets and how much resource West Indies lost at that time, how many wickets were remaining and total batting resource left for the team till the point of interruption.
Table 5. Efficiency, classification and resource allocation of West Indies batsmen.
Table 6. Efficiency, classification, and resource allocation of South African bowlers.
Table 7. Total remaining batting resource of West Indies team till the point of interruption.
Computation procedure of remaining bowling resource for the South African team involves more complexity. Table 8 depicts the ranking method and allocation procedure of bowling quotas among the South African bowlers.
Table 9 describes the remaining overs for individual bowler, bowling resource consumption per over, and the total available bowling resources of the South Africa till the point of interruption.
Table 10 represents the revised target using proposed net resource factor based method along with the final all results obtained and statistical summary of the match.
According to our method West Indies should have won the match by 1 run and qualified for semifinal instead of South Africa.
4. Discussion
To test the effectiveness of the method, we have applied the method on four other international ODI matches where D/L method had been applied due to the interruption4. Table 11 presents a summarized comparison between revised targets and final results calculated based on the D/L method and proposed method.
Here, we have observed that the scenario 1 described in section 2.7 is similar in case of match 1 and 4 whereas scenario 2 is applicable for match number 2 and 3. From Table 11, it is evident that in the match between West Indies vs. Pakistan, proposed method gives opposite result compared to the result as per the D/L method. In the second instance, England was declared winner against India whereas our method suggests they should have chased 4 runs more in remaining 7 balls. In the rest of the cases, though the final results remain same, difference in the winning margin is quite significant from cricketing point of view.
4.1. Implication of Bowling Resource Inclusion
Inclusion of remaining bowling resource of the second fielding team in determining the revised target helps to bring forth more accurate results. In case of the first match, as second fielding team Pakistan had more available bowling resource compared to the remaining batting resource of West Indies, net resource factor of the second batting team was low. As a consequence, the revised target was set higher, compared to the target determined by D/L method. It justifies the effort of bowlers of Pakistan as they were able to keep more bowling resource on hand compared to remaining batting resource of the West Indies team till the point of interruption. Figure 1 depicts the remaining batting resource and the net resource factor of the second batting teams and available bowling
Figure 1. Remaining batting, bowling, and net resource factor.
Table 8. Bowler’s ranking and the maximum over quota for individual bowler of South African team till the point of interruption.
Table 9. Total remaining bowling resource of South African team till the point of interruption.
Table 10. Revised target calculation and match summary.
Table 11. Comparison between D/L method and proposed method.
resource of the second fielding teams these 4 matches. To see the details, readers may refer to Appendix B.
4.2. Implication of Individual Excellence Inclusion
Consideration of individual excellence is another factor that fine-tunes the revised target. Here, we have compared the available batting resource of the second batting team as per the proposed method to the available resource as per the standard edition of Duckworth-Lewis resource table7 till the point of interruption. We have found that in case of match number 1, 3, and 4 the available batting resource of the second batting team was higher as per our method compared to the D/L method where it went other way round in match number 2. Figure 2 presents this scenario. Please refer to the Appendix C to get the details of these measures.
Thus, our method recognizes the efforts of the team having more resource in hand compared to its opponent team at the point of interruption and brings more fair result. To facilitate cricket practitioners for implementation, flowchart depicted in Figure 3 has been given to determine the revised target. To get more details of Net Resource factor table, readers may refer to Appendix D.
Figure 2. Comparison between the proposed method and D/L method in determining the remaining batting resource of second batting team till the point of interruption.
Figure 3. Flowchart to calculate revised target using proposed method.
5. Conclusions and Future Research Directions
This paper presents an alternative method to calculate the revised target in interrupted ODI matches. Though Duckworth-Lewis method provides robust results at any match situation, it doesn’t take into account individual player’s excellence and importance of the second fielding team’s remaining bowling resource. Under the individual resource computation and net resource factor idea, the revised target set for the second batting team will be as fair as the effort of the team preserving more resources compared with the opponent, till the point of interruption is recognized in this method. With the example of a number of real matches where D/L method has been applied in the past, it’s shown that this method gives sensible and practical target considering all the match situations and two teams’ conditions.
As the remaining batting resource plays a crucial role in our method, it may happen that the second batting team can deliberately devise defensive batting strategy for the sake of preserving wickets. However, it is also intrinsic in the existing D/L method where captain of the second batting team can alter their batting strategy accordingly in case of probable interruption. Also, it can compel teams to devise more complex strategies of setting the batting order or bowling orders to optimize their respective resources. From future research point of view, impact of several other factors like fielding excellence and a debutante’s categorization based on his performance in domestic cricket may be taken into account.
Acknowledgements
The authors wish to express their sincere thanks to the anonymous reviewers for their insightful comments, which have significantly improved the paper.
References
- Jayadevan, V. (2002) A New Method for the Computation of Target Scores in Interrupted, Limited-Over Cricket Matches. Current Science, 83, 577-586.
- Preston, I. and Thomas, J. (2002) Rain Rules for Limited Overs Cricket and Probabilities of Victory. Journal of the Royal Statistical Society Series D (The Statistician), 51, 189-202. http://dx.doi.org/10.1111/1467-9884.00311
- Bhattacharya, R., Gill, P.S. and Swartz, T.B. (2011) Duckworth-Lewis and Twenty20 Cricket. Journal of the Operational Research Society, 62, 1951-1957. http://dx.doi.org/10.1057/jors.2010.175
- Duckworth, F.C. and Lewis, A.J. (2004) A Successful Operational Research Intervention in One-Day Cricket. Journal of the Operational Research Society, 55, 749-759. http://dx.doi.org/10.1057/palgrave.jors.2601717
- McHale, I.G. and Asif, M. (2013) A Modified Duckworth-Lewis Method for Adjusting Targets in Interrupted Limited Overs Cricket. European Journal of Operational Research, 225, 353-362. http://dx.doi.org/10.1016/j.ejor.2012.09.036
- Stern, S.E. (2009) An Adjusted Duckworth-Lewis Target in Shortened Limited Overs Cricket Matches. Journal of the Operational Research Society, 60, 236-251. http://dx.doi.org/10.1057/palgrave.jors.2602536
- Farrell, M.J. (1957) The Measurement of Productive Efficiency. Journal of the Royal Statistical Society Series A (General), 120, 253-290. http://dx.doi.org/10.2307/2343100
- Charnes, A., Cooper, W. and Rhodes, E. (1978) Measuring the Efficiency of Decision Making Units. European Journal of Operational Research, 2, 429-444. http://dx.doi.org/10.1016/0377-2217(78)90138-8
- Einolf, K.W. (2004) Is Winning Everything? A Data Envelopment Analysis of Major League Baseball and the National Football League. Journal of Sports Economics, 5, 127-151. http://dx.doi.org/10.1177/1527002503254047
- Haas, D.J. (2003) Technical Efficiency in the Major League Soccer. Journal of Sports Economics, 4, 203-215. http://dx.doi.org/10.1177/1527002503252144
- Wu, J., Zhou, Z. and Liang, L. (2010) Measuring the Performance of Nations at Beijing Summer Olympics Using Integer-Valued DEA Model. Journal of Sports Economics, 11, 549-566. http://dx.doi.org/10.1177/1527002509352619
- Ruiz, J.L., Pastor, D. and Pastor, J.T. (2011) Assessing Professional Tennis Players Using Data Envelopment Analysis (DEA). Journal of Sports Economics, 14, 276-302. http://dx.doi.org/10.1177/1527002511421952
- Singh, S. (2011) Measuring the Performance of Teams in the Indian Premier League. American Journal of Operations Research, 1, 180-184. http://dx.doi.org/10.4236/ajor.2011.13020
- Amin, G. and Sharma, S. (2014) Cricket Team Selection Using Data Envelopment Analysis. European Journal of Sport Science, 14, S369-S376. http://dx.doi.org/10.1080/17461391.2012.705333
- Sharp, G.D., Brettenny, W.J., Gonsalves, J.W., Lourens, M. and Stretch, R.A. (2011) Integer Optimisation for the Selection of a Twenty20 Cricket Team. Journal of the Operational Research Society, 62, 1688-1694. http://dx.doi.org/10.1057/jors.2010.122
- Lemmer, H.H. (2013) Team Selection after a Short Cricket Series. European Journal of Sport Science, 13, 200-206. http://dx.doi.org/10.1080/17461391.2011.587895
- Liu, F.H.F. and Hsuan Peng, H. (2008) Ranking of Units on the DEA Frontier with Common Weights. Computers and Operations Research, 35, 1624-1637. http://dx.doi.org/10.1016/j.cor.2006.09.006
- Coelli, T. (1996) A Guide to DEAP Version 2.1: A Data Envelopment Analysis (Computer) Program. CEPA Working Papers, Centre for Efficiency and Productivity Analysis, University of New England, Australia.
Appendices
Appendix A
There are 6 batsmen classified as the batsmen of P1 category, 1 batsman belongs to P2 category, 2 batsmen categorized as batsmen of P3 category and 1 from P5 and P10 each for West Indies cricket team. We have 1 bowler of P2 category, 2 bowler of P3 category, 1 bowler of P4 category, 1 bowler of P8 category and 6 bowlers of P10 category in South African cricket team. Table A1 presents individual resource allocation process of any batsman or bowler of West Indies and South Africa, respectively in detail with examples:
Table A1. Individual resource allocation computation in team’s total resource.
Appendix B
According to Figure 1 presented in Section 4.1, Table B1 describes the remaining batting resources and net resource factor of the second batting teams and remaining bowling resources of the second fielding teams for the matches discussed in Section 4.
Table B1. Remaining batting, bowling resource, and net resource factor.
Appendix C
As per Figure 2 presented in Section 4.2, Table C1 compares the remaining batting resources of second batting team till the point of interruption calculated based on the proposed method.
Table C1. Comparison between the proposed method and D/L method in determining the remaining batting resources of second batting team till the point of interruption.
Appendix D
Here, we present an excerpt of net resource factor table which facilitates the computation of net resource factor for different combination of remaining batting resource of the second batting team and remaining bowling resource of the second fielding team. Here, we present a match scenario where 10 overs are left to finish off the revised over limit of the second innings (in case of temporary interruption) or 10 overs would have been bowled (in case of permanent interruption) and length of the first innings, i.e. 30 overs. In Table D1, an excerpt of net resource factor in different remaining batting and different remaining bowling resource in the context of this example is presented.
Table D1. Net resource factor table.
NOTES
1http://cricketarchive.com/Miscellaneous/Rain_Rule_Methods.html.
2Often there may be confusion when second batting team is declared winner by a margin of runs in the interrupted matches contrary to the usual approach, i.e. number of remaining wickets in hand. As per the rule of ICC, in case of uninterrupted matches or where match continues after the interruption, i.e. temporary interruption, if the second batting team becomes winner then its winning margin is calculated by numbers of remaining wickets. When permanent interruption takes place in the second innings, i.e. match is not continued after that, if runs scored by second batting team is higher than the target computed by Duckworth Lewis method at that point of time in match, then second batting emerges as winner by the difference in second batting team’s score and target set by Duckworth Lewis method.
3http://www.espncricinfo.com/icc-champions-trophy-2013/engine/match/578622.html.
4http://www.espncricinfo.com.
5The value is obtained by using Equation (2).
6The value is obtained by using Equation (4).
7http://www.icc-cricket.com/about/38/rules-and-regulations.















