American Journal of Operations Research
Vol.4 No.2(2014), Article ID:44377,11 pages DOI:10.4236/ajor.2014.42009
Active Learning and Dynamic Pricing Policies
María-Jesús Vázquez-Gallo1, Macarena Estévez2, Santiago Egido3
1Department Civil Engineering, Technical University of Madrid, Madrid, Spain
2Conento S.L.U., Madrid, Spain
3Solute Ingenieros, San Sebastián de los Reyes, Madrid, Spain
Email: mariajesus.vazquez@upm.es, macarena.estevez@conento.com, santiago.egido@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 3 January 2014; revised 3 February 2014; accepted 10 February 2014
ABSTRACT
In this paper, we address the problem of dynamic pricing to optimize the revenue coming from the sales of a limited inventory in a finite time-horizon. A priori, the demand is assumed to be unknown. The seller must learn on the fly. We first deal with the simplest case, involving only one class of product for sale. Furthermore the general situation is considered with a finite number of product classes for sale. In particular, a case in point is the sale of tickets for events related to culture and leisure; in this case, typically the tickets are sold months before the event, thus, uncertainty over actual demand levels is a very a common occurrence. We propose a heuristic strategy of adaptive dynamic pricing, based on experience gained from the past, taking into account, for each time period, the available inventory, the time remaining to reach the horizon, and the profit made in previous periods. In the computational simulations performed, the demand is updated dynamically based on the prices being offered, as well as on the remaining time and inventory. The simulations show a significant profit over the fixed-price strategy, confirming the practical usefulness of the proposed strategy. We develop a tool allowing us to test different dynamic pricing strategies designed to fit market conditions and seller's objectives, which will facilitate data analysis and decision-making in the face of the problem of dynamic pricing.
Keywords:Dynamic Pricing; Demand Learning; Revenue Management

1. Introduction
The problem we want to solve consists in the following: for instance, suppose that someone is selling tickets for a concert to be held in a few months and trying to optimize as much as possible the benefits to be obtained. It is unknown how potential buyers will behave, both as regards the number of tickets they will buy as well as the moment when they will make their purchase. It is a question of finding a strategy enabling sellers to fine-tune prices over time, according to the sales already made, so as to increase their profits with respect to the fixed-price strategy. How do we do that?
This kind of problem is typically related to dynamic pricing, in the context of revenue management, which airlines started to apply around the 80’s of the 20th century. The challenge becomes how to offer the right product, to the right customer, at the right time, and at the right price. Usually, this requires a thorough knowledge of the complex behavior of the relevant market as in Talluri & van Ryzin [1] .
With regard to pricing, there are studies that establish reasonable assumptions about customer demand in order to develop strategies designed to optimize the expected revenue, showing how price should be allocated based on a number of factors such as the rate at which buyers reach the seller’s firm, the price they would be willing to pay and the length of the sales period. In the now classic study by Gallego and van Ryzin [2] prospective buyers arrive, according to a Poisson process, with an exponentially distributed reservation price—the price at which they would be willing to buy.
In these studies, a static model of demand is often used, requiring adequate characterization, a task which can be problematic in practice. The approach used implicitly assumes that the model is an accurate representation of the actual demand and that the model parameters can be calibrated properly using actual data, as in Bertsimas and Perakis [3] , Cope [4] , Lobo and Boyd [5] . But this does not often happen: in fact, the models are usually simplified to make them manageable, and rarely adequate actual data are available to calibrate them.
At other times, one uses a nonparametric approach in which it is only assumed that the demand function belongs to a certain class of functions sufficiently regular, but this usually involves a rapid loss of the problem tractability, as in Gallego and van Ryzin [6] , Besbes and Zeevi [7] .
It is therefore appropriate to think about strategies capable of learning from the past, with the potential to improve profits by adapting the model dynamically during the selling period, when one already has relevant information about actual demand as in Aviv and Pazgal [8] , Araman and Caldentey [9] , Lin [10] , Narahari et al. [11] .
In this regard, the main contributions of this paper are as follows:
• the development and implementation of an algorithm of dynamic pricing, without a priori information about demand, capable of learning from the past using a heuristic strategy, enabling benefits to go up from the sale of a limited inventory with different types of products in a finite-time horizon, as compared to what a fixed-price allocation would entail.
• the development and implementation of an algorithm that can dynamically establish demand for each period, depending on the prices being offered, as well on the remaining time and inventory, in order to get more realistic computational simulations.
• the development of the move© tool which, combining both algorithms will allow us to test different pricing strategies to fit market conditions and seller’s objectives, facilitating data analysis and decision-making in the face of the problem of dynamic pricing.
In what follows, Section 2 identifies the specific formulation of the problem. Section 3 describes the dynamic pricing strategies, drawing a clear distinction between the simple case, with only one product, and the multiple one, involving several products. Section 4 is devoted to the dynamic simulation of demand. Section 5 discusses in detail the computational simulations performed and the obtained results. Finally, in Section 6, some conclusions and future work lines are presented.
2. Problem formulation
In this paper, we first consider the problem faced by a seller that has some units of a certain class of products and wants to adjust prices dynamically over a finite time, in order to improve his total profit in that period with respect to a fixed-price allocation, without accurate information over the demand for this class of products, but with the possibility of learning from what happened in the past.
As a matter of fact, the actual demand can be observed over time, but the demand curve, i.e. the functional relationship between price and average demand rate that governs the observations, is unknown.
The typical product consists of tickets for an event that are being offered for sale over a certain period of time.
In the second place, we generalize the problem to the case of various classes of products. This would correspond to considering the sale of tickets for different showings of the same event, for example a theater play, as well as selling different types of tickets for the same event or show.
In both cases, the sales time interval  is divided into
is divided into 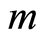 subintervals of equal length
subintervals of equal length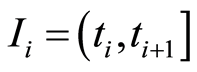 , the sales periods, where
, the sales periods, where ;
; 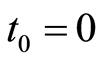 and
and . The problem translates into assigning a price
. The problem translates into assigning a price 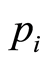 to each time interval
to each time interval  using available information about the sales process carried out up to that moment.
using available information about the sales process carried out up to that moment.
The initial price 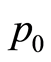 and the minimum and maximum prices that the product can reach are assumed to be determined a priori.
and the minimum and maximum prices that the product can reach are assumed to be determined a priori.
In what follows, cost is assumed to be fixed and negligible with respect to revenue, a very common situation in electronic commerce and, therefore, profit and revenue are used as synonyms.
The usual approach to this problem is to determine the optimal pricing strategy by solving equations of the Hamilton-Jacobi-Bellman type, provided that suitable hypotheses about demand are formulated, which in practice are not always satisfied; see Farias and van Roy [12] .
In this paper, aiming to increase the applicability of results to actual cases, we propose a heuristic strategy of dynamic pricing entailing a clear advantage over the fixed pricing strategy, without assuming an a priori distribution for demand. On the contrary, demand is also simulated dynamically, calculating it for each time period, based on prices being offered, along with the time and the inventory remaining. As for the initial demand, it is described in terms of a parameter, the initial interest, which allows to simulate the buyers thrust at the start of the sales period, a variable interest according to the quality of the product, the advertising campaign previous to the sales period, the media context surrounding it, and so on.
3. Pricing Strategy
We propose a heuristic strategy of dynamic pricing, whereby the price 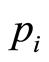 assigned to certain class of products in each time interval
assigned to certain class of products in each time interval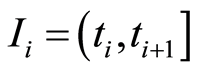 , is determined by applying a percentage increase or decrease to the price assigned in the previous period,
, is determined by applying a percentage increase or decrease to the price assigned in the previous period, . This percentage is calculated weighting a collection of factors showing the relevant information about the sale already made, allowing us to learn from past experience. Given an initial price
. This percentage is calculated weighting a collection of factors showing the relevant information about the sale already made, allowing us to learn from past experience. Given an initial price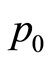 , we take
, we take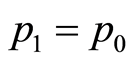 . The first update is applied to the price
. The first update is applied to the price  to calculate the new price
to calculate the new price , when you have data on at least two time intervals, in this case
, when you have data on at least two time intervals, in this case  and
and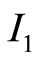 . In general, the price
. In general, the price , corresponding to interval
, corresponding to interval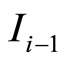 , is amended in time
, is amended in time 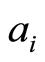 chosen randomly in this interval, giving rise to the next price
chosen randomly in this interval, giving rise to the next price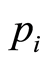 , using information gained during the intervals
, using information gained during the intervals .
.
Thus, price 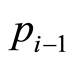 remains constant in a time interval
remains constant in a time interval 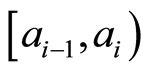 and it changes at instant
and it changes at instant , a priori unknown to potential buyers, which makes it difficult, to some extent, using adaptation strategies to respond to price variations.
, a priori unknown to potential buyers, which makes it difficult, to some extent, using adaptation strategies to respond to price variations.
The algorithm of dynamic pricing described above sets price 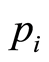 in terms of
in terms of , as:
, as:
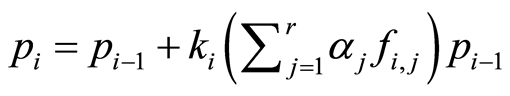 (1)
(1)
starting with  and being r the number of influencing factors over the price
and being r the number of influencing factors over the price  considered,
considered, 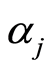 the weight assigned to factor
the weight assigned to factor 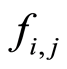 and
and 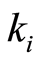 a scale factor of price variation which takes into account the time remaining to complete the sales period, see Dimicco et al. [13], namely:
a scale factor of price variation which takes into account the time remaining to complete the sales period, see Dimicco et al. [13], namely:
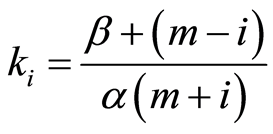 (2)
(2)
with α, the time dependence, y β the base level, parameters governing the size of the scale factor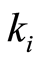 , according to the beliefs of the seller. The base level β ensures a minimum percentage change in price each time period. The value of α counter balances β to ensure that the changes in price are not too large at the beginning. It would be interesting to consider a scale factor of price variation taking into account not only the remaining time but also the remaining inventory, calibrating its size with actual data.
, according to the beliefs of the seller. The base level β ensures a minimum percentage change in price each time period. The value of α counter balances β to ensure that the changes in price are not too large at the beginning. It would be interesting to consider a scale factor of price variation taking into account not only the remaining time but also the remaining inventory, calibrating its size with actual data.
The model implemented in this algorithm is similar to the Derivative-Following strategy by Dimicco et al. [13] but with the novelty of using factors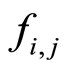 . There, the strategy adjusts its price just by looking at the amount of revenue earned on the previous day as a result of the previous day’s price change. Here the model is capable to adapt dynamically prices to increase average revenues, final revenues, recent revenues and comparative revenues, through these factors
. There, the strategy adjusts its price just by looking at the amount of revenue earned on the previous day as a result of the previous day’s price change. Here the model is capable to adapt dynamically prices to increase average revenues, final revenues, recent revenues and comparative revenues, through these factors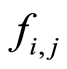 , as it is explained in next two subsections. In addition to this, weights assigned to factors allow to reflect expert’s criteria about prices.
, as it is explained in next two subsections. In addition to this, weights assigned to factors allow to reflect expert’s criteria about prices.
In the simulations performed, one can try different sets of weights  for the factors
for the factors  and compare the results obtained (see Section 5).
and compare the results obtained (see Section 5).
3.1. Simple Case
In the case of a single class of products, the percentage of increase or decrease corresponding to the price update is determined by three factors with a certain weight assigned to them, according to the formula (1).
The first factor, 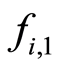 ,average revenues, reflects the relative change due to the revenue earned in the previous period with respect to the average revenue earned in the past.
,average revenues, reflects the relative change due to the revenue earned in the previous period with respect to the average revenue earned in the past.
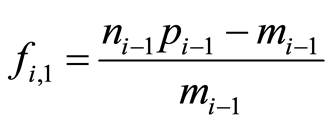
with 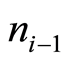 the number of units sold in the previous period
the number of units sold in the previous period ,
,  ,
,  the price corresponding to the j-th period,
the price corresponding to the j-th period, 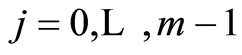 and
and  the average revenue earned up to the end of the period
the average revenue earned up to the end of the period .
.
The second factor,  , final revenues, reflects the relative variation of the trend followed by the revenue in the time since the start of the sale using dynamic pricing, with respect to the trend that would have been followed using a fixed-price strategy.
, final revenues, reflects the relative variation of the trend followed by the revenue in the time since the start of the sale using dynamic pricing, with respect to the trend that would have been followed using a fixed-price strategy.

with  the slope of the regression line corresponding to the revenues earned up to the period
the slope of the regression line corresponding to the revenues earned up to the period 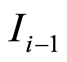 using dynamic pricing,
using dynamic pricing,  , and
, and  the slope of the regression slope corresponding to an estimate of the revenues that would have been earned up to the period
the slope of the regression slope corresponding to an estimate of the revenues that would have been earned up to the period 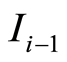 using fixed pricing.
using fixed pricing.
The third factor, 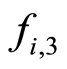 , recent revenues, reflects the relative variation due to the revenue earned in the last period,
, recent revenues, reflects the relative variation due to the revenue earned in the last period,  , with respect to the revenue earned in the previous period,
, with respect to the revenue earned in the previous period,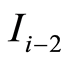 .
.

with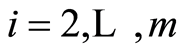 ,
,  the number of units sold corresponding to the k-th period and
the number of units sold corresponding to the k-th period and  the price corresponding to the j-th period,
the price corresponding to the j-th period, 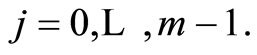
Remark: the factor  is considered to be void for revenue values appearing in the denominator close to 0.
is considered to be void for revenue values appearing in the denominator close to 0.
3.2. Multiple Case
In the case of a single class of products, the percentage of increase or decrease corresponding to the price update is determined by three factors with a certain weight assigned to them, according to the formula(1).
In the case of various classes of products, in order to update the corresponding prices a fourth factor is used which takes into account the differences between the revenues earned by the different classes of products, so that if some sort of product is earning a much higher revenue on average than the rest, its price should be risen to encourage the sale of the rest of the products and, in the opposite case, it should be lowered so as to favor its own sale.
The fourth factor,  , comparative revenues, reflects the relative variation due to the trend followed by the revenue of each class of products in the time since it started its sales with respect to the average trend of the revenue for all classes.
, comparative revenues, reflects the relative variation due to the trend followed by the revenue of each class of products in the time since it started its sales with respect to the average trend of the revenue for all classes.

where 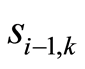 is the slope of the regression line corresponding to the k-th class, calculated using the revenues earned up to the period
is the slope of the regression line corresponding to the k-th class, calculated using the revenues earned up to the period  and
and  is the average of the slopes of the regression lines of all classes of products on sale, each of them calculated using the revenues earned from the sale of the k-th up the period
is the average of the slopes of the regression lines of all classes of products on sale, each of them calculated using the revenues earned from the sale of the k-th up the period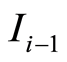 .
.
Remark: If the slope appearing in the denominator of the factor 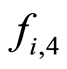 is close to 0, the factor
is close to 0, the factor 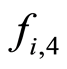 is also considered null. Moreover, in each time period and for each class of products, if there is no competition with other types of products, the weight originally associated with this factor is redistributed proportionally between the weights of the remaining factors.
is also considered null. Moreover, in each time period and for each class of products, if there is no competition with other types of products, the weight originally associated with this factor is redistributed proportionally between the weights of the remaining factors.
In computational simulations, different sets of weights for the four factors can be tested and comparisons can be made between the different results obtained (see Section 5).
This multiple case applies to the sale of tickets for events, when there are, in addition to different events, several sessions, and different types of tickets; namely, every type of product is determined by the set (event, session, ticket). Thus, for instance, the tickets of a specific type for a given session of a particular event make up a different class of products than the class formed by the tickets of another type for the same session of the same event.
4. Demand Simulation
We simulate the demand, using an algorithm that dynamically establishes demand for each period in terms of the prices being offered, as well on the remaining time and inventory.
The algorithm starts setting initial demand -understood as the number  of units sold in the first period, for each class of productsin terms of a parameter, the initial interest,
of units sold in the first period, for each class of productsin terms of a parameter, the initial interest, 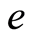 , which varies in the range
, which varies in the range 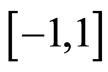 allowing us to simulate the thrust of the buyers at the start of the sales period, according to the formula:
allowing us to simulate the thrust of the buyers at the start of the sales period, according to the formula:
 (3)
(3)
In this formula, ν represents the expected proportion of fixed-price sales, which is considered as a linear function of the initial interest:
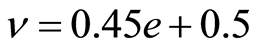 according to the opinion of experts in the field of selling tickets for events related to culture and leisure: the minimum expected sale of tickets is 5% and the maximum is 95%. The minimum (resp. maximum) sale corresponds to a case of interest −1 (resp. 1), reflecting a buyer’s perception as negative (resp. positive) as possible about the event.
according to the opinion of experts in the field of selling tickets for events related to culture and leisure: the minimum expected sale of tickets is 5% and the maximum is 95%. The minimum (resp. maximum) sale corresponds to a case of interest −1 (resp. 1), reflecting a buyer’s perception as negative (resp. positive) as possible about the event.
As for the expression , where
, where 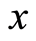 is the number of units in the initial inventory and
is the number of units in the initial inventory and 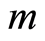 the number of sale periods, it represents the linear demand, i.e., the case where the number of units sold in each period is proportional to the elapsed time.
the number of sale periods, it represents the linear demand, i.e., the case where the number of units sold in each period is proportional to the elapsed time.
Remark: For the most negative values of the initial interest, in which the expression 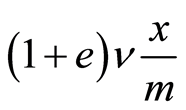 would be null or close to zero, the maximum that appears in the formula for
would be null or close to zero, the maximum that appears in the formula for  ensures that the initial number of units sold exceeds a certain level, again in accordance with actual experience in the field of ticket sales for events related to culture and leisure.
ensures that the initial number of units sold exceeds a certain level, again in accordance with actual experience in the field of ticket sales for events related to culture and leisure.
Subsequently, in each period , and for each class of product, the algorithm computes the demand, defined as the number of units sold
, and for each class of product, the algorithm computes the demand, defined as the number of units sold , applying a variation percentage over the demand in the previous period
, applying a variation percentage over the demand in the previous period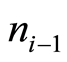 , according to the formula:
, according to the formula:

starting with 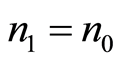 given by equation (3) and being
given by equation (3) and being  the number of influencing factors on the demand
the number of influencing factors on the demand  considered, and
considered, and  the weight assigned to the factor
the weight assigned to the factor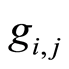 .
.
This variation percentage in demand is calculated weighting three factors, described below.
The first factor,  , remaining time, increases the variation percentage when time is running short (people who want to go to the event need to buy the tickets as soon as possible).
, remaining time, increases the variation percentage when time is running short (people who want to go to the event need to buy the tickets as soon as possible).
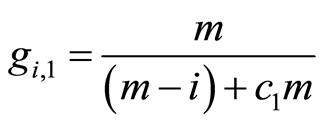
In this expression, the scale factor  takes the value 1 in the performed simulations, and it could be recalibrated with actual data on demand.
takes the value 1 in the performed simulations, and it could be recalibrated with actual data on demand.
The second factor,  , remaining inventory, increases the variation percentage when there are few remaining units of the product to sell (people who want to go to the event have to buy the tickets before they are sold out).
, remaining inventory, increases the variation percentage when there are few remaining units of the product to sell (people who want to go to the event have to buy the tickets before they are sold out).
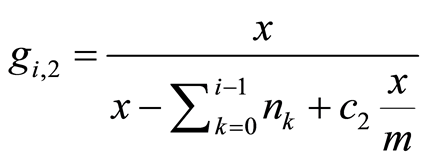
In this expression,  , is the cumulative sale up to the previous period. Again, the scale factor
, is the cumulative sale up to the previous period. Again, the scale factor 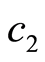
takes the value 7 in the simulations, and it could be recalibrated with actual data on demand.
The third factor, 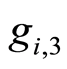 , price sensitivity, reflects the frequent occurrence in practice that sales tend to fall if the price offered at a certain time of the selling process is greater than the initial price,
, price sensitivity, reflects the frequent occurrence in practice that sales tend to fall if the price offered at a certain time of the selling process is greater than the initial price,  , and otherwise sales will tend to rise. This is expressed in terms of a parameter, the buyer’s price sensitivity,
, and otherwise sales will tend to rise. This is expressed in terms of a parameter, the buyer’s price sensitivity, 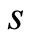 , which scales that effect, varying in the range
, which scales that effect, varying in the range  and it has been calibrated using actual sales data. The expression of the factor
and it has been calibrated using actual sales data. The expression of the factor  is:
is:
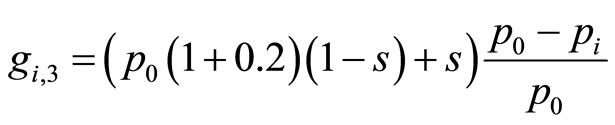
In the case of various classes of products, in future studies, a fourth factor, 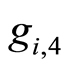 ,called competition could be tested, thereby reducing the number of units sold of a class of products where other similar class is available at a lower price, otherwise increasing the number of units sold.
,called competition could be tested, thereby reducing the number of units sold of a class of products where other similar class is available at a lower price, otherwise increasing the number of units sold.
In computational simulations, various sets of weights  can be tested, for the
can be tested, for the  factors and then the results obtained can be compared (see Section 5).
factors and then the results obtained can be compared (see Section 5).
5. Results
As for the computational simulations, the cycle that follows each simulation at a given time interval consists on calculating:
• the price that the seller will offer in that interval, adapted to what happened up to the previous time interval, as described in Section 3;
• the demand for that interval depending on the price offered, the remaining time and the remaining inventory, as described in Section 4.
• the increase in the quantities sold and the benefit earned in contrast to what would have happened with a fixed-price strategy corresponding to the expected rate of sale (with numerical and graphical information).
The input parameters are:
In the case of the seller:
 Sets of weights for the factors involved in price changes, which can be chosen according to the seller's objectives.
Sets of weights for the factors involved in price changes, which can be chosen according to the seller's objectives.
 : Sets of weights for the factors involved in the simulation of demand, which can be chosen according to the beliefs of the seller.
: Sets of weights for the factors involved in the simulation of demand, which can be chosen according to the beliefs of the seller.
 : Number of units in the initial inventory.
: Number of units in the initial inventory.
 : Length of the sales period (measured in days).
: Length of the sales period (measured in days).
 : Number of sales periods.
: Number of sales periods.
 : Initial price.
: Initial price.
In the case of the buyer:
Product: event, session, type of ticket.
Number of product units.
In the case of the selling process (demand simulation):
 : Initial interest (in the range
: Initial interest (in the range ).
).
 : Buyer’s price sensitivity (in the range
: Buyer’s price sensitivity (in the range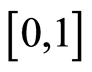 ).
).
The time intervals are of 24 hours. For instant of time at each interval it is meant 1 hour (thus, in the case of price updates made at instants randomly chosen in each time interval, it has to be noted that from each price update to the next one, a minimum of one hour and a maximum of 47 hours would elapse). Prices are expressed in cents of the currency unit (in order to appreciate subtle variations).
As for the different collections of weights considered to price updating, they are related to the factors involved in its calculation. In this way, the sets of weights  can be: balanced
can be: balanced , final and recent
, final and recent , recent and competitive
, recent and competitive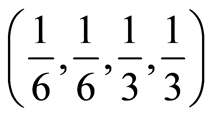 . Other sets of weights could be established to intensify or soften the impact of the various factors.
. Other sets of weights could be established to intensify or soften the impact of the various factors.
As for the different collections of weights considered to the update of the demand, they correspond to the factors involved in its calculation. Thus, the sets of weights 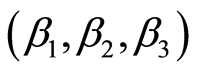 can be: balanced
can be: balanced 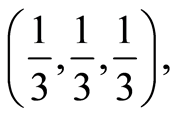 price sensitive
price sensitive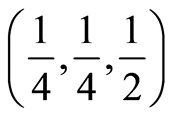 , temporal
, temporal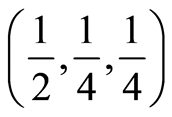 , and inventory related
, and inventory related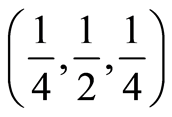 . As with the previous case, other sets of weighs could be established to intensify or soften the impact of the various factors.
. As with the previous case, other sets of weighs could be established to intensify or soften the impact of the various factors.
The computational simulations have been carried out through the move© tool, a Java application.
The graphical interface of move allows you to perform a virtual sale based on parameters describing the actions of the seller, of the buyer and the selling process. An example of this interface is shown in Figure 1.
The seller has a management window in which, in addition to editing installations and activities, he can act on some of the parameters of the model.
Regarding the parameters related to the scale of price variation (see Section 3), the time dependence is related to the time remaining to complete the sales period and the base level guarantees a minimum size of price variations. Basically, the seller does not need to act on them. Concerning the weights of the four factors influencing the dynamic calculation of price (see Subsections 3.1 and 3.2), the tool allows you to choose different distributions in accordance with the seller's beliefs. In the equiweighted case all weights are equal, but it is also possible to give more weight to some than others. For example, if the seller's priority is achieving a balance between the sales of different classes of products, the factor of comparative revenues will increase its weight and the others will see it decrease.
Similarly, one can choose several sets of weights for the three factors that influence on the dynamic simulation of the demand, according to the importance attached by the seller to the remaining time, the remaining inventory and the price sensitivity factors (see Section 4).
Respect to the demand simulation and comparison of the dynamic pricing strategy used along with that of fixed-price, the expected percentage of fixed-price sale was taken as a specific linear function of the initial interest, according to the view of experts on the field of minimum and maximum sales (see Section 4). There is no need to vary the coefficients of that linear function in the simulations.
The tool also offers the possibility of rounding the sales to whole numbers, as well as introducing random noise in the simulation of demand, which adds to the number of tickets sold in each period. This reflects the random nature of the factors that may influence future demand for the products on sale. The amplitude regulates the size of the number being added.
As regards the behavior of the parameters of the sales process, initial interest and price sensitivity, in relation to sales and revenue, the simulations confirm that:
• for fixed price sensitivity and growing interest, going from -1 to 1, sales and revenues will gradually increase, except when no grading is possible because maximum possible sales have been reached, corresponding to very high sensitivities to price, close to 1.
• for fixed interest and increasing sensitivity to price are equal, going from 0 to 1, increments in sales and revenues begin when sensitivity reaches 0.5, the average value. Until then, changes in low sensitivities, smaller than 0.5, neither significantly affect sales nor revenues for a fixed interest.
This behavior can be seen in Figure 2, which corresponds to simulation carried out for the simple case—a single class of products—with initial inventory (capacity)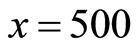 , number of sales periods
, number of sales periods , initial price
, initial price  and price range
and price range . The sets of weights used are equiweighted for factors that influence price and give priority to the time factor in relation to demand.
. The sets of weights used are equiweighted for factors that influence price and give priority to the time factor in relation to demand.
As for the comparison between the proposed strategy of dynamic pricing and that of fixed-price, which would correspond to selling at the initial price the expected sales ratio of the initial inventory, simulations confirm that for most choices of parameter pairs, the amount sold and the revenue earned is improved. The graphs below correspond to the multiple case with two classes of products for sale and different selling periods, the initial inventory (seats) is , in both cases, the number of sales periods is 10 in the first case, and 12 in the second. In both cases, the initial price is
, in both cases, the number of sales periods is 10 in the first case, and 12 in the second. In both cases, the initial price is 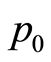 es
es  the price range is
the price range is 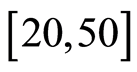 and the sets of weights used are equiweighted.
and the sets of weights used are equiweighted.
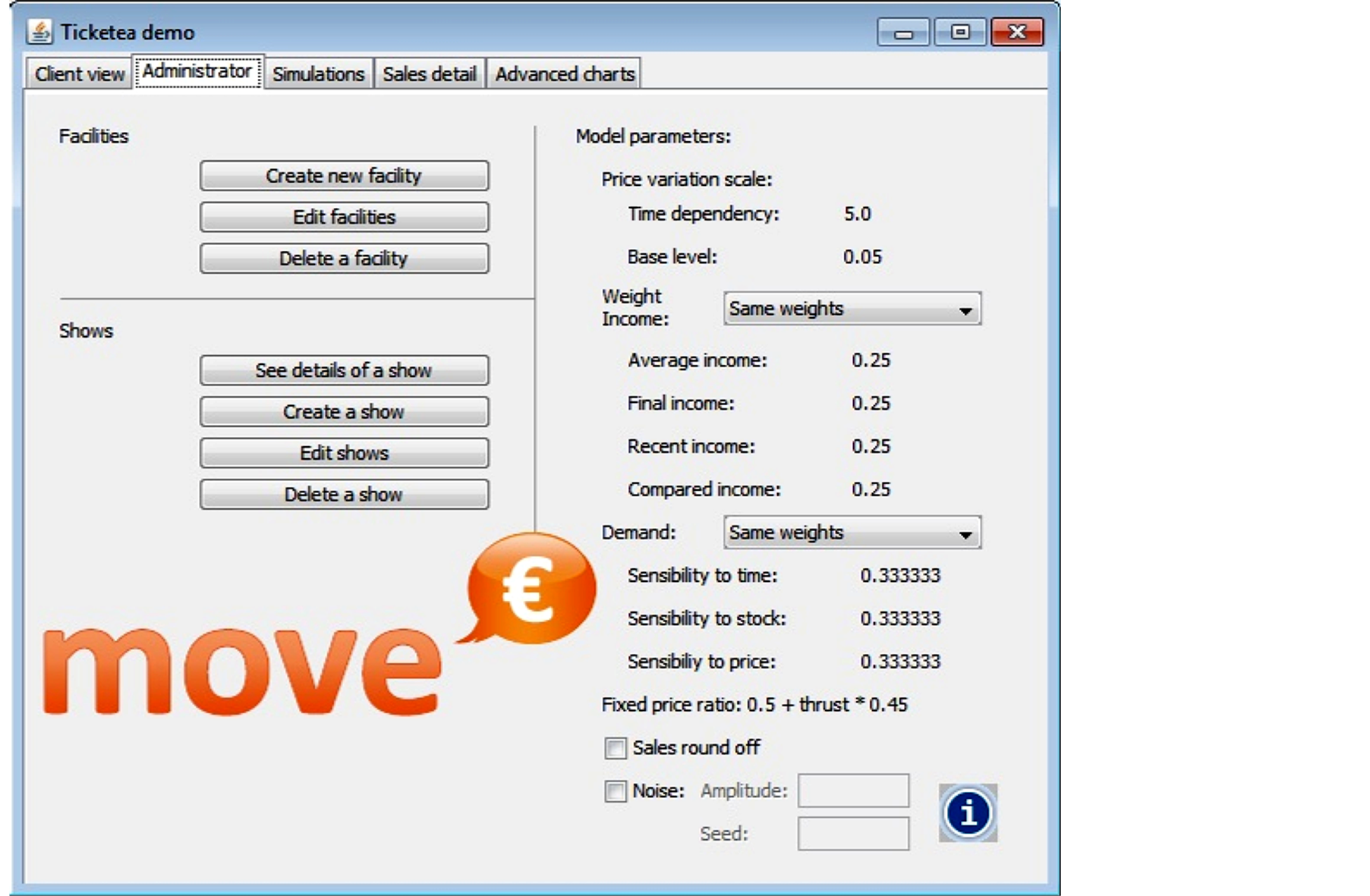
Figure 1. Graphical interface of the move© tool, a Java application.

Figure 2. Revenues vs sensitivities. simple clase equiweighted.
The graphs of revenues vs. time for interest 0 and sensitivity 0.5, show that even with no initial interest and an average sensitivity, the revenues earned, using the proposed dynamic pricing strategy (orange curves) improve with respect to the fixed-pricing strategy (blue curves) as it can be seen in Figure 3.
For zero interest and maximum sensitivity, the proposed heuristic performs particularly well reflecting the ability of the model to adjust prices dynamically to buyer’s behavior. The gain of the dynamic pricing strategy vs. the fixed one is shown in Figure 4.
For an intermediate case, with interest 0.5 and sensitivity 0.8, the gain is also clear. See Figure 5.
Even in the case where the initial interest is negative −1, and the sensitivity to price is 1, the dynamic pricing strategy is clearly more advantageous. See Figure 6.
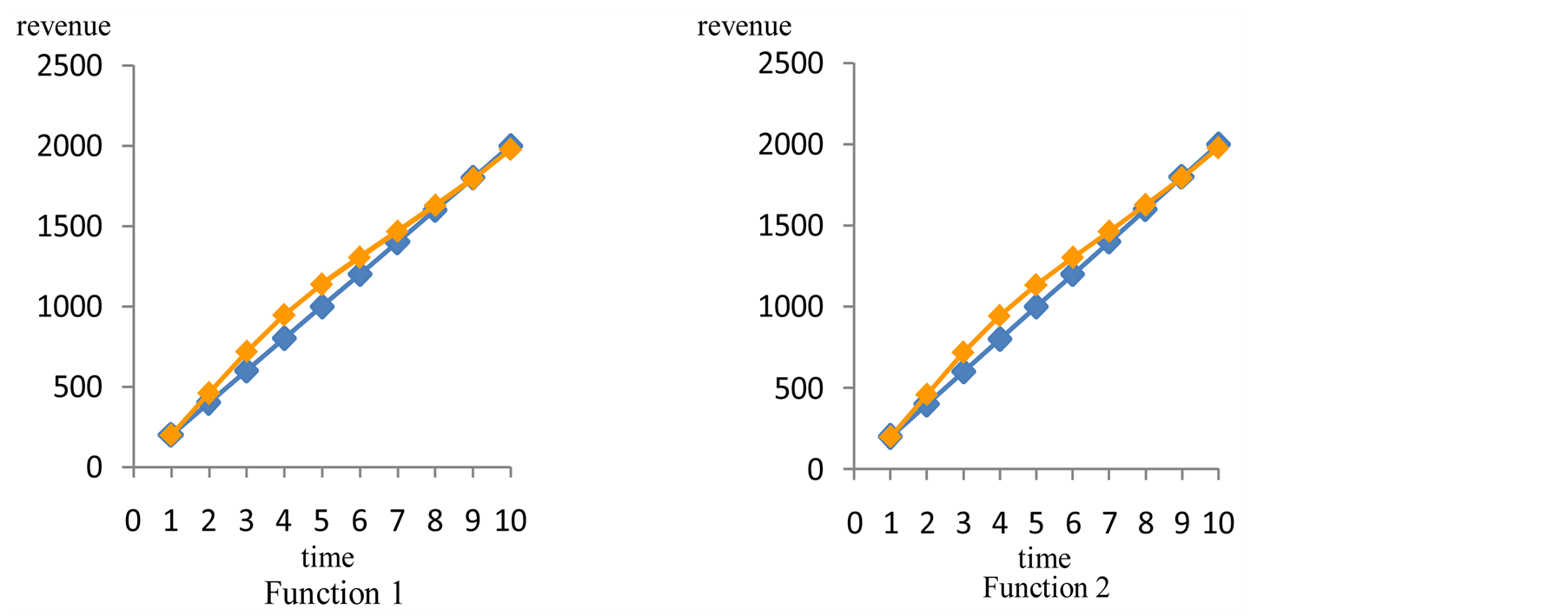
Figure 3. Revenues vs time. Multiple case: two functions on sale. Interest 0. Sensitivity 0.5.
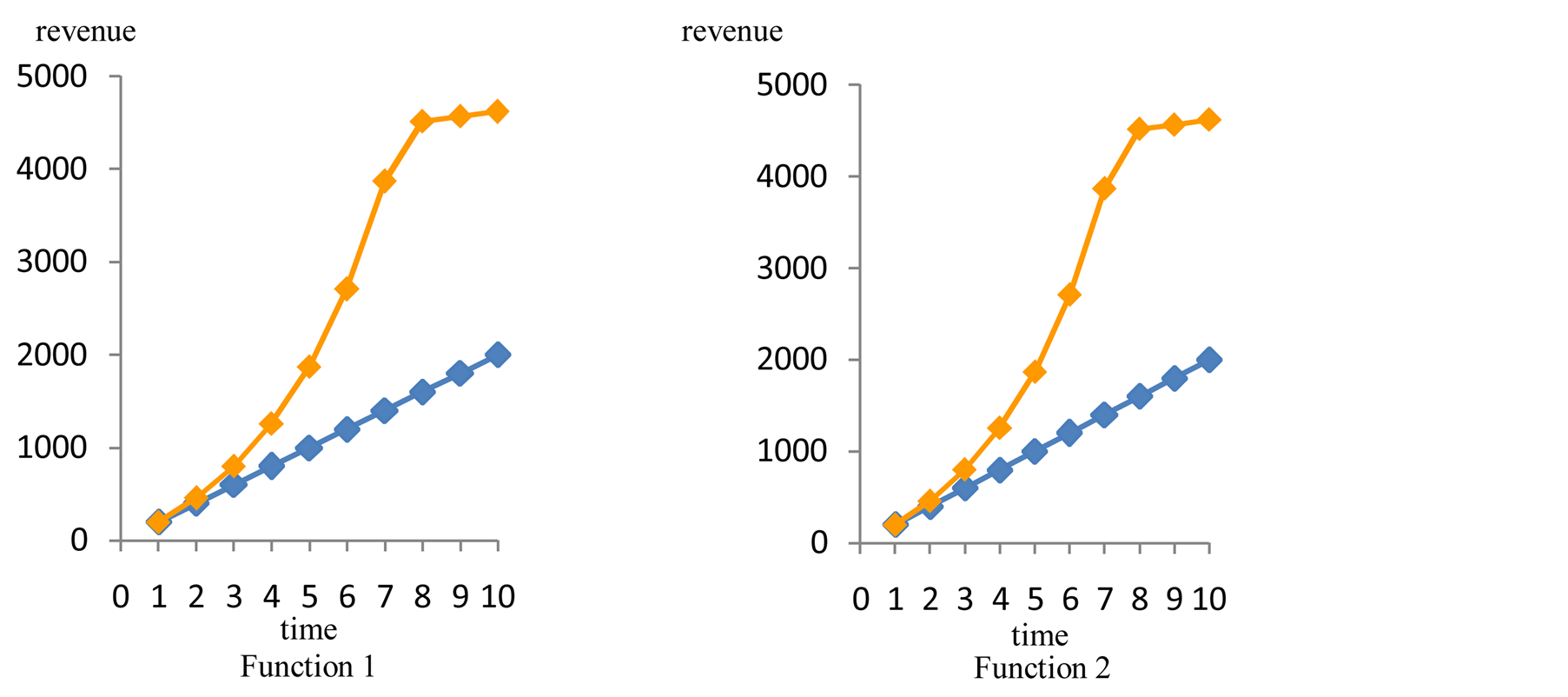
Figure 4. Revenues vs time. Multiple case: two functions on sale. Interest 0. Sensitivity 1.
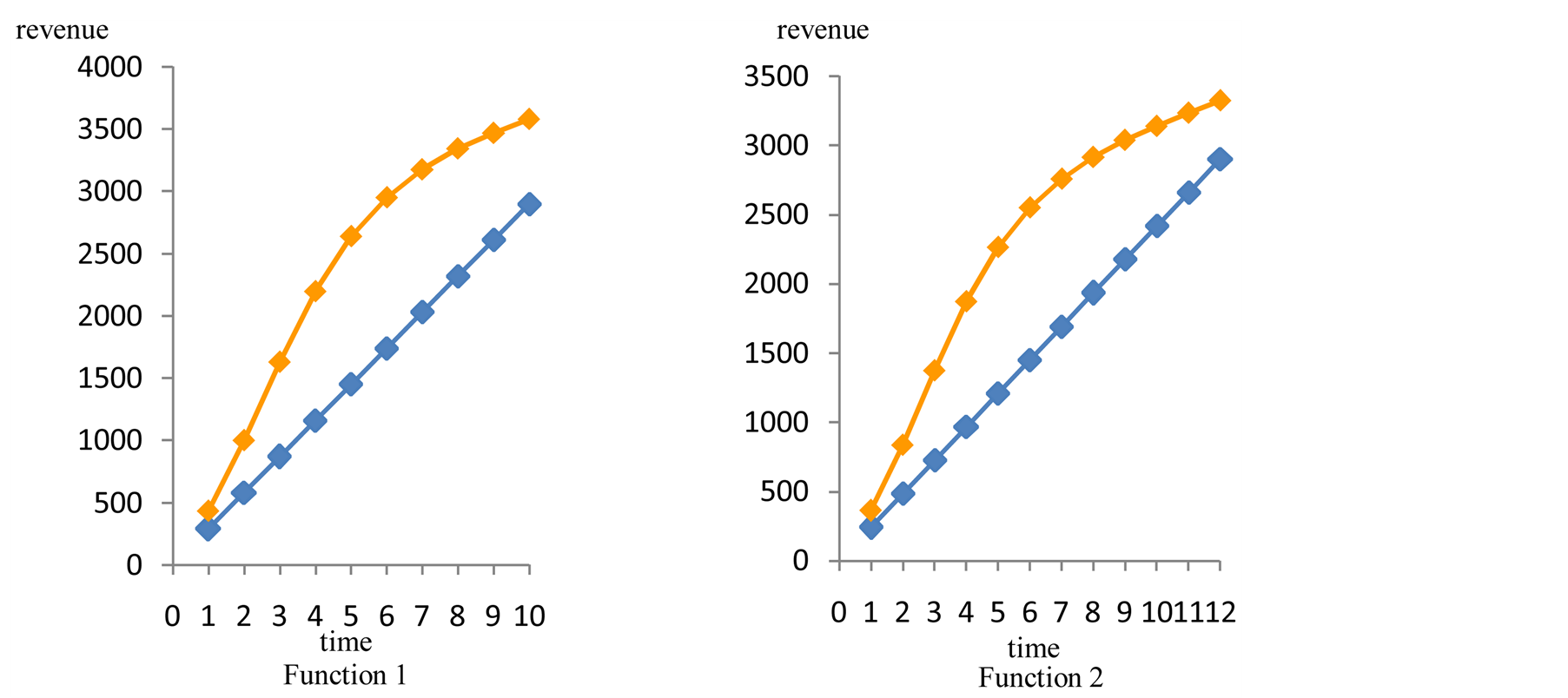
Figure 5. Revenues vs time. Multiple case: two functions on sale. Interest 0.5. Sensitivity 0.8.
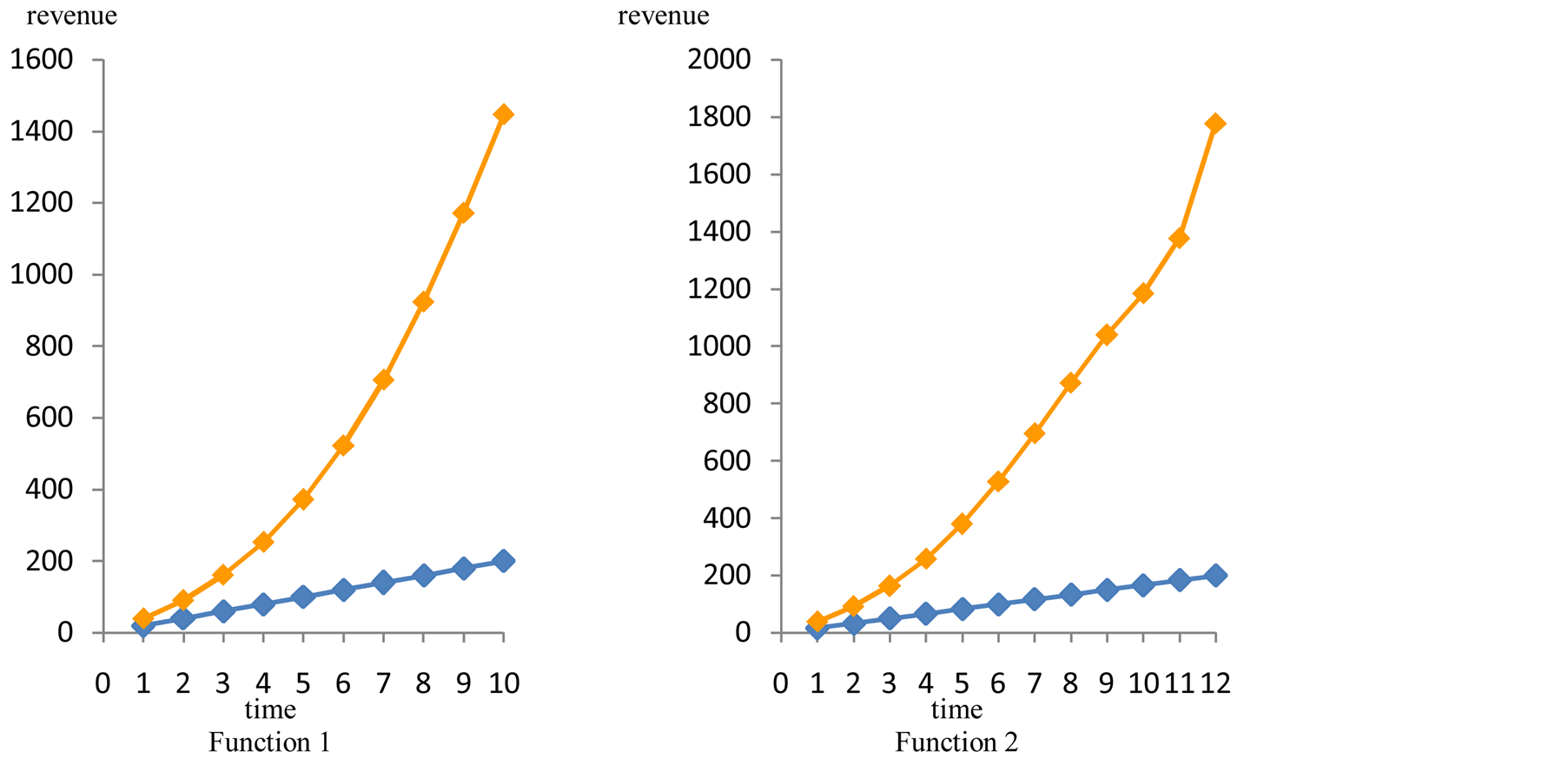
Figure 6. Revenues vs time. Multiple case: two functions on sale. Interest −1. Sensitivity 1.
6. Conclusions
When there is complete information on demand, according to Gallego and van Ryzin [2] , the fixed-pricing strategy leads to near optimal results.
When there is uncertainty about demand, pricing policies obtained by the models that make assumptions about demand may fail in actual applications.
In this paper, we study the dynamic problem of multi-product revenue management, without assuming apriori knowledge about demand. We develop and implement an algorithm of dynamic pricing allocation, capable of learning from the past using a heuristic strategy enabling benefits to grow from the sale of a limited inventory with different classes of products in a finite-time horizon.
So as to make computational simulations more realistic, we have also developed an algorithm that can dynamically determine the demand for each time period, depending on the prices being offered as well as on the time and remaining inventory.
Finally, we develop a tool based on a Java application allowing you to perform a virtual sale process, testing different pricing strategies and analyzing the results obtained.
The results of the computational simulations carried out with the proposed strategy have shown a significant performance gain with respect to the fixed-price strategy.
In the future, we intend to continue calibrating some of the parameters of the dynamic simulation model of the demand and pricing, using actual data on demand and on the sales process. Another line of future research is the use of agent based models allowing us to build a virtual sale considering different types of buyers and sellers interacting according to their beliefs and who make decisions about buying and selling, respectively, based on a series of factors characterizing the process.
References
- Talluri, K.T. and van Ryzin, G.J. (2004) The Theory and Practice of Revenue Management. Springer Science + Business Media, Berlin.
- Gallego, G. and van Ryzin, G. (1994) Optimal Dynamic Pricing of Inventories with Stochastic Demand over Finite Horizons. Management Science, 40, 999-1020. http://dx.doi.org10.1287/mnsc.40.8.999
- Bertsimas, D. and Perakis, G. (2006) Dynamic Pricing: A Learning Approach. Mathematical and Computational Models for Congestion Charging. Applied Optimization, 101, 45-79. http://dx.doi.org/10.1007/0-387-29645-X_3
- Cope, E. (2006) Bayesian Strategies for Dynamic Pricing in E-Commerce. Naval Research Logistics, 54, 265-281. http://dx.doi.org/10.1002/nav.20204
- Lobo, M.S. and Boyd, S. (2003) Pricing and Learning with Uncertain Demand. http://www.stanford.edu/~boyd/papers/pdf/pric_learn_unc_dem.pdf
- Gallego, G. and van Ryzin, G. (1997) A Multiproduct Dynamic Pricing Problem and its Applications to Network Yield Management. Operations Research, 45, 24-41.
- Besbes, O. and Zeevi, A. (2006) Blind Nonparametric Revenue Management: Asymptotic Optimality of a Joint Learning and Pricing Method. Working Paper, Stanford Graduate School of Business.
- Aviv, Y. and Pazgal, A. (2005) A Partially Observed Markov Decision Process for Dynamic Pricing. Management Science, 51, 1400-1416. http://dx.doi.org/10.1287/mnsc.1050.0393
- Araman, V.F. and Caldentey, R. (2009) Dynamic Pricing for Nonperishable Products with Demand Learning. Operations Research, 57, 1169-1188.http://dx.doi.org/10.1287/opre.1090.0725
- Lin, K.Y. (2006) Dynamic Pricing with Real-Time Demand Learning. European Journal of Operations Research, 174, 522-538. http://dx.doi.org/10.1016/j.ejor.2005.01.041
- Narahari, Y., Raju, C.V.L., Ravikumar, K. and Shah, S. (2005) Dynamic Pricing Models for Electronic Business. Sadhana, 30, 231-256. http://dx.doi.org/10.1007/BF02706246
- Farias, V.F. and Van Roy, B. (2010) Dynamic Pricing with a Prior on Market Response. Operations Research, 58, 16- 29. http://dx.doi.org/10.1287/opre.1090.0729
- DiMicco, J.M., Greenwald, A. and Maes, P. (2003) Learning Curve: A Simulation-Based Approach to Dynamic Pricing. Electronic Commerce Research, 3, 245-276.

