American Journal of Operations Research
Vol.4 No.1(2014), Article ID:42348,12 pages DOI:10.4236/ajor.2014.41004
Monotonic Vector Space Model (І): Concepts and Operations
Jianwen Hu
National University of Defense Technology, Changsha, China
Email: hjwc3i@sina.com
Copyright © 2014 Jianwen Hu. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Jianwen Hu. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received October 29, 2013; revised November 29, 2013; accepted December 7, 2013
ABSTRACT
Monotonic vector space (MVS), as a novel model in which there exist some monotonic mappings, is proposed. MVS model is an abstract of many practical problems (such as image processing, system capability engineering, etc.) and includes many useful important operations. This paper, as the first one of series papers, discusses the MVS framework, relative important concepts and important operations including partition, synthesis, screening, sampling, etc. And algorithms for these operations are the focus of this paper. The application of these operations in system capability engineering will be dealt with in the second part of this series of papers.
Keywords: Monotonic Vector Space; Operations; Partition; Synthesis; Screening; Sampling
1. Introduction
MVS is a special vector space where there exist some monotonic mappings. This model actually represents a lot of practical problems. Several examples are given as follows:
Example 1 (Figure 1). Electric field intensity of point charge can be discussed in a vector space 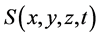 which includes one time dimension and three space dimensions
which includes one time dimension and three space dimensions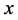 ,
, 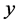 , and
, and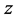 , respectively on
, respectively on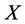 ,
, 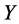 , and
, and 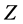 axis of three dimensional coordinate system (see Figure 1). Electric charge quantity of the point charge is also assumed to decrease with time increasing. So, it can be easily understood that there exists monotonic function relation between the electric field intensity
axis of three dimensional coordinate system (see Figure 1). Electric charge quantity of the point charge is also assumed to decrease with time increasing. So, it can be easily understood that there exists monotonic function relation between the electric field intensity 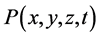 of point charge and the arbitrary one of the above four indices. This means
of point charge and the arbitrary one of the above four indices. This means 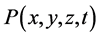 will monotonically increase or decrease with one of four indices changing monotonically while the others maintaining to be constants. Just in this sense,
will monotonically increase or decrease with one of four indices changing monotonically while the others maintaining to be constants. Just in this sense, 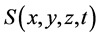 is called monotonic vector space.
is called monotonic vector space.
Example 2 (Figure 2) gives typical electric field intensity lobe of radar antenna. And the electric field intensity of arbitrary point 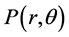 in the main lobe can be calculated in a vector space
in the main lobe can be calculated in a vector space 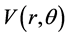 which includes polar radius
which includes polar radius ![]() and polar angle
and polar angle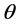 . Obviously,
. Obviously, 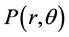 monotonically increases or decreases with each of two parameters changing monotonically while the other maintaining to be constant. So,
monotonically increases or decreases with each of two parameters changing monotonically while the other maintaining to be constant. So, 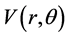 can also be regarded as a MVS.
can also be regarded as a MVS.
Example 3. A monotonic vector space P for a ground-to-air missile system may include the searching radar detecting capability metric dimension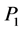 , delay time metric dimension
, delay time metric dimension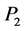 , and tracking radar detecting capability metric dimension
, and tracking radar detecting capability metric dimension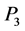 . So, the equation
. So, the equation 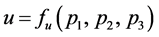 describes the relation between the three system capability metrics (i.e.
describes the relation between the three system capability metrics (i.e. ,
, 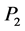 , and
, and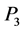 ) and one requirement metric (i.e. the kill probability index u). Function
) and one requirement metric (i.e. the kill probability index u). Function 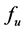 is obviously monotonic, that is to say, the value of u (the kill probability) will monotonically increase or decrease with one of three system capability metric changing monotonically while the others maintaining to be constants. We call
is obviously monotonic, that is to say, the value of u (the kill probability) will monotonically increase or decrease with one of three system capability metric changing monotonically while the others maintaining to be constants. We call 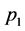 and
and ![]() monotonic increasing metric and
monotonic increasing metric and ![]() monotonic decreasing metric.
monotonic decreasing metric.
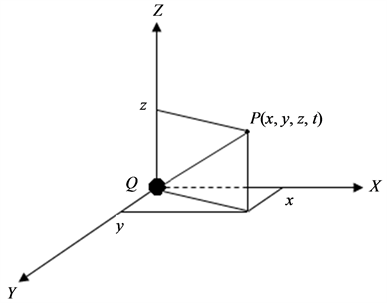
Figure 1. Electric field intensity of point charge.
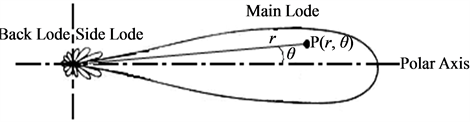
Figure 2. Typical electric field intensity lobe of radar antenna.
Many practical problems can be solved with the operations defined in MVS. For example, for a vector space composed of system capability metrics [1,2], the requirement analysis of capability can be done with partitioning operation in MVS [2]. The screening operation in MVS may be applied for sensibility analysis of system capability metrics. Because Latin Hypercubic sampling [3] operation in MVS reduces variance largely, it is of great value to simulate experiments in system capability engineering.
2. Monotonic Vector Space
Definition 1. Monotonic Vector Space (MVS)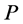 . Let
. Let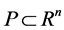 ,
, 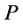 is a point set, i.e., a
is a point set, i.e., a 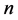 -dimensional subspace of
-dimensional subspace of 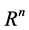 (
(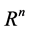 is
is 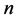 -dimensional Euclid space). There exist mappings such as
-dimensional Euclid space). There exist mappings such as 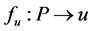 (
( is a real variable and increases or decreases monotonically with each dimension of
is a real variable and increases or decreases monotonically with each dimension of ). Every dimension of
). Every dimension of  can be continuous or discrete type. In most cases, it is very difficult to get the explicit analytic expression of
can be continuous or discrete type. In most cases, it is very difficult to get the explicit analytic expression of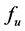 , which usually represents the corresponding relation between input and output of a black box. But many non-analytic methods (such as simulation method, numerical differentiation equation method, etc.) can be used to get the value of
, which usually represents the corresponding relation between input and output of a black box. But many non-analytic methods (such as simulation method, numerical differentiation equation method, etc.) can be used to get the value of 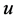 (output).
(output). 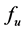 can be classified into deterministic type and stochastic type. If
can be classified into deterministic type and stochastic type. If 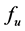 is of stochastic type, then
is of stochastic type, then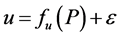 ,
,  is a random variable and
is a random variable and .
.
According to the different type combination of dimension and mapping, MVS can be classified into four types, i.e. discrete deterministic type, continuous deterministic type, discrete stochastic type, and continuous stochastic type. The MVS researching framework is shown in Figure 3. Since many practical problems can be solved with the operations defined in MVS, mentioned as above, the discussion about operations related to MVS will be the focus of this paper. These operations usually include partitioning, synthesizing, screening, sampling, searching, and so on.
• Partitioning. This operation is used to attain the effective area, which covers all the points satisfying certain requirement, through segmenting MVS according to certain requirement criteria. For example, the effective detecting range of a jammed radar, the effective capability indicators fields, and so on, can be gotten through carrying out partitioning operation in MVS.
• Synthesizing. This operation is used to get the synthesized area of several effective areas, each of which contains points meeting different requirement targets. For example, acquiring the intersection of several effective areas in MVS is a typical synthesizing operation.
• Screening. This operation is used to find the essential elements such as key dimensions, key subarea, etc, in the MVS. With this operation, some less important dimensions or subarea of MVS can be overlooked in the tackling process of the practical problems. And thus the computation burden of other operations in MVS can be decreased remarkably.
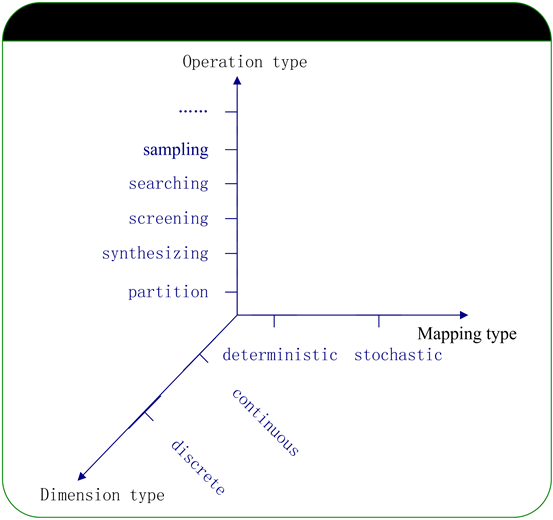
Figure 3. MVS researching frame.
• Sampling. If the mapping in MVS is of stochastic type, sampling the vector points in a large-scale MVS with high efficiency and quality have significance on stochastic simulation experiment (might be considered as stochastic mapping) in MVS.
• Searching. This operation is to find high sensitivity region for some mappings in MVS.
• Other operations. There are some other operations except for the above mentioned, such as slicing, projecting, rotating, etc. These operations, similar to OLAP or data mining, are useful for getting interesting information in the high dimensional MVS.
To solve practical problems, some new operations (except for those mentioned above) in MVS may need to be studied. In the following sections of this paper, the algorithms for partitioning operation in continuous/discrete-type MVS, synthesizing operation in continuous-deterministic-type MVS, sampling operation in stochastic-type MVS, screening operation and Searching operation in corresponding MVS, and so on, will be dealt with in detail as the following sections.
3. The Algorithm for Partition Operation in Mvs of Continuous Deterministic Type
Partitioning is a very valuable operation in MVS and can be used to solve many practical problems such as capability requirement analysis, imaging processing, multi-objective optimization, etc. The requirement-based partitioning operation in MVS of continuous deterministic type is to be discussed in this section.
In the mapping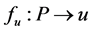 ,
, 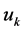 is a specified requirement value and
is a specified requirement value and 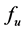 is of deterministic type. With the requirement-based partitioning operation, MVS will be divided into two parts, i.e., the requirement-meeting part (zone) and the requirement-not-meeting part (zone). The requirement-meeting zone is called monotonic vector requirement locus (MVRL) in this paper. MVRL is critical for system capability analysis and design.
is of deterministic type. With the requirement-based partitioning operation, MVS will be divided into two parts, i.e., the requirement-meeting part (zone) and the requirement-not-meeting part (zone). The requirement-meeting zone is called monotonic vector requirement locus (MVRL) in this paper. MVRL is critical for system capability analysis and design.
For simplicity, all the dimensions of MVS are assumed to be monotonically increasing (monotonically decreasing dimension can also be easily transformed into monotonically increasing dimension). MVRL is the set of points meeting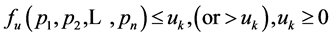 . And the value field of each dimension
. And the value field of each dimension 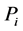 is transformed into interval [0,Vi].
is transformed into interval [0,Vi].
3.1. Some Definitions and Theorems
According to 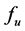 and requirement constraints, MVRL can be produced through finding out all the requirementmeeting points of MVS. Since it is usually very difficult to get the analytic function of
and requirement constraints, MVRL can be produced through finding out all the requirementmeeting points of MVS. Since it is usually very difficult to get the analytic function of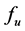 , MVRL-acquiring method based on
, MVRL-acquiring method based on 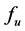 without analytic expression, therefore, will be the discussion emphasis in this paper.
without analytic expression, therefore, will be the discussion emphasis in this paper.
Definition 2. The minimal envelop hyperbox (MEH). MEH refers to the cross product of each dimension’s interval [lower bound, upper bound] and it may also be represented as such simplified form
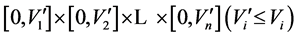 .
.
For example, assuming that x, y are the indexes of a system and that the MVRL is the point set meeting the inequation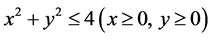 , the field
, the field 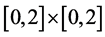 can be regarded as the minimal envelop hyperbox. Any point in the MEH is not bound to be in the MVRL, but any point outside the MEH is bound to be outside the MVRL.
can be regarded as the minimal envelop hyperbox. Any point in the MEH is not bound to be in the MVRL, but any point outside the MEH is bound to be outside the MVRL.
Definition 3. The maximal included hyperbox (MIH) and its opposite hyperbox. The MIH is wholly contained in the MVRL and its diagonal is in the superposition state with the diagonal of the MEH. We can attain the MIH through dividing the interval of the MEH’s each dimension with the same proportion. We give the rigid mathematics definition of the MIH as follow. Set a coefficient 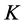
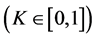 and let
and let
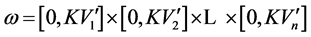
and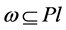 .
.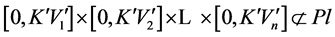
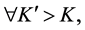 . Furthermore, we define
. Furthermore, we define 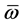 as the opposite hybperbox of
as the opposite hybperbox of 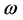 and the expression of
and the expression of 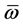 is described as
is described as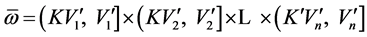 .
.
For the example mentioned above, 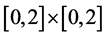 is the minimal envelop hyperbox (MEH).
is the minimal envelop hyperbox (MEH). 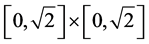
is the maximal included hyperbox (MIH) and 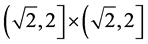 is the opposite hyperbox with
is the opposite hyperbox with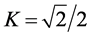 .
.
Theorem 1. Any point in the opposite hyperbox of the maximal included hyperbox does not meet the system requirement, i.e., is not in the MVRL.
Let 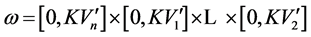
Assume 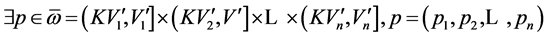 and
and 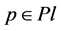
Let
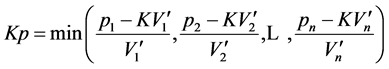
(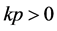 according to Definition 3)
according to Definition 3)
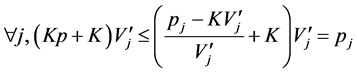
Let
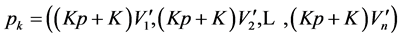
and
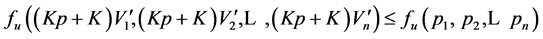
(according to the monotonic property of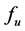 ).
).
In addition, 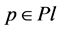 , so
, so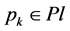 . With the monotonic property of
. With the monotonic property of  and
and
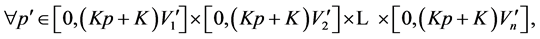
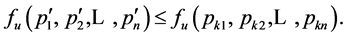
So
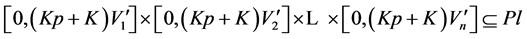 which contradicts the assumption that
which contradicts the assumption that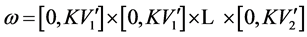 , is the maximal included hyperbox since
, is the maximal included hyperbox since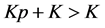 .
.
3.2. The Algorithm
This algorithm recursively approximates MVRL with MIHs, and the algorithm steps are as follows.
Step 1 Determine the requirement 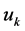 for Pl (MVRL),
for Pl (MVRL), 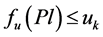
Step 2 Find the minimal envelop hyperbox (MEH):
Step 2.1 Set![]() ;
;
Step 2.2 All dimensions except the kth dimension are set to 0 (the minimal value). Due to the monotonic property of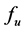 , binary method is applied to get the upper bound of the kth dimension;
, binary method is applied to get the upper bound of the kth dimension;
Step 2.3 If![]() , the cross product of interval [0, upper bound ] of each dimension is the minimal envelop hyperbox (MEH), go to Step 3, else, set
, the cross product of interval [0, upper bound ] of each dimension is the minimal envelop hyperbox (MEH), go to Step 3, else, set ![]() and go to Step 2.2.
and go to Step 2.2.
Step 3 Find the MIH:
Step 3.1 Judge whether the volume of MEH is smaller than the value E (which represents the exit condition). If true, make interpolation and exit. If the interval length of one certain dimension in the MEH is smaller than a certain value, this dimension need not be divided anymore and thus will be deleted;
Step 3.2 According to the monotonic property of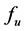 , it is obvious that when
, it is obvious that when
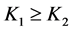 ,
,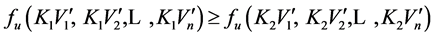 .
.
So, the binary method is applied to get the 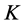 (the dividing ratio for MIH) and the MIH;
(the dividing ratio for MIH) and the MIH;
Step 3.3 Each dimension interval of the MEH is divided into two parts. One part is inside the MIH and marked by “0”, and the other is outside the MIH and marked by “1”. So, there are altogether 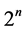 (n is the number of dimensions) interval combinations, each of which is denoted by a binary code containing n digits. The numerical value of the binary code is from 0 to 2n−1. Code “0” whose binary digits are all 0 represents the MIH where any point meets the system requirement and will be saved. Code “1” whose binary digits are all 1 represents the opposite hyperbox of the MIH where any point does not meet the system requirement according to Theorem 1 and will be removed. Regard each of the rest combinations as a new MEH and recursively go to Step 3.
(n is the number of dimensions) interval combinations, each of which is denoted by a binary code containing n digits. The numerical value of the binary code is from 0 to 2n−1. Code “0” whose binary digits are all 0 represents the MIH where any point meets the system requirement and will be saved. Code “1” whose binary digits are all 1 represents the opposite hyperbox of the MIH where any point does not meet the system requirement according to Theorem 1 and will be removed. Regard each of the rest combinations as a new MEH and recursively go to Step 3.
Figure 4 illustrates the algorithm process of acquiring the MVRL. Assume that the MVRL is the point set
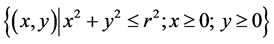 and the rectangle marked by code “00” is the so-called MIH. Firstly, using the binary searching method along the diagonal of MEH, we can find the proper point in it and this point will finally locate the MIH. Secondly, get rid of the opposite hyperbox (marked by code “11”) and regard each of the other hyperboxes as a MEH. Finally, acquire all the MIHs of which the MVRL is composed through repeating the process recursively.
and the rectangle marked by code “00” is the so-called MIH. Firstly, using the binary searching method along the diagonal of MEH, we can find the proper point in it and this point will finally locate the MIH. Secondly, get rid of the opposite hyperbox (marked by code “11”) and regard each of the other hyperboxes as a MEH. Finally, acquire all the MIHs of which the MVRL is composed through repeating the process recursively.
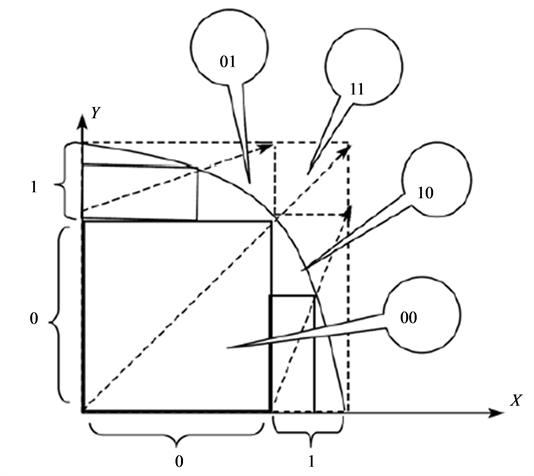
Figure 4. The process of acquiring the MVRL.
There exist monotonic realtions in MVS, thus we can get the special benefit of high efficiency as many famous algorithms which reduce calculation based on monotonicity (i.e. apriori algorithm in data mining [10], binary searching algorithm, branch and bound algorithm etc.)
This algorithm can be applied to solve many problems in which there exists the monotonicity. For example,it can be applied to efficiently draw the radar detecting range when the radar is jammed by jammer and efficiently seek the pareto locus in multi-object programming.
This algorithm is essentially a partition technique for some special figures. If the assumptions is met, it is superior to the classic triangulation method [11,12] by triangular or tetrahedron for the following reasons:
1) As the above mentioned, hyperbox is more suitable for many kinds of operations than triangular or tetrahedron.
2) It is effective and efficient to partition 3-dimensional or more than 3-dimensioal figure for which triangulation method is very difficult to be applied [12].
4. The Algorithm for Partitioning Operation in MVS of Discrete Deterministic Type
An effective algorithm for partitioning in MVS of discrete type is proposed in this section. Based on the assumption that each dimension of MVS is divided into several segments, this algorithm can efficiently find out the combinations which meet the specified requirements. If each dimension of m-dimension MVS is divided into 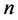 segments, each of which is actually represented by the upper limit value of its own, there will be
segments, each of which is actually represented by the upper limit value of its own, there will be 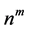 combinations. According to the rule that segment with larger dimension value is tagged by lager mark, all the segments of each dimension are labeled with marks #1, #2, #3,···, and #n. The details of related algorithm are stated as follows.
combinations. According to the rule that segment with larger dimension value is tagged by lager mark, all the segments of each dimension are labeled with marks #1, #2, #3,···, and #n. The details of related algorithm are stated as follows.
Step 1 Specify a representative value (RV) for each combination and fill all the RVs into the combination table. RVs will be used to determine which combination is the next one to be judged whether meeting the requirement or not. Definition of RV is based on two other basic conceptions, i.e., the lower-cut set and the uppercut set. Explanations for these conceptions will be given with the following example. For example, if the combination #3#3#3#4 with m = 4 and n = 5 meet the specified requirement (i.e., 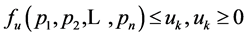 and
and 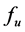 being monotonically increasing), there will be other 108 combinations
being monotonically increasing), there will be other 108 combinations 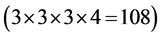 which can also meet the requirement. Every digit of each of
which can also meet the requirement. Every digit of each of 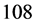 combinations (e.g., #1#1#1#1, #1#2#2#2, and #3#3#3#3.) is less than or equal to the corresponding digit of the combination #3#3#3#4, and all these
combinations (e.g., #1#1#1#1, #1#2#2#2, and #3#3#3#3.) is less than or equal to the corresponding digit of the combination #3#3#3#4, and all these 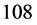 combinations constitute the so-called lower-cut set of combination #3#3#3#4. Similarly, if the above combination doesn’t meet the requirement, there will be other 54 combinations
combinations constitute the so-called lower-cut set of combination #3#3#3#4. Similarly, if the above combination doesn’t meet the requirement, there will be other 54 combinations 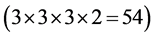 which can not meet the requirement either. And all these
which can not meet the requirement either. And all these ![]() combinations (e.g., #4#4#4#4, #4#4#3#5, and #5#5#5#5.) constitute the socalled upper-cut set of combination #3#3#3#4. To determine an appropriate representative value for a certain combination, it may be helpful to take its lower-cut set and upper-cut set into account. So the calculation formula for RV can be stated as follows.
combinations (e.g., #4#4#4#4, #4#4#3#5, and #5#5#5#5.) constitute the socalled upper-cut set of combination #3#3#3#4. To determine an appropriate representative value for a certain combination, it may be helpful to take its lower-cut set and upper-cut set into account. So the calculation formula for RV can be stated as follows.
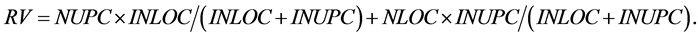
In the above formula, 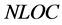 ,
, 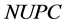 ,
, 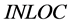 , and
, and 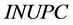 respectively denotes the present total element number of lower-cut set, the present total element number of upper-cut set, the initial total element number of lower-cut set, and the initial total element number of upper-cut set. For example, at the very beginning, the RV of combination #3#3#3#4 is
respectively denotes the present total element number of lower-cut set, the present total element number of upper-cut set, the initial total element number of lower-cut set, and the initial total element number of upper-cut set. For example, at the very beginning, the RV of combination #3#3#3#4 is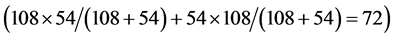 . When a certain combination meet the requirement, all the elements in its lower-cut set are cut. Otherwise, all the elements in its upper-cut set are cut. In this sense, RV reveals the calculation burden that may be alleviated by the corresponding combination.
. When a certain combination meet the requirement, all the elements in its lower-cut set are cut. Otherwise, all the elements in its upper-cut set are cut. In this sense, RV reveals the calculation burden that may be alleviated by the corresponding combination.
Step 2 Scan the combination table, which is dimensioned by a heap structure to make the combination with the maximal RV found quickly, and select the combination with the maximal RV by using the greedy tactics. Firstly, assume combination #I1#I2#I3#I4 is the one with the maximal RV at present.
1) If the combination #I1#I2#I3#I4 meets the specified requirement, all the elements in its lower-cut set will be deleted from the combination table, which likely makes the lower-cut set element number of any other combination decreased. The method for adjusting the lower-cut set element number of any other combination (such as #J1#J2#J3#J4) is not so complicated. With setting #Ki =min(#Ii, #Ji)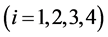 , the adjusted lower-cut set element number of combination #J1#J2#J3#J4 equals to subtracting the lower-cut set element number of combination #K1#K2#K3#K4 from the original lower-cut set element number of combination #J1#J2#J3#J4. If #K1#K2#K3#K4 is not in the combination table, the original lower-cut set element number of combination #J1#J2#J3#J4 will remain unchanged.
, the adjusted lower-cut set element number of combination #J1#J2#J3#J4 equals to subtracting the lower-cut set element number of combination #K1#K2#K3#K4 from the original lower-cut set element number of combination #J1#J2#J3#J4. If #K1#K2#K3#K4 is not in the combination table, the original lower-cut set element number of combination #J1#J2#J3#J4 will remain unchanged.
2) If the combination #I1#I2#I3#I4 does not meet the specified requirement, all the elements in its upper-cut set will be deleted from the combination table, which likely makes the upper-cut set element number of any other combination decreased. The method for adjusting the upper-cut set element number of any other combination (such as #J1#J2#J3#J4) is not so complicated. After setting #Ki = min(#Ii, #Ji)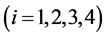 , the adjusted upper-cut set element number of combination #J1#J2#J3#J4 equals to subtracting the upper-cut set element number of combination #K1#K2#K3#K4 from the original upper-cut set element number of combination #J1#J2#J3#J4. If #K1#K2#K3#K4 is not in the combination table, the original upper-cut set element number of combination #J1#J2#J3#J4 will remain unchanged.
, the adjusted upper-cut set element number of combination #J1#J2#J3#J4 equals to subtracting the upper-cut set element number of combination #K1#K2#K3#K4 from the original upper-cut set element number of combination #J1#J2#J3#J4. If #K1#K2#K3#K4 is not in the combination table, the original upper-cut set element number of combination #J1#J2#J3#J4 will remain unchanged.
Step 3 Adjust the combination table. If the selected combination meets the specified requirement, this combination and all the elements in its lower-cut set will be deleted from the combination table, or else this combination and all the elements in its upper-cut set will be deleted from the combination table. For example, if combination #3#3#3#4 meets the specified requirement, all the elements in its lower-cut set such as #1#1#1#1, #1#2#2#2, #3#3#3#3, etc. in the combination table would be deleted.
Step 4 Go to step 2 until the combination table is empty.
To illustrate the above algorithm in detail, it is necessary to discuss an example. In the following example, a discrete MVS with four dimensions (i.e., 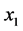 ,
, 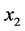 ,
, 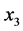 and
and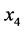 ) is assumed and each dimension is divided into four segments whose upper limit values are respectively 2(#1, No.1), 3(#2, No.2), 4(#3, No.3), and 5(#4, No.4). And the requirement condition is specified as
) is assumed and each dimension is divided into four segments whose upper limit values are respectively 2(#1, No.1), 3(#2, No.2), 4(#3, No.3), and 5(#4, No.4). And the requirement condition is specified as .
.
Now the partitioning operation can be carried out under the guidance of the above algorithm.
Step 1 Determine the corresponding RVs for all the combinations, the number of which is 256 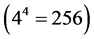 due to
due to  and
and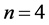 , and fill all the RVs into the combination table (shown in Figure 5).
, and fill all the RVs into the combination table (shown in Figure 5).
Step 2 Single out the combination with the maximal RV from combination table. At the very beginning, combination #3#3#2#2 is found to be the combination with the maximal RV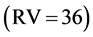 .
.
Step 3 Adjust the combination table. For example, since combination #3#3#2#2 meets the specified requirement, on the one hand, this combination and all the elements in its lower-cut set are to be deleted from the combination table; on the other hand, the lower-cut set element number of any remaining combination in the combination table may also need to be modified. Now take the combination #4#1#1#1 as an example. Combination
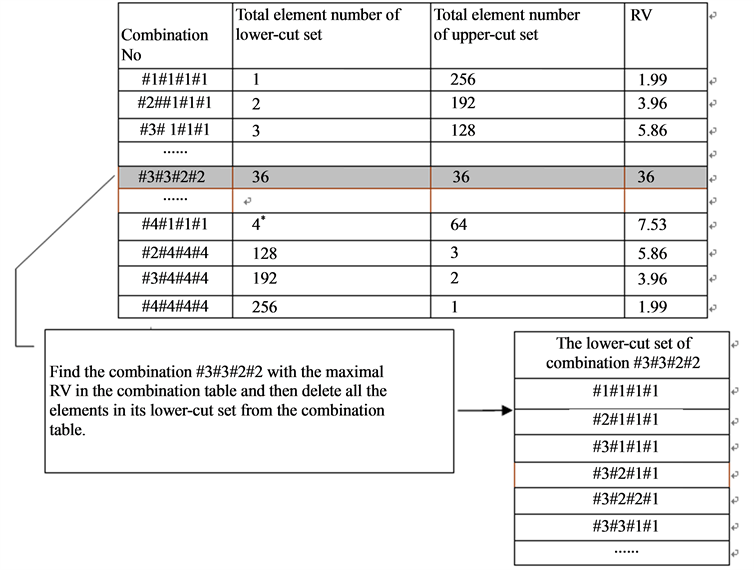
Figure 5. Combination table.
#K1#K2#K3#K4 = #3#1#1#1 with #I1#I2#I3#I4 = #3#3#2#2 and #J1#J2#J3#J4 = #4#1#1#1 can be easily gotten by using the method mentioned above. Because combination #3#1#1#1 is found to be still in the combination table, the lower-cut set element number and RV of combination #4#1#1#1 must be modified. So the adjusted lower-cut set element number of #4#1#1#1 is equal to its original lower-cut set element number minus the lower-cut set element number of combination #3#1#1#1 (i.e.,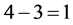 ). Based on the adjusted lower-cut set element number of #4#1#1#1, its adjusted RV can also be acquired. The adjusted lower-cut set element numbers and adjusted RVs of other combinations are shown in Table1
). Based on the adjusted lower-cut set element number of #4#1#1#1, its adjusted RV can also be acquired. The adjusted lower-cut set element numbers and adjusted RVs of other combinations are shown in Table1
Step 4 Go to step 2 until the combination table is empty. In this example, all the combinations meeting the specified requirement such as #1#2#2#4, #2#1#2#4,···, #3#3#2#2, etc., are acquired after 67 iterations, which means that only about one quarter of all the combinations are calculated and the algorithm elaborated in this section is of high efficiency.
5. The Algorithm for Synthesizing Operation in MVs of Continuous Type
For a practical problem, there are usually several different kinds of requirement targets, each of which obviously corresponds to a different MVRL. Therefore, intersection operation of multiple MVRLs is of great significance to the solution of one practical problem. In this section, two algorithms for one kind of synthesizing operations (i.e., intersection operation of multiple MVRLs) are presented.
5.1. Algorithm Based on Direct Method
The shape of a MVRL approached by many hyperboxes is usually irregular. The intersection of multiple MVRLs is approximately to be the intersection of the hyperboxes included in the MVRLs. Therefore, the former can be acquired through finding out the latter. The method of seeking the total intersection of all the hyperboxes is very simple. However, its time cost is large. For example, if there are two MVRLs whose numbers of hyperboxes are respectively 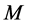 and
and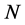 ,
, 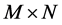 intersection operations have to be performed to get the total intersection of all the hyperboxes. And the time complexity is
intersection operations have to be performed to get the total intersection of all the hyperboxes. And the time complexity is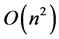 , where
, where 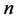 is the hyperbox number of one MVRL.
is the hyperbox number of one MVRL.
Actually, all the MEHs and MIHs acquired in the process of producing a MVRL can be naturally organized into an including relation tree (heap) shown in Figure 6.
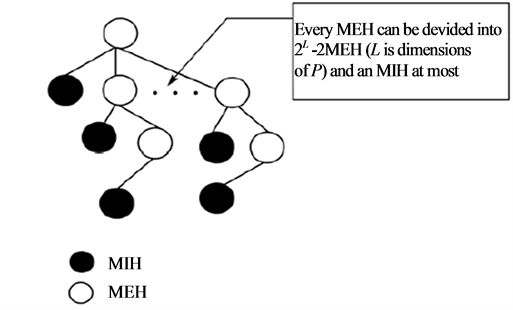
Figure 6. The tree consisting of MEH and MIH.
5.2. Algorithm Based on Approaching Method
If all the requirements have the same constraint direction on any system dimension, i.e., achievement degree of all the requirement indices becoming larger or smaller with any system dimension value increasing or decreasing, approaching method can be used to seek the intersection of multiple MVRLs. The algorithm based on approaching method is stated as follows.
Step 1 Get the intersection of the MEHs of all the MVRLs, i.e., the MEH of the intersection of all the MVLRs.
Step 2 Seek all the MIHs, which approximately compose the intersection of all MVRLs, with the related algorithm mentioned above.
The above two steps are illustrated in Figure 7.
If this tree is saved in the memory, the time cost of the direct method may be largely reduced. The reason is that if the hyperbox of one MVRL has null intersection with one certain MEH of another MVRL, it will have no common intersection with all the MIHs included in this MEH, and so, the related intersection operations can be omitted.
Besides intersection operation, which is a relatively simple and typical synthesizing operation, there are still some other complicated synthesizing operations such as union operation, union-intersection mixed operation (i.e., carrying out intersection operation on some dimensions and union operation on the others). And all of these synthesizing operations are very useful in solving practical problems and should be studied thoroughly in the future.
6. The Algorithm for Screening Operation in MVS of Stochastic Type
Dimensions screening is very important for all kinds of operations in MVS because it can alleviate calculation burden to a great extent. Pareto principle or 20 - 80 rule implies that only a few factors are really important. The purpose of screening is to find out the really important ones among all the dimensions of MVS. As mentioned above, in the stochastic type MVS, the mapping 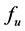 will be of statistical type, i.e.,
will be of statistical type, i.e., 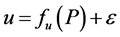 where
where 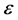 is a random value and
is a random value and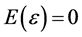 .
.
Sequential bifurcation (SB) method originally developed by Bettonvil in his doctoral dissertation [4] is a very efficient and effective one among all the screening methods and will be introduced in detail in this section. And the summarization of Bettonvil’s doctoral dissertation is presented by reference [5]. Assuming a specific metamodel, an approximation of the monotonic mapping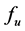 , is necessary for a screening. Characteristics of the assumed metamodel for SB in this part include two points.
, is necessary for a screening. Characteristics of the assumed metamodel for SB in this part include two points.
1) The metamodel of 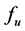 is of monotonic type, which is obviously met in MVS.
is of monotonic type, which is obviously met in MVS.
2) The metamodel is a first-order polynomial with 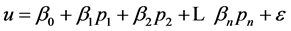 and
and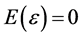 .
.
The dimensions 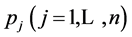 of MVS are standardized such that they are either –1 or +1 which represent the maximal or minimal value for
of MVS are standardized such that they are either –1 or +1 which represent the maximal or minimal value for![]() . This scaling implies that the dimensions may be ranked (sorted) by their main effects; i.e., the most important dimension is the one with the largest absolute value of its first-order effect or main effect; the least important dimension is the one with the effect closest to zero.
. This scaling implies that the dimensions may be ranked (sorted) by their main effects; i.e., the most important dimension is the one with the largest absolute value of its first-order effect or main effect; the least important dimension is the one with the effect closest to zero.
To explain some mathematical details of SB, the following notations are used.
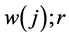 : observed output with the dimension 1 through j set to their high levels and the remaining factors set to their low levels, in replication r;
: observed output with the dimension 1 through j set to their high levels and the remaining factors set to their low levels, in replication r;
 (a) (b)
(a) (b)
Figure 7. The approaching method to acquire the intersection of MVRL1 and MVRL2.
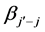 : sum of main effects of dimension
: sum of main effects of dimension 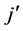 through
through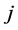 ; so
; so 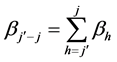
A simple estimate of this group effect based on replication r is 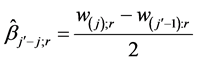
SB starts with calculating the two most extreme scenarios: in scenario 1, all k dimensions are set at their low levels so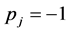 ; in scenario 2, all these factors are high so
; in scenario 2, all these factors are high so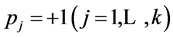 . If the above metamodel is valid, then
. If the above metamodel is valid, then
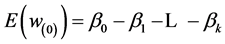 and
and 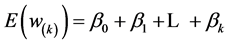
so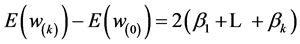 .
.
Likewise it follows that the individual main effect is estimated:
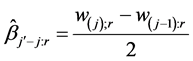
The SB procedure is sequential. Its first step places all dimensions into a single group, and tests whether or not that group of dimensions has an important effect. If the group indeed has an important effect, then the second step splits the group into two subgroups (i.e., bifurcates) and tests each of these subgroups for importance. The next steps continue in a similar way, discarding unimportant subgroups and splitting important subgroups into smaller subgroups. In the Final step, all individual dimensions that are not in subgroups identified as unimportant, are estimated and tested. The steps are showed below:
1) Select the group whose dimensions are from 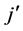 to
to 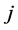 and estimate expected value of the
and estimate expected value of the
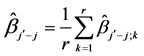 ;
;
2) If this group’s 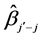 smaller than
smaller than ![]() (a threshold value), then all individual dimensions(from
(a threshold value), then all individual dimensions(from 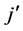 to
to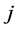 ) that are in this group are identified as unimportant;
) that are in this group are identified as unimportant;
3) If this group’s 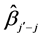 larger than
larger than![]() , then insert this group into the group table ascendingly according to
, then insert this group into the group table ascendingly according to 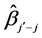 and select the group with the maximal value of
and select the group with the maximal value of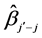 , until all individual dimensions that are not in subgroups identified as unimportant are estimated and tested.
, until all individual dimensions that are not in subgroups identified as unimportant are estimated and tested.
This section introduces a simple algorithm (i.e., sequential bifurcation) for screening operation in MVS. SB method based on some assumptions is effective and efficient in the solving of many practical problems(i.e., supply chain analysis [6), And some investigator, such as the authors of [7-9] have successfully extended the simple SB.
7. The Sampling Operation in MVS of Stochastic Type
Sampling operation is important for experiments in MVS. The purpose of this operation is to effectively and efficiently select the points used in all kinds of experiments. Latin hypercube sampling (LHS) is very fit for MVS. The algorithm for acquiring 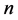 sampling points in the d-dimension hypercube
sampling points in the d-dimension hypercube 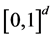 with LHS method is discussed in this section. Coordinate value interval
with LHS method is discussed in this section. Coordinate value interval 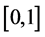 of each dimension is equally divided into
of each dimension is equally divided into 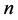 segments and the
segments and the ![]() segment
segment 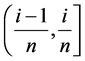 is marked by its segment number
is marked by its segment number 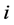
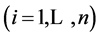 . A random permutation of
. A random permutation of 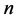 segment numbers of the
segment numbers of the ![]() dimension is denoted as
dimension is denoted as 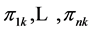
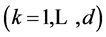 . And
. And ![]() mutual independent random permutations constitute a
mutual independent random permutations constitute a ![]() random matrix
random matrix 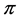
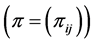 . Such
. Such 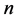 sampling points as
sampling points as 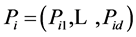
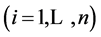 with
with 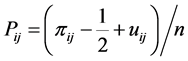
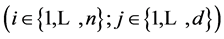 where
where 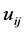 is random variable subject to uniform distribution on
is random variable subject to uniform distribution on 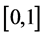 and not only mutual independent but also independent of
and not only mutual independent but also independent of 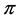 construct a LHS sample. In many aspects, a LHS sample is superior to some other kinds of samples such as the independently and identically distributed (IID) sample gotten with simple random sampling (SRS) method.
construct a LHS sample. In many aspects, a LHS sample is superior to some other kinds of samples such as the independently and identically distributed (IID) sample gotten with simple random sampling (SRS) method.
The relative advantages of LHS method can be revealed with an example. The estimation value
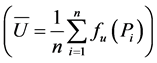 of the mathematical expectation
of the mathematical expectation 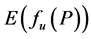 of function
of function 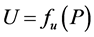 will be different with different sample. And the estimation values based on IID sample, LHS sample, and the sample acquired with stratified sampling (SS) method are respectively denoted as
will be different with different sample. And the estimation values based on IID sample, LHS sample, and the sample acquired with stratified sampling (SS) method are respectively denoted as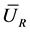 ,
, 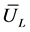 , and
, and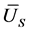 . The reference [3] has proved the unbiasedness of these estimations and also given the variances of
. The reference [3] has proved the unbiasedness of these estimations and also given the variances of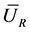 ,
,  , and
, and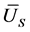 .
.
In the above expressions, 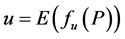 ,
, 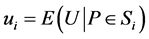 for LHS sample, and
for LHS sample, and 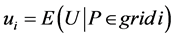 for SS sample (referring to [3] for other details). Since
for SS sample (referring to [3] for other details). Since 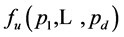 will monotonically increase or decrease with each of
will monotonically increase or decrease with each of ![]() indices changing monotonically while the others maintaining to be constants in MVS, such conclusion as
indices changing monotonically while the others maintaining to be constants in MVS, such conclusion as 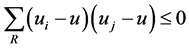 can be gotten. Actually, the above conclusion, with which another conclusion (i.e.,
can be gotten. Actually, the above conclusion, with which another conclusion (i.e.,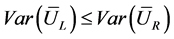 ) can be deduced, has already been proved by reference [3]. Thus it can be seen that LHS is a sampling method fit for experiments in MVS.
) can be deduced, has already been proved by reference [3]. Thus it can be seen that LHS is a sampling method fit for experiments in MVS.
Funding
Supported by NSFC, China, PRC, Grant No 70871120.
[1] REFERENCES
[2] J. W. Hu, et al., “MIS Method (Monotonic Indices Space) and Its Application in Capability Indicators Effectiveness Analysis of a Notional Anti-Stealth Information System,” IEEE Transactions on Systems, Man and Cybernetics PART A, Vol. 39, No. 2, 2009, pp. 407-417.
[3] V. Bouthonnier and A. H. Levis, “System Effectiveness Analysis of C3 Systems,” IEEE Transactions on Systems, Man and Cybernetics, Vol. SMC-14, No.1, 1984, pp. 48-54. http://dx.doi.org/10.1109/TSMC.1984.6313268
[4] M. D. McKay, et al., “A Comparision of Three Methods for Selecting Values of Input Variablea in Analysis of Output from a Computer Codes,” Tehchnometrics, Vol. 21, No. 2, 1979, pp. 239-245.
[5] B. Bettonvil, “Detection of Important Factors by Sequential Bifurcation,” Ph.D. Dissertation, Tilburg University Press, Tilburg, 1996.
[6] B. Bettonvil and J. P. C. Kleijnen, “Searching for Important Factors in Simulation Models with Many Factors: Sequential Bifurcation,” European Journal of Operational Research, Vol. 96, No. 1, 1997, pp. 180-194. http://dx.doi.org/10.1016/S0377-2217(96)00156-7
[7] J. P. C. Kleijnen, B. Bettonvil and F. Persson, “Screening for the Important Factors in Large Discrete-Event Simulation: Sequential Bifurcation and Its Applications,” In: A. Dean and S. Lewis, Eds., Screening: Methods for Experimentation in Industry, Drug Discovery, and Genetics, Springer-Verlag, New York, 2006, pp. 287-307. http://dx.doi.org/10.1007/0-387-28014-6_13
[8] H. Wan, B. E. Ankenman and B. L. Nelson, “Controlled Sequential Bifurcation: A New Factor-Screening Method for DiscreteEvent Simulation,” Operations Research, Vol. 54, No. 4, 2006, pp. 743-755. http://dx.doi.org/10.1287/opre.1060.0311
[9] R. C. H. Cheng, “Searching for Important Factors: Sequential Bifurcation under Uncertainty,” Proceedings of the 1997 Winter Simulation Conference, 1997, pp. 275-280.
[10] B. E. Ankenman, R. C. H. Cheng and S. M. Lewis, “A Polytope Method for Estimating Factor Main Effects Efficiently,” Proceedings of the 2006 Winter Simulation Conference, Monterey, 3-6 December 2006. http://dx.doi.org/10.1109/WSC.2006.323104
[11] R. Agrawal and R. Srikant, “Fast Algorithms for Mining Association Rules,” Proceedings of 1994 International Conference Very Large Data Bases (VLDB’94), Santiago, September 1994.
[12] B. Chazelle and L. Palios, “Triangulating a Non-Convex Polytope,” Discrete & Computational Geometry, Vol. 5, No. 1, 1990, pp. 505-526. http://dx.doi.org/10.1007/BF02187807
[13] J. Ruppert and R. Seidel, “On the Difficulty Triangulating Three-Dimensional Non-Vex Polyhedra,” Discrete & Computational Geometry, Vol. 7, 1992, pp. 227-253.


