Received 27 October 2015; accepted 6 December 2015; published 9 December 2015

ABSTRACT

Acylation of allylic esters with acylsilanes and acylstannanes in the presence of a palladium complex was investigated theoretically using the DFT (B3PW91) method. We examined along the reaction that was reported by Tsuji’s. In this mechanism for generating active species, a Pd dinuclear complex 5 (the reaction of Pd and 2) was produced. Then, 5 is decomposed to two mononuclear complex 6. The reaction of 6 and 1 forms an intermediate 7, which is active species. In catalytic cycle from 7, the O (1) atom of 7 attacks the Si or Sn atom in TS_7-8 to produce 8. Then, the C(1)-C(2) reductive elimination from 8 occurs through the TS_8-9 to yield 9. Therefore, 9 decomposed to Pd(0), 3 and 4. However, reaction mechanism from 9 to 6 should be considered because Pd(0) + 3 + 4 are less stable than 9 by 29.2 kcal/mol, 9 does not decompose. We proposed the reaction mechanism from 9, as shown below: 1) 2 attacks 9 to form 10. 2) 10 released 4 to produce a five coordinated intermediate 11. 3) 11 changes its structure to another π-allyl complex 12. 4) The product 3 was released from 12 and 6 formed again for a next catalytic cycle. The rate-determining step of these reaction is nucleophilic attack of carbonyl oxygen to R^A (7 → 8), and the ∆G^‡ for I, II and III was calculated to be 27.1, 39.1, and 30.9 kcal/mol, respectively. As a result, we elucudated the reaction mechanism of acylation of allylic esters with acylsilanes and acylstannanes in the presence of a palladium complex.

Keywords:

Acylation, Palladium Complex, Theoretical Calculation, Catalytic Cycle

1. Introduction

The palladium-catalyzed acylation of allylic esters has been widely applied in organic synthesis and is one of the most important reactions. Carbanions [1] - [5] , enolates [6] - [10] , and amines [11] - [15] are often employed as the nucleophilic agent of this reaction until now. The acylated products obtained by this reaction are used as materials for constructing natural products, pharmaceutical compounds, low molecular organic compounds, polyesters, and polycarbonates. However, since functional groups that can be directly introduced to the allylic system are still limited, further developments of the research are expected.

In 1993, Tsuji and co-workers found out the palladium-catalyzed silylation reaction of allylic esters with disilanes (Scheme 1) [16] . Additionally, they reported new acylation reaction of allylic ester with acyl silane or acyl stannane based on reactions in the past [17] [18] .

In these reactions, acyl silane and acyl stannane act as the acylating agent in the presence of Pd catalyst. Three kinds of reactions by the difference in the substituents (R^A and R^B) as shown in Scheme 2 were reported by these works. In these three reactions, I and II proceeds, but III does not occur.

Reaction mechanism of this acylation is proposed by Tsuji and co-workers as shown in Scheme 3. The first step of these catalytic cycles is formed a π-aryl complex by Pd complex and 2. After this reaction, a π-aryl complex reacts with 1 to form 4 and a new π-aryl complex. Finally, 3 is generated from a π-aryl complex, a Pd catalyst reproduces. Thus, several experimental works have been well performed, but a reaction mechanism has not been theoretically investigated yet, to our knowledge.

In this study, we theoretically investigated the Pd-catalyzed acylation reaction of allylic ester using the DFT method [19] . Here our attentions were focused on clarifying the reaction mechanism and the substituent effect in these reactions.

Scheme 1. Silylation reaction reported by Tsuji and co-workers.

Scheme 2. Acylation of 2 with 1.

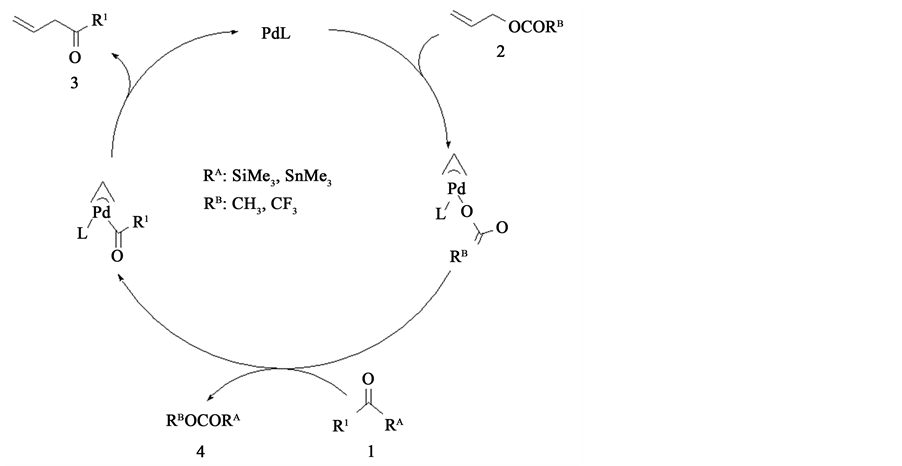
Scheme 3. Catalytic cycle with Pd(II) complex.

2. Computational Details

All geometry optimizations were calculated with the DFT method, where the B3PW91 [20] [21] functional was used for the exchange-correlation term. We ascertained that each equilibrium structure exhibited no imaginary frequencies, and each transition state had only one imaginary frequency. In these calculations, the following basis set system was employed. The (541/541/211/1) [22] [23] basis set was used to represent the valence electrons of Pd, where the effective core potentials (ECPs) were employed to replace core electrons (up to 3d) [24] . The LANL2DZ basis set was used for Sn. For C and O atoms, the usual 6-311G(d) basis sets were employed. For Si atom, the 6-311G(2d) basis set was used. For H atom, the 6-31G(d,p) basis set were employed. To investigate the solvent effects of tetrahydrofuran (THF), we performed single point calculations with the SMD [25] method using the optimized structures. The values of free energies were calculated with thermodynamic cycle [26] .

All of these calculations were carried out with the Gaussian 09 program package [27] .

3. Results and Discussion

The reaction mechanism proposed by Tsuji and co-workers were shown in Scheme 4. In the first step of this reaction mechanism, Pd dinuclear complex 5 is formed to by catalyst and allylic ester. 5 is decomposed into two molecules, Pd mononuclear complex 6 is formed. 1 is close to 6, and intermediate 7 generates.

Although these molecular structures are not known precisely, Pd complex such as 7 were assumed to be the active species in the catalytic cycle for the acylation with allylic ester. However, the reaction mechanism starting from 7 has not yet been investigated. We proposed the reaction mechanism from 7 as shown in Scheme 5. The O(1) atom of 7 attacks the Sn or Si atom through the transition state, TS_7-8, to produce 8. The C(1)-C(2) reductive elimination from 8 occurs through the TS_8-9 to yield 9.

The Sn-C and Sn-O(1) distances of ­7 in Reaction I were calculated to be 2.238 and 2.749Å, respectively (see Figure 1). On the other hand, since the Sn-C and Sn-O(1) distances of 8 in Reaction I were 4.900 and 2.073Å, respectively, the Sn-C bond is broken and new Sn-O(1) bond is formed. In reaction (8 → 9), the Pd-C(1) and Pd-C(2) distances of 8 and 9 in Reaction I were 2.072 and 3.963 Å, respectively. As the reaction progresses, we find out that the Pd-C(2) bond have been dissociated. Moreover, 8 in Reaction I was a π-aryl complex, but 9 in Reaction I was not. Reaction II and III showed these results similar to Reaction I.

The Si-C and the Si-O(1) distances of 7 in Reaction II were 1.939 and 3.030Å, respectively (see Figure 2). On the other hand, the Si-C and Si-O(1) distances of 8 in Reaction II were calculated to be 4.838 and 1.740Å, respectively. When comparing Reaction I and II, the Si-C and Si-O(1) bonds are stronger than the Sn-C and Sn-O(1) bonds. From these results, it was suggested that dissociations of the Sn-C and Sn-O bonds are easier than those the Si-C and Si-O bonds.

Scheme 4. Reaction mechanism proposed by Tsuji and co-workers.

Scheme 5. Proposed reaction mechanism from 7.

The ∆G^‡ values of the reaction (7 → 8) for Reaction I, II and III were calculated to be 27.1, 39.1 and 30.1 kcal/mol, respectively. Additionally, the ∆G^‡ values of the step (8 → 9) for Reaction I, II and III were 21.2, 20.4 and 23.1 kcal/mol, respectively. Intermediates 9 for Reaction I, II and III are much more stable than 7 by 21.2, 21.7 and 34.8 kcal/mol, respectively. As a result, the reactions leading to 9 in Reaction I, II and III will occur easily.

In the proposed reaction mechanism, 9 is dissociated to Pd(0), 3 and 4. Figure 3 displays the free energy change between 9 and three product compounds in Reaction III. Product compounds (Pd(0), 3 and 4) in Reaction III are much more unstable than 9 by 29.2 kcal/mol, it can be considered than this reaction will not proceed. Therefore, we assumed a new reaction shown in Scheme 6.

In this new reaction, 2 attacks 9 to form 10. 4 dissociates from 10, and a five coordinated intermediate 11 is generated. We examined the validity of this reaction mechanism.

The Pd-C(1) and Pd-C(2) bonds of 9 + 2 in Reaction I were dissociated, respectively. Those distances of 10 in Reaction I were 2.123 and 2.162 Å, respectively, and new Pd-C(1) and Pd-C(2) bonds were formed. The ∆G^‡ values of the reaction (9 → 10) for Reaction I was calculated to be 2.0 kcal/mol. Additionally, 10 in Reaction I was more stable by 8.3 kcal/mol than 9. Reaction II and III showed these results similar to Reaction I. In reactiton from 10 to 11, 4 dissociates from 10, and a five coordinated intermediate 11 is generated. The geometry changes and relative free energies of this reaction in Reaction I, II and III are shown in Figure 4 and Figure 5, respectively. In this reaction, new Pd-O(1) bond was formed. This reaction proceeds with no barrier, and 11 was more stable by 13.8 kcal/mol than 10 in Reaction I. From these results, it is considered that reaction proceeds. The succeeding isomerization (10 → 11) occurs, to yield a π-aryl complex 12. The ∆G^‡ values of this reaction for Reaction I, II and III were calculated to be 10.4, 10.4 and 13.5 kcal/mol, respectively. Moreover, 12 in Reaction I, II and III were more stable by 10.5, 10.5 and 3.4 kcal/mol than 11, respectively, and this reaction occurs easily.

Scheme 6. Proposed reaction mechanism from 9.

It is considered that the dissociation of 12 gives a product 3 and a mononuclear complex 6. The geometry changes and relative free energies of this reaction in Reaction I, II and III are shown in Figure 6 and Figure 7, respectively. The ∆G^‡ values of this reaction for Reaction I, II and III were calculated to be 10.5, 10.5 and 9.1 kcal/mol, respectively. Finally, the reaction between mononuclear complex 6 and 1 are formed an active species 7, and the catalytic cycle is completed.

We investigated the catalytic cycle starting from 7, as shown in Scheme 7. Figure 8-10 display the relative free energies from 7 in Reaction I, II and III, respectively. The rate-determining step is the nucleophilic attack of carbonyl oxygen to R^A (7→8), their ∆G^‡ values are 27.1, 39.1 and 30.1 kcal/mol, respectively. The ∆G^‡ value of the rate-determining step in Reaction I is lower than that in Reaction II by 12.0 kcal/mol. This result showed the same tendency as the experimental one.

Scheme 7. New acylation reaction with Pd complex.

To investigate in details about these differences, we calculated the C-SiMe₃ and C-SnMe₃ bond energies. The C-SiMe₃ bond energy is stronger than the C-SnMe₃ one by 18.6 kcal/mol. In other words, it is easy to break the C-SnMe₃ bond than the C-SiMe₃ bond. Therefore, it is suggested that Reaction I (R^A = SnMe₃) is more favorable than Reaction II.

On the other hand, since the ∆G^‡ value in Reaction III is lower than that in Reaction II by 9.0 kcal/mol. Since only reactions of Reaction I and II occur in the experiment, this result obtained by our theoretical calculation is different with experimental one. To elucidate this cause, we focused on a formation reaction of the active species. At the first step of the catalytic cycle, 6 reacts with 1 to form the active species 7. 7 in Reaction I and II are more stable than 6 by 2.5 and 1.6 kcal/mol, respectively. On the other hand, 7 in Reaction III is less stable than 6 by 5.2 kcal/mol. From these results, it is suggested that the active species 7 generate only in Reaction I and III. In other words, since the active species 7 in Reaction II does not form, the catalytic reaction cannot proceed. As a result, even if the ∆G^‡ value of the rate-determining step in Reaction II is low, it is considered that the reaction does not occur.

From all results, it is suggested that this catalytic reaction starts from 6 without reaction III and the calculated results well explain the experimental one.

4. Conclusions

In the present study, we investigated the acylation of allylic esters with acylsilanes and acylstannanes in the presence of a palladium complex using the DFT method. Firstly, we examined the reaction mechanism starting from 7. The results of reaction mechanisms are summarized as follows:

1) The O(1) atom of 8 attacks the Sn or Si atom in TS_8-9 to produce 9.

2) The C(1)-C(2) reductive elimination from 9 proceeds through the TS_9-10 to yield 10.

3) 2 attacks 10 to form 11.

4) 11 released 4 to produce a five coordinated intermediate 12.

5) 12 changes into structure to another π-acyl complex 6.

6) The product 3 was released from 6 and 7 forms again for another catalytic cycle.

The rate-determining step is the nucleophilic attack of carbonyl oxygen to R^A (7→8), their ΔG^‡ values are 27.1, 39.1 and 30.1 kcal/mol, respectively.

Therefore, we illustrated three kinds of reactions by the difference in the substituents (R^A and R^B).

Cite this paper

ShoheiSanada,MichinoriSumimoto,KenjiHori, (2015) Theoretical Study on Pd-Catalyzed Acylation of Allylic Esters with Acylsilanes and Acylstannanes. International Journal of Organic Chemistry,05,246-255. doi: 10.4236/ijoc.2015.54024

References

NOTES

^*Corresponding authors.