Journal of Analytical Sciences, Methods and Instrumentation
Vol.04 No.02(2014), Article ID:47298,7 pages
10.4236/jasmi.2014.42009
A New Approach to Carbonate Alkalinity
Bogusław Pilarski1, Anna M. Michałowska-Kaczmarczyk2, Agustin G. Asuero3, Agnieszka Dobkowska1, Monika Lewandowska1, Tadeusz Michałowski4*
1CERKO Sp. z o.o. Sp. K., Gdynia, Poland
2Department of Oncology, The University Hospital in Cracow, Cracow, Poland
3Department of Analytical Chemistry, The University of Seville, Seville, Spain
4Faculty of Engineering and Chemical Technology, Cracow University of Technology, Cracow, Poland
Email: *michalot@o2.pl
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 25 April 2014; revised 26 May 2014; accepted 8 June 2014
ABSTRACT
The article provides experimental data applied to the determination of carbonate alkalinity (CAM) according to modified Gran II functions.
Keywords:
Carbonate Alkalinity, pH Titration, mathematical modelling

1. Introduction
In the papers [1] [2] published recently, the new approaches to the measurement of total alkalinity (TAL) and carbonate alkalinity (CAM) were presented. In particular, CAM refers to titrimetric analysis of two systems (V0 mL): NaHCO3 (C01) + Na2CO3 (C02) (System I), and Na2CO3 (C02) + NaOH (Cb) (System II). The results {(Vj, pHj)│j = 1, …, N} obtained from pH titration of the corresponding systems with C mol/L HCl, undertaken under isothermal conditions, are presented according to a modified Gran II method. The CAM concept is fully compatible with the TAL concept, in which other species with acid-base properties are also included.
The equivalence volumes Veqi (i = 1, 2, 3) referring to the corresponding components in Systems I and II are involved in the following relationships:
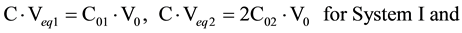 (1)
(1)
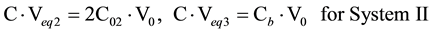 (2)
(2)
Subsequently, the carbonate alkalinities (CAM, mmol/L) are calculated from the formulae: CAM(I) = 103∙(C01 + 2C02) or CAM(II) = 103∙(2C02 + Cb), i.e.,
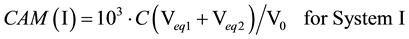 (3)
(3)
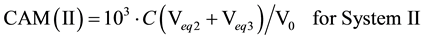 (4)
(4)
The present paper provides a new approach to the problem in question. This approach enables equivalence volumes (Veqi) to be calculated and the following physicochemical data to be evaluated: dissociation constants (K1 and K2) of H2CO3, the ionic product of water (KW), and the activity coefficient (γ) of hydrogen ions―not only in aqueous media, but also in binary-solvent systems [3] . The functions derived for this purpose have a form similar to those ascribed to Gran II method. The validity of the models proposed was confirmed experimentally by pH titration of synthetic samples referring to Systems I and II.
2. The Gran-type Functions
The Gran functions applicable for determination of CAM(I) (Equation (3)) and CAM(II) (Equation (4)) are detailed in Table 1 [2] . The notations applied there are as follows: ph = −logh, h = γ・[H+] - activity, and γ - the activity coefficient of hydrogen ions;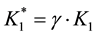 ,
, 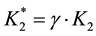 ,
, 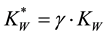 - hybrid values for K1 = [H+][
- hybrid values for K1 = [H+][ ]/[H2CO3], K2 = [H+][
]/[H2CO3], K2 = [H+][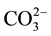 ]/[
]/[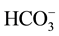 ], and KW = [H+][OH−]. The pH intervals, in which the corresponding Gran-like functions are valid, are denoted by b, c, d for System I, and by a, b, c, d for System II.
], and KW = [H+][OH−]. The pH intervals, in which the corresponding Gran-like functions are valid, are denoted by b, c, d for System I, and by a, b, c, d for System II.
Interval a is not included in System I in Table 1; simply because the data {(Vj, pHj) | j = 1, …, N} do not cover this pH range in System I. Regarding System II, the experimental points may not cover interval a at lower Cb values.
The case where V0 mL of C02 mol/L Na2CO3 is titrated with V mL of C mol/L HCl is a particular case of System I (at C01 = 0) or System II (at Cb = 0). Note that the formulae related to Systems I and II are identical in pH intervals d and c (see Table 1), but the formulae are different in interval b. However, at Vb = Veq1 = 0 and Va = Veq3 = 0, both formulae are simplified into the following form:
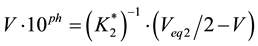 (5)
(5)
In the data handling step referring to simulated or experimental data {(Vj, pHj) | j = 1, …, N}, the Gran functions are applied to the sequences of pH intervals, such as those specified in Table 1. The use of other possible sequences is not advised.
The parameters:
・ Veq1, Veq2, K1*, K2* and γ (and then K1 = K1*/γ, K2 = K2*/γ) for the modified Gran functions referring to System I, or
・ Veq2, Veq3, K1*, K2* and γ (and then K1 = K1*/γ, K2 = K2*/γ) for the modified Gran functions referring to System II,
can be found according to the least squares method (LSM) [4] [5] applied to the experimental points:
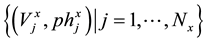
referring separately to particular x intervals: x = b, c, d (System I), or x = a, b, c, d (System II) in Table 1, with the set of Nx points, related to the x-th pH interval. It is worth noting that the ph, referring to activity h of H+ ions, is measured in experimental titrations. The ph = −logh as variable (not pH = −log[H+]) is involved in all relationships specified in Table 1.
3. Calculation Procedure
The functions in Table 1 can be presented in a unified form of the linear regression equation:
Table 1. The Gran functions related to Systems I and II.
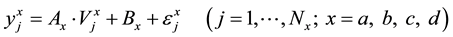 (6)
(6)
Subsequently, applying LSM to the sum of squares
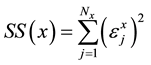 (7)
(7)
where j refers to the points 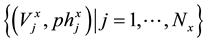 related to x-th subset (x = a, b, c, d), we obtain the formu-
related to x-th subset (x = a, b, c, d), we obtain the formu-
lae:

where the sum 

interval.
As stated above, calculation of the parameters is possible in a defined sequence of operations. For example, the sequence d → c applied in Table 1 for System I means that Vd value, obtained according to LSM for the
data 
on the left side of the relationship referring to interval c and LSM is applied to the data

calculate:




Moreover, we obtain:



From Table 1, System I, no. b, for the point 


Figure 1. Plots related to NaHCO3 (C1) + Na2CO3 (C2) system: y (Table 1, System I) vs V relationships in (a) d interval; (b) c interval; (c) 


where Veq1 and Veq2 are expressed by Equation (1). Similarly, from Table 1, System II, no. b and a, we get


respectively, where Veq2 and Veq3 are expressed by Equation (2). On the basis of Equation (5), we obtain the relationship:

We then calculate:


and

where γ is defined in Equation (11). The nearly constant ionic strength value, required during the titration, can be secured by the addition of a basal electrolyte on the stage of D and T preparation.
As revealed from Equations (3), (4), it is necessary to know the sum of equivalence volumes: Veq1 + Veq2 or Veq2 + Veq3, to calculate CAM(I) or CAM(II) value. However, determination of Veqi values (i = 1, 2 or 2, 3) from a single pH titration curve is also possible.
4. Experimental part
4.1. Apparatus and Solutions
The pH titrations were carried out in a 30 mL thermostated, self-made measuring cell, equipped with magnetic stirrer and PT 1000 temperature sensor. The pH measurements and titrations were taken at 22˚C with a Cerko Lab System microtitrator, equipped with 5 mL syringe pump, 3-way valve, and pH electrode (Hydromet, type ERH-13-6). The electrode was standardized with aqueous standard buffers of pH 5.00, 7.00 and 10.00, purchased from the Chempur Company. When not in use, the electrode was stored in 3 mol/L KCl solution. Titrant was added into V0 = 4.00 mL of D stepwise, in aliquots of 0.01 mL, with 6-8-sec. pauses, and the experimental
points 
The reagents: HCl, Na2CO3, NaHCO3, NaOH of p.a. grade, purchased from Chempur Company, were used for the preparation of stock and diluted solutions in doubly distilled (freshly prepared, with conductivity of approx. 0.18 μS/cm) water. Stock solution of hydrochloric acid (HCl) as T, was standardized against Na2CO3, obtained after prior calcination (220˚C, 5 hrs) of commercial disodium carbonate. The NaOH solution was standardized against potassium hydrogen phthalate (p.a., from Merck). Methanol (p.a. grade, 99.5%, supplied by POCH S.A.) was applied for titrations made in binary-solvent media.
Stock titrands were prepared by dilution of weighed portions of Na2CO3 and NaHCO3 in water, or by addition of a weighed portion of Na2CO3 into a standardized NaOH solution. In other titrations, mixed solvent was prepared from appropriate volumes of water and CH3OH, and cooled before preparation of HCl and Na2CO3 solutions. The HCl solution (10% v/v CH3OH) was standardized as described previously. Concentrations of HCl, NaHCO3, Na2CO3 and NaOH in the corresponding solutions are specified below.
4.2. Results and Discussion
The approach was applied first to the results of titrations of Systems I and II, with HCl solution as the titrant, T. Titration in System I was carried out at pre-assumed values (V0, C01, C02, C) = (4.000, 0.01012, 0.02011, 0.10078); Veq1 = 0.01012・4/0.10078 = 0.4017; Veq2 = 2・0.02011・4/0.10078 = 1.5963. The results of exemplary titration are graphically presented in Figure 1. The data obtained for Vd = 2.0122, Vc = 0.8017 (Figure 1(a), Figure 1(b)) are in good agreement with the expected values: 1.9980 and 0.7982 (see Table 2). Moreover, we get here: γ = 0.9283 and 
Titration in System II was carried out at pre-assumed values (V0, C02, Cb, C) = (4.000, 0.0200, 0.0209, 0.10078). The results obtained from repeated titrations are detailed in Table 3; 2・0.0200・4/0.10078 = 1.5876 and 0.0209・4/0.10078 = 0.08295 are the expected values for Veq2 and Veq3, respectively. Exemplary data are plotted in Figure 2. As can be seen, the sum Vd = Veq2 + Veq3 is very well reproducible in repeated titrations and is in good agreement with the expected value of 2.4171 (Figure 2(a)). The values for Veq2 are slightly smaller than 1.5876, while the values for Veq3 are slightly greater than 0.08295. The repeatability of values for γ and 






Another option for System II is also possible a priori and starts from equation a in Table 1 (System II) and
finds Va (=Veq3) and 

equation b in Table 1 (System II) and Vb (=Veq2/2 + Veq3) and 


Figure 2. Plots related to Na2CO3 (C2) + NaOH (Cb) system: y (Table 3) vs. V relationships in (a) d interval; (b) c interval; (c) 

points
on the basis of the experimental points in intervals d and c. This procedure could be regarded as a kind of internal validation of the results. However, it should be borne in mind that the results of ph measurements obtained in alkaline media could be loaded by systematic error resulting from the alkaline error of the glass electrode. The errors involved with ph measurements in the a range affect the Va value, subsequently applied in the (V − Va)・10ph vs. V relationship related to interval b; an improper Va value causes this relationship to be a nonlinear one. Therefore, it is advisable to use the experimental points from interval b (for System I) or from intervals a and b (for System II) only for the determination of the related equilibrium parameters, see Equations (12)-(18).
On the basis of known values for Vd found in interval d for Systems I and II (see Table 1), the alkalinities: CAM(I) (Equation (3)), and CAM(II) (Equation (4)) can be calculated; obtaining:
CAM(I) = 0.10078・2.0122/4 = 0.0507 (from Table 2, no. 1),
CAM(II) = 0.10078・2.4123/4 = 0.0608 (from Table 3, no. 3).
5. Final comments
This article provides the new consistent formulation for alkalinities referring to NaHCO3 + Na2CO3 (System I) and Na2CO3 + NaOH (System II) solutions, titrated with HCl. The related formulae, specified in Table 2, are valid in defined pH intervals, denoted as b, c, d or a, b, c, d. The approach based on these new formulae has been called “carbonate alkalinity in a modified version” (CAM). All the formulae are closely relevant to the recently formulated total alkalinity (TAL) [1] [2] . The formulae for CAM are valid within defined pH ranges, in which the relationships between variables are expressed by the functions specified in Table 1.
The CAM approach enables equivalence volumes to be calculated, as well as the following physicochemical data: the activity coefficient (γ) of hydrogen ions; the hybrid values for dissociation constants:


The pH-intervals assumed for calculation of the analytical and physicochemical data are confined (see [2] , p. 229) in comparison with the ones pre-assumed with use of the D = 1.9 value. The narrowing of the pH-range taken for calculations results from the scale of (C01, C02, C) or (C02, C03, C) values applied in the experiments.
The procedure applied here can also be extended to salts other than carbonates. To extend the pH range covered by pH titration, it is suggested that the option involving the addition of a pre-dose is used [2] . When weak acid is considered, the strong base solution can be used as titrant or, after addition of the base as the pre-dose, the mixture can be titrated with a strong acid, as above.
The CAM method was tested experimentally. The results for the dissociation constants of H2CO3 are close to those found in literature [7] . The values for γ are more scattered.
This article attempts to provide an introductory step for further studies about the determination of alkalinity
Table 2. Results obtained from repeated titrations made in System I.
Table 3. Results obtained from repeated titrations made in System II.
according to the proposed TAL method [1] [2] for examination of natural, municipal and industrial waters, carbonated soft drinks and wines, as well as different biological systems.
The CAM presented here completes the list of modifications of the Gran methods presented in previously published articles [8] - [12] , referring to different areas of titrimetric analysis.
References
- Asuero, A.G. and Michałowski, T. (2011) Comprehensive Formulation of Titration Curves Referred to Complex Acid-Base Systems and Its Analytical Implications. Critical Reviews in Analytical Chemistry, 41, 151-187. http://dx.doi.org/10.1080/10408347.2011.559440
- Michałowski, T. and Asuero, A.G. (2012) New Approaches in Modelling the Carbonate Alkalinity and Total Alkalinity. Critical Reviews in Analytical Chemistry, 42, 220-244. http://dx.doi.org/10.1080/10408347.2012.660067
- Pilarski, B., Dobkowska, A., Foks, H. and Michałowski, T. (2010) Modeling of Acid-Base Equilibria in Binary-Sol- vent Systems: A Comparative Study. Talanta, 80, 1073-1080. http://dx.doi.org/10.1016/j.talanta.2009.07.033
- Sayago, A., Boccio, M. and Asuero, A.G. (2004) Fitting Straight Lines with Replicated Observations by Linear Regression: The Least Squares Postulates. Critical Reviews in Analytical Chemistry, 34, 39-50. http://dx.doi.org/10.1080/10408340490273744
- Asuero, A.G., Sayago, A. and González, A. (2006) The Correlation Coefficient: An Overview. Critical Reviews in Analytical Chemistry, 36, 41-59. http://dx.doi.org/10.1080/10408340500526766
- Michałowski, T., Pilarski, B., Asuero, A.G., Dobkowska, A. and Wybraniec, S. (2011) Determination of Dissociation Parameters of Weak Acids in Different Media According to the Isohydric Method. Talanta, 86, 447-451. http://dx.doi.org/10.1016/j.talanta.2011.09.002
- Inczédy, J. (1976) Analytical Applications of Complex Equilibria. Horwood, Chichester.
- Michałowski, T., Baterowicz, A., Madej, A. and Kochana, J. (2001) An Extended Gran Method and Its Applicability for Simultaneous Determination of Fe(II) and Fe(III). Analytica Chimica Acta, 442, 287-293. http://dx.doi.org/10.1016/S0003-2670(01)01172-2
- Michałowski, T., Toporek, M. and Rymanowski, M. (2005) Overview on the Gran and Other Linearization Methods Applied in Titrimetric Analyses. Talanta, 65, 1241-1253. http://dx.doi.org/10.1016/j.talanta.2004.08.053
- Michałowski, T., Kupiec, K. and Rymanowski, M. (2008) Numerical Analysis of the Gran Methods. A Comparative Study. Analytica Chimica Acta, 606, 172-183. http://dx.doi.org/10.1016/j.aca.2007.11.020
- Ponikvar, M., Michałowski, T., Kupiec, K., Wybraniec, S. and Rymanowski, M. (2008) Experimental Verification of the Modified Gran Methods Applicable to Redox Systems. Analytica Chimica Acta, 628, 181-189. http://dx.doi.org/10.1016/j.aca.2008.09.012
- Michałowski, T., Pilarski, B., Ponikvar-Svet, M., Asuero, A.G., Kukwa, A. and Młodzianowski, J. (2011) New Methods Applicable for Calibration of Indicator Electrodes. Talanta, 83, 1530-1537. http://dx.doi.org/10.1016/j.talanta.2010.11.067
Symbols used
CAM―carbonate alkalinity [mmol/L] in modified version;
D―titrand (solution titrated);
γ = h/[H+]―activity coefficient for H+ ions;
h―activity of H+ ions;
LSM―least squares method;
pH = −log[H+];
ph = −logh;
T―titrant;
TAL―total alkalinity;
V―volume [mL] of T;
V0―volume [mL] of D;
Veqi―volume [mL] of titrant, referring to the equivalence point (Veqi, pHeqi);
[X]―concentration [mol/L] of the species X.
NOTES
*Corresponding author.



