Int'l J. of Communications, Network and System Sciences
Vol.1 No.3(2008), Article ID:110,7 pages DOI:10.4236/ijcns.2008.13027
Joint Adaptive Modulation and Power Allocation in Cognitive Radio Networks
School of Information and Science Technology, Sun Yat-Sen University, Guangzhou, China
E-mail: lid3@mail2.sysu.edu.cn
Received on May 4, 2008; revised and accepted on August 25, 2008
Keywords: Adaptive Modulation, Power Allocation, Cognitive Radio
Abstract
Link adaptation is an important issue in the design of cognitive radio networks, which aims at making efficient use of system resources. In this paper, we propose and investigate a joint adaptive modulation and power allocation algorithm in cognitive radio networks. Specifically, the modulation scheme and transmit power are adjusted adaptively according to channel conditions, interference limit and target signal-to-interference-plus-noise ratio (SINR). As such the total power consumption of cognitive users (CUs) is minimized while keeping both the target SINR of CUs and interference to primary user (PU) at an acceptable level. Simulation results are provided to show that the proposed algorithm achieves a significant gain in power saving.
1. Introduction
With the increasing number of various bandwidth-consuming wireless services, spectrum for available bands becomes more and more scarce. Moreover, these bands are not occupied or underutilized by licensed users most of time, which leads to the waste of bandwidth resources and low spectral efficiency. One solution to this problem is that cognitive (unlicensed) users (CUs) are allowed to have opportunistic access to these idle bands or to the active ones without causing harmful interference to the primary (licensed) user (PU), in order to improve the bandwidth utilization. This technology is called cognitive radio [1,2]. The major advantage of cognitive radio technology is its ability to search for available spectrums in its surrounding environment and adjust its transmit parameters accordingly to enhance the system performance. The transmit parameters, for example, include modulation scheme, beamforming vector, center frequency, transmit power and so on. The whole process can be summarized as “sense-cognition-adaptation”.
In wireless network, a fundamental characteristic is the interference introduced by multi-user or co-channel transmission at the same time or over the same frequency radio channel. It is well-known that power allocation [3,4] is an effective way to mitigate interference by means of updating transmit powers according to the target SINR. Besides, the effective use of transmit power can not only minimize the interference introduced by other transmit nodes to enhance the capacity, but also conserve energy to prolong battery life. In [3], the author proposed a simple distributed power allocation algorithm, in which the power level at next iteration only depends on target and actual SINR as well as current power level. The goal is to minimize the total power consumption subject to the target SINR requirement. Further studies are shown in [5–8]. In [5], the joint optimization of beamforming and power control is studied in the downlink of a cognitive radio network. The objective of the proposed algorithm is to minimize the total transmit power while satisfying the target SINR constraint of CUs and maximum tolerable interference to PU. However, this work can not be extended to the energy-constrained wireless networks, in which there is a constraint of maximum transmit power for each CU. Literature [6] proposes a cross-layer framework for joint scheduling and power control combined with adaptive modulation in ad hoc networks, which can be viewed as the situation where only CUs share the same frequency band with the absence of PU. Therefore, the proposed algorithm can not be applicable to the case of the co-existence of PU and CUs in the same frequency band, since it does not consider the interference introduced to PU caused by CUs. While literature [7] and [8] only consider the problem of adaptive modulation and power control of a single CU in the presence of PU.
In contrast to previous work in [5–8], we consider the scenario where one PU and multiple CUs share the same frequency band in wireless networks. So far as we know, little attention has been paid to the topic of joint adaptive modulation and power allocation in cognitive radio networks, in which the protection of PU and the quality of service (QoS) of CUs are assured. In this contribution, our goal is, therefore, to jointly optimize the modulation schemes as well as transmit powers in order to minimize the total power consumption while keeping both the interference to PU and target SINR of CUs at an acceptable level. More specifically, we perform a two-stage power allocation processing for the proposed algorithm: First, transmit powers are allocated to all CUs with the same modulation scheme, under the constraint of target SINR of CUs and a given interference limit to PU; Second, each CU with adaptive modulation scheme adjusts its transmit power based on the first allocated power, in order to reduce the total power consumption.
The rest of this paper is organized as follows: Section 2 describes the system model and basic assumptions. In Sections 3, we develop the proposed algorithm for joint adaptive modulation and power allocation in cognitive radio networks. Performance analysis of the proposed algorithm is investigated in Section 4. Section 5 concludes this paper.
Notation: All vectors and matrices are denoted in bold letters.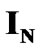 
stands for
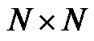identity matrix. 
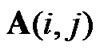denotes the 
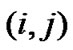th element of the matrix
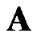. The operators
, 
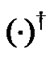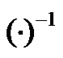and 
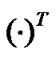represent pseudo inverse, inverse and transpose, respectively.
Figure 1. System model with one PU in dashed line and N CUs in solid line.
2. System Model
The cognitive radio network under consideration is composed of one PU and N CUs, which are modeled as a collection of separate (N+1) transmit-receive pairs with a single channel, as illustrated in Figure 1. All CUs are allowed to transmit at the same time and share the same frequency band by adopting code division multiplexing access (CDMA). The transmission mode for each CU is half-duplex in order to avoid self-interference [9] caused by one node simultaneously transmitting and receiving. The channel propagation model is characterized by path loss, which is given by [10]
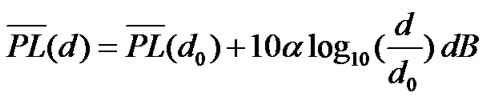
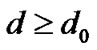(1)
where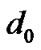 
and 
are the reference and transmitter-receiver (T-R) distance, respectively.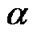 
denotes path loss exponent, which depends on propagation circumstance.
Then, the actual SINR for ith CU can be expressed as
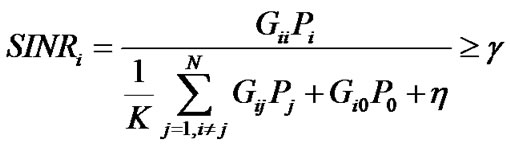(2)
where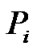 
and 
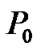denote power level of ith CU and primary user, respectively. 
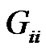is the channel gain over CU i, 
and 
represent the channel gain between CU j’ transmitter, primary user’s transmitter and CU i’ receiver, respectively. 
is the background noise power and K denotes the spreading gain.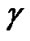 
is the target SINR for all CUs and the constraint 
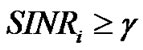guarantee the QoS for ith CU. On the other hand, the total interference introduced to PU is given by
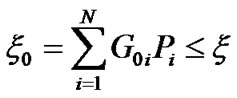(3)
where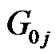 
represents the channel gain between CU j’ transmitter and PU’s receiver and 
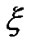denotes the maximum tolerable interference for PU.
Throughout this paper, we make the following assumptions:
1) The system consists of an access point (AP) [11] for dialogues with CUs through a dedicated control channel, and the global information of channel gains is assumed to be available at AP.
2) The local information of channel gains and SINR measurements at the receivers of all CUs are sent to their respective transmitters via a dedicated feedback channel.
3) All CUs are well synchronized, and are assumed to be immobile or move slowly so that the corresponding channel gain remains constant during the convergence of transmit power.
3. Joint Adaptive Modulation And Power Allocation
The objective of this algorithm is to assign constrained transmit powers and available modulation schemes to all CUs, in order to minimize the total power consumption while satisfying the target SINR constraint of CUs. Besides, we should also consider maintaining the interference introduced to the primary user within a given interference limit, since CUs coexist with the PU in the same frequency band. Therefore, we can formulate the following constrained optimization problem:
minimize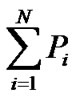 
(4)
subject to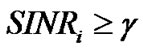 
(5)
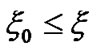(6)
where 
and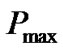 
is the maximum transmit power.
In what follows, transmit powers which satisfy both the constraint (5) and (6) are calculated by AP and sent to all CUs, in which the modulation scheme is the same and chosen to guarantee the existence of positive powers. Then, the modulation scheme (or equivalently, target SINR) is modified based on the initial SINR for each CU, in order to maintain a certain BER requirement. It will be shown that, based on the modified target SINR for each CU, the total power consumption is greatly reduced by iteratively updating transmit power of each CU, while both the QoS and interference constraint can also be satisfied.
3.1. First Power Allocation
The constraint (5) can be expressed in the following way
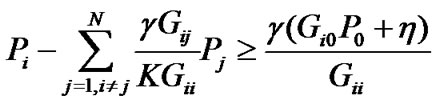(7)
Note that the target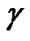 
is the same for all CUs in this stage. Let
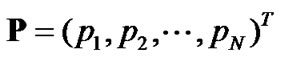, rewrite (7) with equality in the matrix form, we can obtain
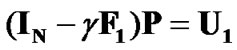(8)
where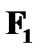 
and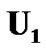 
are given by in the following
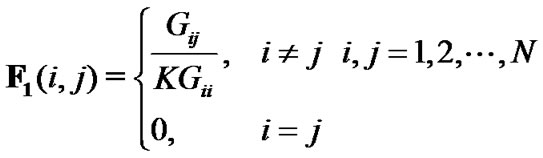
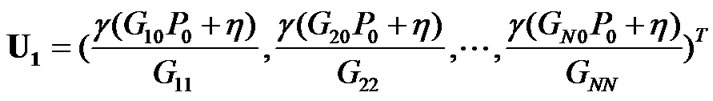
Meanwhile, we can also rewrite constraint (6) with equality in the matrix form as
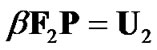(9)
where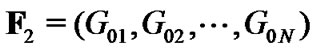 
is a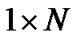 
vector and
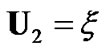. Note that, in equation (9), 
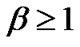is a constant, and the interference constraint of PU can be easily satisfied by increasing the value of
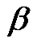, because the powers allocated to all CUs are kept at a low level. However, it does not mean that large 
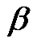will satisfy the target SINR requirement for all CUs. Combine (8) and (9), the constraints (5) and (6) can be finally expressed in the matrix form as follows
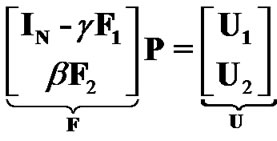(10)
where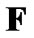 
is a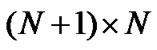 
matrix and 
is a 
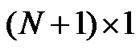column vector. Note that the equation (10) has a feasible solution, i.e., there exists a positive power vector
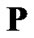, if the following condition holds
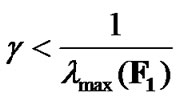(11)
where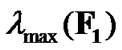 
stands for the maximum eigenvalue of matrix
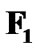. Otherwise, no CUs can be admitted to share this frequency band with PU. As for the value of
, we will give details in the next section. Once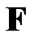 
and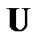 
are determined, the powers first allocated to CUs are given by
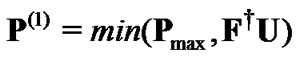(12)
where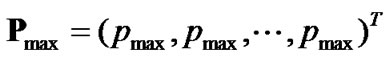 
is a 
column vector and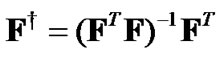
.
Remarks:
1) Equation (10) is overdetermined, and (12) is its least square (LS) solution to the optimization problem of (4) with constraints (5) and (6).
2) The first allocated transmit powers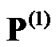 
and fixed modulation scheme (or
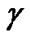) are obtained at AP, and this information is sent from AP to the transmitter of corresponding CU through the dedicated control channel.
Table 1. Constellation size and corresponding minimum required SINR for target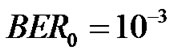 
[6].
It should be noted that the protection of PU and QoS of CUs are both met without the maximum power constraint. However, due to the fact of power-constrained CUs, the target SINR constraint of all CUs may not be satisfied. In the following, we will address this issue in detail.
3.2. Adaptive Modulation
Adaptive modulation enables the system to support high data rate by varying the number of bits per symbol in accordance with the instantaneous SINR, while keeping a target BER requirement. The transmission rate of ith CU for M-ary quadrature amplitude modulation (M-QAM) is given by [6]
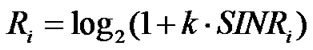(13)
where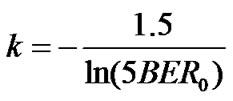 
and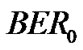 
is the target BER requirement. Note that transmission rate obtained in equation (13) is contiguous and should be quantized to a finite number of integer values in practical situation. The minimum required SINR corresponding to the target 
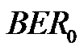for M-QAM can be obtained by [6]
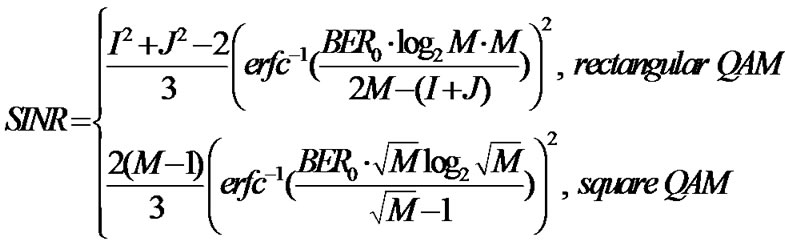(14)
where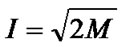 
and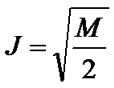
. As a result, the minimum required SINRs corresponding to 
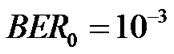for M = 2, 4, 6, 8, 16, 32 and 64 can be calculated and the results are shown in Table 1.
According to Table 1,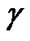 
is determined in such a way that the maximum SINR is chosen from available ones which satisfy the condition (11), in order to achieve high data rate. However, the actual SINR based on the initial allocated power for each CU can not satisfy the minimum required SINR for certain 
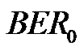at the same time. Therefore, the modulation scheme, i.e. target SINR
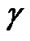, should be modified for each CU. To be specific, assuming that the set 
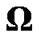is composed of SINRs in Table 1 which are no more than
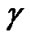, then the modified target SINR for each CU denoted as
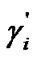, is chosen in such a way that the corresponding required SINR in 
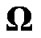is no more than its actual SINR. In the worst case, if the actual SINR falls below 4.77, the corresponding CU will abort transmission. For instance, if 
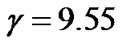and the CUs’ actual SINRs based on the first allocated powers are 10, 5 and 3, respectively, then
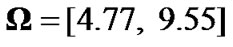, and therefore
, 
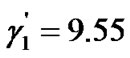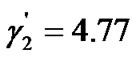and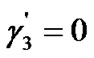 
(no transmission), respectively. Note that, in this case, the constraint (5) is changed into
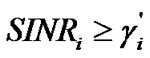. Therefore, the modified target SINR constraint of all CUs can be satisfied.
3.3. Second Power Allocation
Since both the QoS and interference constraint are satisfied as discussed before, we consider reducing the total power consumption for all CUs. Let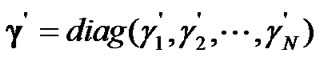 
be a diagonal matrix of size
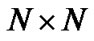, then the equation (8) can be rewritten in the following form as
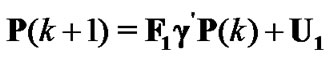(15)
where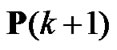 
and 
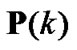denote power level at next and current iteration, respectively. Then, the optimal transmit power can be obtained by iteration of [3]
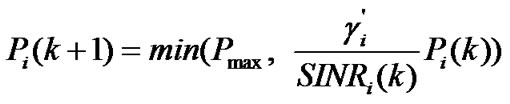(16)
Note that the above algorithm terminate with convergent power if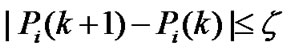
, where 
is a negligibly small error. Based on 
and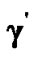
, it can be known that the total power consumption will be reduced after second power allocation using equation (16), in which the initialized power is
. The following theorem supports our conclusion.
Theorem: Given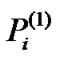
and corresponding 
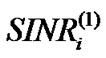which satisfy
, 
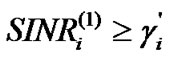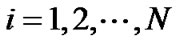, then there exists a steady-state
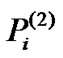to achieve 
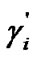such that
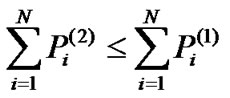while satisfying both the QoS and interference constraint.
Proof: It can be known from equation (16) that, if SINR for each CU satisfies the condition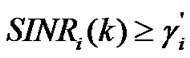
, then we have
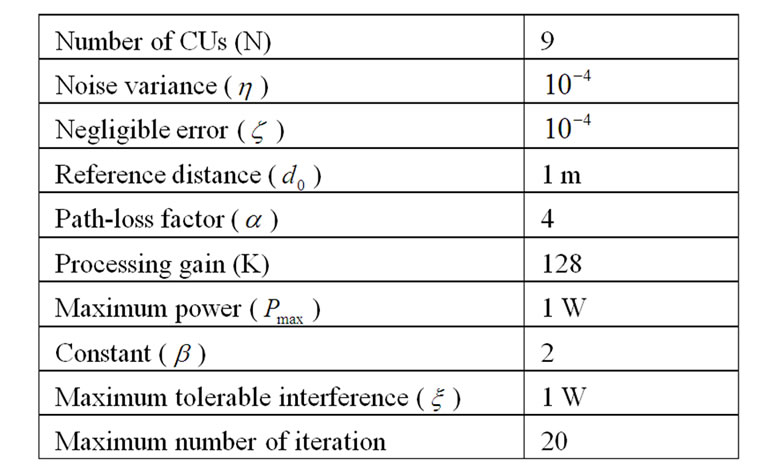
Table 2. Simulation parameters.
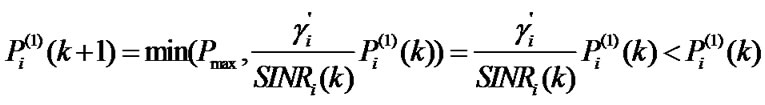
The iteration will terminate if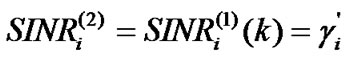
, so the QoS constraint of CUs is satisfied. That is to say that there is no negligible change in 
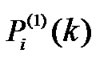such that
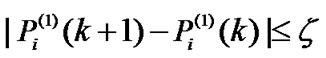. Therefore, the convergent power
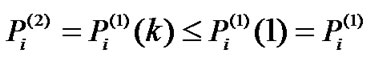. As a result, we have
, and the interference constraint of PU is also satisfied with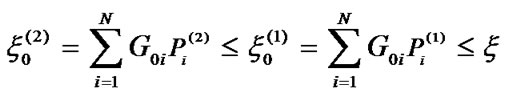
.
4. Simulation Results
In this section, we provide numerical results to demonstrate the effectiveness of the proposed algorithm
(a)
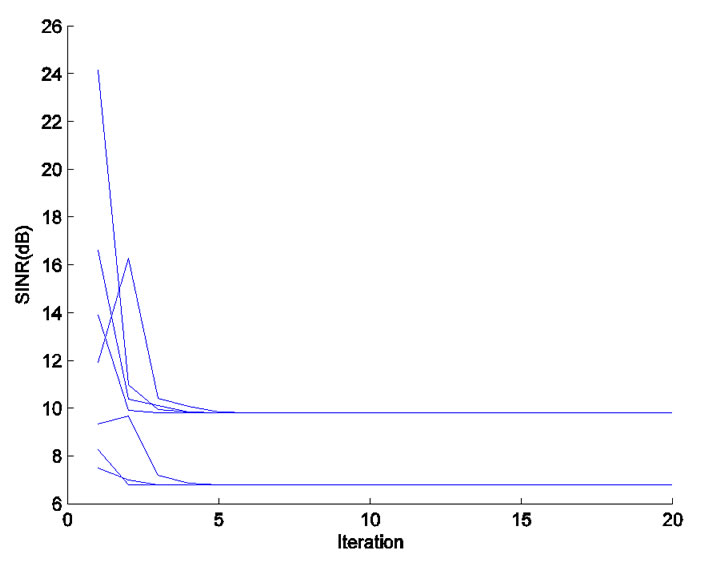(b)
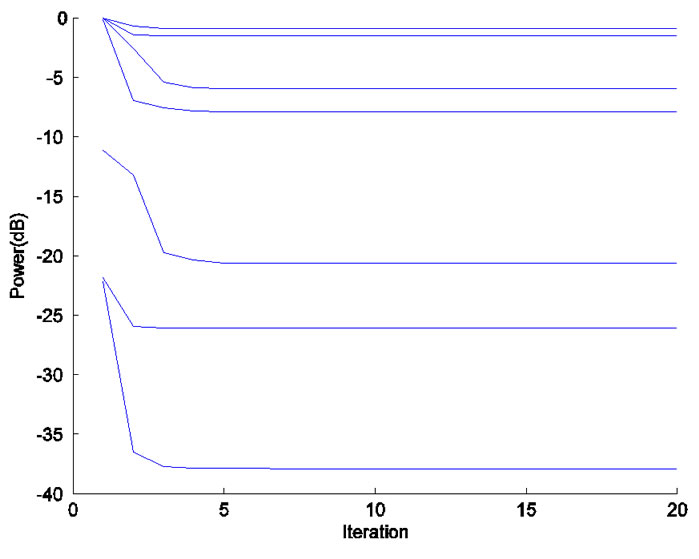
Figure 2. Convergence of transmit power and actual SINR for each CU in the second power allocation stage, where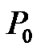 
= 5W. (a) Transmit Power (dB). (b) Actual SINR (dB).
in reduction of the total power consumption while satisfying both the QoS constraint of CUs and interference constraint of PU. Besides, we analyze the effect of different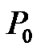 
on the proposed algorithm.
In our simulation, we consider the cognitive radio network placed in a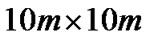 
square area, in which transmit nodes are located uniformly and the corresponding receive nodes are random placed within 
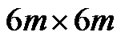square area centered around them. The specific parameters used in this simulation are listed in Table 2, in which the channel gain can be expressed as
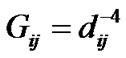, where 
is the distance between jth CU’s transmitter and ith CU’s receiver.
4.1. Performance Analysis
First, we examine the performance of proposed algorithm with respect to power saving. Figure 2(a) shows the convergence property of transmit power for each CU in the second power allocation stage with 
= 5W, in
(a)
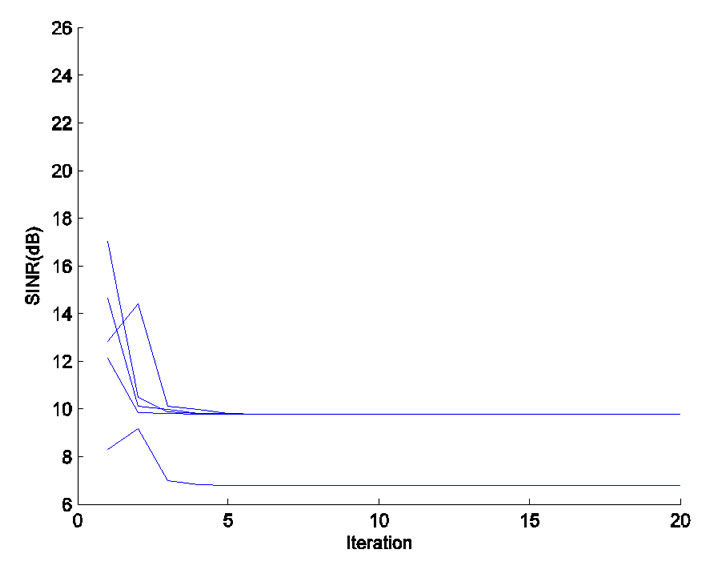(b)
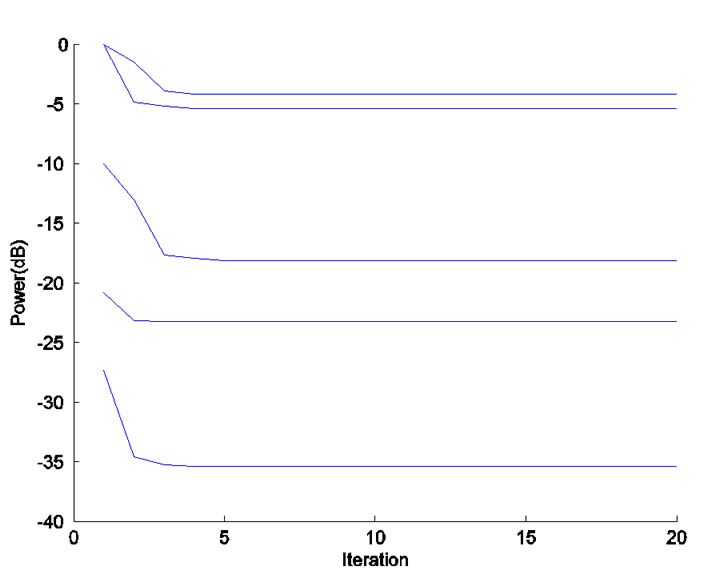
Figure 3. Convergence of transmit power and actual SINR for each CU in the second power allocation stage, where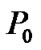 
= 10W. (a) Transmit power (dB). (b) Actual SINR (dB).
which the initial powers are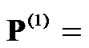 
(1, 1, 0.006, 0.0773, 1, 0.9601, 1, 1, 0.0065) in W according to equation (10), and the convergent powers are 
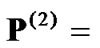(0.8079, 0.2538, 0.0002, 0.0086, 0, 0.1626, 0.7089, 0, 0.0025) in W. From Figure 2(a), we can find that the total power consumption is greatly reduced after second power allocation with adaptive target SINR.
Then, we investigate the SINR performance of the proposed algorithm. Based on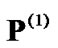
, the actual SINRs for all CUs are 
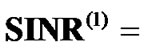(5.6153, 8.5909, 260.7868, 15.5663, 0.1612, 45.7656, 6.6999, 0.0398, 24.4918). 
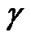is set to be 9.55 so that the constraint (11) is satisfied, and 
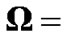(4.77, 9.55). Therefore, the adjusted target SINRs for all CUs in the second power allocation stage are set to be 
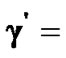(4.77, 4.77, 9.55, 9.55, 0, 9.55, 4.77, 0, 9.55). We notice that the target SINRs of two CUs are equal to 0, which means that the corresponding CU will not transmit. Figure 2(b) shows the convergence property of the actual SINR for each CU, in which the actual SINRs for the admitted CUs converge to 4.77 and 9.55, respectively. In other words, the constellation size M is chosen to be 2 and 4, accordingly.
Finally, we examine the performance of the proposed algorithm in terms of the interference constraint of PU. According to equation (3), the actual interferences introduced to PU in the first and second power allocation stage are 8.8 mW and 4.8 mW, respectively, which are far less than the interference limit 
= 1 W. This is mainly due to the maximum transmit power limit for each CU.
4.2. Impact of Different P0
In our previous study, a constant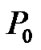 
is chosen for all simulations. To be more practical, we study the impact of different 
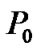on the system performance.
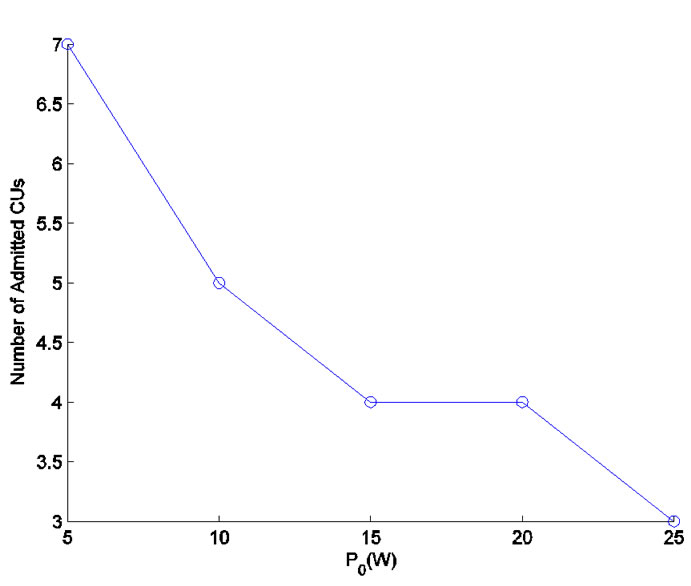
Figure 4. Number of admitted CUs versus P0.
As expected, with the increasing value of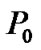
, the interference introduced to all CUs will increase accordingly. This means the first allocated power 
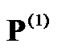will be increased for each CU in order to satisfy the target SINR constraint. For instance in Figure 3(a), 
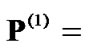(1, 1, 0.0018, 0.1003, 1, 1, 1, 1, 0.0082) in W. Besides, the convergent powers are 
(0, 0.3813, 0.0003, 0.0153, 0, 0.2909, 0, 0, 0.0048) in W.
Meanwhile, the increased interference caused by PU will certainly affect the SINR performance for each CU. In this case, the SINR constraint of some CUs will be violated. Therefore, the initial SINRs of these CUs decrease and corresponding target SINRs should be adjusted accordingly, which can be seen from Figure 3(b). In Figure 3(b), we can find that two CUs’ target SINRs are reduced from 4.77 to 0 compared with Figure 2(b). That is to say these CUs abort transmission. Specifically in Figure 3(b), the actual SINRs for all CUs are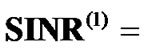 
(2.9760, 6.7423, 50.5086, 19.2122, 0.1538, 29.2723, 3.3640, 0.0204, 16.3146), 
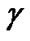= 9.55 and 
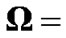(4.77, 9.55). Therefore, the adjusted target SINRs for all CUs in the second power allocation stage are 
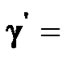(0, 4.77, 9.55, 9.55, 0, 9.55, 0, 0, 9.55).
Furthermore, A close observation of Figure 2 and Figure 3 shows that the convergence of transmit power and actual SINR for each CU requires only several iterations with different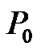
, which is quite acceptable.
As mentioned before, some CUs are turned off in the second power allocation stage, in which their QoS can not be guaranteed due to the interference from PU. It would be also interesting to study the relationship between the number of admitted CUs and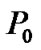
. As can be seen from Figure 4, the number of accepted CUs decreases with the increasing value of 
in general. This is because more CUs’ QoS requirements can not be satisfied and switched off accordingly. In this case, the total power consumption after second power allocation decreases roughly with the decreasing number of admitted CUs. However, we also notice that the number of admitted CUs remains the same for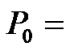 
15 and 20 W, which means more power consumption is needed when 
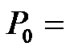20W than the case of 
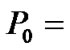15W. It can be known that, when 
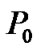is large enough, there is no CUs that can be admitted by the system.
5. Conclusions
In this paper, we have proposed and investigated a joint adaptive modulation and power control algorithm in cognitive radio networks. Our goal is to minimize the total power consumption while keeping the interference introduced to PU below a given limit and satisfying the SINR constraint of CUs. Specifically, the proposed algorithm is implemented in a two-stage power allocation processing with fixed and adaptive modulation, respectively, which has been proved to greatly improve the power efficiency. Simulation results are shown to confirm the effectiveness of the proposed algorithm.
6. Acknowledgement
This work is supported by the National Science Foundation of China (NSFC), Grant 60772132, and the joint foundation of National Science Foundation of China (NSFC) and Guangdong Province U0635003, and also supported by the Science & Technology Project of Guangdong Province, Grant 2007B010200055.
7. References
[1] S. Haykin, “Cognitive radio: brain-empowered wireless communications,” IEEE Journal on Selected Areas in Communications, Vol. 23, No. 2, pp. 201–220, February 2005.
[2] J. Mitola, “Cognitive radio: an integrated agent architecture for software defined radio,” Tekn. Dr. dissertation, Royal Institute of Technology (KTH), Stockholm, Sweden, 2000.
[3] G. J. Foschini and Z. Miljanic, “A simple distributed autonomous power control algorithm and its convergence,” IEEE Transactions on Vehicular Technology, Vol. 42, No. 4, pp. 641–646, November 1993.
[4] J. Huang, R. A. Berry, and M. L. Honig, “Distributed interference compensation for wireless networks,” IEEE Journal on Selected Areas in Communications, Vol. 24, No. 5, pp. 1074–1084, May 2006.
[5] M. H. Islam, Y. C. Liangand, and A. T. Hoang, “Joint beamforming and power control in the downlink of cognitive radio networks,” in Proceedings IEEE Wireless Communications and Network Conference, pp. 21–26, March 2007.
[6] W. L. Huang and K. B. Letaief, “Cross-layer scheduling and power control combined with adaptive modulation for wireless ad hoc networks,” IEEE Transactions on Communications, Vol. 55, No. 4, pp. 726–739, April 2007.
[7] M. Hong, J. Kim, H. Kim, and Y. Shin, “An adaptive transmission scheme for cognitive radio systems based on interference temperature model,” in Proceedings IEEE Consumer Communications and Networking Conference, pp. 69–73, January 2008.
[8] L. Guo, P. Wu, and S. Cui, “Power and rate control with dynamic programming for cognitive radios,” in Proceedings IEEE Global Telecommunications Conference, pp. 1699–1703, November 2007.
[9] T. ElBatt and A. Ephremides, “Joint scheduling and power control for wireless ad hoc networks,” IEEE Transactions on Wireless. Communications, Vol. 3, No. 1, pp. 74–85, Januray 2004.
[10] T. S. Rappaport, “Wireless communications principles and practice,” Prentice Hall Inc. 1996.
[11] IEEE 802.22 Working Group on Wireless Regional Area Networks, http://www.ieee802.org/22.