 Energy and Power Engineering, 2013, 5, 1490-1496 doi:10.4236/epe.2013.54B282 Published Online July 2013 (http://www.scirp.org/journal/epe) An Alternative Three-phase Transmission Lines Model in Phase Domain C. G. Carvalho1, S. Kurokawa1, J. Pissolato2 1Universidade Estadual Paulista (Unesp), Electrical Engineering Department, Ilha Solteira, Brazil 2Universidade Estadual de Campinas (Unicamp), Electrical Engineering Department, Campinas, Brazil Email: carol.gcarvalho@hotmail.com Received 2013 ABSTRACT The objective of this paper is to show an alternative model of a non-transposed three-phase transmission line with a vertical symmetry plane in phase domain. Due the line physical characteristics, it can be represented by a system consisting of a single-phase and a two-phase line. In this system, the equations describing the behavior of the values in single-phase line terminals are known, while the equations for two-phase line to be obtained. Using a transformation matrix written explicitly according to three-phase line parameters, it is possible to obtain the currents and voltages in phase domain of two-phase line. Then, modal values of three-phase line are converted into phase domain and thus ob- tain the analytical model for this line. To verify the performance of this model, it was used to simulate the energization of a 440 kV three-phase line and the results were compared to results obtained using a classical model. Keywords: Transmission Lines; Frequency Dependence; Modal Representation; Transformation Matrix; Newton-Raphson; Phase Domain 1. Introduction It is known that methods of electromagnetic transient analysis in power systems can consider transmission line models written in phase domain or in modal domain [1]. If the transmission line is represented by its modes, the line operations are effectuated in modal domain and after that transformed back to phase domain. This way a transmission line with n phases can be decoupled in its n exact modes and each mode can be represented as being a single-phase line transmission. In multiphase lines, transformation phase-mode-phase is done by a modal transformation matrix [2]. Because per unit length longitudinal impedance matrix and shunt admittance matrix are frequency dependence, modal transformation matrices are frequency dependence too. Therefore the modal transformation matrices are usually obtained by numerical methods that not permitting the development of an analytical model this line for. Thereby, if it is obtained explicitly a function that lists the elements of the transformation matrix with the line parameters, it is possible to develop a direct model in phase’s domain of a transmission line, depending only of its parameters. Advantages principal of a transmission line model de- veloped directly in phase domain are: the model devel- oped in phases domain, the currents and voltages can be obtained in any situation of analysis line (e.g. in analysis line considering the line in phase-ground and\or phase- phase short circuit), which cannot be easily done in mo- dal model; all terms present in equations that represent this model are functions only of [Z] and [Y] parameters, which will allow representing the phases in time domain. This paper proposes to show the development of a model for a non-transposed three-phase transmission line with a vertical symmetry plane in phase modal. 2. Alternative Model for Three-Phase Transmission lines A transmission lines with phases are characterized by it’s per unit length longitudinal impedance, matrix [Z], and shunt admittance, matrix [Y]. If this line is represented in modal domain, has the following relationship [2]: [][][][] t mI I TZT (1) -1 [ ][][][] t mI I YTYT (2) In (1) and (2), the matrices [Zm] and [Ym] are per unit length impedance and admittance modal matrices, respec- tively. Matrices [Zm] and [Ym] are diagonal matrices and [TI] is a transformation matrix whose columns are the eigenvectors associated with the eigenvalues of the product [Y][Z]. In (1) [TI]t is the transpose of [TI] and in (2) [TI]-t is the inverse of [TI]t. Copyright © 2013 SciRes. EPE  C. G. CARVALHO ET AL. 1491 In modal domain, a multiphase line with n phases is represented by their n propagation modes which behave as n decoupled single-phase lines. Figure 1 shows a generic mode of the multiphase transmission line. In Figure 1, EA e EB are, respectively, modal voltages at A and B terminals, respectively, while ImA and ImB are, respectively, modal currents at A and B terminals, written in modal domain. The relationship between phase and modal values are obtained as follows [3]: mB cosh() -Isinh() AB C EEd Zd (3) mB -I cosh()sinh( ) B mA C E dd Z (4) In (3) and (4), the terms γ and ZC are, respectively, modal propagation function and modal characteristic impedance [4, 5]. Considering a generic three-phase transmission line, this line will be represented in modal domain by its three propagation modes. Thus, applying (3) and (4) for each mode, have the following voltage and current vectors in modal domain: mB [][][]-[B][I] AB EAE (5) B [][C][E ][][] mA mB DI (6) In (5) e (6), the matrix [D] is equal to the matrix [A] and the matrices [A], [B] and [C] are written as: 1 2 3 cosh ()00 []0cosh()0 00cosh( m m m d Ad d ) ) (7) 11 22 33 sinh ()00 []0sinh()0 00sinh( Cm m Cm m Cm m Zd BZd d (8) 1 1 2 2 3 3 1sinh ()00 1 []0sinh( )0 1 00sinh( m Cm m Cm m Cm d Z Cd Z d Z ) (9) Figure 1. A generic mode multiphase transmission line. It is known that phase and mode values so satisfy the following relationships [3]: [][ ][] t I ETV (10) 1 [][][] mI TI (11) In (10), the vectors [V] and [E], are transversal voltages written in phase and modal domain, respectively, an l cu (5) and (6), and making the appropriate mathematical manipul d in (11), the vectors [I] and [Im], are the longitudina rrents written in phase and modal domain, respectively. Replacing (10) and (11) in ations, are obtained: 1 IB [ ][][][][ ][][][][] tt t AI IBI VTATVTBTI (12) 1 [][][][][ ][][][][] t AI IBIIB TCTVTDTI (13) Equations (12) and (13) show the relationships between phase values at A and B terminals of a generic three- phase line. The vectors [VA] and [VB] contain the phase vo s, respectively. Matrices [TI], [A], [B], [C] and [ obtained according to three-phase line parameters. Equations (12) and (13) represent an equat th ltages in A and B terminals, respectively, while [IA] and [IB] contain the phase currents in A and B terminal D] are ion model at possibility to obtain the phase values for a generic three-phase transmission line. However, the development of this model is only possible if the matrix [TI] is obtained analytically. It is known that [TI] columns are eigenvectors associated to the product [Y][Z] [2]. Therefore, it is possible to obtain explicitly a function that represents the elements of each column of the matrix [TI] according to the three-phase line parameters. In this case, to get the elements of the matrix [TI] is necessary, first, calculate the eigenvalues corresponding to the product [Y][Z] through [2]. However, for a generic three-phase transmission line, the obtaining these eigenvalues depends on the polynomial solution of degree 3, which is not easily found. A solution in this case is to consider a non-transposed three-phase transmission line with a vertical symmetry plane. This line can be represented by a system consisting of a single-phase and two-phase line [6]. Then the three-phase line is separated in its propagation modes by using two modal transformation matrices: the first is the Clarke’s matrix [7]; the second is an adequate modal transformation matrix whose elements are frequency dependences [2, 6]. This way, to represent a three-phase line directly in phase domain, using (12) and (13), it is need to obtain, analytically, the polynomial solution of degree 2. There- fore, as well as in single-phase line, the currents and vol- tages of a three-phase line are obtained directly in the phase domain. Figure 2 shows a non-transposed three-phase trans- Copyright © 2013 SciRes. EPE  C. G. CARVALHO ET AL. 1492 mission line with a vertical symmetry plane. For this line, the longitudinal impedance [Z] and tran- sverse admittance [Y] are written as [7]: 11 12 12 12 22 23 12 23 22 [] zzz zzz zzz (14) yyy 11 1212 12 22 23 12 23 22 []Yyyy yyy (15) The line in Figure 2 can be represented as a system consisting by a single-phase line and two-phase line. In this representation, the three-phase line can be decoupled into exact modes by using two tra [6]. Initially, Clarke’s matrix is used line in their quasi-modes α and 0 and its exact mode β and, after that, an adequate modal tran decouples the quasi-modes α and 0 Figure 3 shows a schematic representation of the modal de (17) nsformation matrices for decoupling the sformation matrix into exact mode. composition process by using two transformation matrices. If in (1) and (2) the transformation matrix [TI] is substituted by Clarke’s matrix, the impedance and admittance, in this case, are written, respectively, as being: 0 [][][][] t clarke clarke ZTZT (16) -1 0 [][][][] t clarke clarke YTYT Considering the line parameters, equations (14) and (15), the matrices [Zαβ0] and [Yαβ0], are rewritten, respec- tively, as [6,7]: 1112 22 231112 22 23 02223 12 (24) 0() 33 [] 00 zzzz zzzz Zzz (18) 11 12 22 231112 21 2 ()0(4) 333 zzzzz z 22 23 ()zz Figure 2. Non-transposed three-phase transmission line with a vertical symmetry plane. Figure 3. Modal representation by using two transfor- mation matrices. 1112 22 231112 22 23 02223 1112 22 23111222 23 12 (24) 0() 33 [] 00 21 ()0(4)( 33 yyyy yyyy Yyy yyyyy yyy 2 ) 3 (19) In (16) and (17), it is verified that the line shown in Figure 2 can be represented as a single-phase and a two t is excluded in (18) and (19), are ob- tained the longitudinal impedance [Zα0] and transversal admittance [Yα0] are given by: - phase line and there is not coupling between them [6]. If β componen 1112222311 122223 0 111222 23111222 23 33 3 12 (2 4)() 33 [] 212 ()(4)( zzzz zzzz Z zzzzz zz )z (20) 1112 222311122223 0 1112 22 23 12 (2 4)() 33 [] 212 () 33 yyyy yyyy Y yy yy 111222 23 (4)() 3 y yyy (21) These matrices represent a two-phase line without a vertical symmetry plane [6]. In (20), impedance matrix elements are written as: 1112 22 23 1(2 4) 3 zzzz (22) 0 11122223 2() 3 zzzz (23) 011122223 (4 )( ) 33 12 zz zz (24) In (21), admittance matrix elements [Yα0] are written as: 1112 22 23 1(2 4) 3 Yyyyy (25) 0111222 2() 3 Yyyy 23 y (26) 01112222 12 (4)(3 Yy y yy itudinal and shunt three-phase line parameters. In Figure 3, a modal decomposition of t line is done by using modal transformation mα0 which diagonalizes the [Yα0][Zα0] [2]. Immediately, it can be obtained a relationship between the elem column of [Tα0] and the three-phase line parameters. In this case, eigenvalues are obtained by the solution of a polynomial of degree 2, whose roots are written as: ) (27) 33 In (22)-(27) all elements are written only according to long he two-phase atrix [T], ents of each Copyright © 2013 SciRes. EPE  C. G. CARVALHO ET AL. Copyright © 2013 SciRes. EPE 1493 writing in terms these parameters. 22 1122112211221221 )S (28) 1 ()2 4 2 SSS SSSS Obtained [Tα0] can be established an explicit relationship between two-phase line values and three-phase line parameters. Thereby, are obtained the currents and volt- age phases of the two-phase line written according to only three-phase line parameters (Figure 2). 22 11221122112212 21 2 ()24)SSS SSSSS 2 In (28) and (29), S11, S12, S21 and S22 are the elements of the matrix [S] obtained by calculating the product [Yα0][Zα0]: (29) 00000 0000000 [] YZYZYZY S YZYZYZY (30) Therefore, [Tα0] can be written as: 12 12 2 2 11 11211212 011 1112 2 22 11 11211212 ()( ) [] ()( ) SS SSSS TSS SSSS 2 2 2 tically according to three-phase line parameters since the elements of the matrix [S] are fB Verifies in Figure 3 that β component is an exact mode of three-phase line. Thus, the currents and voltages in this mode are obtained from the equations (3) and (4). Obtained the values in α, β and 0 components, the next step is the conversion of these values to domain phases. Process result is a series of equations that allows to ob- tain currents and voltages phase of the three-phase line. These equations represent a direct model developed in phase domain of three-phase line in Figure 2. Considering the matrix [Tα0] obtained in (31), the equations (12) and (13) are rewritten as: (31) 12 [][][][ ][] AB VNVNI (32) Considering the expression (31), can be say that [Tα0] is writing analy34 [][][][][] AfBB NI NV (33) where: 1 1 222 1 []2( ) da db db Ncacbcb da bc 1 1 cosh ()00 0 cosh( ) 0 00cosh() cosh ()00 00 0 1 0110cosh() 2011 00cos 222 1 m m m dd ca cb cbd dd cb db db 2 2 2 cosh ()00 o()0 0cosh() m m m ddd 0 h()d 2( )ca da da da bcca da da 0c sh 0 (34) 11 211 11 () 222 1Cm m Zsenh d de dfdf 0 0 [] 0()0 2( )00 () () 00 00 0 1 011 0()0 2011 00 ( 2 1 2( ) Cm m Cm m C C C Nc ecfcf Zsenhd da bccecfcfZsenhd Zsenh d Zsenh d Zsenh d dabc 22 22 22 () 00 22 0()0 00 () Cm m Cm m Cm m Zsenhd gb hb hb ga hahaZsenhd ga haha ) senh d (35) 1 3 1 1 cosh ()00 222 1 []0 cosh()0 2( )00cosh() cosh ()00 00 0 1 0110cosh()0 201100cosh() 222 1 2( ) m m m d he hfhf Ngegfgfd he gfge gfgfd ddd gf hfhf ge hehe he gfg 2 2 2 cosh ()00 0cosh()0 00cosh( m m m dd ehehe d ) (36)  C. G. CARVALHO ET AL. 1494 1 1 4 1 1 1 1 1() 00 222 11 [] 0()0 2( ) 1 00 () 1() 00 000 11 011 0()0 2011 1 00 () m Cm m Cm m Cm C C C senh d Z ha hbhb Ngagbgb senhd he gfZ ga gb gb senh d Z senhd Z senhd Z senh d Z 2 2 2 2 2 2 1() 00 222 11 0()0 2( ) 1()00 m Cm m Cm m Cm senh d Z cf df df ce de desenhd he gfZ ce de de enh d Z (37) In (34)-(37), the terms γm1 and γm2 are, respectively, propagation functions in modes 1 and 2 of the two-phase line, while ZCm1 and ZCm2 are, respectively, the characteristic impedances in modes 1 and 2 this line. Also, in (34)-(37), γβ and ZCβ are, respectively, propagation function and characteristic impedance in β. All these elements are calculated according to three-phase line parameters. In (34)-(37) a, b, c and d elements are written as: 11 21 2 63 TT a (38) 21 11 36 TT b (39) 12 22 2 63 TT c (40) 22 12 36 TT d (41) In (38)-(41), T11, T12, T21 and T22 are [Tα0] elements obtained in (31). In (34)-(37) e, f, g and h elements are written as: 11 21 2 63 X e (42) 21 11 36 X f (43) 12 22 2 63 X g (44) 22 12 36 X h In (42)-(45), X11, X12, X21 and X22 are [Tα0]t elements obtained by the inverse transpose of [Tα0]. It is observed in equations (32) and (33) that three- phase line model obtained directly in phase domain is calculated according to [N1], [N2], [N3] and [N4] which are obtained only according to longitudinal and shunt parameters of the three-phase line, show in Figure 2. Therefore, equations (32) and (33) represent an analytical model for three-phase lines developed directly in the phase domain. 3. Results Results obtained with the model deve phase domain will be compared to results obtained using a model developed modes domain [2]. The curves will be analyzed for the 200 km transmission line in the interval 10-2 Hz 105 Hz. To analyze the behavior of current curves were used the parameters of a 440 kV three-phase line transmission line [6] (Figure 4). Classical modal method used in simulations of the line is Newton-Raphson method [2]. The line was energized by a constant tension source in two situations, the open and short circuit line [8]. (45) loped directly in Figure 4. 440 kV three-phase line transmission line. Copyright © 2013 SciRes. EPE 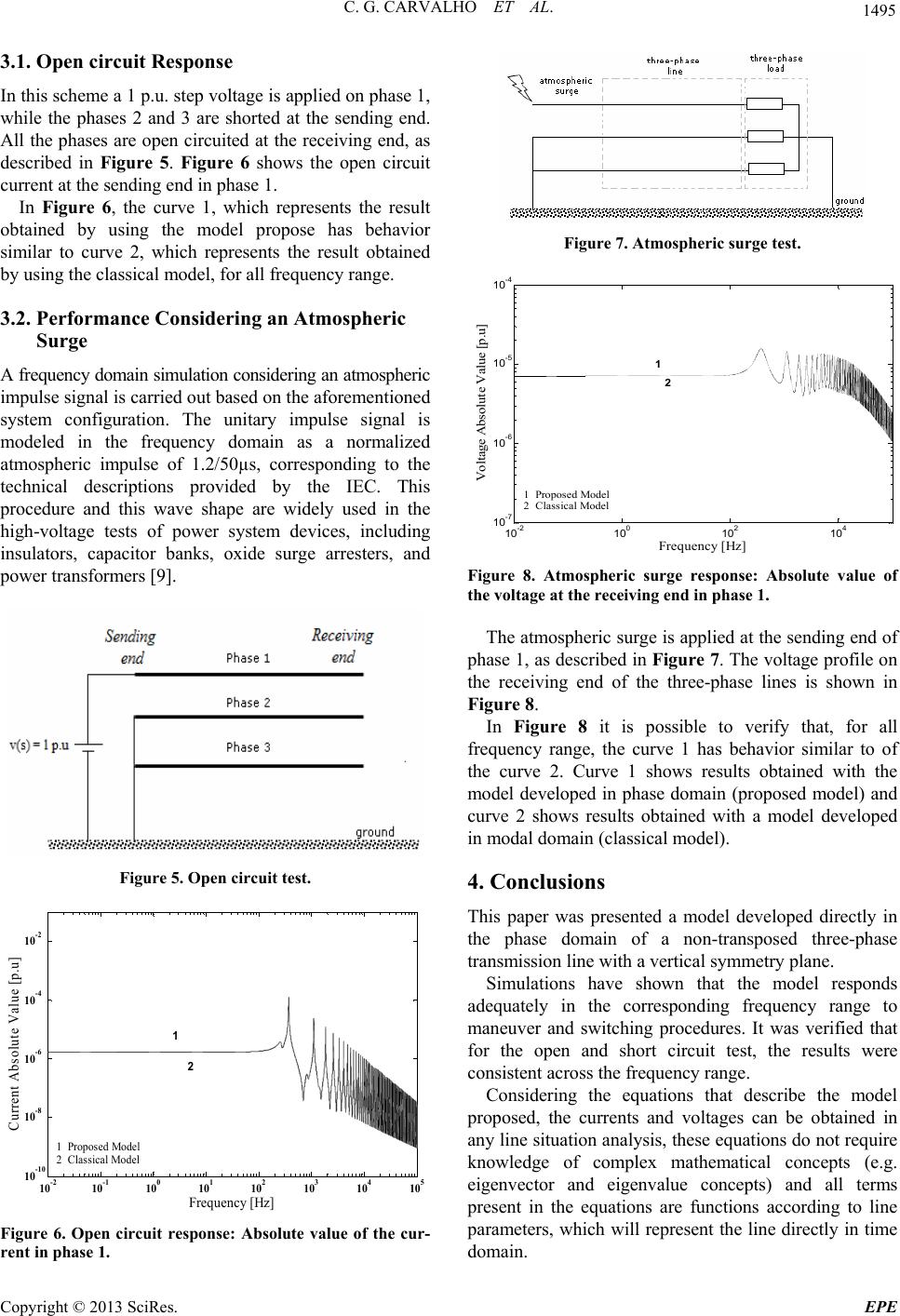 C. G. CARVALHO ET AL. 1495 3.1. Open circuit Response In this scheme a 1 p.u. step voltage is while the phases 2 and 3 are shorted at the sending end. All the phases are open circuited described in Figure 5. Figure 6 shows the open circuit current at the sending end in phase 1. In Figure 6, the curve 1, whic obtained by using the model propose has behavior similar to curve 2, which repr by using the classical model, fo zed at this wave shape are widely used in the high-voltage tests of power system devices, including pacitor banks, oxide surge arresters, and applied on phase 1, at the receiving end, as h represents the result esents the result obtained r all frequency range. 3.2. Performance Considering an Atmospheric Surge A frequency domain simulation considering an atmospheric impulse signal is carried out based on the aforementioned system configuration. The unitary impulse signal is modeled in the frequency domain as a normali mospheric impulse of 1.2/50µs, corresponding to the technical descriptions provided by the IEC. This procedure and insulators, ca power transformers [9]. Figure 5. Open circuit test. 10 -2 10 -1 10 0 10 1 10 2 10 3 10 4 10 5 10 -10 10 -8 10 -6 10 -4 10 -2 Frequency [Hz] 1 Proposed Model 2 Classical Model Figure 6. Open circuit response: Absolu rent in phase 1. Cu rre Figure 7. Atmospheric surge test. 10 -2 10 0 10 2 10 4 10 -7 10 -6 10 -5 10 -4 nt Absolute Value [p.u] 1 2 te value of the cur- Frequency [Hz] Vo 1 Proposed Model 2 Classical Model Figure 8. Atmospheric surge response: Absolute value of the voltage at the receiving end in phase 1. The atmospheric surge is applied at the sending end of phase 1, as described in Figure 7. The voltage profile on the receiving end of the three-phase lines is shown in Figure 8. In Figure 8 that, for all equency range, the curve 1 has behavior similar to of the curve 2. Curve 1 shows results obtained with the model developed in phase domain (proposed model) and curve 2 shows results obtained with a model developed in modal domain (classical model). 4. Conclusions This paper was presented a model developed directly in the phase domain of a non-transposed three-phase transmission line with a vertical symmetry plane. Simulations have shown that the model responds adequately in the corresponding frequency range to maneuver and switching procedures. It was verified that for the open and short circuit test, the results wer urrents and voltages can be obtained in any line situation analysis, these equations do not require knowledge of complex mathematical concepts (e.g. eigenvector and eigenvalue concepts) and all terms present in the equations are functions according to line parameters, which will represent the line directly in time domain. ltage Absolute Value [p.u] 1 2 it is possible to verify fr e consistent across the frequency range. Considering the equations that describe the model proposed, the c Copyright © 2013 SciRes. EPE  C. G. CARVALHO ET AL. Copyright © 2013 SciRes. EPE 1496 Therefore, the developed model can be used as an alternative model in the analysis of transient phenomenons that occur in transmission lines of electric power system. 5. Acknowledgements The authors thank LETEL group – Electromagnetic Transient Laboratory – throughout complicity collaboration andlvim ientífico e REFERENCES [1] A. B. Fernandes and W. L. A. Neves, “Phase-domain Transmission Line Models Considering Frequency De- pendent Transformation Matrices,” IEEE Transactions on Power Delivery, Vol. 19, No. 2, 2004, pp. 708-714. doi:10.1109/TPWRD.2003.822536 and ento Conselho Nacional de Desenvo Tecnológico (CNPQ). C [2] L. M. Wedephol, H. V. Nguyen and G. D. Irwin, “Fre- quency-Dependent Transformation Matrices for Un- transposed Transmission Lines Using Newton-Raphson Method,” IEEE Transactions on Power Systems, Vol. 11, No. 3, 1996, pp. 1538-1546. doi:10.1109/59.535695 [3] A. Budner, “Introduction of Frequency-Dependent Line Parameters into an Electromagnetic Transients Program,” IEEE Transactions on Power Apparatus and Systems, Vol. 89, No. 1, 1970, pp. 88-97. doi:10.1109/TPAS.1970.292674 [4] L. Marti, “Low-order Approximation of Transmission line Parameters for Frequency Dependent Models,” IEEE Trans. Power App. and Systems, Vol. PAS-102, No. 11, 1983, pp. 3582 - 3589. doi:10.1109/TPAS.1983.317705 [5] Chipman and A. Robert, “Teoria e Problemas de Linhas de Transmissão,” Ed. McGraw-Hill from Brazil, São , A. J. Prado and J. Pissolato, Paulo, 1972. [6] S. Kurokawa, R. S. Daltin “An Alternative Modal Representation of a Symmetrical Non-transposed Three-Phase Transmission Line,” IEEE Transactions on Power Systems, Vol. 22, No. 1, 2007, pp. 500-501. doi:10.1109/TPWRS.2006.889117 [7] M. C. Tavares, J. Pissolato and C. M. Portela, “Mode Domain Multipne Model – Use in Transient Stud Power Delivery, hase Transmission Li ies,” IEEE Transaction on Vol. 14, No. 4, 1999, pp. 1533-1544. doi:10.1109/61.796251 [8] B. Gustavsen and A. Senlyen, “Combined Phase and Modal Domain Calculation of Transmission Transients Based on Vector Fitting,” IEEE Transactions on Power Delivery, Vol. 13, No. 2, 1998. doi:10.1109/61.660936 [9] IEC 60060–1: ‘High-voltage Test Techniques – part 1: General Definitions and Test Requirements,” Ed. 3, 2010.
|