Energy and Power Engineering, 2013, 5, 1468-1473
doi:10.4236/epe.2013.54B278 Published Online July 2013 (http://www.scirp.org/journal/epe)
DC-Link Based Micro-grid System
Miro Milanovič, Mitja Truntič, Miran Rodič
University of Maribor; FERI, SI-2000 Maribor, Slovenia
Received April, 2013
ABSTRACT
Design and evaluation of dynamic model of multi-input/multi-output power converter consisting of six converters con-
nected by dc-link will be presented in the paper. The model was created in Matlab/Simulink based on the existing sys-
tem, with the goal of evaluating various power management strategies, where only transient behavior in case of changed
operating regime is of interest. In future the model will be used as a Software-In-the-Loop development tool for the
design of supervisory control algorithms.
Keywords: Power Management; Power Electronics; Simulation; Modeling; Control
1. Introduction
In many applications there is a requirement for multiple
power sources to be connected together, providing the
power for a single or multiple loads. For example in
electric and hybrid vehicles, distributed generation sys-
tems etc., multiple sources of electric energy are avail-
able, which have to be connected together in order to
maximize the efficiency of the overall system under the
different operating conditions.
This kind of operation has recently achieved a wide
attention due to the extensive use in the electric and hy-
brid vehicles [1,2], as well as in the distributed [3,4] and
micro-generation systems [5,6]. Especially the use in
alternative and renewable sources utilization can be
counted among the most interesting applications [4,6],
[7]. Due to the nature of this kind of systems, the super-
visory control is required, especially for the performance
of power and energy management [8-10]. However, the
converters of that complexity become relatively hard to
manage, and in the early stage of development, a lot of
attention has to be given to the safety of the operation,
which has to be set to a much higher level than the one
required in the normal operation. Thus the possibilities of
testing new algorithms are limited and information ob-
tained is in many cases not sufficient. In development of
modern industrial applications simulations are an effi-
cient tool, but applied simulation models have to be pre-
cise enough to ensure reliable results and at the same
time not too complex in order to allow them to be per-
formed in a reasonable time on the available computers,
which in our case are PCs.
In the presented case a multi-input/multi-output power
converter was modeled and simulated. The paper will be
organized in the way, which will allow the insight into
the bottom-up development of the model. After short
introduction a complete system will be presented briefly,
to give a basic idea of the model requirements. This will
be followed by the presentation of the applied converters
and their models. In the next step interconnection of the
converters will be presented and explained. Next stage
will be the presentation of the supervisory control. This
is the main purpose of the model, thus it will be pre-
sented in more details. Example of a simple supervisory
control will be described together with its presentation by
the means of state automata in Matlab/Simulink State-
flow tool and then the results will be presented, first ex-
perimental and afterwards numerical (simulation) ones.
Finally, the conclusion will summarize the paper and
give some ideas for the future work.
2. System Model
Multi-input/multi-output converter consists of six con-
verter units (C1-C6), which are connected into the sys-
tem using the DC link (Figure 1). Three bi-directional
(C2, C3 and C4) and three unidirectional (C1, C5 and C6)
converter units (in the terms of energy exchange) are
used. For the short-term transfer operation system is
supported by the capacitor banks applied at the DC-link
sides of all converters. The modularity of the system was
an important issue due to the demands set, where special
attention was on the maintenance. Possibility to ex-
change both power and controller hardware units was
required. As it can be seen from converter schemes in
Figures 2 (a)-(f), there are the equal half-bridge units
used as basic power electronics blocks. Based on this
requirement the power (Figure 3(a)) and microcontroller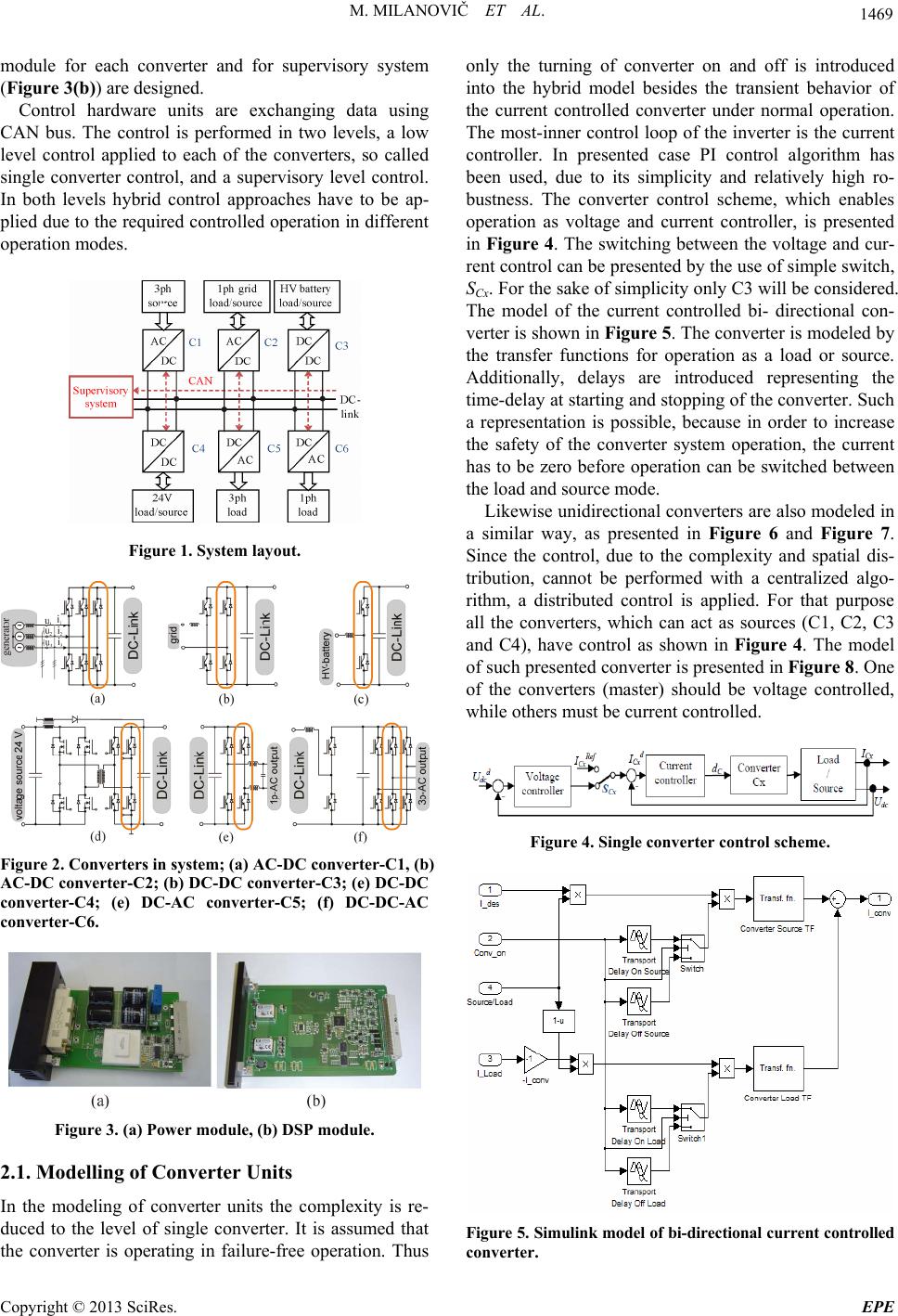

M. MILANOVIČ ET AL. 1469
module for each converter and for supervisory system
(Figure 3(b)) are designed.
Control hardware units are exchanging data using
CAN bus. The control is performed in two levels, a low
level control applied to each of the converters, so called
single converter control, and a supervisory level control.
In both levels hybrid control approaches have to be ap-
plied due to the required controlled operation in different
operation modes.
Figure 1. System layout.
Figure 2. Converters in system; (a) AC-DC converter-C1, (b)
AC-DC converter-C2; (b) DC-DC converter-C3; (e) DC-DC
converter-C4; (e) DC-AC converter-C5; (f) DC-DC-AC
converter-C6.
Figure 3. (a) Power module, (b) DSP module.
2.1. Modelling of Converter Units
In the modeling of converter units the complexity is re-
duced to the level of single converter. It is assumed that
the converter is operating in failure-free operation. Thus
only the turning of converter on and off is introduced
into the hybrid model besides the transient behavior of
the current controlled converter under normal operation.
The most-inner control loop of the inverter is the current
controller. In presented case PI control algorithm has
been used, due to its simplicity and relatively high ro-
bustness. The converter control scheme, which enables
operation as voltage and current controller, is presented
in Figure 4. The switching between the voltage and cur-
rent control can be presented by the use of simple switch,
SCx. For the sake of simplicity only C3 will be considered.
The model of the current controlled bi- directional con-
verter is shown in Figure 5. The converter is modeled by
the transfer functions for operation as a load or source.
Additionally, delays are introduced representing the
time-delay at starting and stopping of the converter. Such
a representation is possible, because in order to increase
the safety of the converter system operation, the current
has to be zero before operation can be switched between
the load and source mode.
Likewise unidirectional converters are also modeled in
a similar way, as presented in Figure 6 and Figure 7.
Since the control, due to the complexity and spatial dis-
tribution, cannot be performed with a centralized algo-
rithm, a distributed control is applied. For that purpose
all the converters, which can act as sources (C1, C2, C3
and C4), have control as shown in Figure 4. The model
of such presented converter is presented in Figure 8. One
of the converters (master) should be voltage controlled,
while others must be current controlled.
Figure 4. Single converter control scheme.
Figure 5. Simulink model of bi-directional current controlled
converter.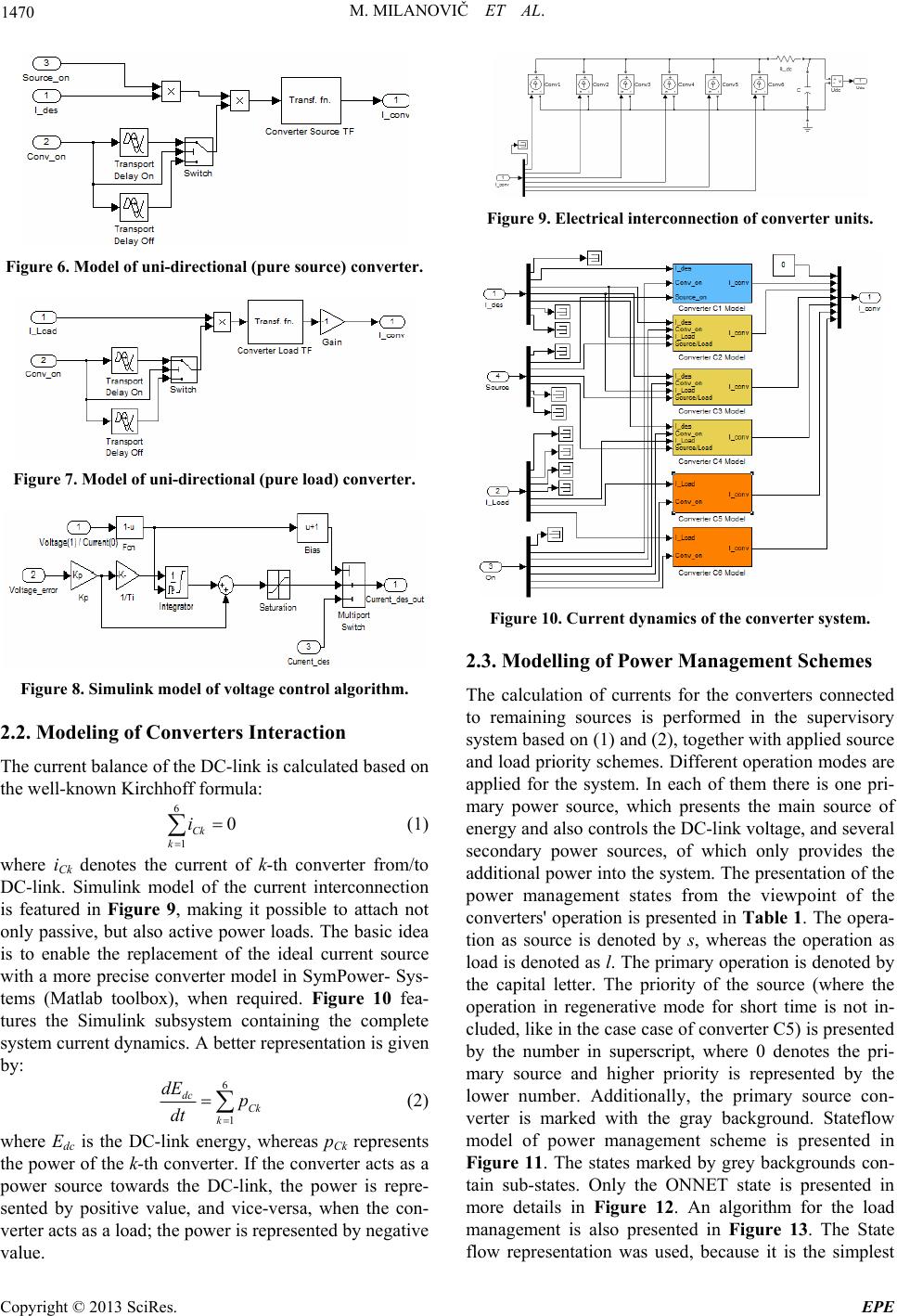

M. MILANOVIČ ET AL.
1470
Figure 6. Model of uni-directional (pure source) converter.
Figure 7. Model of uni-directional (pure load) converter.
Figure 8. Simulink model of voltage control algorithm.
2.2. Modeling of Converters Interaction
The current balance of the DC-link is calculated based on
the well-known Kirchhoff formula:
6
1
0
Ck
k
i


 (1)
where iCk denotes the current of k-th converter from/to
DC-link. Simulink model of the current interconnection
is featured in Figure 9, making it possible to attach not
only passive, but also active power loads. The basic idea
is to enable the replacement of the ideal current source
with a more precise converter model in SymPower- Sys-
tems (Matlab toolbox), when required. Figure 10 fea-
tures the Simulink subsystem containing the complete
system current dynamics. A better representation is given
by:
6
1
dc Ck
k
dE p
dt 
 (2)
where Edc is the DC-link energy, whereas pCk represents
the power of the k-th converter. If the converter acts as a
power source towards the DC-link, the power is repre-
sented by positive value, and vice-versa, when the con-
verter acts as a load; the power is represented by negative
value.
Figure 9. Electrical interconnection of converter units.
Figure 10. Current dynamics of the converter system.
2.3. Modelling of Power Management Schemes
The calculation of currents for the converters connected
to remaining sources is performed in the supervisory
system based on (1) and (2), together with applied source
and load priority schemes. Different operation modes are
applied for the system. In each of them there is one pri-
mary power source, which presents the main source of
energy and also controls the DC-link voltage, and several
secondary power sources, of which only provides the
additional power into the system. The presentation of the
power management states from the viewpoint of the
converters' operation is presented in Table 1. The opera-
tion as source is denoted by s, whereas the operation as
load is denoted as l. The primary operation is denoted by
the capital letter. The priority of the source (where the
operation in regenerative mode for short time is not in-
cluded, like in the case case of converter C5) is presented
by the number in superscript, where 0 denotes the pri-
mary source and higher priority is represented by the
lower number. Additionally, the primary source con-
verter is marked with the gray background. Stateflow
model of power management scheme is presented in
Figure 11. The states marked by grey backgrounds con-
tain sub-states. Only the ONNET state is presented in
more details in Figure 12. An algorithm for the load
management is also presented in Figure 13. The State
flow representation was used, because it is the simplest

M. MILANOVIČ ET AL. 1471
Table 1. Power Management States – Converter Roles.
Converter
State Primary
source C1 C2C3 C4 C5C6
INIT None Off Off Off Off Off Off
STANDBY None Off OffOff Off Off Off
ONNET Grid Off
S0/l s1/L L s/LL
NETSUPP Generator S0 s/L S1/l S2/l s/LL
BAT24V 24V battery Off Offs1/L S0/l s/LL
BATTERY HV battery Off OffS0/l L s/LL
ISLAND Generator S0 Off S1/l L s/LL
FAULT None Off Off Off Off Off Off
NETSUPP
ONNET
STANDBY
during: On=ml('[0,0,0,0,0,0,0]');
during: Source=ml('[0,0,0,0,0,0,0] ');
during: Voltage_control=ml('[0,0,0,0,0,0,0]');
entry:P_c=ml('[0,0,0,0,0,0,0]');
entry:B_c=1;
BAT24V
ISLAND
BATTERY
entry: On=ml('[0,0,0,1,1,1,1] ');
entry: Source_avail=ml('[0,0,0,1,0,0,0] ');
entry: Source=ml(' [0,0,0,1,0,0,0 ]');
entry: Voltage_control=ml('[0, 0,0,1,0,0,0]');
during:B_c=1;
[Mode==1]
[Mode==5]
[Mode==1]
3
[Mode==1]
[Mode==5]
[Mode==5]
5
[(Mode!=1)&&(BatS>0)]
[Mode==1]
2
[Mode==5]
[Mode==5]
[Mode==4]
[Mode==4]
[(Mode==3)||(Mode==2)||(Mode==4)]
[Mode==0]
[(Mode==0)||((Mode!=1)&&(BatS==0))]
[Mode==2]
3
[Mode==0]
[Mode==0]
1
[Mode==0]
[(Mode==3)&&(BatS>0)]
1
[Mode==4]
4
[Mode==2]
2
[(Mode==3)&&(BatS> 0)]
[(Mode==4)||(Mode==5)]
4
[(Mode==3)&&(BatS>0)]
Figure 11. Stateflow representation of the power manage-
ment model.
ONNET
ent r y: O n=m l ( ' [0, 0, 1, 1, 1, 1,1] ') ;
ent r y: Sou r ce= ml('[ 0,0,1,0,0,0, 0] ') ;
ent r y: Sou r ce_avail= ml ( '[ 0, 0, 1,1, 0, 0, 0] ');
ent r y: Vol t age_con t r ol= m l ( '[ 0, 0, 1, 0,0, 0, 0] ') ;
ONNET_ HVB
entry: Source[3]=1;
during:P_c[3]=P_df-0.8 *P_a[ 2];
during:B_c=1;
ONNET_ BC
entry: Source[3]=0;
during:P_c[3]=P_a[3];
during:B_c=0;
ONNET_S
entry: Source[3]=0;
during:P_c[3]=0;
during:B_c=1;
[Mode==1]
[Mode==5]
3
[Mode==1]
[Mode==1]
[((P_d > (P_a[2]))&&(BatS>1))|| ((Mode!=1)&&(BatS==0))]
2
[Mode==5]
1
[(Mode!=1)&&(BatS>0)]
2
[(( P_d < (0. 8*P_a[2] ) )&&(M ode==1) ) ||( Mode!=1)]
1
[(BatS >2)||(Mode!=1) ]
[(BatS<2)&&(Mode==1)]
3
[(Mode==3)||(Mode==2)||(Mode==4)]
4
[Mode==1]
Figure 12. Stateflow representation of the ONNET opera-
tion mode.
all_on
during:Load_On= ml('[0,1,1,1,1,1,1]');
exit: mode_x=mode;
first_off
during:Load_On[priority[ 3]]=0;
exit: mode_x=mode;
second_off
during:Load_On[priority[ 2]]=0;
third_off
during:Load_On[priority[ 1]]=0;
fourth_off
during:Load_On[priority[ 0]]=0;
[mo de_x!=mode]
[mode_x!=mode]
2
[mod e_x!=mode]
1
[mode _x!=mode]
2
[(I_conv[priority [3]]+I_conv[priority[2]]+I_conv[priority[1]]+I_conv[priority[0]])>P_avai l_max]
[(I_conv[priority [2]]+I_conv[priority[1]]+I_conv[priority[0]])>P_avai l_max]
1
[(I_conv[priority[1]]+I_conv[priority[0]])>P_ avai l_max]
2
[(I_conv[priority[0]])>P_av ail_max]
1
Figure 13. Algorithm for the load management.
way to present such kind of algorithms. Stateflow up-
grades the state automata representation of the system by
mathematical and logical features, together with the pos-
sibility of including events. Furthermore, by designing
algorithms in Stateflow it is not only possible to use the
Matlab inherent automatic code generation (giving C
code as a result), but also to enforce systematic approach
on the designer. In Matlab/Simulink it is possible to ex-
change the Stateflow block with a s-function block,
making it possible to evaluate the algorithms written di-
rectly in C-code, which is an important goal for the fu-
ture use of the converter system model.
3. Experimental and Simulation Results
3.1. Laboratory Set-up
Experiments were performed on the custom design hard-
ware, with the master and converter control units using
TI TMS320F2809 microcontroller. The algorithms for
voltage and current control were executed in 25µs time
interval, whereas power management algorithm was ex-
ecuted in 10 ms time interval. The multi-converter sys-
tem is shown Figure 14. Each power module contains an
IGBT converter leg, like the one presented in Figure
3(a). The power modules are fully interchangeable, and
thus oversized for the majority of converters. This makes
the system more useful for the experimenting purposes.
3.2. Simulation Results
Unlike most of the technical papers, simulation results
follow the experimental ones. This is due to the fact, that
the model and its operation are a result in the presented
case. The model, containing all sub-systems described
above is presented in Figure 17. The model additionally
includes battery status model to serve as output for test-
ing operation in case of various battery states (low,
full, …). Simulation results in Figure 18 present a run-
trough over all the active operating states (presented in
Table 1), where states are represented by the value of the
variable mode (0 – system turned off, 1–ONNET,
Figure 14. Functional prototype of the system.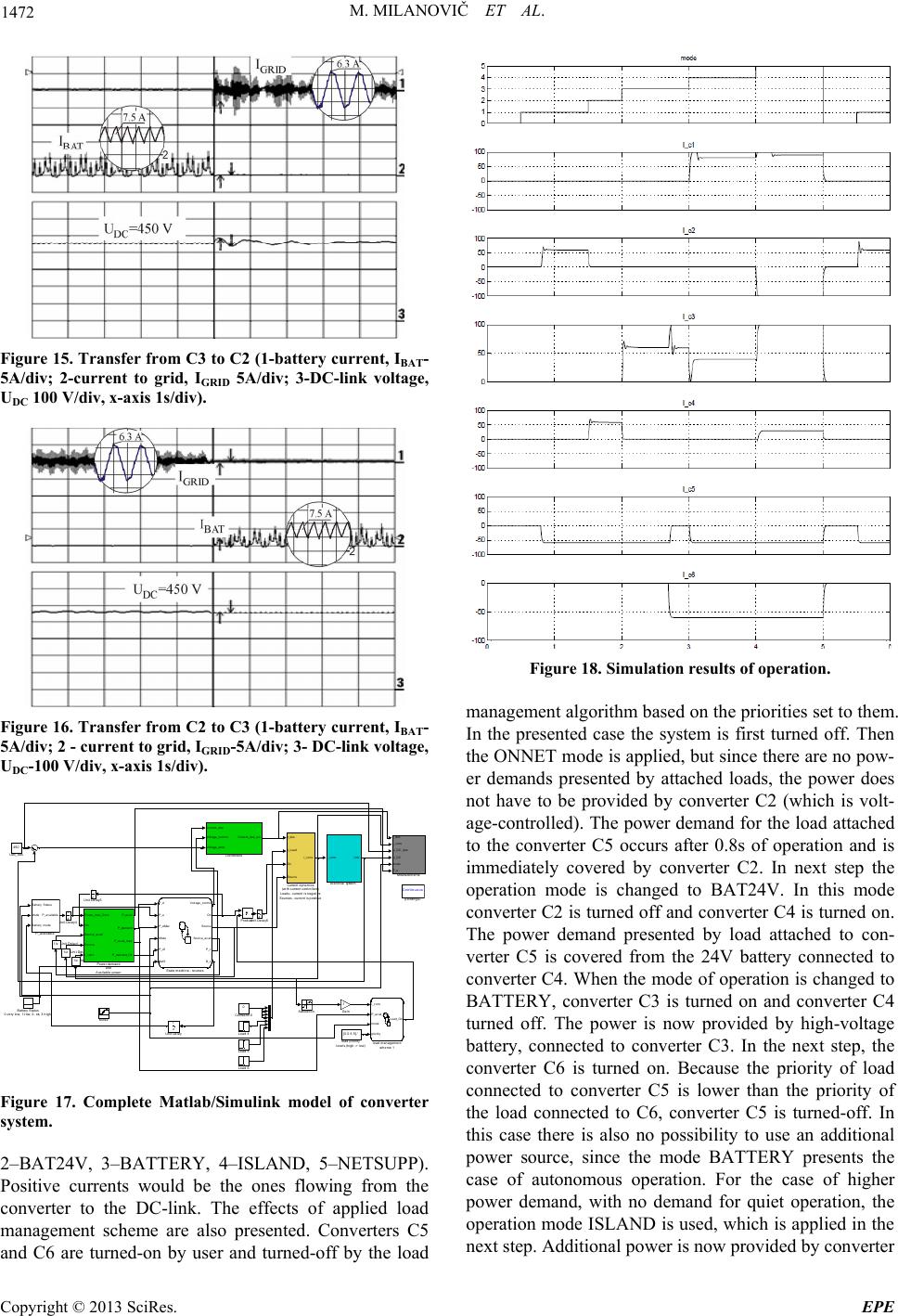

M. MILANOVIČ ET AL.
1472
Figure 15. Transfer from C3 to C2 (1-battery current, IBAT-
5A/div; 2-current to grid, IGRID 5A/div; 3-DC-link voltage,
UDC 100 V/div, x-axis 1s/div).
Figure 16. Transfer from C2 to C3 (1-battery current, IBAT-
5A/div; 2 - current to grid, IGRID-5A/div; 3- DC-link voltage,
UDC-100 V/div, x-axis 1s/div).
Continuous
powergui
[0 0 6 5].'
load priority
levels (high -> low)
I_conv
P_avail_max
mode
priority
Load_On
load management
scheme 1
z
1
Unit Delay6
z
1
Uni t Del a y5
z
1
Uni t Del a y4
1/z Unit Delay3
1/z Unit Del ay2
1/z Unit Delay1
z
1
Unit Delay
450
Udc_des
P_d
P_a
P_aMax
Mode
P_df
BatS
Voltage_control
On
Source
Source_avail
P_c
B_c
State machine - sources
Saturation
Product
Power_max_Conv
On
Source_avail
Source
I_conv
P_avail
P_demand
P_avail_max
P_demand_filt
Power demand
and
Available power
Battery Status
Mode
Battery mode
P_available
P_available
Mode
I_des
I_conv
U_DC_des
U_DC
mode
P_a
Measurements
Load 6
Load 5
Load 4
-1
Gain
I_conv Udc
Electrical system
I_des
I_Load
On
Source
I_conv
Current dynamics
(with current cont rol lers)
Loads - current is negative
Sources - current is positive
Current_des
Voltage_control
Voltage_error
Current_des_out
Controllers
0
Constant10
Battery Status
0-very low, 1-low, 2- ok, 3-high
Figure 17. Complete Matlab/Simulink model of converter
system.
2–BAT24V, 3–BATTERY, 4–ISLAND, 5–NETSUPP).
Positive currents would be the ones flowing from the
converter to the DC-link. The effects of applied load
management scheme are also presented. Converters C5
and C6 are turned-on by user and turned-off by the load
Figure 18. Simulation results of operation.
management algorithm based on the priorities set to them.
In the presented case the system is first turned off. Then
the ONNET mode is applied, but since there are no pow-
er demands presented by attached loads, the power does
not have to be provided by converter C2 (which is volt-
age-controlled). The power demand for the load attached
to the converter C5 occurs after 0.8s of operation and is
immediately covered by converter C2. In next step the
operation mode is changed to BAT24V. In this mode
converter C2 is turned off and converter C4 is turned on.
The power demand presented by load attached to con-
verter C5 is covered from the 24V battery connected to
converter C4. When the mode of operation is changed to
BATTERY, converter C3 is turned on and converter C4
turned off. The power is now provided by high-voltage
battery, connected to converter C3. In the next step, the
converter C6 is turned on. Because the priority of load
connected to converter C5 is lower than the priority of
the load connected to C6, converter C5 is turned-off. In
this case there is also no possibility to use an additional
power source, since the mode BATTERY presents the
case of autonomous operation. For the case of higher
power demand, with no demand for quiet operation, the
operation mode ISLAND is used, which is applied in the
next step. Additional power is now provided by converter

M. MILANOVIČ ET AL.
1473
C1 and the converter C5 is consequently turned-on again.
In order to achieve the slower high-voltage battery dis-
charge, most of the power is provided by converter C1
and only a small portion by converter C3. Finally, the
last one of modes, NETSUPP, is applied. In this opera-
tion it is expected that converter C2 is supporting the
power grid by the maximal possible power (this is pre-
sented by the negative current for this controller), which
is, together with the power required by loads connected
to converters C5 and C6 provided not only by the gen-
erator (converter C1), but also by the C3 and in smaller
portion by C4. At the end of test the system is turned-off
and converters C5 and C6 are also turned-off.
To demonstrate the possibility of restarting at the end
of simulation test the mode is again changed to ONNET.
4. Conclusions
Research and development on the equipment are still
active, especially in the power management schemes to
be applied. In future we hope to be able to present more
contributions in this direction. However, in order to be
able to analyze the operation also off-line, a model of the
system was created and is now under evaluation. It can
serve as a good study and analysis tool. Next steps in its
development will include the possibility of use in HIL
(Hardware-In-the-Loop) and SIL (Software-In-the-Loop)
systems. The model has to be improved further by ex-
tending the dynamic model from the currently used linear
approximation to the non-linear representation. It was
also considering the creation of a simple interface for the
introduction of s-functions. In practice it is often impos-
sible to measure them, especially because the currents
into the DC-link capacitors would have to be measured.
Transformation values obtained from the input currents
or other (converter-internal) variables would have to be
used instead. However, use of DC-link currents can be
used in the model of the presented kind, which is a fur-
ther advantage of its use.
Special attention will be given to the development of
the presented system, apart from its main purpose, can be
also used as a valuable research and teaching tool, power
and energy management schemes, with the focus on the
cost functions and introduction of renewable power
sources.
REFERENCES
[1] L. Solero, A. Lidozzi and J. A. Pomilio, “Design of Mul-
tiple-Input Power Converter for Hybrid Vehicles,” IEEE
Trans. on Power Electronics, Vol. 20, No. 5, September
2005, pp. 1007-1015.
[2] P. Pisu and G. Rizzoni, “A Comparative Study Of Super-
visory Control Strategies for Hybrid Electric Vehi-
cles,”IEEE Transactions on Control Systems Technology,
Vol. 15, No. 3, May 2007, pp. 506-518.
[3] H. Dehbonei, S. R. Lee, S. H. Ko and C. V. Nayar, “A
Control Approach and Design Consideration of
PV/Diesel Hybrid Distributed Generation System Using
Dual Voltage Source Inverter for Weak Grid,”
SICE-ICASE International Joint Conference 2006, Oct.
18-2 1, 2006 in Bexco, Busan, Korea, pp. 672-677.
[4] A. Hajizadeh and M. A. Golkar, “Control of Hybrid Fuel
Cell/Battery Distributed Power Generation System with
Voltage Sag Ride-Through Capability,” 2nd IEEE Inter-
national Conference on Power and Energy (PECon 08),
December 1-3, 2008, Johor Baharu, Malaysia, pp.
463-467.
[5] A. Molderink, V. Bakker, J. L. Hurink and G. J. M. Smit,
“Algorithms for Balancing Demand-side Load and Mi-
cro-generation in Islanded Operation,” 19th International
Conference on Systems Engineering, pp. 115-120.
[6] Z. Jiang, “Power Management of Hybrid Photovoltaic -
Fuel Cell Power Systems,” IEEE Power Engineering So-
ciety General Meeting, 18-22 June, 2006, pp. 1-6.
[7] C. Abbey, J. Robinson and G. Joós, “Integrating Renew-
able Energy Sources andSstorage into Isolated Diesel
Generator Supplied Electric Power systems,” EPE-PEMC
2008, 1-3 Sept. 2008, pp. 2178-2183.
[8] J. Zhuo, C. Chakrabarti, K. Lee and N. Chang, “Dynamic
Power Management with Hybrid Power Sources,” in:
44th ACM/IEEE Design Automation Conference, DAC
'07 , 4-8 June 2007, pp. 871-876.
[9] M. E. Torres-Hernández and M. Vélez-Reyes, “Hierar-
chical Control of Hybrid Power Systems,” in: 11th IEEE
International Power Electronics Congress, 2008. CIEP
2008, 24-27 Aug. 2008, pp. 169-176.
[10] A. A. Ferreira, J. A. Pomilio, G. Spiazzi and L. de Araujo
Silva, “Energy Management Fuzzy Logic Supervisory for
Electric Vehicle Power Supplies System,” IEEE Transac-
tions on Power Electronics, Vol. 23, No. 1, January 2008,
pp. 107-115