American Journal of Analyt ical Chemistry, 2011, 2, 9-17
doi:10.4236/ajac.2011.21002 Published Online February 2011 (http://www.SciRP.org/journal/ajac)
Elucidation of Abnormal Potential Responses of
Cation-Selective Electrodes with Solid-State Membranes
to Aqueous Solutions of CuCl2 and CdI2
Yoshihiro Kudo1*, Daisuke Todoroki2, Nobukazu Suzuki2, Naoki Horiuchi1,
Shoichi Katsuta1, Yasuyuki Takeda1
1Graduate School of Sci ence, Chiba University, Chiba, Japan
2Department of Che mistry, Faculty of Science, Chiba University, Chiba, Japan
Received September 9, 2010; revised January 5, 2011; accepted January 10, 2011
Abstract
An empirical solution to abnormal potential responses, showing peaks of emf, of commercial Cu2+- and
Cd2+-selective electrodes with solid-state membranes was proposed for aqueous solutions of CuCl2 and CdI2.
The two-step processes of Mn+ + Yn (s: solid phase) MY(s) and MY(s) + 2X X2MY2(s) (n = 1,
2) at a test solution/electrode-interface were considered as a model. Here, Mn+, Yn, and X refer to a divalent
or univalent cation, functional groups of electrode materials, and a halide ion (X = Cl, Br, I), respectively.
By applying electrochemical potentials to these processes at n = 2, we derived an equation. Regression
analyses based on the equation reproduced well the plots of emf versus log 2(*[M]t) for the Cd(II) and Cu(II)
systems: *[M]t denotes a total concentration of species relevant to M2+ in a bulk of the aqueous solution.
Also, as an apparent selectivity coefficient (Ks) we obtained log Ks(CdBr2) = 4.28  0.22, log Ks(CdI2) = 6.98
 0.05, log Ks(CuCl2) = 3.96  0.09, and log Ks(CuBr2) = 11.4 at 25˚C. The magnitude in log Ks reflected
that in the logarithmic solubility product, log {*[M2+](*[ X ])2}, for bulk water, where *[M2+] or *[X] de-
notes a molar concentration of the bulk solution of M2+ or X at equilibrium, respectively. Moreover, a mix-
ture of CuSO4 with NaCl at the molar ratio of 1:1 yielded a plot similar to that of CuCl2.
 
Keywords: Cation-Selective Electrode, Solid-State Membranes, Potential Response, Solubility Product,
Potentiometry
1. Introduction
Many ion-pair (or complex) formation constants of diva-
lent metal salts (MX2) in water (w) have been determined
so far [1-4]. In the course of potentiometric determina-
tion of these constants for CdI2 and CdBr2 in a bulk w by
using a commercial Cd2+ electrode with a solid-state
membrane [4], plots of the emf versus log 2(*[CdX2]t)
gave peaks, where *[CdX2]t (= *[Cd]t) denotes a total
concentration of CdX2 in the bulk w. Especially, as
shown in Figure 1 of the previous paper [4], a slope of
the plot for the CdI2 system was positive in the lower
range of log 2(*[CdI2]t), while it was negative in its
higher range. As a result, the Cd2+ electrode could not be
used for the determination of the formation constants.
Such plots with the peaks, namely -shaped plots, have
been reported in the cases of potential responses of
cation-selective electrodes with liquid membranes to
some anions, such as F, SCN and ClO4
 [5-7]. Also,
similar potential responses were observed in the case of a
commercial Cu2+ electrode with a solid-state membrane,
when the ion-pair formation of CuCl2 in w had been
studied for the application to solvent-extraction experi-
ments of some Cu(II) salts by crown compounds into
1,2-dichloroethane. The same application has been re-
ported for Cd(II) salts [8].
However, it is difficult to see some models proposed
for elucidating the potential responses of the electrodes
with the liquid membranes [5,7-12] and its elucidation
seems to be unclear [5,7]. The Nicolsky- or Nicolsky-
Eisenman-type equation [9,13] does not reproduce the
-shaped potential responses. Also, some equations de-

10 Y. KUDO ET AL.
rived from the inverted-Nernstian response model based
on the complexation of ionophores with primary and/or
secondary ions [11,12] can not clearly express the re-
sponses.
In the present paper, we tried the reproduction of the
above plots by introducing a model with two-step proc-
esses around the electrode/solution interface, in addition
to ion-pair formation. Applying an electrochemical po-
tential to these processes, we derived an equation and
thereby reproduced the -shaped plot of the CdI2 system.
Also, plots similar to that of the CdX2 system (X = Cl to
I) were observed in CuX2 (Cl, Br) and CaX2 systems (Cl
to I). Furthermore, properties of commercial ISEs, Cd2+
and Cu2+ electrodes with solid-state membranes and Ca2+
one with a liquid membrane, were examined using an
apparent selectivity coefficient (Ks) obtained at 25˚C from
the analyses of these plots by the derived equation. Addi-
tionally, the equation was extended to potential responses
of M+-selective electrodes.
2. Experimental
2.1. Chemicals
Purities of CuCl22H2O (guaranteed pure, Kanto), CuBr2
(guaranteed pure, Kanto), CuSO45H2O (guaranteed pure,
Wako), CaBr2 (98%, degree of hydration  1, Aldrich),
and CaI2nH2O (99.5%, n = 3 to 4, Wako) were deter-
mined by chelatometric titration with EDTA [4]. NaCl
(99.99%, Wako) and KCl ( 99.8%, Kanto) were pre-
pared from the procedures described in a previous paper
[14]. Other chemicals were used without any purification.
Tap water was distilled once and then deionized by
passing through a Milli-Q Lab System. This water was
used for preparing all aqueous solutions.
2.2. Instruments
As the commercial ISEs, the Cu2+ electrode (Horiba, type
8006-10C) with the solid-state membrane and the Ca2+
electrode (Horiba, type 8203-10C) with the liquid mem-
brane were employed. The emf values were measured
with a Horiba pH/ion meter F23 equipped with the ISE
and a reference electrode (Horiba, type 2565A-10T) [4,
15].
2.3. Emf Measurements
Emf values were measured at 25  0.3˚C in the following
cell: AgAgCl0.1 molL1 KCl or NaCl 1 molL1
KNO3test solutionISE [4]. As the test solutions,
aqueous solutions of CuCl2, CuBr2, CaBr2, CaI2, NaCl,
and mixtures of CuSO4 with NaCl were used. As a result
of computation by the Henderson equation, the liquid
junction potentials (< 3 mV) at the 1 molL−1 KNO3test
solution-interface were neglected [4]: this shows that the
aqueous solution of 1 molL−1 KNO3 adequately func-
tions as a salt bridge. The mixtures were prepared by
mixing 0.5006 molL−1 of CuSO4 with 0.5007 molL1 of
NaCl at given volume-ratios.
3. Results and Discussion
3.1. Log *[X]t-Dependence of Emf
Figure 1 shows the dependence of the experimental emf-
values on the log *[X]t ones for (a) the CuX2 (X = Cl,
Br), (b) CdX2, and CaX2 (Br, I) systems. Here, *[X]t de-
notes a total concentration of species relevant to X in
the bulk w and equals 2(*[MX2]t). Therefore, this rela-
tion indicates that the plots of emf versus log *[X]t are
actually equivalent with those versus log {2(*[MX2]t)} in
Figures 1 and 2 {see Equations (10) & (10a)} and ac-
cordingly the plots become showed the log (*[MX2]t)-
dependence of emf with a constant deviation of log 2.
Except for the CuBr2 system, these plots had positive
slopes of 26 to 37 mV/decade in the lower log *[X]t
ranges, showing the Nernstian responses of the elec-
trodes, and then became the lower or negative slopes in
the higher ranges. Only the negative slope was observed
for the CuBr2 system (open diamond in Figure 1(a))
under the present experimental conditions. Its value
shows that the Cu2+ electrode used can act as a selective
electrode for Br, as suggested on its instruction manual.
Also, the fact means that, even in the lower log *[X]t
range, its solid-state membrane more-preferentially in-
teracts with Br than does with Cu2+.
Peaks in emf seemed to shift into the higher values of
log *[X]t in the order X = I < Br < Cl for the MX2 sys-
tems employed (Figure 1). In going from X = Br to I,
their peaks were well-defined for the Cd(II) system
(Figure 1(b)), while, in going from Cl to Br, those was
less-defined for the Cu(II) system (Figure 1(a)).
3.2. Contribution of Ion-Pair Formation to the
Plots of Emf versus Log *[X]t
Only the Nernstian slopes of about 30 mV/decade have
been observed in calibration curves for the aqueous solu-
tions of Cd(NO3)2 with 0.1 molL−1 KNO3 (as an adjuster
of ionic strength, I ), CuSO4 with 0.1 molL1 KNO3, and
CaCl2 with 0.1 molL1 KCl, as shown in the figures of
their instruction manuals. These facts indicate that the
ion-pair (or complex) formation for these salts at I = 0.1
molL1 with KX (X = NO3
, Cl) does not practically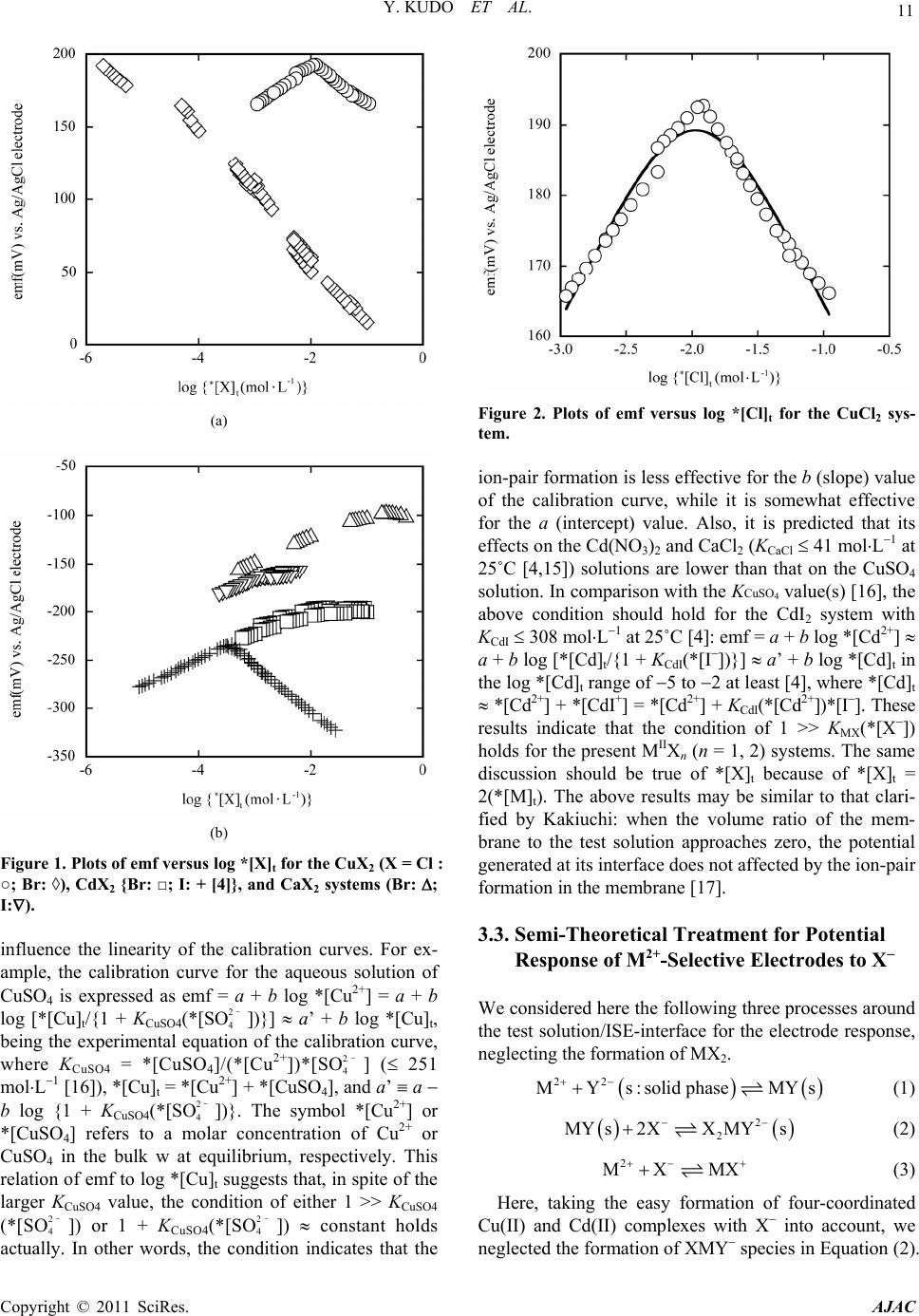

Y. KUDO ET AL.
11
(a)
(b)
Figure 1. Plots of emf versus log *[X]t for the CuX2 (X = Cl :
○; Br: ◊), CdX2 {Br: □; I: + [4]}, and CaX2 systems (Br: ;
I:).
influence the linearity of the calibration curves. For ex-
ample, the calibration curve for the aqueous solution of
CuSO4 is expressed as emf = a + b log *[Cu2+] = a + b
log [*[Cu]t/{1 + KCuSO4(*[SO2–
4])}]  a’ + b log *[Cu]t,
being the experimental equation of the calibration curve,
where KCuSO4 = *[CuSO4]/(*[Cu2+])*[SO2–
4] ( 251
molL1 [16]), *[Cu]t = *[Cu2+] + *[CuSO4], and a’  a 
b log {1 + KCuSO4(*[SO2–
4])}. The symbol *[Cu2+] or
*[CuSO4] refers to a molar concentration of Cu2+ or
CuSO4 in the bulk w at equilibrium, respectively. This
relation of emf to log *[Cu]t suggests that, in spite of the
larger KCuSO4 value, the condition of either 1 >> KCuSO4
(*[SO2–
4]) or 1 + KCuSO4(*[SO2– 4])  constant holds
actually. In other words, the condition indicates that the
Figure 2. Plots of emf versus log *[Cl]t for the CuCl2 sys-
tem.
ion-pair formation is less effective for the b (slope) value
of the calibration curve, while it is somewhat effective
for the a (intercept) value. Also, it is predicted that its
effects on the Cd(NO3)2 and CaCl2 (KCaCl  41 molL1 at
25˚C [4,15]) solutions are lower than that on the CuSO4
solution. In comparison with the KCuSO4 value(s) [16], the
above condition should hold for the CdI2 system with
KCdI  308 molL1 at 25˚C [4]: emf = a + b log *[Cd2+] 
a + b log [*[Cd]t/{1 + KCdI(*[I])}]  a’ + b log *[Cd]t in
the log *[Cd]t range of 5 to 2 at least [4], where *[Cd]t
 *[Cd2+] + *[CdI+] = *[Cd2+] + KCdI(*[Cd2+])*[I]. These
results indicate that the condition of 1 >> KMX(*[X])
holds for the present MIIXn (n = 1, 2) systems. The same
discussion should be true of *[X]t because of *[X]t =
2(*[M]t). The above results may be similar to that clari-
fied by Kakiuchi: when the volume ratio of the mem-
brane to the test solution approaches zero, the potential
generated at its interface does not affected by the ion-pair
formation in the membrane [17].
3.3. Semi-Theoretical Treatment for Potential
Response of M2+-Selective Electrodes to X
We considered here the following three processes around
the test solution/ISE-interface for the electrode response,
neglecting the formation of MX2.


22
MYs:solid phaseMYs



(1)


2
2
MYs2XX MYs




(2)
2
MX MX



(3)
Here, taking the easy formation of four-coordinated
Cu(II) and Cd(II) complexes with X into account, we
neglected the formation of XMY species in Equation (2).

12 Y. KUDO ET AL.
For the overall process of the electrode processes (1) and
(2), therefore, the corresponding equilibrium-constant
was defined as


2
222
2ss
2
22 2
2ss
XMYM YX
XMYYMX
K
 






(4)
and those for the process (1) to (3) were


22
1ss
MY MYK

 , (1a)

2
2
22 s
s
XMYMY XK
 
 



(2a)
and

+2
MX
+2
MXM X
*MX*M*X,
K





(3a)
where [j] and *[j] refer to molar concentrations of spe-
cies j (= M2+, MX+, X) around the electrode interface
and j in a bulk of the test solution, respectively. The
subscript (or superscript) “s” means the solid phase of
the electrode and can be replaced by “o”, which means
an organic phase, for the liquid membrane ISE. We used
here the molar concentrations instead of the activities,
because they render the theoretical treatment compli-
cated and also the experimental calibration curves keep
linearity in the ranges of 10−5 (or 10−6) to 10−1 molL−1
for Cu2+ in w, 10−6 to 10−1 molL−1 for Cd2+, and 2.5 
10−5 to 0.25 (or 1) molL−1 for Ca2+, as shown in the
specifications [18-20] of a Website.
The above electrode processes (1) and (2) at the inter-
face were also expressed by electrochemical potentials
(

) as follows.
ss
MY MY

  (1b)
s
MYX X2MY
2  
s
(2b)
Arranging Equations (1b) and (2b) by the properties of

[21], we have easily
0s 00s
s2 YMMY
YM ln M
22
RT
F
F



 
 

(5)
0
YM ln M
2
RT 2
F




 

 (5a)
0s0 0s
sX2MYXMY
X2MY X2
2ln
22
RT
K
F
F



 (6)
0
X2MY X2
ln
2
RT
K
F
  . (6a)
Here, 
j, 0
j
j


, and 0
j

denote an inner potential
for the species j (= M2+, Y2, X2MY2) in each phase, a
standard electrode potential, and a standard chemical
potential corresponding to j, respectively. R, T and F
have the usual meanings. By the sum of Equations (5a)
and (6a), we could express the emf value in question as
020
YMX2MYX 2
emfln Mln
22
RT RT
K
F
F



 
 . (7)
Also, the following relations were derived from mass
balance equations around the test solution/electrode-
interface.





22
2
ts
s
22
2s
2
22
s
MMMXMYX MY
MMXXMY
M1YXK

 



 
 

 
 
 
 
 

 
(8)
by assuming that 1 >> K2[X]2 and then 1 + K[Y2]s[X]2
>> KMX[X] (see above for 1 >> KMX[X]) and



2
2
ts
222
MX s
XX MX2XMY
X1M2YMX
X
KK
g
 


 
 
 



 





(8a)
with g = 1 + KMX[M2+] + 2K[Y2]s[M2+][X]. Rearrang-
ing Equation (8) as





*
M
2t
2
2
st
*
M
t
2
*
2
2
X
st
M
M
1Y X
M
1Y X
D
Kg
D
KDg





 







(9)
with DM = [M]t/*[M]t { ([M2+] + [MX+] + [MY]s +
[X2MY2]s)/(*[M2+] + *[MX+])} and DX = [X]t/*[X]t {
([X] + [MX+] + 2[X2MY2]s)/(*[X] + *[MX+])} and
then introducing Equation (9) into Equation (7), we have
easily




*
00 m
YM X2MYXt
2
*
st
emflnln X
222
ln1X
2
K RT RT
FF
RT K
F
  

(10)




*
00
YM X2MYXmt
2
*
st
lnln M
22
ln14M
2
RT RT
K
FF
RT K
F
  

(10a)
with DMK2 = Km, K[Y2]s(DX/g)2 {= K[Y2]s([X]/*[X]t)2
= ([X2MY2]s/[M2+]) /(* [X]t)2} = Ks, and *[X]t = 2(*[M]t)
{= 2(*[MX2]t)}. Here, the DM and DX values like distri-
bution ratios at the test solution/electrode-interface were
assumed to be much smaller than unity and the term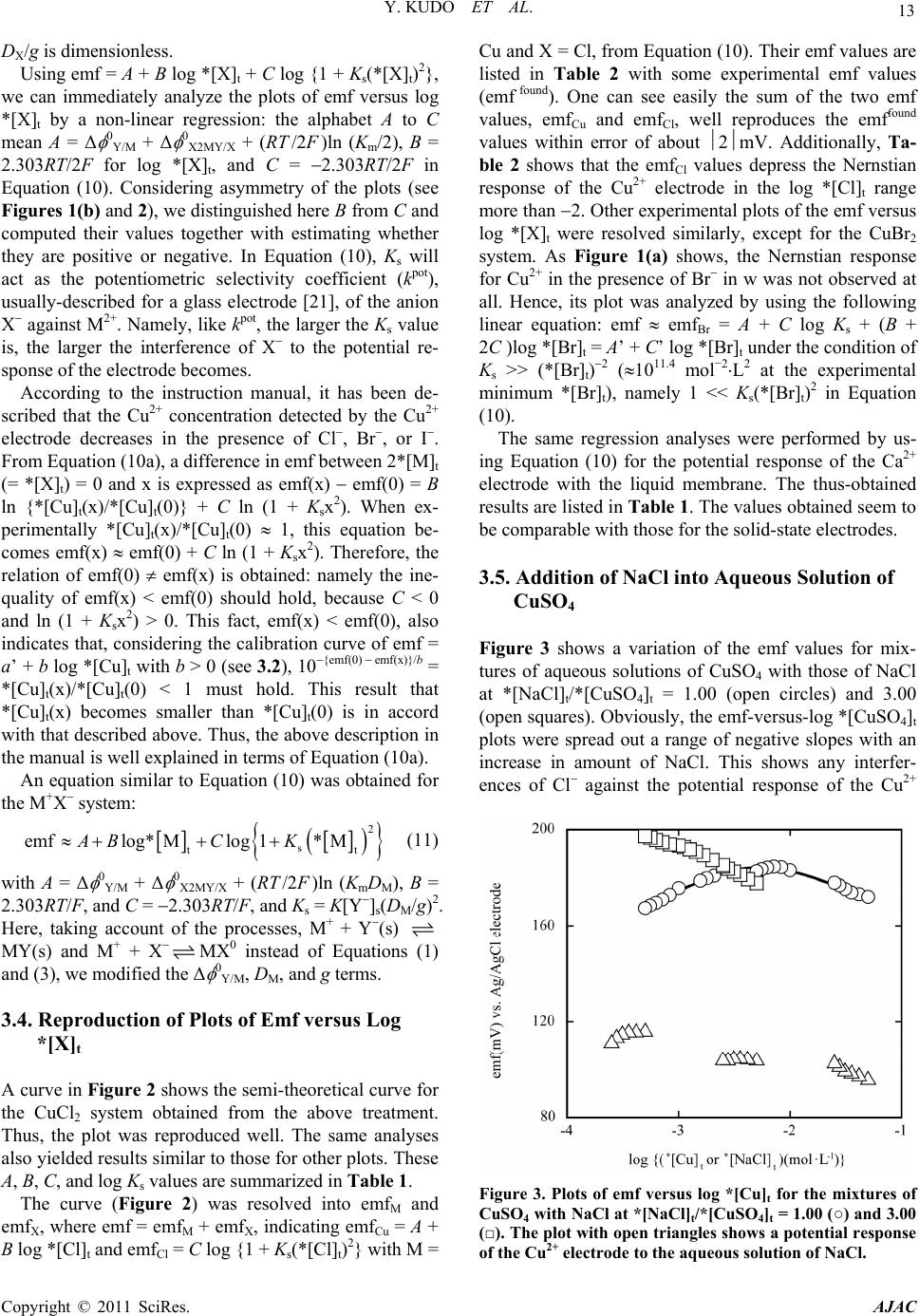

Y. KUDO ET AL.
13
DX/g is dimensionless.
Using emf = A + B log *[X]t + C log {1 + Ks(*[X]t)2},
we can immediately analyze the plots of emf versus log
*[X]t by a non-linear regression: the alphabet A to C
mean A = Δ 
0
Y/M + Δ

0
X2MY/X + (RT /2F )ln (Km/2), B =
2.303RT/2F for log *[X]t, and C = 2.303RT/2F in
Equation (10). Considering asymmetry of the plots (see
Figures 1(b) and 2), we distinguished here B from C and
computed their values together with estimating whether
they are positive or negative. In Equation (10), Ks will
act as the potentiometric selectivity coefficient (kpot),
usually-described for a glass electrode [21], of the anion
X against M2+. Namely, like kpot, the larger the Ks value
is, the larger the interference of X to the potential re-
sponse of the electrode becomes.
According to the instruction manual, it has been de-
scribed that the Cu2+ concentration detected by the Cu2+
electrode decreases in the presence of Cl, Br, or I.
From Equation (10a), a difference in emf between 2*[M]t
(= *[X]t) = 0 and x is expressed as emf(x)  emf(0) = B
ln {*[Cu]t(x) /* [ Cu ] t(0)} + C ln (1 + Ksx2). When ex-
perimentally *[Cu]t(x)/*[Cu]t(0)  1, this equation be-
comes emf(x)  emf(0) + C ln (1 + Ksx2). Therefore, the
relation of emf(0)  emf(x) is obtained: namely the ine-
quality of emf(x) < emf(0) should hold, because C < 0
and ln (1 + Ksx2) > 0. This fact, emf(x) < emf(0), also
indicates that, considering the calibration curve of emf =
a’ + b log *[Cu]t with b > 0 (see 3.2), 10{emf(0)  emf(x)}/b =
*[Cu]t(x)/*[Cu]t(0) < 1 must hold. This result that
*[Cu]t(x) becomes smaller than *[Cu]t(0) is in accord
with that described above. Thus, the above description in
the manual is well explained in terms of Equation (10a).
An equation similar to Equation (10) was obtained for
the M+X system:
 


2
s
tt
emflog* Mlog1* MABC K  (11)
with A = Δ

0
Y/M + Δ

0
X2MY/X + (RT /2F )ln (KmDM), B =
2.303RT/F, and C = 2.303RT/F, and Ks = K[Y]s(DM/g)2.
Here, taking account of the processes, M+ + Y(s)
MY(s) and M+ + XMX0 instead of Equations (1)
and (3), we modified the Δ

0
Y/M, DM, and g terms.


3.4. Reproduction of Plots of Emf versus Log
*[X]t
A curve in Figure 2 shows the semi-theoretical curve for
the CuCl2 system obtained from the above treatment.
Thus, the plot was reproduced well. The same analyses
also yielded results similar to those for other plots. These
A, B, C, and log Ks values are summarized in Table 1.
The curve (Figure 2) was resolved into emfM and
emfX, where emf = emfM + emfX, indicating emfCu = A +
B log *[Cl]t and emfCl = C log {1 + Ks(*[Cl]t)2} with M =
Cu and X = Cl, from Equation (10). Their emf values are
listed in Table 2 with some experimental emf values
(emf found). One can see easily the sum of the two emf
values, emfCu and emfCl, well reproduces the emffound
values within error of about 2mV. Additionally, Ta-
ble 2 shows that the emfCl values depress the Nernstian
response of the Cu2+ electrode in the log *[Cl]t range
more than 2. Other experimental plots of the emf versus
log *[X]t were resolved similarly, except for the CuBr2
system. As Figure 1(a) shows, the Nernstian response
for Cu2+ in the presence of Br in w was not observed at
all. Hence, its plot was analyzed by using the following
linear equation: emf  emfBr = A + C log Ks + (B +
2C )log *[Br]t = A’ + C’ log *[Br]t under the condition of
Ks >> (*[Br]t)2 (1011.4 mol−2L2 at the experimental
minimum *[Br]t), namely 1 << Ks(*[Br]t)2 in Equation
(10).
The same regression analyses were performed by us-
ing Equation (10) for the potential response of the Ca2+
electrode with the liquid membrane. The thus-obtained
results are listed in Table 1. The values obtained seem to
be comparable with those for the solid-state electrodes.
3.5. Addition of NaCl into Aqueous Solution of
CuSO4
Figure 3 shows a variation of the emf values for mix-
tures of aqueous solutions of CuSO4 with those of NaCl
at *[NaCl]t/*[CuSO 4]t = 1.00 (open circles) and 3.00
(open squares). Obviously, the emf-versus-log *[CuSO4]t
plots were spread out a range of negative slopes with an
increase in amount of NaCl. This shows any interfer-
ences of Cl against the potential response of the Cu2+
Figure 3. Plots of emf versus log *[Cu]t for the mixtures of
CuSO4 with NaCl at *[NaCl]t/*[CuSO4]t = 1.00 (○) and 3.00
(□). The plot with open triangles shows a potential response
of the Cu2+ electrode to the aqueous solution of NaCl.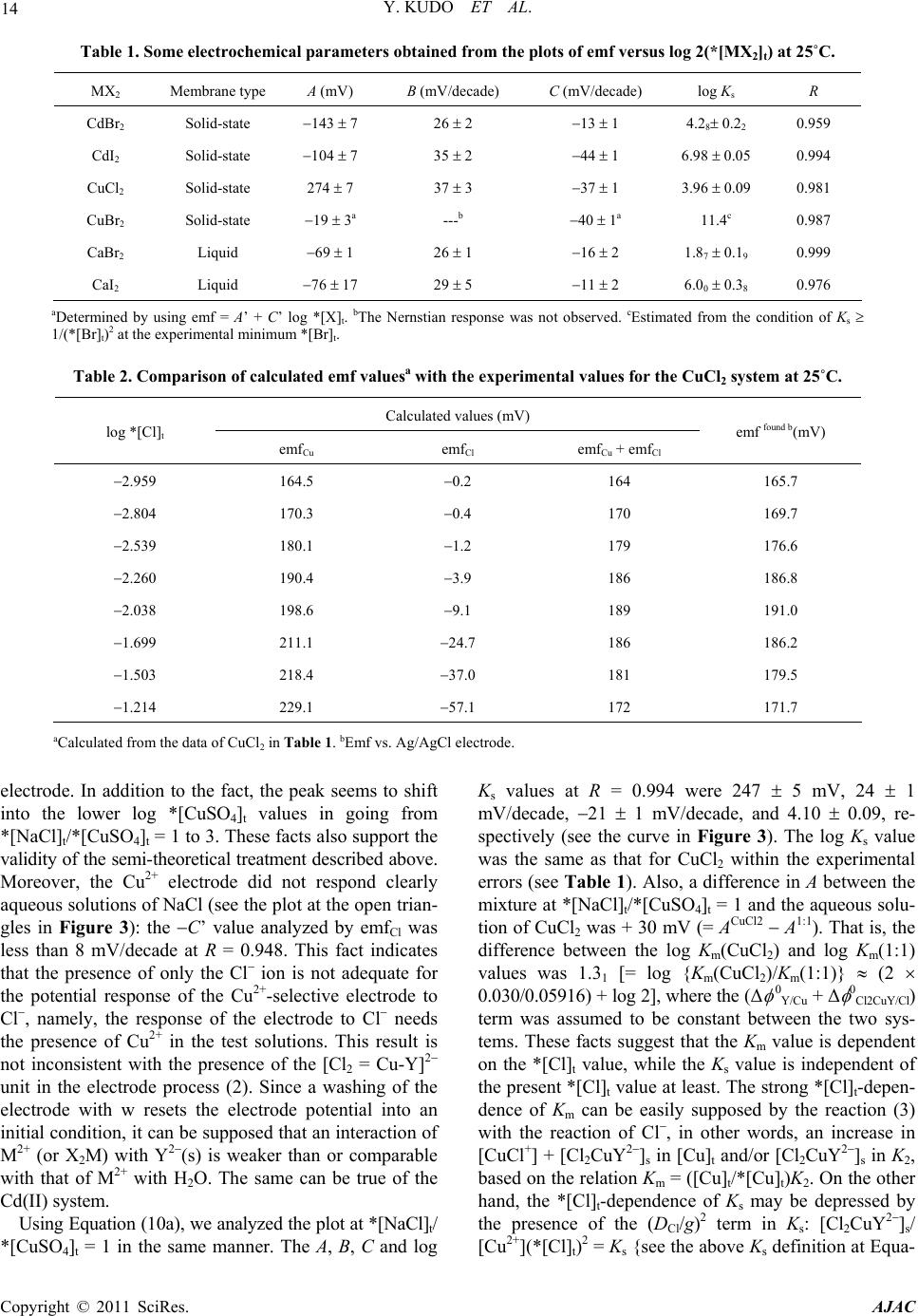

Y. KUDO ET AL.
14
Table 1. Some electrochemical parameters obtained from the plots of emf versus log 2(*[MX2]t) at 25˚C.
MX2 Membrane type A (mV) B (mV/decade) C (mV/decade) log Ks R
CdBr2 Solid-state 143  7 26  2 13  1 4.28 0.22 0.959
CdI2 Solid-state 104  7 35  2 44  1 6.98  0.05 0.994
CuCl2 Solid-state 274  7 37  3 37  1 3.96  0.09 0.981
CuBr2 Solid-state 19  3a ---b 40  1a 11.4c 0.987
CaBr2 Liquid 69  1 26  1 16  2 1.87  0.19 0.999
CaI2 Liquid 76  17 29  5 11  2 6.00  0.38 0.976
aDetermined by using emf = A’ + C’ log *[X]t. bThe Nernstian response was not observed. cEstimated from the condition of Ks 
1/(*[Br]t)2 at the experimental minimum *[Br]t.
Table 2. Comparison of calculated emf valuesa with the experimental values for the CuCl2 system at 25˚C.
Calculated values (mV)
log *[Cl]t
emfCu emfCl emfCu + emfCl
emf found b(mV)
2.959 164.5 0.2 164 165.7
2.804 170.3 0.4 170 169.7
2.539 180.1 1.2 179 176.6
2.260 190.4 3.9 186 186.8
2.038 198.6 9.1 189 191.0
1.699 211.1 24.7 186 186.2
1.503 218.4 37.0 181 179.5
1.214 229.1 57.1 172 171.7
aCalculated from the data of CuCl2 in Table 1. bEmf vs. Ag/AgCl electrode.
electrode. In addition to the fact, the peak seems to shift
into the lower log *[CuSO4]t values in going from
*[NaCl]t/*[CuSO4]t = 1 to 3. These facts also support the
validity of the semi-theoretical treatment described above.
Moreover, the Cu2+ electrode did not respond clearly
aqueous solutions of NaCl (see the plot at the open trian-
gles in Figure 3): the C’ value analyzed by emfCl was
less than 8 mV/decade at R = 0.948. This fact indicates
that the presence of only the Cl ion is not adequate for
the potential response of the Cu2+-selective electrode to
Cl, namely, the response of the electrode to Cl needs
the presence of Cu2+ in the test solutions. This result is
not inconsistent with the presence of the [Cl2 = Cu-Y]2
unit in the electrode process (2). Since a washing of the
electrode with w resets the electrode potential into an
initial condition, it can be supposed that an interaction of
M2+ (or X2M) with Y2(s) is weaker than or comparable
with that of M2+ with H2O. The same can be true of the
Cd(II) system.
Using Equation (10a), we analyzed the plot at *[NaCl]t/
*[CuSO4]t = 1 in the same manner. The A, B, C and log
Ks values at R = 0.994 were 247  5 mV, 24  1
mV/decade, 21  1 mV/decade, and 4.10  0.09, re-
spectively (see the curve in Figure 3). The log Ks value
was the same as that for CuCl2 within the experimental
errors (see Table 1). Also, a difference in A between the
mixture at *[NaCl]t/*[CuSO4]t = 1 and the aqueous solu-
tion of CuCl2 was + 30 mV (= ACuCl2  A1:1). That is, the
difference between the log Km(CuCl2) and log Km(1:1)
values was 1.31 [= log {Km(CuCl2)/Km(1:1)}  (2 
0.030/0.05916) + log 2], where the (Δ 
0
Y/Cu + Δ

0
Cl2CuY/Cl)
term was assumed to be constant between the two sys-
tems. These facts suggest that the Km value is dependent
on the *[Cl]t value, while the Ks value is independent of
the present *[Cl]t value at least. The strong *[Cl]t-depen-
dence of Km can be easily supposed by the reaction (3)
with the reaction of Cl, in other words, an increase in
[CuCl+] + [Cl2CuY2]s in [Cu]t and/or [Cl2CuY2]s in K2,
based on the relation Km = ([Cu]t/*[Cu]t)K2. On the other
hand, the *[Cl]t-dependence of Ks may be depressed by
the presence of the (DCl/g)2 term in Ks: [Cl2CuY2]s/
[Cu2+](*[Cl]t)2 = Ks {see the above Ks definition at Equa-

Y. KUDO ET AL.
15
tions (10) and (10a)}.
3.6. Application of the Present Model to Other
Liquid Membrane ISEs
In the same manner as that (see 3.4) for the potential
responses measured by the commercial Ca2+ electrode,
we analyzed data [5] reported by Morf and Simon for a
potential response of the neutral carrier-based Ca2+ elec-
trode with o-nitrophenyl octyl ether to an aqueous solu-
tion of Ca(SCN)2. The A, B, C, and log Ks values at R =
0.998 were > (85  5) mV, 18  1 mV/decade, 22  2
mV/decade, and 4.27  0.22, respectively (from Figure 1
in [5]). Also, data [7] reported by Egorov and Lushchik
for the potential response of a H+ electrode based on a
neutral amine-type carrier in dioctyl phthalate-PVC
membrane to the hydrofluoric acid solution was analyzed
by using Equation (11): A > (233  21) mV, B = 74  7
mV/decade, C = 67  5 mV/decade, and log Ks = 4.09 
0.19 at R = 0.991 (from Figure 4 in [7]). The same val-
ues were obtained from the analysis with Equation (17)
[7] proposed by them: emf = A + B log aH+ + (C/2) log
{2Kex(aH+)2 + (Kex)2(aH+)4 + 1} under the conditions of
aH+ = aF and tot tot
Am R
CC and then this equation is eas-
ily arranged into A + B log aH+ + C log {Kex(aH+)2 + 1},
being equivalent to Equation (11). Here, aj ( j = H+, F),
tot
Am
C, and tot
R
C denote an activity of j in the test solu-
tion, total concentrations of amine (Am) and a lipophilic
univalent anion R included in a liquid membrane, re-
spectively. The term Kex is an extraction constant
(mol2L2) of H+F by Am into the liquid membrane and
so corresponds to the Ks value in unit. At least, the re-
sults for the two Ca2+ electrodes suggest essential simi-
larity in model between the solid-state membrane ISE
and the liquid membrane ISE [7,9]. Also, a model sug-
gesting the formation of X2MY2 in a liquid membrane
has been proposed [12], where Y2 means a basic iono-
phore. However, its detailed description was not found
[12]. Furthermore, another model with the formation of
XMIY(s) in Equation (2) could reproduce the -shaped
plot at R = 0.983 for the above H+ electrode. This R value
was smaller than that (0.991) of the model with
X2MIY2(s), showing the advantage of the X2MY2(s)
formation.
3.7. X Concentration at Peak Potential
The concentration (*[X]t
peak) at the peak potential was
estimated from the derivative of Equation (10) under the
condition of


*
t
0
X
demf
d, where


*
t
X
demf
d = B/*[X]t
+ 2CKs(*[X]t)/{1 + Ks(*[X]t)2} and then *[X]t
peak =

s
2
B
BCK

 {= 2(*[M]t
peak) for Equation (10a)}. The
*[X]t
peak values were 2.6  10−4 and 0.010 mol L−1 for the
CdI2 and CuCl2 systems, respectively. These values are
in good agreement with those of the peaks shown in
Figures 1 and 2. The same result was also obtained for
the Ca(SCN)2 system with the experimental log *[Ca]t
peak
of about 2.5 [5]. Similarly, the log *[HF]t
peak value (=
2.0) was in good agreement with the experimental up-
per limit of the proton response [7]. These results indi-
cate well the reproducibility of the plots based on Equa-
tions (10) and (11).
3.8. For Properties of the M2+ Electrodes
Employed
The Ks values were calculated to be {Ks(CdCl2) <}
Ks(CdBr2) < Ks(CdI2). This fact indicates that the selec-
tivity of the Cd2+ electrode (Horiba, type 8007-10C with
a solid-state membrane) against X is in the order X = I
< Br < Cl. The same is partly true of the Cu2+ electrode
(type 8006-10C): Ks(CuCl2) << Ks(CuBr2) (Table 1).
Predicting [j]s (j = Y2, X2MY2) to be unity in Equation
(4), then the log Ks value can be proportional to the
logarithmic solubility product, log Ksp [=log {*[M2+]
(*[X])2}]. From solubility (S) data [22] at 25˚C in w, the
estimated values were in the orders CdI2 {log (Ksp/mol3
L3) = log 4S 3 = 0.908} < CdBr24H2O (1.162) < CdCl2
(5/2)H2O (1.739) and CuBr2 (1.795)  CuCl22H2O (1.801),
where it was assumed that 100 g of aqueous solutions
equals 0.100 L and then the S data in a %(w/w) unit was
converted to that in a mol L−1 one. This order suggests
that the smaller the log Ksp(MX2) value is, the more easy
MX2 interacts with the electrode, and then the larger the
interference of X against the electrode becomes. The
same discussion can hold for the CaX2 system with the
liquid membrane, as follows. The log Ksp(CaX2) values
in w at 25˚C were estimated to be 1.549 for CaCl26H2O,
1.482 for CaBr26H2O, 1.293 for CaI26H2O, and 1.865 for
Ca(NCS)24H2O from the S data [22]. The log Ksp order
for X = Cl, Br and I was in good agreement with the log
Ks one, although the log Ks(CaCl2) value could not be
determined. A deviation of the Ca(SCN)2 system from
the order suggests that an incorporation of Ca2+ in com-
plex formation with the neutral carrier (L) around the test
solution/liquid membrane-interface strongly contributes
an increase in Ks, namely a transfer of CaL2+, XCaL+,
X2CaL and so on [8] into the o phase.
4. Conclusion
It was demonstrated that the present model based on the

16 Y. KUDO ET AL.
balances among the electrochemical potentials reproduce
well the potential responses of the commercial Cd2+ and
Cu2+ electrodes with the solid-state membranes in the
presence of only the counter halide ions. Also, one could
see that the phenomena for the Ca2+ and H+ electrodes
with the liquid membranes are similarly treated. These
facts suggest that the present model contains essential
processes being important for the potential responses of
electrodes with liquid membranes at least. Further stud-
ies will be required for this agreement in potential re-
sponse between the electrodes with the solid-state mem-
branes and those with the liquid membranes, because the
latter electrodes respond under the more-complicated
experimental conditions. Not taking account of so-called
interfering ions in the test solutions, Equations (10) and
(10a) do not reach the general equations derived before.
However, Equations (10) and (10a) could directly esti-
mate the parameters, Ks and A (with Km). By these equa-
tions, one can relate properties of the M2+ and M+ elec-
trodes with Ksp, although their applications are limited to
the solid-state membrane ISEs showing the -shaped
potential responses.
5. References
[1] D. N. Hume, D. D. DeFord and G. C. B. Cave, “A Pola-
rographic Study of the Cadmium Thiocyanate Com-
plexes,” Journal of American Chemical Society, Vol. 73,
1951, pp. 5323-5325. doi:10.1021/ja01155a094
[2] C. E. Vanderzee and H. J. Dawson Jr., “The Stability
Constants of Cadmium Chloride Complexes: Variation
with Temperature and Ionic Strength,” Journal of
American Chemical Society, Vol. 75, 1953, pp. 5659-
5663. doi:10.1021/ja01118a056
[3] P. Gerding, “Thermochemical Studies on Metal Com-
plexes I. Free Energy, Enthalpy, and Entropy Changes for
Stepwise Formation of Cadmium(II) Halide Complexes
in Aqueous Solution at 25˚C,” Acta Chimca Scandinavica,
Vol. 20, No. 1, 1966, pp. 79-94.
doi:10.3891/acta.chem.scand.20-0079
[4] Y. Kudo, D. Todoroki, N. Horiuchi, S. Katsuta and Y.
Takeda, “Ion-Pair Formation of Sodium Salts of Several
Oxo Anions and Cadmium Halides in Water and the Dis-
tribution of Monovalent Sulfate Ion Pairs in Nitroben-
zene,” Journal of Chemical and Engineering Data, Vol.
55, No. 7, 2010, pp. 2463-2469.
doi:10.1021/je900861h
[5] W. E. Morf and W. Simon, “Cation-Response Mecha-
nism of Neutral Carrier Based Ion-Selective Electrode
Membranes,” Helvetica Chimica Acta, Vol. 69, 1986, pp.
1120-1131. doi:10.1002/hlca.19860690520
[6] E. Lindner, E. Gráf, Z. Niegreisz, K. Tóth, E. Pungor and
R. P. Buck, “Responses of Site-Controlled, Plasticized
Membrane Electrodes,” Analytical Chemistry, Vol. 60,
No. 4, 1988, pp. 295-301. doi:10.1021/ac00155a004
[7] V. V. Egorov and Y. F. Lushchik, “H+-Selective Elec-
trodes Based on Neutral Carriers: Specific Features in
Behaviour and Quantitative Description of the Electrode
Response,” Talanta, Vol. 37, No. 5, 1990, pp. 461-469.
doi:10.1016/0039-9140(90)80071-M
[8] Y. Kudo, Y. Kobayashi, S. Katsuta and Y. Takeda, “Ion-
pair Formation of Cadmium-18-Crown-6 Ethers Complex
Ions with Picrate and Chloride Ions in Water and Distri-
bution of Its Picrate Ion-pair Complexes into Benzene,”
Journal of Molecular Liquids, Vol. 146, 2009, pp. 60-65.
doi:10.1016/j.molliq.2009.02.004
[9] T. Kakiuchi and M. Senda, “The Theory of Liquid Ion
Exchange Membrane Ion-Selective Electrodes Based on
the Concept of the Mixed Ion-Transfer Potential,” Bulle-
tin of the Chemical Society of Japan, Vol. 57, No. 7, 1984,
pp. 1801-1808. doi:10.1246/bcsj.57.1801
[10] A . Jyo, K. Fukamachi, W. Koga and N. Ishibashi, “The
Influence of a Co-ion on the Potential of a Liquid
-Exchanger Membrane Electrode,” Bulletin of the
Chemical Society of Japan, Vol. 50, No. 3, 1977, pp.
670-672. doi:10.1246/bcsj.50.670
[11] P. Bühlmann and Y. Umezawa, “Apparently ‘Non-Nern-
stian’ Equilibrium Responses Based on Complexation
Between the Primary Ion and a Secondary Ion in the Liq-
uid ISE Membrane,” Electroanalysis, Vol. 11, No. 10-11,
1999, pp. 687-693. doi:10.1002/(SICI)1521-4109(199907)
11:10/11<687::AID-ELAN687>3.0.CO;2-C
[12] S. Amemiya, P. Bühlmann and K. Odashima, “A Gener-
alized Model for Apparently ‘Non-Nernstian’ Equilib-
rium Responses of Ionophore-Based Ion-Selective Elec-
trodes. 1. Independent Complexation of the Ionophore
with Primary and Secondary Ions,” Analytical Chemistry,
Vol. 75, No. 14, 2003, pp. 3329-3339.
doi:10.1021/ac026471g
[13] G. D. Christian, “Analytical Chemistry,” 5th Edition,
John Wiley & Sons, New York, 1994, p. 335.
[14] Y. Kudo, R. Fujihara, T. Ohtake, S. Katsuta and Y. Ta-
keda, “Evaluation of the Hydrophilic Property of Sodium
Ion-Pair Complexes with 3m-Crown-m Ethers (m = 5, 6)
and Their Benzo-Derivatives by Solvent Extraction,”
Analytical Sciences, Vol. 24, 2008, pp. 999-1003.
doi:10.2116/analsci.24.999
[15] Y. Kudo, S. Takeuchi, Y. Kobayashi, S. Katsuta and Y.
Takeda, “Potentiometric Determination of Ion-Pair For-
mation Constants for Cadmium, Calcium Salts, and Cad-
mium-18-Crown-6 Ether Derivative Complexes with a
Sulfate Ion in Water,” Journal of Chemical and Engi-
neering Data, Vol. 52, No. 5, 2007, pp. 1747-1752.
doi:10.1021/je700135j
[16] S. Wasylkiewicz, “Ion Association in Aqueous Solutions
of Electrolytes. II. Mathematical Model for Sulphates of
Bivalent Metals,” Fluid Phase Equilibria, Vol. 57, 1990,
pp. 277-296. doi:10.1016/0378-3812(90)85127-V
[17] T. Kakiuchi, “Limiting Behanior in Equilibrium Parti-
tioning of Ionic Components in Liquid-Liquid Two-Phase
Systems,” Analytical Chemistry, Vol. 68, No. 20, 1996,
pp. 3658-3664. doi:10.1021/ac960032y

Y. KUDO ET AL.
17
[18] Internet Available: http://www.horiba.com/us/en/applica-
tion/material-property -characterization/water-analysis/wa-
ter-quality-electrochemistry-instrumentation/electrodes/ion-
electrodes/details/copper-ion-electrode-8006-10c-9511/
[19] Internet Available: http://www.horiba.com/us/en/applica-
tion/material-property -characterization/water-analysis/wa-
ter-quality-electrochemistry-instrumentation/electrodes/ion-
electrodes/details/cadmium-ion-electrode-8007-10c-9515/
[20] Internet Available: http://www.horiba.com/us/en/applica-
tion/material-property-characterization/water-analysis/wa-
ter-quality-electrochemistry-instrumentation/electrodes/ion-
electrodes/details/calcium-ion-electrode-8203-10c-9587/
[21] A. J. Bird and L. R. Faulkner, “Electrochemical Methods:
Fundamentals and Applications,” 2nd Edition, John
Wiley & Sons, New York, 2001, pp. 60-62; 74-81.
[22] K. A. Inaba, S. Takagi, K. Tajima, H. Tohara, K. Naka-
tsuka, K. Nakanishi, H. Nakayama, T. Makita and M.
Muramatsu, “Handbook of Chemistry, Fundamentals II”,
In: H. Chihara, Ed., 3rd Edition, The Chemical Society of
Japan, Maruzen, Tokyo, 1984, pp. II-166; II-177.