Applied Mathematics, 2011, 2, 264-269
doi:10.4236/am.2011.22031 Published Online February 2011 (http://www.SciRP.org/journal/am)
Mathematical Model of Blood Flow in Small Blood
Vessel in the Presence of Magnetic Field
Rekha Bali, Usha Awasthi
Department of Mathematics, Harcourt Butler Technological Institute, Navabganj, India
Received December 14, 2010; revised January 3, 2011; accepted January 8, 2011
Abstract
A mathematical model for blood flow in the small blood vessel in the presence of magnetic field is presented
in this paper. We have modeled the two phase model for the blood flow consists of a central core of sus-
pended erythrocytes and cell-free layer surrounding the core. The system of differential equations has been
solved analytically. We have obtained the result for velocity, flow rate and effective viscosity in presence of
peripheral layer and magnetic field .All the result has been obtained and discussed through graphs.
Keywords: Blood, Plasma, Magnetic Field, Effective Viscosity, Peripheral Layer
1. Introduction
Blood shows anomalous viscous properties. The anoma-
lous behavior of blood is principally due to the suspen-
sion of particles in plasma. The plasma solution in the
blood obeys the linear Newtonian model for viscosity [1].
However, blood as a whole is often considered as non-
Newtonian fluid, particularly when the characteristic di-
mension of the flow is close to the cell dimension. The
experimental observations and theoretical analysis of
blood flow are very useful for the diagnosis of a number
of cardiovascular diseases and development of patho-
logical patterns in animal or human physiology [2]. The
flow of blood through small diameter tubes is of physio-
logical and clinical importance. Due to its complexity and
anomalous behaviour, it is very difficult to analyze it. The
two types of anomaly are due to low shear and high shear
effects [3]. When blood flows through larger diameter ar-
teries at high shear rates, it behaves like a Newtonian
fluid. The apparent viscosity of blood decreases with de-
creasing blood vessel diameter, when measurements are
made in capillaries of diameter less than 300

m [4].
Pries et al. [5] studied the effect of the tube diameter
and the hematocrit ratio on the blood viscosity and found
that for tube diameters greater than 1 mm, the blood vis-
cosity is independent of the diameter while for tube di-
ameter less than 1 mm, the blood viscosity is strongly de-
pendent on the tu be diameter. They also reported the vis-
cosity increases non-linearly with the hematocrit. Bug-
liarello and Sevilla [6], Cokelet [7] and [8-10] have re-
ported that for blood flowing through narrow blood ves-
sels, there is a peripheral layer of plasma and a core re-
gion of suspension of all the erythrocytes.
Also the red blood cell is major bio-magnetic subs-
tance and the blood flow may be influenced by the mag-
netic field [11]. The effect of magnetic field on blood
flow has been analyzed theoretically by treating blood as
an electrically conductive fluid [12]. Assuming blood as
a magnetic fluid, it may be possible to control blood pre-
ssure and its flow behavior by using an appropriate mag-
netic field. Hence such studies have potential for thera-
peutic use in the diseases of heart, blood and blood ves-
sels.
Most of the model [13-17] on blood flow deal with
one phase model. However, in view of the fact that blood
is a suspension, a two-phase model appears to be more
appropriate. Wagh and Wagh [18] have used [19] a mo-
del of dusty gas to study the effect of the magnetic nature
of red blood cells of the flow of blood. The reason is,
blood is a liquid suspension having mass and volume
concentrations roughly the same, however, for dusty gas
the mass and bulk concentrations are quite different [20],
Nayfeh’s [21] two phase model seems to be more suita-
ble for blood flow.
In view of the above mentioned fact, we have consid-
ered the two phase model consisting of central core of
suspended erythrocyte and cell free layer surrounding the
core in the presence of magnetic field.

R. BALI ET AL.
265
2. Mathematical Analysis
We have considered a two layer model (Figure 1) for the
blood flow within cylindrical vessel of radius R consist-
ing of central core radius R1, which contains an erythro-
cyte suspension of uniform hematocrit and a cell free
layer outside the core containing plasma. We have taken
some assumptions for formulating the mathematical mo-
del.
Blood is considered as viscous, incompressible and
electrically conducting fluid. Fluid flow is steady and la-
minar. Magnetic field is constant in transverse direction.
2.1. Governing Equations
Introducing the assumptions mentioned above the go-
verning equation for the fluid flow are given as.
00
10
,
PrRrR
zrr r
u 
 

 

  


(1)
 

2
2
1
01 ff
s
dp f
uu
P
zrr r
Fu u



  
 
 
 

  




 
(2)

0
0dp fp
PdH
Fu ukM
zdz





 




(3)
Where ,rz
 are radial and axial co-ordinate,
f
u
and
p
u are the velocities of the fluid (plasma) and par-
ticles (red cell),

is the volume fraction of the red
cells,

s

 is the suspension viscosity, d
F
is the
drag coefficient of interaction for the force exerted by
one phase on the other, 0
k is the magnetic permeability,
p
M
is the magnetization of red cells and dH
dz


is the
magnetic field gradient. The expression of the drag coef-
ficient is given by:
 


1
22
22
438 33
9,where
223
f
d
FR


 
 


Where
f

is the constant fluid viscosity.
The viscosity of the suspension is given by an empiri-
cal relation.

,when
1
f
s

 
Figure 1. Flow geometry of blood in small vessels.
1107
0.07exp2.49exp( 1.69)
T








2.2. Boundary Conditions
0
0
1
0
0at
0at 0
and at
pf
f
f
urR
uu r
rr
uu
rR









 

 


 

 







(4)
Where 0
00
u
r






and

01
f
s
u
r






2.3. Solutio n o f the Probl em
Introduc ing the following non-dimensional scheme.
1
12
00
00
00 0
00
00
2
00 0
,,,
,,,
,, ,
fp
fp s
e
R rz P
rzRP
Rz R U
uu
uu e
UU Rz
UR u
H
R
RuH
Rz U


























(5)
The expression for the velocities 0
u,
f
u, and
p
u,
obtained as the solution of Equations (1)-(3), subjected to
the boundary conditions are given as:

2
01
1
4e
RP
uR
z




 (6)

 
20
2222 22
11 1
1(1 )1
41 4(1)
ep
e
fs s
RReMk
RPdH
ueRrRR rR
zdz

 
 




 


(7)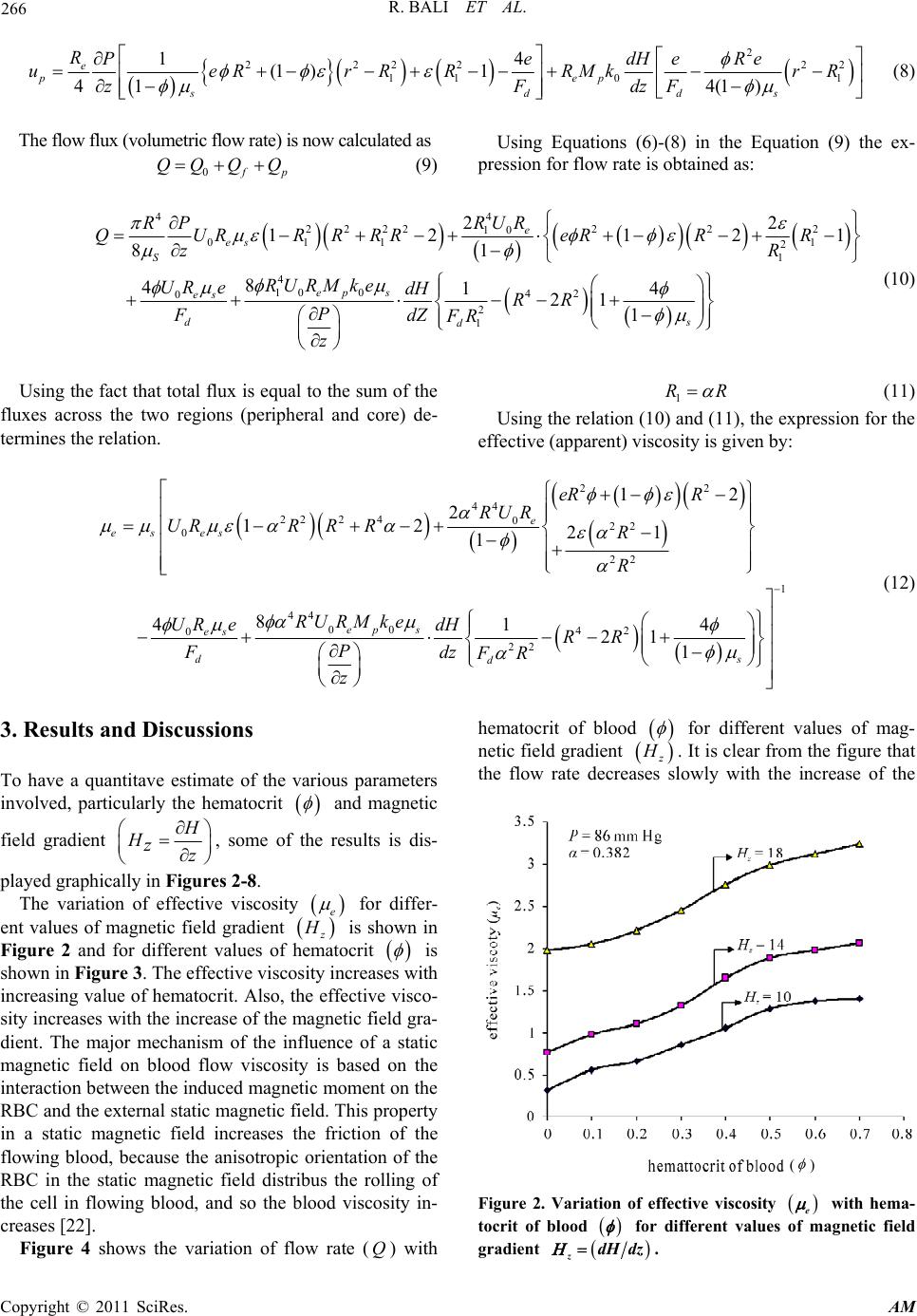

R. BALI ET AL.
266

 
2
2222 22
11 01
14
(1 )1
41 4(1)
e
pep
sdds
RPedHeRe
ueRrRRRMk rR
zFdzF

 
 








 




(8)
The flow flux (volumetric flow rate) is now calculated as
0
f
p
QQ QQ (9) Using Equations (6)-(8) in the Equation (9) the ex-
pression for flow rate is obtained as:
 
 



4
4222222 2
10
011 1
2
1
4
10 042
02
1
22
12 121
81
8
414
21
1
e
es
S
ep s
es
d s
d
RUR RP
QURRRRReRR R
zR
RURM ke
UR edH RR
P
FdZ FR
z
 
 


 












 




 





(10)
Using the fact that total flux is equal to the sum of the
fluxes across the two regions (peripheral and core) de-
termines the relation.
1
RR


(11)
Using the relation (10) and (11), the expression fo r the
effective (apparent) viscosity is given by:
 









22
44
22 2 4022
0
22
1
4400 42
022
12
2
12
21
1
8
414
21
1
e
es es
ep s
es
d s
d
eR R
RUR
URR R RR
R
RURM ke
UR edH RR
P
Fdz FR
z


 


 
 
 


 


 














 





 




 

 
(12)
3. Results and Discussions
To have a quantitave estimate of the various parameters
involved, particularly the hematocrit



and magnetic
field gradient
H
Hzz






, some of the results is dis-
played graphical l y in Figures 2-8.
The variation of effective viscosity

e

for differ-
ent values of magnetic field gradient

z
H
is shown in
Figure 2 and for different values of hematocrit



is
shown in Figure 3. The effective viscosity increases with
increasing value of hematocrit. Also, the effective visco-
sity increases with the increase of the magnetic field gra-
dient. The major mechanism of the influence of a static
magnetic field on blood flow viscosity is based on the
interaction between the indu ced magnetic mo ment on the
RBC and the external static magnetic field. This property
in a static magnetic field increases the friction of the
flowing blood, because the anisotropic orientation of the
RBC in the static magnetic field distribus the rolling of
the cell in flowing blood, and so the blood viscosity in-
creases [22].
Figure 4 shows the variation of flow rate ( Q) with
hematocrit of blood



for different values of mag-
netic field gradient


z
H
. It is clear from the figure that
the flow rate decreases slowly with the increase of the
(

)
Figure 2. Variation of effective viscosity


e with hema-
tocrit of blood



for different values of magnetic field
gradient



zdH dz.

R. BALI ET AL.
267

= 0.6

= 0.4

= 0.2
Figure 3. Variation of effective viscosity


e with magnetic
field gradient


zdH dz for different values hemato-
crit


.
(

)
Figure 4. Variation of blood flow rate

Q with hematocrit
of blood


for different values of magnetic field gra-
dient


zdH dz.
hematocrit and decrease with increasing values of the
magnetic field gradient. It may be observed that the flow
rate is significantly influenced by the magnetic field gra-
dient, the magnetic nature of the fluid and hematocrit of
blood



.
The variation of axial velocities profiles
f
u and
p
u
for both phase (plasma and erythrocyte) with radial axis
(r) for different values of hematocrit



are plotted in
Figures 5 and 7. It has been observed that the
f
u and
p
u decrease with increase of the hematocrit



for
constant magnetic field gradient

z
H
and other para-
meter are keep constant. The effect of hematocrit of
blood



on the velocity is relatively small near the
wall. It may be due to the red cell’s tendency to accumu-
late near the tube axis.
Figures 6 and 8, shows the variation of axial velocites
profiles
f
u and
p
u for both phase (plasma and eryt-
hrocyte) with radial axis (r) for different values of mag-
netic field gradient


z
H
. It is clear from the figure that
f
u and
p
u decrease with increase of the magnetic field
gradient. Thus, it is of importance to note that though the
suspending fluid is non magnetic the magnetic field gra-
dient influence its velo city.
All these results of the present study have been com-
pared with already existing results obtained in the theo-
retical study of [2], [13] and [21].

= 0.6

= 0.4

= 0.2
Figure 5. Variation of phase velocity

f
u with radial axis
for different values of hematocrit of blood


.

Figure 6. Vari ation of phase veloci ty


f
u with radial axis for
different values of magnetic field gradient



zdH dz.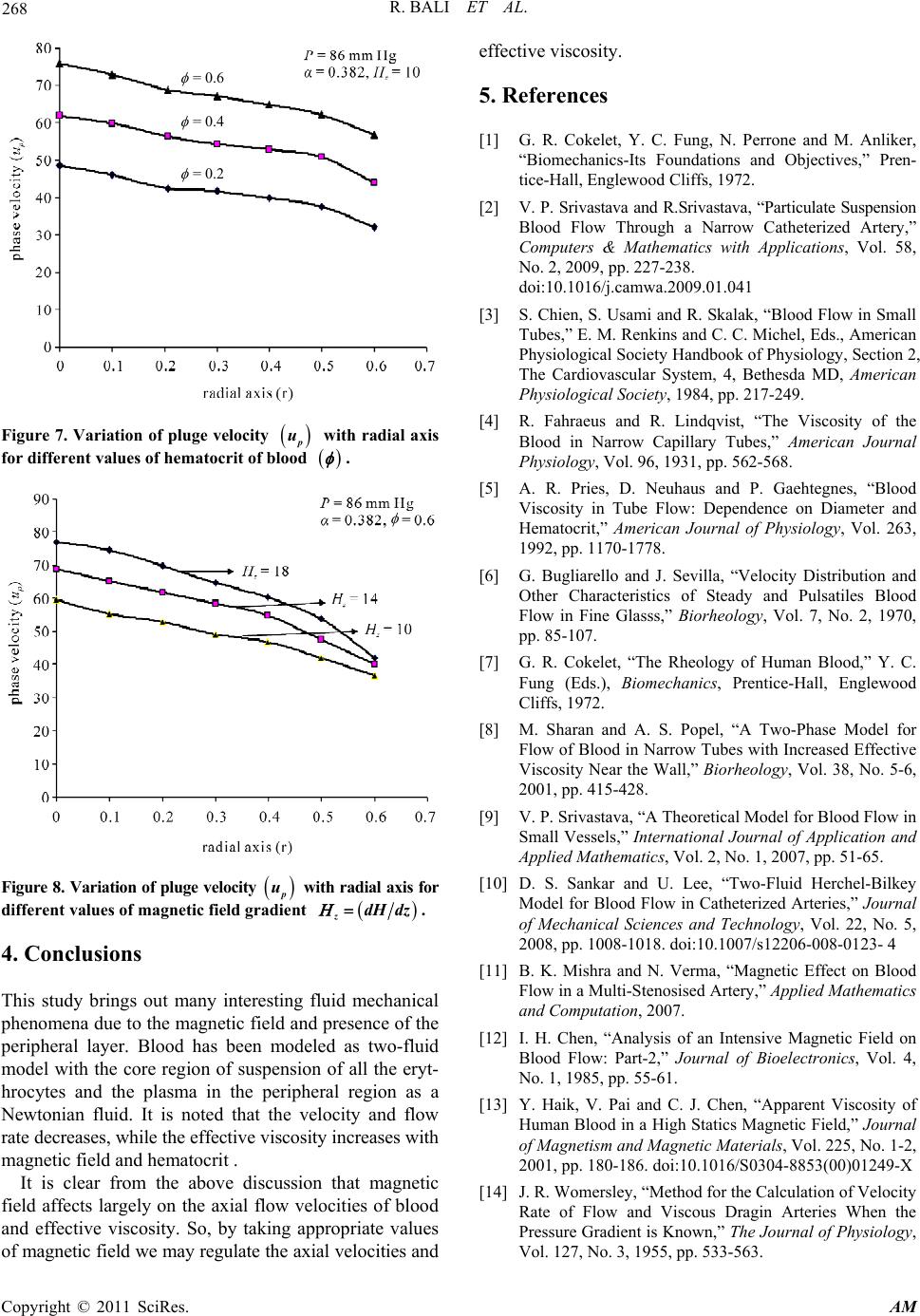

R. BALI ET AL.
268

= 0.6

= 0.4

= 0.2
Figure 7. Variation of pluge velocity

p
u with radial axis
for different values of hematocrit of blood


.

Figure 8. Variation of pluge velocity

p
u with radial axis for
different values of magnetic field gradient


zdH dz.
4. Conclusions
This study brings out many interesting fluid mechanical
phenomena due to the magnetic field and presence of the
peripheral layer. Blood has been modeled as two-fluid
model with the core region of suspension of all the eryt-
hrocytes and the plasma in the peripheral region as a
Newtonian fluid. It is noted that the velocity and flow
rate decreases, while the effective viscosity increases with
magnetic field and hematocrit .
It is clear from the above discussion that magnetic
field affects largely on the axial flow velocities of blood
and effective viscosity. So, by taking appropriate values
of magnetic field we may regulate the axial velo cities and
effective viscosity.
5. References
[1] G. R. Cokelet, Y. C. Fung, N. Perrone and M. Anliker,
“Biomechanics-Its Foundations and Objectives,” Pren-
tice-Hall, Englewood Cliffs, 1972.
[2] V. P. Srivastava and R.Srivastava, “Particulate Suspension
Blood Flow Through a Narrow Catheterized Artery,”
Computers & Mathematics with Applications, Vol. 58,
No. 2, 2009, pp. 227-238.
doi:10.1016/j.camwa.2009.01.041
[3] S. Chien, S. Usami and R. Skalak, “Blood Flow in Small
Tubes,” E. M. Renkins and C. C. Michel, Eds., American
Physiological Society Handbook of Physiology, Section 2,
The Cardiovascular System, 4, Bethesda MD, American
Physiological Society, 1984, pp. 217-249.
[4] R. Fahraeus and R. Lindqvist, “The Viscosity of the
Blood in Narrow Capillary Tubes,” American Journal
Physiology, Vol. 96, 1931, pp. 562-568.
[5] A. R. Pries, D. Neuhaus and P. Gaehtegnes, “Blood
Viscosity in Tube Flow: Dependence on Diameter and
Hematocrit,” American Journal of Physiology, Vol. 263,
1992, pp. 1170-1778.
[6] G. Bugliarello and J. Sevilla, “Velocity Distribution and
Other Characteristics of Steady and Pulsatiles Blood
Flow in Fine Glasss,” Biorheology, Vol. 7, No. 2, 1970,
pp. 85-107.
[7] G. R. Cokelet, “The Rheology of Human Blood,” Y. C.
Fung (Eds.), Biomechanics, Prentice-Hall, Englewood
Cliffs, 1972.
[8] M. Sharan and A. S. Popel, “A Two-Phase Model for
Flow of Blood in Narrow Tubes with Increased Effective
Viscosity Near the Wall,” Biorheology, Vol. 38, No. 5-6,
2001, pp. 415-428.
[9] V. P. Srivastava, “A Theoretical Model for Blood Flow in
Small Vessels,” International Journal of Application and
Applied Mathematics, Vol. 2, No. 1, 2007, pp. 51-65.
[10] D. S. Sankar and U. Lee, “Two-Fluid Herchel-Bilkey
Model for Blood Flow in Catheterized Arteries,” Journal
of Mechanical Sciences and Technology, Vol. 22, No. 5,
2008, pp. 1008-1018. doi:10.1007/s12206-008-0123- 4
[11] B. K. Mishra and N. Verma, “Magnetic Effect on Blood
Flow in a Multi-Stenosised Artery,” Applied Mathematics
and Computation, 2007.
[12] I. H. Chen, “Analysis of an Intensive Magnetic Field on
Blood Flow: Part-2,” Journal of Bioelectronics, Vol. 4,
No. 1, 1985, pp. 55-61.
[13] Y. Haik, V. Pai and C. J. Chen, “Apparent Viscosity of
Human Blood in a High Statics Magnetic Field, ” Journal
of Magnetism and Magnetic Materials, Vol. 225, No. 1-2,
2001, pp. 180-186. doi:10.1016/S0304-8853(00)01249-X
[14] J. R. Womersley, “Method for the Calculation of Velocity
Rate of Flow and Viscous Dragin Arteries When the
Pressure Gradient is Known,” The Journal of Physiology,
Vol. 127, No. 3, 1955, pp. 533-563.

R. BALI ET AL.
269
[15] E. N. Lightfoot, “Transport Phenomenon in Living Sys-
tem,” Wiley, New York, 1974.
[16] V. K. Sud and G. S. Sekhon, “Arterial Flow under Peri-
odic Body Acceleration,” Bulletin of Mathematical Bi-
ology, Vol. 47, No. 1, 1985, pp. 35-52.
[17] P. Chaturani and V. Palanisamy, “Pulsatile Flow of
Bblood with Periodic Body Acceleration,” International
Journal of Engineering Science, Vol. 29, No. 1, 1991, pp.
113-119. doi:10.1016/0020-7225(91)90081-D
[18] D. K. Wagh and S. D. Wagh, “Blood Flow Considered as
Magnetic Flow,” Proceeding of Physiology of fluid Dyna-
mics III, 1992, pp. 311-315.
[19] P. G. Saffman, “On the Stability of Laminar Flow of a
Dusty Gas,” The Journal of Fluid Mechanics, Vol. 13,
1962, pp. 120-128. doi:10.1017/S0022112062000555
[20] A. H. Nayfeh, “Osicillatory Two-Phase Flow Through a
Rigid Pipe,” AIAA Journal, Vol. 4, 1966, pp. 1868-1871.
doi:10.2514/3.3804
[21] D. C. Sanyal, K. Das and S. Debnath, “Effect of Mag-
netic Field on Pulsatile Blood Flow Through an Inclined
Circular Tube with Periodic Body Acceleration,” The
Journal of Physiological Sciences, Vol. 11, 2007, pp. 43-
56.
[22] T. Yamamoto, Y. Nagayama and M. Tamura, “A Blood-
Oxygenation Dependent Increase in Blood Viscosity Due
to a Static Magnetic Field,” Physics in Medicine and
Biology, Vol. 49, No. 14, 2004, pp. 3267-3277.
doi:10.1088/0031-9155/49/14/017