 World Journal of Condensed Matter Physics, 2013, 3, 207-215 Published Online November 2013 (http://www.scirp.org/journal/wjcmp) http://dx.doi.org/10.4236/wjcmp.2013.34035 Open Access WJCMP 207 World Journal of Condensed Matter Physics, 2013, 3, 207-215 Published Online November 2013 (http://www.scirp.org/journal/wjcmp) http://dx.doi.org/10.4236/wjcmp.2013.34035 Open Access WJCMP 207 Unimolecular Dissociation of Hydrog e n Cl u s t e r s: Measured Cross Sections and Theoretically Calculated Rate Constants + 2+1 Hn Mohamed Tabti, Adil Eddahbi, Soufiane Assouli, Lahcen El Arroum, Said Ouaskit Laboratoire Physique de la Matière Condensée (URAC10), Université Hassan II, Mohammedia, Morocco. Email: tabtimed@gmail.com Received August 23rd, 2013; revised September 26th, 2013; accepted October 17th, 2013 Copyright © 2013 Mohamed Tabti et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In this paper, we studied the process of dissociation unimolecular of the evaporation of hydrogen clusters ac- cording to size, using the Rice-Ramsperger-Kassel-Marcus (RRKM) theory. The rate constants k(E) were determined with the use of statistical theory of unimolecular reactions using various approximations. In our work, we used the prod- ucts frequencies instead of transitions frequencies in the calculation of unimolecular dissociation rates obtained by three models RRKM. The agreement between the experimental cross section ratio and calculated rate ratio with direct count approximation seems to be reasonable. 21 Hn Keywords: RRKM; Rice-Ramsperger-Kassel-Marcus; Direct Count Method; Classical Method; Whitten-Rabinovitch Method; High-Energy Cluster Collision; Fragmentation Phenomena; Cluster Fragmentation; Ionic Hydrogen Clusters; Ion-Atom Collisions; Ionic Cluster; Cross Sections; Molecular Dissociation; Size Effect; Metastable States; Hydrogen Ions 1. Introduction Unimolecular dissociation [1] is a powerful tool to probe experimentally the physical free clusters. It has been used in recent years either to measure thermodynamical prop- erties (dissociation energies [2-9] heat capacity [10]) or electronic properties (photo absorption cross-sections [11-13]). Since clusters are particles of finite size, one is con- fronted with the general question of how to detect and/or characterize such a transition in a finite system, a ques- tion of interest for many microscopic or mesoscopic sys- tems, for instance, melting and vaporization of metallic clusters, and nuclear liquid-to-gas transition [14-16]. In small systems such as two colliding nuclear or molecular systems fluctuations may wash out the signature of the phase transition [17]. Nevertheless, it has been demon- strated theoretically in Ref. [6] and also experimentally [18-20] that finite systems may indeed exhibit critical behavior to be seen when studying inclusive fragment size distributions, scaled factorial moments, and anoma- lous fractal dimensions. Protonated hydrogen clusters present the simplest ex- ample for molecular clustering and for decades has at- tracted experimental and theoretical efforts to clarify their structures and properties. The fragmentation of atomic and molecular clusters induced by energy deposition represents a fundamental interest for the physics of particle-matter or radiance- matter interactions. Experiences carried out at the IPNL (Institut de Physique Nucléaire de Lyon) demonstrated that this fragmentation is made according to several channels including evaporation, dissociation or multi- fragmentation. These different channels undergo several mechanisms according to the degree of excitation or ioni- zation or multi-ionization that reveal an individual char- acter (Rotational or vibrational excitation of the consti- tuent of the cluster) or a collective character such as the intermolecular reactivity which can explain multi-frag- mentation process. In this paper, we shall study the validity of the RRKM theory, which is based on the Assumption of the internal energy equilibration of the energized molecule and the  Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 208 and Theoretically Calculated Rate Constants dissociation rate constant of the 21 hydrogen clus- ters (n = 1, 2, 3, 4, 5) was calculated by this theory with different approximation method like: classical, Beyer- Swinehart (direct count), and Whitten-Rabinovitch (mo- dified classical). Hn 2. Protonated Hydrogen Cluster Structures The properties of protonated hydrogen clusters Hn (see Figure 1) have been studied by means of theoretical [21-31] as well as experimental methods [32-35]. In par- ticular, if n is an odd number the ab initio calculations have demonstrated that the cluster structures are basically constituted by an 3 triangular nucleus to which H2 molecules are bound. For the smaller clusters (or first- shell clusters) , 7, and 9, the H2 molecules are bound to the 3 vertices, with the H2 axes standing perpendicular to the 3 plane (the equilibrium geome- tries having C2v, C2v, and D3h symmetries, respectively). In the larger clusters, the H2 molecules are located above and below the 3 plane, and due to the weak interac- tions, the high degree of rotational freedom, at finite tem- perature, may give rise to many isomeric forms. H H H 5 H H H H Several authors have observed that the 9 is mark- edly more stable than the immediately larger cluster H 11 H [27,30,32-34] favored by a higher symmetry. In the 11 H case, the fourth H2 molecule places itself above the 3 H plane (Cs symmetry) opening a new ligand shell of H2 molecules, whose properties, like H-H distance for in- stance, are distinct from those of the internal molecules. For the 13 case, the results obtained at several theo- retical levels indicated that the two H2 molecules stand at opposite sides of the 3 plane (C2v symmetry) [26,30]. On the other hand, the results from Ref. [27] indicated that it would be energetically more advantageous if the two molecules would stay on the same side of that plane (Cs symmetry). These workers have also proposed equi- librium geometries for clusters from 15 to 35 H H HH , based on classical Monte Carlo calculations. More recently, Ignacio and Yamabe [30] presented results of ab initio calculations for clusters up to 21 , and Farizon et al. [31] performed density functional calculations (DFT) for the cluster. The results of Farizon et al. [31] for the 15 cluster are favorable to a Cs structure in which the two H2 molecules are bound one above and the other below the 3 plane. The H 27 H 15 H H H cluster has also been considered [29]. 3. Calculations and Description of the Model The Rice-Ramsperger-Kassel-Marcus theory [36-39] (RRKM) was developed by R. A. Marcus and is based on the RRK theory. The RRKM model takes into account the vibrational and rotational energies of the molecule Figure 1. Optimized structures for the clusters with n = 5 - 11. + Hn and uses the transition state concept. As in the RRK the- ory, the ergodic assumption is made and the RRKM the- ory can also be described as a micro canonical transition state theory. In this theory AB is identified as the transition state of the reaction. A transition state is defined as the “dividing surface” between reactants and products, and its location is determined by the condition that every trajectory (flux), which passes this surface, will form the products without recrossing. There are several ways to calculate sums and densities like: 3.1. Direct Count Method Beyer and Swinehart (BS) have introduced an extremely efficient, simple, and accurate algorithm [40] which ap- plies to harmonic molecular models. If an energy step is chosen which divides exactly the normal frequencies of the model, the BS algorithm allows the calculation of these functions by “directly counting” all states. The re- sults are therefore exact within the framework of the given theory that determines the states. The sum of states N(E) can be obtained either by di- rect numerical integration of the density of states or computed directly by using the Beyer-Swineherd of states N(E). The program calculates N(E) by dividing the energy scale into a series of cells and counting how many vibrational bands are in each cell. The algorithm goes through with the lowest frequency and puts a 1 in each cell where the frequency or its overtone arises. It then goes through with the second frequency and adds one to the cell if the cell is an overtone, or if some combination of the previous frequencies are in the cell. The effect is a complete count of the number of frequencies contributing to the cell. Open Access WJCMP  Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 209 and Theoretically Calculated Rate Constants If a system consists of s harmonic oscillators with fre- quencies of i = νi/c cm−1, where c is the speed of light, each will have a series of equally spaced states located at Ei = Ni i (Ni = 0, 1, 2···). The zero of energy is the ion’s zero point energy and the internal energy is divided into bins of size 1 cm−1. The direct count of the number of vibrational states of 21 , up to a total energy of value of energy activation E0, is split into two tables; in the first one, energies of the lower vibrational states are calculated; in the second, the number of quantum states of is calculated. Hn 21 The formula giving the energies is: Hn 1 11 cm,1,2, 3 s ij i ij Envn (1) The direct count of the number of states gives rise to combinatorial problem for the counting of degenerate states. The number of ways to accommodate n quanta in q oscillators is given by: 1! !1! nq wE nq (2) A simple program can calculate these functions. Al- though the required programming is very simple, it does have several draw-backs. First, it is the most time con- suming approach, which becomes a problem when deal- ing with large ions. Second, in most calculations one is interested in the density or sum of states at a few energies that are well above the minimum energy for dissociation. However, in the exact count method one is obliged to calculate these functions from 0 up to the maximum en- ergy of interest. Third, each frequency is treated sepa- rately so that frequencies cannot be bunched to save time in calculations. For these reasons, it is generally worth- while to invest the additional programming time required for the following two approximate methods. A description of the original BS algorithm in [40], the original BS algorithm treats all the vibrations separately regardless of degeneracy. It is obvious that reduction in computation time may occur if a method to treat degen- erate vibrations all at the same time can be devised. In the grouped-frequency direct counting mode of RRKM calculation used before the advent of the BS algorithm, this was achieved by taking advantage of the fact that the number of ways to distribute j vibrational quanta into g degenerate 3.2. Classical Method The classical mechanical RRKM k(E) takes a very sim- ple form, if the internal degrees of freedom for the reac- tant and transition state are assumed to be harmonic os- cillators. The classical sum of states for s harmonic os- cillators is [41]. The most general expression for the RRKM reaction rate constant is given by: # GE kE hN E (3) where G#(E) represents the sum of states for the active degrees of freedom in the transition state and N(E) de- notes the density of states for the active degrees of free- dom in the reactant. For the calculation of the RRKM reaction rate constant, the classical expressions for the sum and density of states can be used: # 1 ! s s i i E GE h (4) where s represents the number of oscillators, E denotes the energy of the activated complex and νi is frequency of the oscillator i. The density N(E) = dG#(E)/dE is then 1 1 E 1! s s i i E N h . (5) The reactant density of states in Equation (2) is given by the above expression for N(E). The sum of the transi- tion state is 1 0 # 01# 1 1! s s i i EE GEE h (6) Inserting Equation (5) and Equation (6) into Equation (3) gives 1 10 1# 1 s i i s i i EE kE E (7) 3.3. Whitt en- Rabi novitc h Method The Whitten-Rabinovitch [42] method is based on the classical sum of states calculation. The equation for cal- culating the sum of states is 1 0 # 01# 1 1! s z s i i EE E GEE sh (8) where E is the energy, E0 is the activation energy, h is Planck’s constant, νi are the vibrational frequencies, s is the number of frequencies, and α is a constant which varies from 0 to 1 as the energy goes from 0 to infinity. The parameter α, β, and w are empirically set to approxi- mate the exact quantum mechanical count. They are 0.25 1 0.5 2 2 1 log1.0506E, for 5.00E2.73E3.51, 1 for , zz zz z EEE EE s EE s (9) Open Access WJCMP 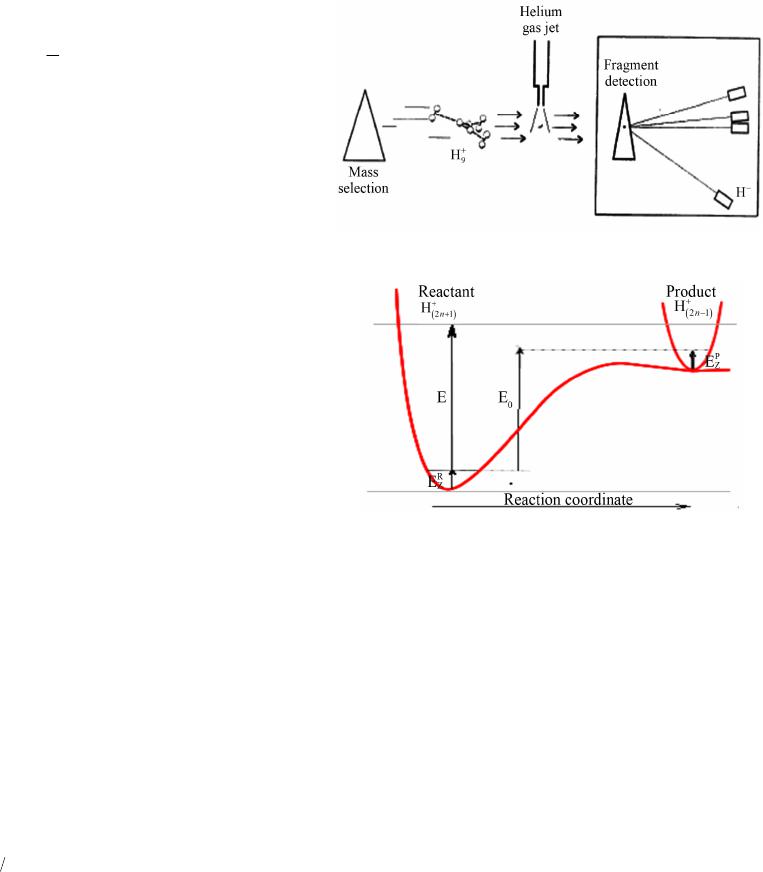 Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 210 and Theoretically Calculated Rate Constants and EZ is the zero point energy given by: 1 1 2 s i i Eh (10) 4. Experimental Approach Mass selected hydrogen cluster ions with an energy of 60 keV/amu are prepared in a high-energy cluster ion beam facility consisting of a cryogenic cluster jet expansion source combined with a high performance electron ion- izer and a two-step ion accelerator (consisting of an elec- trostatic field and a RFQ post-accelerator). In the present study, the beam of mass selected m cluster ions (m = l, 14) is crossed perpen- dicularly by a helium target beam effusing from a cylin- drical capillary tube. The undissociated primary 32 HH 32 HH m cluster projectile ion or the neutral and charged fragments resulting from reactive collisions, are then passing a magnetic sector field analyzer and detected with a multi detector device consisting of an array of passivated im- planted planar silicon surface barrier detectors located at different positions at the exit of the magnetic analyzer With this instrument we are able to record for each event simultaneously the number of each mass-identified frag- ment ion resulting from the interaction (for more expe- rimental details, see [19,20,43]). Thus this experimental approach is able to analyze on an event-by-event basis the identity of all correlated fragments produced in a single collision event between the cluster ion and the He target atom, the fragmentation reactions having the general form. 32 HH m 323232 2 HHHHH HH +eH, with0,1 mk eab c d fHa f (11) Several processes of fragmentation of clusters ionized hydrogen 32 HH 32 2 n (n = 5 - 35 see Equation (13)) were studied by S.Louc and M. Farizon et al. [44-48] using the same experimental situation (see Figure 2): the fragmentation of the clusters is induced by collision with a helium atom at high speed (60 keV/u). Measurements of the total destruction cross sections SIGMA of the hydrogen clusters m with 0 ≤ m ≤ 16 were done by S. Louc with the size of the cluster and reported in the first row in Table 1. 32 HH 32 32 1 HHHe > HHH mm (12) 5. RRKM Calculations Results The dissociation of 21 occurs if the energy of vibra- tion along the reaction coordinate exceeds the activation energy, i.e., the barrier height (or the heat of reaction, if the reaction does not have a distinct transition state, see Figure 3). The probability of this event can be calculated Hn Figure 2. Experimental set-up. Figure 3. Reaction coordinate for a dissociation with a very low barrier. The active energy E is measured from the zero point energy of the reactant well. The critical energy E0 is the zero point energy difference between the product well and the reactant well. using the statistical approach of the RRKM theory. For the parent 21 Hn ion, the available internal energy is the part of the excitation energy beyond the ionization threshold, which is converted to vibration energy. After dissociation, the internal energy of secondary fragments is less than the energy of the parent molecule, because of the fact that the excess energy is distributed among the product species and can be approximated as being pro- portional to the ratio of internal degrees of freedom of the fragment and the parent molecule. The reaction coordinate should be excluded from the total numbers of internal degrees of freedom, because the kinetic energy along the reaction coordinate is supposed to be close to the barrier’s height and is already subtracted from the total internal energy. Because the reaction occurs via transition state, the initiating energy for this reaction is the barrier’s height at TS. The energy difference between the barrier’s and the energy of products is converted to kinetic energies of the fragments. In our work we neglect the energy difference between the barrier’s and the energy of products then the available internal energy of the H2. Because the assumption that the energy difference between the barrier’s and the en- ergy of products is converted to the kinetic energies of he fragments is very crude, and energy difference be- t Open Access WJCMP 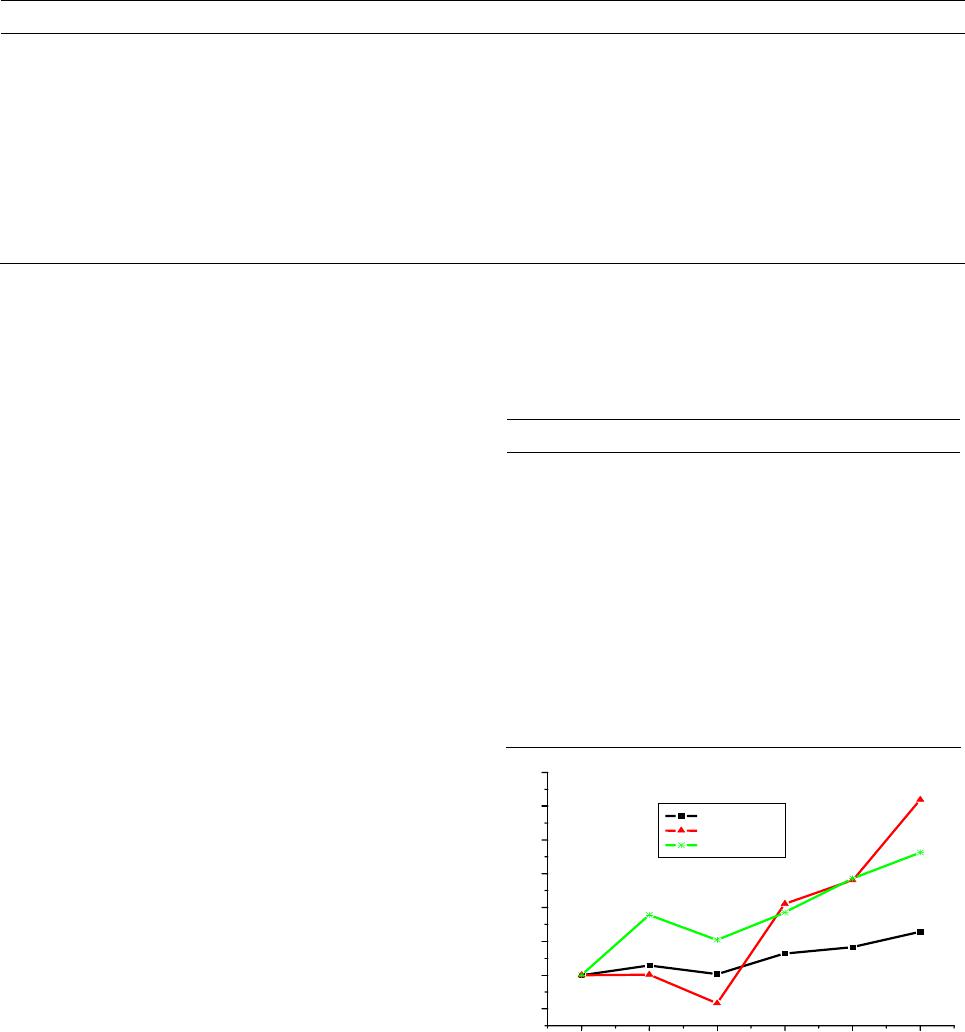 Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections and Theoretically Calculated Rate Constants Open Access WJCMP 211 Table 1. Comparison of dissociation unimolecular rates for H2 atom loss predicted by three Models (Classical, BS and the WR ) at E = 8 kcal/mol excitation energy. + 3 H + 5 H + 7 H + 9 H + 11 H + 13 H SIGMA 0.36 0.46 0.37 0.59 0.66 0.82 Rate Eun J BS 4.17E+10 4.23E+10 6.79E+09 1.30E+11 1.59E+11 2.58E+11 Rate Eun J WR 1.11E+10 4.28E+10 9.04E+09 3.11E+11 1.46E+12 3.26E+11 Rate Eun J CL 2.17E+11 1.82E+12 6.24E+11 5.67E+13 1.94E+13 3.55E+14 Rate Rita BS 1.36E+10 3.77E+10 2.76E+10 3.86E+10 5.23E+10 6.27E+10 Rate Rita WR 8.20E+09 3.28E+10 2.98E+10 3.59E+10 1.20E+11 1.02E+11 Rate Rita CL 4.33E+10 4.04E+12 2.29E+12 1.41E+12 1.94E+13 2.26E+13 tween the initiation energies of the 21 and 21 Hn Hn dissociation is small, in other words, The internal energy value of E = E0 is sufficient to initiate the 21 Hn ion dissociation, which is sufficient for the H2 loss reaction to occur. The H2 elimination reaction passes through transition state TS with a low barrier of value E = E0 and produces the ion. Table 2. The ratio of rate constant of unimolecular dissocia- tion (kdiss []/kdiss []) obtained by Classical, BS and the WR Methods for Rita and Hireoka and Eun-Jung In and the ratio of cross sections of unimolecular dissociation ( [/ []) that found experimentally . + n H + 5 H + 5 H + n H] + 3 H+ 5 H+ 7 H + 9 H + 11 H+ 13 H Ratio of SIGMA1.001.281.03 1.64 1.832.28 Ratio of Rate EunJ BS 1.001.010.16 3.11 3.816.19 Ratio of Rate EunJ WR 1.003.85 0.81 27.98 131.4729.35 Ratio of Rate EunJ CL 1.008.382.88 261.32 89.581635.32 Ratio of Rate Rita BS 1.002.782.04 2.85 3.864.63 Ratio of Rate Rita WR 1.004.003.63 4.38 14.6812.44 Ratio of Rate Rita CL 1.0093.3952.92 32.65 448.09523.24 21 In our work, we consider that the active energy E is measured from the zero-point energy of the reactant well. The critical energy E0 is the difference between the zero- point energy and the product and the reactant well. Hn The originality of our work is the use of products fre- quencies instead of frequencies of transitions to calculate the unimolecular dissociation rate according to three models of RRKM, i.e. we calculate the rate constant us- ing: 1) The dissociation energies E0 published in [31] by farizon, and the fundamental frequencies of vibration of parent 21 and vibrational frequencies of product published in [49] by Eun-Jung In. Hn 21 2) The dissociation energies E0 published by Hireoka in [50-52] and the fundamental frequencies of vibration of parent 21 and vibrational frequencies of product published in [53] by Rita. Hn + 5 H+ 7 H+ 9 H+ 11 H + 13 H + 15 H 0 1 2 3 4 5 6 Cluster Size RatioSIGMA RatioEunJBS RatioRitaBS RATIO Hn 21 First we launched our simulation program by varying the excitation energies between 5.7 and 9 kcal/mol. Hn For hydrogen ion aggregates, at E = 8 kcal/mol, we present in Table 1 the results calculations of the uni- molecular rate constant K(E) obtained by three models with values of (Rita and Hireoka) and Eun-Jung In are compared with each other, with experimental results of cross sections of dissociation. Then we shall Use The ratio k(E)/k(E) min of the RRKM unimolecular rate constant, which will be com- pared with The ratio diss/ dissmin of cross sections previously measured (see Table 2). Figure 4. Comparison of the ratio of evaporation rates con- stant for the Direct count Method or Beyer and Swinehart (BS) model according to the RRKM theory of clusters + 21 Hn following the loss of a neutral H2 molecule with the cross section of unimolecular dissociation that found ex- perimentally. Then we draw in Figure 4 both the curves of the ratio of cross sections of unimolecular dissociation that found experimentally and the ratio of evaporation rates constant 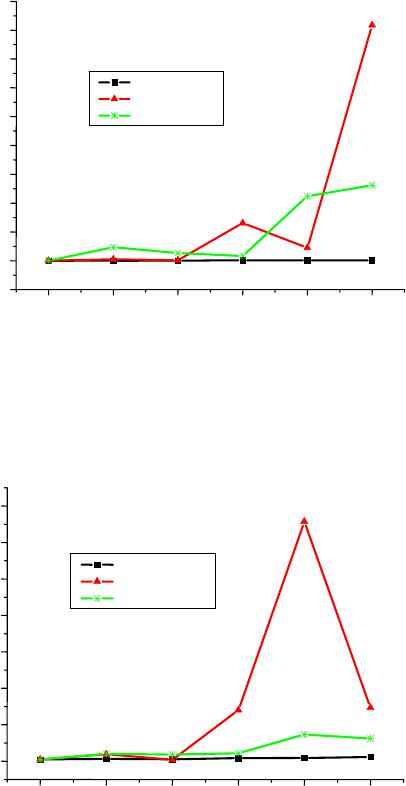 Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 212 and Theoretically Calculated Rate Constants calculated using different models of RKKM. In this figure, we note that both theoretical curves for the ratio of rate dissociation rates present the same shape as the curve with the experimental results relative to cross sections; we also note the presence of two parts, In the first part, clusters of zone 9 H, 7 H and 5 H where these three aggregates report rate dissociation of Eun-Jung In are slightly lower than those of RITA and Hireoka due to the fact that the values of dissociation energies E0 of Rita and Hireoka are higher than those of Eun-Jung In; In the second part where are the unimolecular disso- ciation of clusters 11 H, 13 H and 15 H, the two theo- retical curves for the ratio of dissociation rates have the same shape as the curve with the experimental results the reports of cross sections, but they have differences which are due to low values of the energy of dissociation from the high excitation energy given to the aggregate and that the values of the ratios of rates are slightly higher compared to the experimental factor 3, while those of Eun-Jung In are slightly ele- vated with a factor 5. The theoretical curves show that the evaporation rate using fundamental frequencies follows the same varia- tions as the cross section for dissociation values (n = 5, 7, 9, 11, 13, 15) and The two curves are indistinguishable except for the aggregate 11 and 15 a slight shift is observed. But there is a wide gap curves for the aggregate . HH 13 In both Figures 5 and 6 we note the presence of two parts: H In the first one, concerning the unimolecular dissocia- tion of the clusters 9 H, 7 H and 5 H we note how these three aggregates report rate dissociation of Eun- Jung In are slightly lower than those of Rita and Hir- eoka due to the fact that the values of dissociation en- ergies E0 of Rita and Hireoka are higher than those of Eun-Jung In, but in this part, the evaporation rates are slightly lower than those of Rita and Hireoka because the values of the dissociation energies E0 of Rita and Hireoka are slightly higher than those of Eun-Jung In. In the second part, the two theoretical curves for the ratio of the dissociation rate on unimolecular disso- ciation of clusters 11 H, 13 H and 15 H have the same shape as the curve related to the experimental results of cross sections, but they have differences which are due to lower values of the dissociation energies rela- tive to the excitation energy E given to the aggregate to dissociate, and the fact that both the two formulas are empirical. 6. Discussion A comparison of methods for calculating the ratio of rates + 5 H+ 7 H+ 9 H + 11 H + 13 H+ 15 H -200 0 200 400 600 800 1000 1200 1400 1600 1800 RATIO Cluster Size Rati oS IGM A RatioEunJCL RatioRitaCL Figure 5. Comparison of the ratio of evaporation rates con- stant for the classical model according to the RRKM theory of clusters following the loss of a neutral H2 mole- cule with the cross section of unimolecular dissociation that found experimentally. + 2+1 Hn + 5 H+ 7 H+ 9 H + 11 H + 13 H+ 15 H 0 20 40 60 80 100 120 Cluster Size Rat ioSIG MA RatioEunJWR RatioRitaWR 140 RATIO Figure 6. Comparison of the ratio of evaporation rates con- stant for the Semi classical or Whitten-Rabinovitch (WR) model according to the RRKM theory of clusters following the loss of a neutral H2 molecule with the cross section of unimolecular dissociation that found experimen- tally. + 2+1 Hn constant for 21 Hn clusters following the loss of a neutral H2 molecule, it will be shown that the results of the uni- molecular dissociation obtained from RRKM theory with the three models: Classical (CL), Beyer-Swinehart (BS), and Whitten-Rabinovitch (WR). Using the vibrational frequencies of products are better, than that from the ex- perimental data. The curves obtained by the three modes, particularly that of the method (BS) have the same shape as that of the curved cross-section which shows the results obtained experimentally. Open Access WJCMP  Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 213 and Theoretically Calculated Rate Constants To assess and compare the rate of unimolecular disso- ciation of clusters , we have provided a value of ex- citing energy E (E = 8 kcal/mol) greater than all the values of the dissociation energies E0 of all clusters, we see that all the theoretical curves for the three approximations have qualitatively the same shape as the curve of the ratio of the cross section, whereas aggregates 13 and 15 Hn HH only the theoretical curves based on direct calculation (BS) that keeps the same pace as experimental, but other like approximations classical (CL) or semi-classical (WR) where the calculation of rate constant is based on em- pirical formulas and where the values of the dissociation energies E0 of clusters are very small compared to the exciting energy E, it gives some errors on the values of the dissociation rate. 7. Conclusions In this paper we have presented different way of calcu- lating rate constant of unimolecular dissociation of clus- ters with RKKM model. This model takes into account the frequencies of products instead of the frequencies of transition state. We conclude that the comparison between the normal- ized unimolecular dissociation cross sections obtained experimental and normalized rates constants calculated using different models, showing that the RRKM model is qualitatively consistent with the experimental data. Generally in the three methods exposed in this work, we note that Rates constants calculated by using input parameters according to Rita and Hireoka (high dis- sociation energies) are too high for those reported by Eun-Jung In (low dissociation energies). The curves obtained by the three methods especially that of the Beyer-Swinehart method present the same shape as that of the cross section curve obtained ex- perimentally. In addition we observe that Beyer-Swine- hart is a good approximation method in analyzing the experimental data of unimolecular reactions. The curves of the other models (WR) and (CL) have almost the same shape as the experimental curve but quantitatively the normalized rates constants are far from the normalized cross sections. RRKM model can serve as theoretical base of inter- pretations of the dissociation of internally excited mo- lecular ions, either in thermal collision in gas or for experience of collision inducing dissociation. The validity of the RRKM based on direct count me- thod or Beyer-Swinehart. Using the frequencies of vibra- tion of the products instead of vibration frequencies of the transition complex is entirely acceptable with regard to the behavior of the rate constant as a function of the ex- citation energy. REFERENCES [1] W. Forst, “Theory of Unimolecular Reactions,” Aca- demic Press, New York, 1973. [2] S. Wei, B. Tzeng and A. W. Castleman Jr., “Kinetic En- ergy Release Measurements of Ammonia Cluster Ions during Metastable Decomposition and Determination of Cluster Ion Binding Energies,” Journal of Chemical Physics, Vol. 92, No. 1, 1990, p. 332. http://dx.doi.org/10.1063/1.458434 [3] C. Bréchignac, Ph. Cahuzac, J. Leygnier and J. Weiner, “Dynamics of Unimolecular Dissociation of Sodium Cluster Ions,” Journal of Chemical Physics, Vol. 90, No. 3, 1989, p. 1492. http://dx.doi.org/10.1063/1.456675 [4] C. Bréchignac, H. Bush, Ph. Cahuzac and J. Leygnier, “Dissociation Pathways and Binding Energies of Lithium Clusters from Evaporation Experiments,” Journal of Che- mical Physics, Vol. 101, No. 8, 1994, p. 6992. http://dx.doi.org/10.1063/1.468326 [5] C. X. Su, D. A. Hales and P. B. Armentrout, “Collision Induced Dissociation of Vn (n = 2 - 20) with Xe: Bond Energies, Dissociation Pathways, and Structures,” Jour- nal of Chemical Physics, Vol. 99, No. 9, 1993, p. 6613. http://dx.doi.org/10.1063/1.465853 [6] U. Hild, G. Dietrich, S. Krückeberg, M. Lindinger, K. Lützenkirchen, L. Schweikhard, C. Walther and J. Siegler, “Time-Resolved Photofragmentation of Stored Silver Clusters Agn (n = 8 - 21),” Physical Review A, Vol. 57, No. 4, 1998, pp. 2786-2793. http://dx.doi.org/10.1103/PhysRevA.57.2786 [7] U. Ray, M. F. Jarrold, J. E. Bower and J. S. Kraus, “Pho- todissociation Kinetics of Aluminum Cluster Ions: De- termination of Cluster Dissociation Energies,” Journal of Chemical Physics, Vol. 91, No. 5, 1989, pp. 2912-2921. http://dx.doi.org/10.1063/1.456961 [8] H. J. H wang, D. K. Sensharma and M. A. El Sayed, “Size and Temporal Dependence of the Average Kinetic- Energy Release during the Evaporation of Sputtered CsCsI n Clusters,” Physical Review Letters, Vol. 64, No. 7, 1990, pp. 808-811. http://dx.doi.org/10.1103/PhysRevLett.64.808 [9] J. A. Smith, N. G. Grotts, J. F. Winkel, R. Hallett, A. J. Stace and B. J. Whitaker, “The Decay Dynamics of Pho- toexcited Argon Cluster Ions,” Journal of Chemical Phy- sics, Vol. 97, No. 1, 1992, p. 397. http://dx.doi.org/10.1063/1.463584 [10] M. Schmidt, R. Kusche, W. Kronmuller, B. Von Issen- dorff and H. Haberland, “Experimental Determination of the Melting Point and Heat Capacity for a Free Cluster of 139 Sodium Atoms,” Physical Review Letters, Vol. 79, No. 1, 1997, pp. 99-102. http://dx.doi.org/10.1103/PhysRevLett.79.99 [11] W. de Herr, K. Selby, V. Kresin, J. Masui, M. Vollmer, A. Chatelain and W. D. Knight, “Collective Dipole Oscilla- tions in Small Sodium Clusters,” Physical Review Letters, Vol. 59, No. 16, 1987, pp. 1805-1808. http://dx.doi.org/10.1103/PhysRevLett.59.1805 Open Access WJCMP  Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections 214 and Theoretically Calculated Rate Constants [12] C. Bréchignac, Ph. Cahuzac, F. Carlier and J. Leygnier, “Collective Excitation in Closed-Shell Potassium Cluster Ions,” Chemical Physics Letters, Vol. 164, No. 4, 1989, pp. 433-437. http://dx.doi.org/10.1016/0009-2614(89)85233-9 [13] C. Bréchignac, Ph. Cahuzac, N. Kébaili, J. Leygnier and A. Serfati, “Collective Resonance in Large Free Potas- sium Cluster Ions,” Physical Review Letters, Vol. 68, No. 26, 1992, pp. 3916-3919. http://dx.doi.org/10.1103/PhysRevLett.68.3916 [14] F. Gulminelli and P. Chomaz, “Critical Behavior in the Coexistence Region of Finite Systems,” Physical Review Letters, Vol. 82, No. 7, 1999, pp. 1402-1405. http://dx.doi.org/10.1103/PhysRevLett.82.1402 [15] M. D’Agostino, M. Bruno, F. Gulminelli, F. Cannata, Ph. Chomaz, G. Casini, E. Geraci, F. Gramegna, A. Moroni and G. Vannini, “Nuclear Liquid-Gas Phase Transition: Experimental Signals,” Nuclear Physics A, Vol. 749, 2005, pp. 55c-64c. http://dx.doi.org/10.1016/j.nuclphysa.2004.12.008 [16] P. Chomaz and F. Gulminelli, “The Challenges of Finite- System Statistical Mechanics,” The European Physical Journal A, Vol. 30, No. 1, 2006, pp. 317-331. http://dx.doi.org/10.1140/epja/i2006-10126-5 [17] A. Bonasera, M. Brano, C. O. Dorso and P. F. Mastinu, “Critical Phenomena in Nuclear Fragmentation,” Rivista Del Nuovo Cimento, Vol. 23, No. 2, 2000, pp. 1-102. [18] M. Belkacem, V. Latora and A. Bonasera, “Critical Evo- lution of a Finite System,” Physical Review C, Vol. 52, No. 1, 1995, pp. 271-285. http://dx.doi.org/10.1103/PhysRevC.52.271 [19] B. Farizon, M. Farizon, M. J. Gaillard, F. Gobet, M. Carré, J. P. Buchet, P. Scheier and T. D. Märk, “Experi- mental Evidence of Critical Behavior in Cluster Frag- mentation Using an Event-by-Event Data Analysis,” Phy- sical Review Letters, Vol. 81, No. 19, 1998, pp. 4108- 4111. http://dx.doi.org/10.1103/PhysRevLett.81.4108 [20] B. Farizon, M. Farizon, M. J. Gaillard, R. Genre, S. Louc, J. Martin, J. P. Buchet, M. Carré, G. Senn, P. Scheier and T. D. Märk, “Mass Distribution and Multiple Fragmenta- tion Events in High Energy Cluster—Cluster Collisions: Evidence for a Predicted Phase Transition,” International Journal of Mass Spectrometry and Ion Processes, Vol. 164, No. 3, 1997, pp. 225-230. http://dx.doi.org/10.1016/S0168-1176(97)00091-8 [21] S. Yamabe, K. Hirao and K. Kitaura, “Theoretical Study on the Stability and the Structure,” Chemical Physics Letters, Vol. 56, No. 3, 1978, pp. 546-548. http://dx.doi.org/10.1016/0009-2614(78)89036-8 [22] H. Huber, “Geometry Optimization in ab Initio SCF Cal- culations III. Floating Orbital Geometry Optimization (FOGO) with Floating Outer Shell Basis Functions,” Chemical Physics Letters, Vol. 70, 1980, p. 353. http://dx.doi.org/10.1016/0009-2614(80)85349-8 [23] L. R. Wright and R. F. Borkman, “Ab Initio Studies on the Stabilities of Even- and Odd-Membered Hn Clus- ters,” Journal of Chemical Physics, Vol. 77, No. 4, 1982, p. 1938. http://dx.doi.org/10.1063/1.444047 [24] Y. Yamaguchi, J. F. Gaw and H. F. Schaefer III, “Mo- lecular Clustering about a Positive Ion. Structures, Ener- getics, and Vibrational Frequencies of the Protonated Hydrogen Clusters 3 H , 5 H, 7 H, and 9 H,” Journal of Chemical Physics, Vol. 78, No. 6, 1983, p. 4074. http://dx.doi.org/10.1063/1.445135 [25] M. Farizon, B. Farizon-Mazuy, N. V. de Castro Faria and H. Chermette, “Ab Initio Structure Calculations of Hy- drogen Ionic Clusters,” Chemical Physics Letters, Vol. 177, No. 4-5, 1991, pp. 451-457. http://dx.doi.org/10.1016/0009-2614(91)85082-8 [26] M. Farizon, H. Chermette and B. Farizon-Mazuy, “Struc- ture and Energetics of Hydrogen Clusters. Structures of 11 H and 13 H . Vibrational Frequencies and Infrared In- tensities of the 21 Hn Clusters (n = 2 - 6),” Journal of Chemical Physics, Vol. 96, No. 2, 1992, p. 1325. http://dx.doi.org/10.1063/1.462168 [27] U. Nagashima, K. Morokuma and H. Tanaka, “Ab Initio and Monte Carlo Study of the Structure and Stability of Hydrogen Clusters 32 HH n (n = 3 - 16),” Journal of Physical Chemistry, Vol. 96, No. 11, 1992, pp. 4294- 4300. http://dx.doi.org/10.1021/j100190a036 [28] T. Pang, “Properties of Ionic Hydrogen Clusters: A Quan- tum Monte Carlo Study,” Chemical Physics Letters, Vol. 228, No. 6, 1994, pp. 555-561. http://dx.doi.org/10.1016/0009-2614(94)01000-5 [29] I. Stich, D. Marx, M. Parrinelo and K. Terakura, “Proton- Induced Plasticity in Hydrogen Clusters,” Physical Re- view Letters, Vol. 78, No. 19, 1997, pp. 3669-3672. http://dx.doi.org/10.1103/PhysRevLett.78.3669 [30] E. W. Ignacio and S. Yamabe, “A Symmetric Structure of the Gas-Phase 32 9 HH Cluster,” Chemical Physics Letters, Vol. 287, No. 5-6, 1998, pp. 563-569. http://dx.doi.org/10.1016/S0009-2614(98)00237-1 [31] B. Farizon, M. Farizon, H. Razafinjanahary and H. Cher- mette, “Structure and Energetics of 15 H Hydrogen Clus- ters,” Physical Review B, Vol. 60, No. 6, 1999, pp. 3821- 3828. http://dx.doi.org/10.1103/PhysRevB.60.3821 [32] A. van Lumig and J. Reuss, “Collisions of Hydrogen Cluster Ions with a Gas Target, at 200 - 850 eV Energy,” International Journal of Mass Spectrometry and Ion Phy- sics, Vol. 27, No. 2, 1978, pp. 197-208. http://dx.doi.org/10.1016/0020-7381(78)80039-4 [33] M. Okumura, L. I. Yeh and Y. T. Lee, “Infrared Spec- troscopy of the Cluster Ions 32 HH n ,” Journal of Che- mical Physics, Vol. 88, No. 1, 1988, p. 79. http://dx.doi.org/10.1063/1.454488 [34] K. Hiraoka and T. Mori, “Thermochemical Stabilities of 33 DD n with n = 1 - 10,” Chemical Physics Letters, Vol. 157, No. 5, 1989, pp. 467-471. http://dx.doi.org/10.1016/0009-2614(89)87282-3 [35] S. Louc, B. Farizon, M. Farizon, M. J. Gaillard, N. Gon- Open Access WJCMP  Unimolecular Dissociation of 21 Hn Hydrogen Clusters: Measured Cross Sections and Theoretically Calculated Rate Constants Open Access WJCMP 215 [46] B. Farizon, M. Farizon, M. J. Gaillard, F. Gobet, C. Guil- lermier, M. Carré, J. P. Buchet, P. Scheier and T. D. Märk, “Universal Behaviour in Fragmentation Phenomena? The Cluster Case,” European Physical Journal D, Vol. 5, No. 1, 1999, pp. 5-8. http://dx.doi.org/10.1007/s100530050222 çalves, H. Luna, G. Jalbert, N. V. de Castro Faria, M. C. Bacchus-Montabonel, J. P. Buchet and M. Carré, “Elec- tron Capture in the Collision of Mass-Selected Hydrogen- Cluster Ions with Helium Atoms,” Physical Review A, Vol. 58, No. 5, 1998, pp. 3802-3806. http://dx.doi.org/10.1103/PhysRevA.58.3802 [36] O. K. Rice and H. C. Ramsperger, “Theories of Unimo- lecular Gas Reactions at Low Pressures. II,” Journal of the American Chemical Society, Vol. 50, No. 3, 1928, pp. 617-620. http://dx.doi.org/10.1021/ja01390a002 [47] B. Farizon, M. Farizon, M. J. Gaillard, F. Gobet, J. P. Buchet, M. Carre, P. Scheier and T. D. Märk, “Cooling and Heating of Channeled Ions and Corresponding Char- ge State Distributions,” Nuclear Instruments and Methods in Physics Research Section B, Vol. 209, 2003, pp. 9-18. http://dx.doi.org/10.1016/S0168-583X(02)02011-6 [37] L. S. Kassel, “Kinetics of Homogeneous Gas Reactions,” Chemical Catalog Co., New York, 1932. [48] S. Eden, J. Tabet, K. Samraoui, S. Louc, B. Farizon, M. Farizon, S. Ouaskit and T. D. Märk, “Absolute Cross Sections for the Dissociation of Hydrogen Cluster Ions in High-Energy Collisions with Helium Atoms,” Physical Review A, Vol. 73, No. 2, 2006, Article ID: 023201. http://dx.doi.org/10.1103/PhysRevA.73.023201 [38] R. A. Marcus and O. K. Rice, “The Kinetics of the Re- combination of Methyl Radicals and Iodine Atoms,” Journal of Physical and Colloid Chemistry, Vol. 55, No. 6, 1951, pp. 894-908. http://dx.doi.org/10.1021/j150489a013 [39] T. Beyer and D. F. Swinehart, Comm. Ass. Com. Mach, Vol. 16, 1973, p. 379. [49] E.-J. In, H.-I. Seo and S.-J. Kim, “The ab Initio Quantum Mechanical Investigation for the Weakly Bound 21 Hn (n = 1 - 6) Complexes,” Journal of the Korean Chemical Society, Vol. 45, No. 5, 2001. [40] P. J. Robinson and K. A. Holbrook, “Unimolecular Reac- tions,” Wiley-Interscience, New York, 1972. [41] T. Baer and P. M. Mayer, “Statistical Rice-Ramsperger- Kassel-Marcus Quasiequilibrium Theory Calculations in Mass Spectrometry,” Journal of the American Society for Mass Spectrometry, Vol. 8, No. 2, 1997, pp. 103-115. http://dx.doi.org/10.1016/S1044-0305(96)00212-7 [50] K. Hiraoka and P. Kebarle, “A Determination of the Sta- bilities of 5 H , 7 H , 9 H , and 11 H from Measurement of the Gas Phase Ion Equilibria 22n HHH n (n = 3, 5, 7, 9),” Journal of Chemical Physics, Vol. 62, No. 6, 1975, p. 2267. http://dx.doi.org/10.1063/1.430751 [42] G. Z. Whitten and B. S. Rabinovitch, “Approximation for Rotation—Vibration Energy Level Sums,” Journal of Chemical Physics, Vol. 41, No. 6, 1964, p. 1883. http://dx.doi.org/10.1063/1.1726175 [51] K. Hiraoka, “A Determination of the Stabilities of 32 HH n with n = 1-9 from Measurements of the Gas-Phase ion Equilibria 322 32 1 HHH HH nn ,” Journal of Chemical Physics, Vol. 87, 1987, p. 4048. [43] M. E. Fisher, “The Theory of Equilibrium Critical Phe- nomena,” Reports on Progress in Physics, Vol. 30, 1967, p. 615. http://dx.doi.org/10.1088/0034-4885/30/2/306 [52] K. Hiraoka and T. Mori, “Thermochemical Stabilities of 33 DD n with n = 1 - 10,” Chemical Physics Letters, Vol. 157, No. 5, 1989, pp. 467-471. http://dx.doi.org/10.1016/0009-2614(89)87282-3 [44] S. Louc, “Mesure des Sections Efficaces des Différents Processus Intervenant dans la Fragmentation d’Agrégats d’Hydrogène Hn (3 ≤ n ≤ 35) Induite par Collision à Haute Vitesse (60 keV/u) sur un Atome d’Hélium (60 keV/u) avec un Atome d’Hélium,” Ph. D. Thesis, Univer- sité Claude Bernard, Lyon, 1997. [53] R. Prosmiti, P. Villarreal and G. Delgado-Barrio, “Struc- tures and Energetics of Hn Clusters (n = 5 - 11),” Journal of Physical Chemistry A, Vol. 107, No. 23, 2003, pp. 4768-4772. http://dx.doi.org/10.1021/jp0347318 [45] B. Farizon, M. Farizon, M. J. Gaillard, E. Gerlic, S. Louc, N. V. de Castro Faria and G. Jalbert, “Direct Observation of Multi-Ionization and Multifragmentation in High Ve- locity Cluster Atom Collision,” Chemical Physics Letters, Vol. 252, 1996, p. 147.
|