A Quantum Monte Carlo Study of Lanthanum
Open Access WJCMP
206
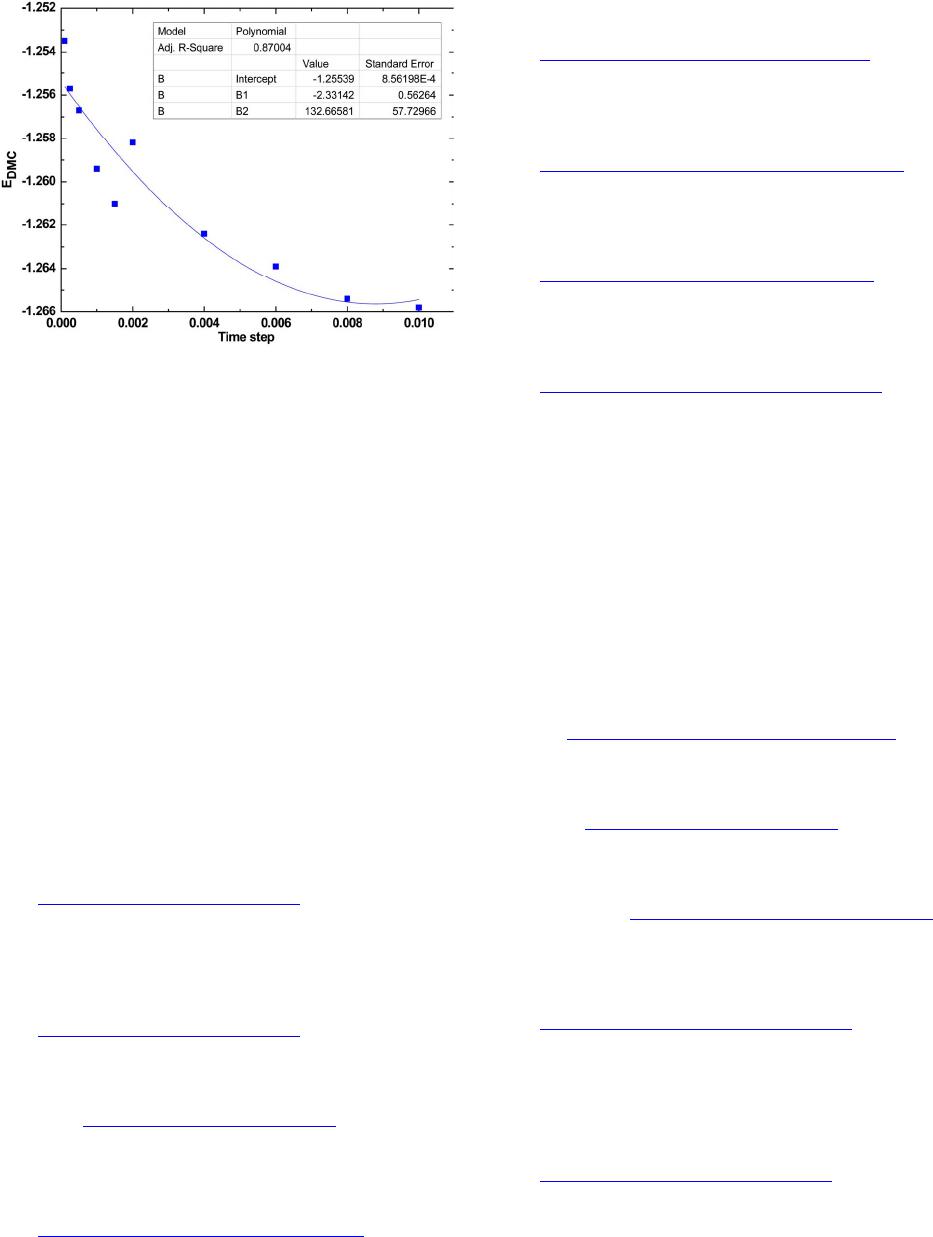
Figure 1. Time step dependence of the diffusion Monte
Carlo (DMC) energies for La atom.
the DMC energies and the time steps follows a polyno-
mial relationship, this is because the presence of Jastrow
factor that introduces polynomial behavior in the energy
as a function of time step. We performed a polynomial
extrapolation of the energies to zero time step. The ex-
trapolated value at τ = 0 for La is −1.25659 ± 0.000839 H.
For the smallest time step, τ = 0.0001 H−1, we found a
time step error of 0.0019 H and for the largest time step,
τ = 0.01 H−1, a value of −0.0104 H has been found.
In conclusion, the small statistical errors which have
been reported for La and its charged cations in this paper
open the way to the possibility for performing high ac-
curacy QMC calculations for the lanthanides.
REFERENCES
[1] M. D. Brown, J. R. Trail, P. LoPez Rios and R. J. Needs,
“Energies of the First Row Atoms from Quantum Monte
Carlo,” The Journal of Chemical Physics, Vol. 126, No.
22, 2007, Article ID: 224110.
http://dx.doi.org/10.1063/1.2743972
[2] J. Toulouse and C. J. Umrigar, “Full Optimization of
Jastrow-Slater Wave Functions with Application to the
First-Flow Atoms and Homonuclear Diatomic Mole-
cules,” The Journal of Chemical Physics, Vol. 128, No.
17, 2008, Article ID: 174101.
http://dx.doi.org/10.1063/1.2908237
[3] K. E. Schmidt and J. W. Moskowitz, “Correlated Monte
Carlo Wave Functions for the Atoms He through Ne,”
The Journal of Chemical Physics, Vol. 93, No. 6, 1990, p.
4172. http://dx.doi.org/10.1063/1.458750
[4] S. D. Kenny, G. Rajagopal and R. J. Needs, “Relativistic
Corrections to Atomic Energies from Quantum Monte
Carlo Calculations,” Physical Review A, Vol. 51, No. 3,
1995, pp. 1898-1904.
http://dx.doi.org/10.1103/PhysRevA.51.1898
[5] E. Buendia, F. J. Galvez and A. Sarsa, “Correlated Wave
Functions for the Ground State of the Atoms Li through
Kr,” Chemical Physics Letters, Vol. 428, No. 4-6, 2006,
pp. 241-244.
http://dx.doi.org/10.1016/j.cplett.2006.07.027
[6] L. Wagner and L. Mitas, “A Quantum Monte Carlo Study
of Electron Correlation in Transition Metal Oxygen
Molecules,” Chemical Physics Letters, Vol. 370, No. 3-4,
2003, pp. 412-417.
http://dx.doi.org/10.1016/S0009-2614(03)00128-3
[7] X. P. Li, D. M. Ceperley and R. M. Martin, “Cohesive
Energy of Silicon by the Green’s-Function Monte Carlo
Method,” Physical Review B, Vol. 44, No. 19, 1991, pp.
10929-10932.
http://dx.doi.org/10.1103/PhysRevB.44.10929
[8] A. Ma, N. D. Drummond, M. D. Towler and R. J. Needs,
“All-Electron Quantum Monte Carlo Calculations for the
Noble Gas Atoms He to Xe,” Physical Review E, Vol. 71,
No. 6, 2005, Article ID: 066704.
http://dx.doi.org/10.1103/PhysRevE.71.066704
[9] J. B. Anderson, “Quantum Monte Carlo. Origins, Devel-
opment, Applications,” Oxford University Press, Oxford,
2007.
[10] M. P. Nightingale and C. J. Umrigar, “Quantum Monte
Carlo Methods in Physics and Chemistry,” Kluwer Aca-
demic Publishers, Berlin, 1999.
[11] L. M. Sobol, “A Primer for the Monte Carlo Method,”
CRC Press, Boca Raton, 1994.
[12] C. J. Cramer, “Essentials of Computational Chemistry:
Theories and Models,” John Wiley & Sons Ltd, England,
2004.
[13] W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Ra-
jagopal, “Quantum Monte Carlo Simulations of Solids,”
Reviews of Modern Physics, Vol. 73, No. 1, 2001, pp. 33-
83. http://dx.doi.org/10.1103/RevModPhys.73.33
[14] J. B. Anderson, “Quantum Chemistry by Random Walk.
H 2P, H+3 D3h 1A′1, H2 3Σ+u, H4 1Σ+g, Be 1SJ,” The
Journal of Chemical Physics, Vol. 65, No. 10, 1976, p.
4121. http://dx.doi.org/10.1063/1.432868
[15] A. Alkauskas, P. Deàk, J. Neugebauer, A. Pasquarello
and C. Van de Walle, “Advanced Calculations for Defects
in Materials,” Wiley-VCH Verlag & Co. K GaA, Wein-
heim, 2011. http://dx.doi.org/10.1002/9783527638529
[16] L. K. Wagner, M. Bajdich and L. Mitas, “Qwalk: A
Quantum Monte Carlo Program for Electronic Structure,”
Journal of Computational Physics, Vol. 228, No. 9, 2009,
pp. 3390-3404.
http://dx.doi.org/10.1016/j.jcp.2009.01.017
[17] M. W. Schmidt, J. A. Boatz, K. K. Baldridge, S. T. Elbert,
M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K.
A. Nguyen, S. Su, T. L. windus, M. Dupuis and J. A.
Montgomery, “General Atomic and Molecular Electronic
Structure System,” Journal of Computational Chemistry,
Vol. 14, No. 11, 1993, 1347-1363.
http://dx.doi.org/10.1002/jcc.540141112
[18] https://bse.pnl.gov/bse/portal
[19] C. E. Moore, “Ionization Potential and Ionization Limits
Derived from the Analyses of Optical Spectra,” National
Bureau of Standards, Washington, 1970.