Applied Mathematics, 2011, 2, 241-246
doi:10.4236/am.2011.22027 Published Online February 2011 (http://www.SciRP.org/journal/am)
Mathematical Modeling of Diffusion Phenomenon in a
Moderately Constricted Geometry
Shailesh Mishra, Narendra Kumar Verma, Shafi Ullah Siddiqui
Department of Mathematics, Harcourt Butler Technological Institute, Kanpur, India
Received October 30, 2010; revised December 19, 2010; accepted December 24, 2010
Abstract
The incorporation of fluid flow through modelled normal and stenosed capillary-tissue exchange system has
highlighted issues that may have major applications for the study of diffusion phenomenon. Results clearly
demonstrate the important roles played by various physiological characteristics and diffusion variables in-
volved in the analysis on blood flow. Assessment of the severity of the disease could be made possible
through the variation of a parameter named as retention parameter. An attempt has been made to study the
effects of local variation of viscosity on flow, wall-shearing stress and distribution of dissolved material in
diseased artery as compared to the normal.
Keywords: Stenosis, Diffusion, Wall Shear Stress, Viscosity, Retention Parameter
1. Introduction
Atherosclerosis is a chronic disease which involves the
build up of cholestero l and othe r fatty deposits within the
arterial wall leading to the narrowing of the blood vessel
lumen (Figure 1). This has the consequence of restrict-
ing blood flow to vital organs which can eventually lead
to various clinical syndromes such as heart attacks and
strokes. These events are the leading causes of death in
the developed world [1,2].
The early events leading to atherosclerosis occur in the
space between the endothelial cells and the smooth mus-
cle cells, a region of the blood vessel known as the sub-
endothelium or intima. The process leading to the cho-
lesterol deposits begins with the formation of fatty str-
eaks. Accumulation of cholesterol within cells leads to
the formation of ‘foam cells’ which reside in this intimal
region of the vessel wall and constitute the fatty streak.
At this stage no symptoms will be observed and in fact
symptoms of atherosclerosis often do not reveal them-
selves until complications such as angina and coronary
artery disease arise. The fatty streaks are often present in
childhood and may not always progress to form the pla-
ques which can be found in affected adults [3]. The dis-
ease may remain asymptomatic for many years. However,
critical restriction of blood flow or thrombosis leading to
total occlusion of the vessel may lead to cardiovascular
events such as heart attack or stroke later in life.
While modeling blood flow in a stenosed tube, it was
initially assumed that, the flow obeys Newtonian hypo-
thesis and the flow variables have been computed by
using basic Navier-Stoke’s equation [4,5]. Later, the
model has been extended by assuming that, it obeys non-
Newtonian hypothesis and showed that under low shear
rates, the model could be best described by this represen-
tation.
The papers [6-10] provide a small sample of the re-
search on non-Newtonian effects on blood flo w. Perkkio
and Keskinen [11] studied the effects of the concentra-
tion on viscosity and the effects of the concentration on
blood flow through a vessel with stenosis and found it an
important aspect from physiological point of view. Kang
and Eringen [12] have also discussed the effects of the
variation of the concentration of the suspended cells of
the blood. Viscosity depending on the local variation of
the concentration of the suspended cells has been intro-
duced by Tandon et al. [13,14]. In the present analysis an
attempt has been made to study the effects of local varia-
tion of viscosity on flow, wall shearing stress and diffu-
sion of dissolved material (nutrients) in diseased artery
as compared to the normal. This work may help in early
identification, diagnosis and treatment of cardiovascular
disorders. Increasing values of
M
represent growth of
new cells which interns increases the viscosity. The re-
sistance to flow (

) increases with the growth of steno-
sis and with the increasing values of the parameter


S. MISHRA ET AL.
242
(a)
(b)
Figure 1. (a) Cross section of a normal artery lumen. The
endothelial cells neighbour the lumen and no intimal thick-
ening is present; (b) Sever atherosclerosis. On the right a
calcified plaque has formed pushing against the endothelial
cells them to bulge into the lumen restricting blood flow.
and
M
. Variation of wall shearing stress (
s

) with the
developing stenosis for different values of parameter

are similar as for resistance to flow. It is seen that in-
creasing values of N describe the increase in retention
of the solutes within the cap illary.
Consider the flow of blood through a circular tube of
radius R(z) whose viscosity varies along the radial direc-
tion. In the capillary segment the geometry of the steno-
sis is given by
 
1
0
0
1
1
m
m
o
A
Lzd zddzdL Rz
Rotherwise







(1)
Here the parameter
A
is expressed as

1
0
01
mm
m
Lm
ARm


 (2)
where

denotes the maximum height of the stenosis at

0
/1mm
L
zdm
 such that
0
1
R

.()Rz and 0 R is
the radius of capillary with and without stenosis respec-
tively (see Figure 2).
2. Formulation of the Problem
The flow is considered to be steady, fully develop ed and
laminar viscous flow of suspensions of cells. For dilute
suspensions, a reasonable approximation to the viscosity
of the suspension may be described as


01C
   (3)
where

and 0

denote the viscosity of blood and
plasma respectively.
The concentration C is determined by the governing
diffusion equation
2
2
10 CC
DM
rr r
 






(4)
where D is the diffusion coefficient and
M
is the rate
of production or degeneration.
The concentration equation for the solute is expressed
as
2
11 11
12
1
CC CC
uD
tz rr r

 
 


 

(5)
where 1
C represents the concentration of the solute,
u is the axial velocity and 1 D the diffusion coefficient
for the solute under cons ideration in the blood.
The equations governing the flow of blood in the ar-
terial system are given by
0pu r
zrrr




 



(6)
0p
r

 (7)
To solve the above system of equations, the following
boundary and matching conditions are introduced:
Figure 2. Flow geometry of stenosed capillary.

S. MISHRA ET AL.
243
1
1
11
0
0, at0
., at
0, at0
0, at
0, at0
.. , at
,at 0
,at
L
Cr
r
C
DVCrR
r
ur
r
urR
Cr
r
C
DVNCrR
r
pp z
pp zL

 


 


 

 

 



 


 

 
(8)
3. Solution of the Problem
The expression for concentration C is obtained by solv-
ing Equation (4) using the boundary conditions given in
Equation (8) as

222
4
M
CVRrDR
DV



(9)
The expression for the viscosity is given by
2
01 2
A
rA 



(10)
where 14
M
AD

 and

2
212
4
M
A
VR DR
DV

 .
On solving Equation (6) with the help of boundary
conditions mentioned in Equation (8) we obtained the
velocity distribution

22 44 1
20 2
1
42
Ap
uRrRr
A
Az 


 



(11)
The volumetric rate of flow is defined as
2
0
Rdu
Qr dr
dr





 (12)
By performing the integration of Equation (12), using
Equation (11), one obtains
6 41
20 2
243
AR Rp
Q
A
Az


  
 





(13)
The pressure gradi ent is thus obtained as
2
()
dp Q
dzI z

 (14)
where
 
3
0
Rrdr
Iz r

.
Integrating Equation (14) and using the boundary con-
dition give n in Equat i on (8) , we have

00
2L
L
Qdz
pp
I
z 
  (15)
The resistance to flow

is defined by


0
L
pp
Q


 (16)
which on solving gives



0
0
0
2dL
d
LL dz
I
Iz



 







 (17)
where

03
00
Rr
I
dr
r 
.
The wall shearing stress is given by

()
R
rRz
du
rdr





(18)
which on using Equation (11) and Equation (15) gives
s

, given by
()
()
s
RzQ
I
z







 (19)
Following Tandon and Pal [13] the apparent viscosity
is expressed as
1
6 412
02 2
4
3
app
AR
R
AA





 



 (20)
To solve the concentration equation for the solute
given by Equation (5), following non-dimensional quan-
tities are introduced:


1
1
1000
,,, ,,
zut C
tLr R
ttC R
tuLRC R


 
(21)
so that Equation (5) becomes
2
1 111
1
22
10
CDC C Ct
tLR


 
  
 
 
 
 
(22)
together with the boundary conditions:
11
11
0
0, at0;..,at
CCR
DVNC
R




 



 (23)
where uu


, N is the retention parameter and
42
0
20
4
RR p
uAL




 (24)
and V is the radial velocity of the wall, given by
dR
Vdt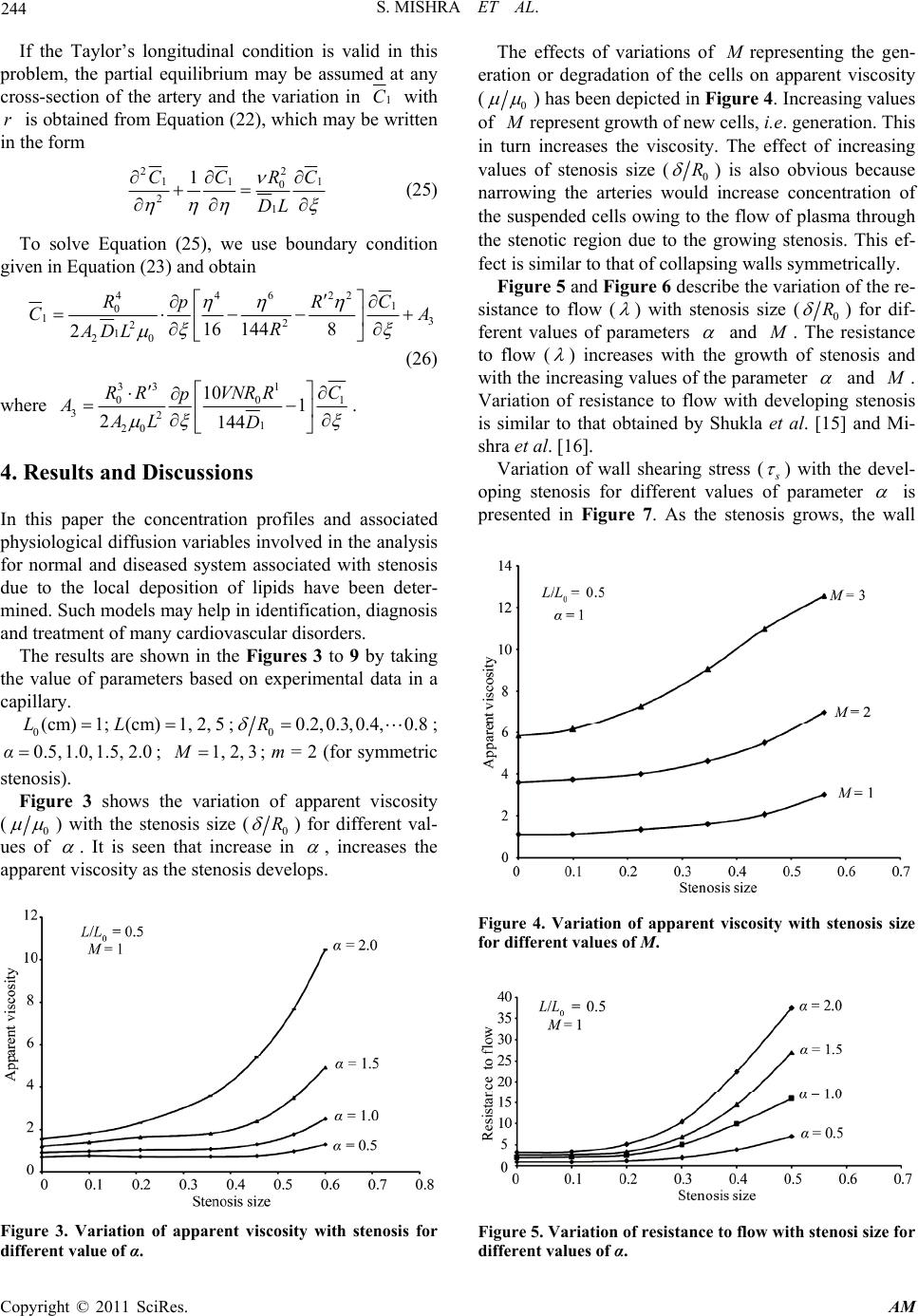



S. MISHRA ET AL.
244
If the Taylor’s longitudinal condition is valid in this
problem, the partial equilibrium may be assumed at any
cross-section of the artery and the variation in 1
C with
r is obtained from Equation (22), which may be written
in the form
2
211 1
0
21
1R CC C
DL




 


 (25)
To solve Equation (25), we use boundary condition
given in Equation (23) and obtain
446 22
1
0
13
2
2
1
20
16 8 144
2
RpRC
CA
R
ADL
 


 





(26)
where 33 1
00 1
321
20
10 1
2144
RRVNRR C p
AAL D

 
 






.
4. Results and Discussions
In this paper the concentration profiles and associated
physiological diffusion variables involved in the analysis
for normal and diseased system associated with stenosis
due to the local deposition of lipids have been deter-
mined. Such mo dels may help in id entification , diag nosis
and treatment of many cardiovascular di s o rd ers.
The results are shown in the Figures 3 to 9 by taking
the value of parameters based on experimental data in a
capillary.
0(cm) 1;(cm) 1,2,5LL;00.2,0.3,0.4, 0.8R

;
0.5,1.0,1.5, 2.0α; 1,2, 3M; m = 2 (for symmetric
stenosis).
Figure 3 shows the variation of apparent viscosity
(0

 ) with the stenosis size (0 R

) for different val-
ues of

. It is seen that increase in

, increases the
apparent viscosity as the stenosis develops.
Figure 3. Variation of apparent viscosity with stenosis for
different value of α.
The effects of variations of
M
representing the gen-
eration or degradation of the cells on apparent viscosity
(0

 ) has been depicted in Figure 4. Increasing values
of
M
represent growth of new cel ls , i.e. generation. This
in turn increases the viscosity. The effect of increasing
values of stenosis size (0 R

) is also obvious because
narrowing the arteries would increase concentration of
the suspended cells ow ing to the flow of plasma through
the stenotic region due to the growing stenosis. This ef-
fect is similar to that of collapsing walls symmetrically.
Figure 5 and Figure 6 describe the variation of the re-
sistance to flow (

) with stenosis size (0 R

) for dif-
ferent values of parameters

and
M
. The resistance
to flow (

) increases with the growth of stenosis and
with the increasing values of the parameter

and
M
.
Variation of resistance to flow with developing stenosis
is similar to that obtained by Shukla et al. [15] and Mi-
shra et al. [16].
Variation of wall shearing stress (
s

) with the devel-
oping stenosis for different values of parameter

is
presented in Figure 7. As the stenosis grows, the wall
Figure 4. Variation of apparent viscosity with stenosis size
for different values of M.
Figure 5. Variation of resistance to flow with stenosi size for
different values of α.

S. MISHRA ET AL.
245
shearing stress (
s

) increases. The results for increasing
values of

are similar to for resistance to flow.
Figure 8 reveals the effect of retention parameter (N)
on concentration in capillary. Increasing values of N de-
scribe the increase in retention of the solutes within the
capillary. N=1 implies the complete retention, i.e., no
solute or fluid diffuses and as the retention parameter
decreases from 1 to 0.4 more solute diffuses, which in
turn, decreases the solute concentration in the capillary
region. The variation of the values of retention parameter
in the stenotic region may also be associated with the
type of plaques deposited on the walls: calcified, fibrous
or fatty plaques.
Figure 9 shows the diffusion of large and small mo-
lecular weight nutrients within the capillary for different
values of stenosis size (0 R

).
Large molecular weight nutrients face more resistance
to diffuse into the tissue and therefore the cells of the
deeper region are deprived of getting sufficient nutritio n.
Similar results have been obtained by Tandon et al. [13].
Figure 6. Variation of resistance to flow with stenosi size for
different values of M.
Figure 7. Variation of wall shear stress with stenosis size for
different values of α.
Figure 8. Concentration profiles for different values of re-
tention parameter (N).
Figure 9. Concentration profiles for different values of ste-
nosis size δ/R0.
5. Concluding Remarks
The problem relating capillary-tissue exchange pheno-
menon is mixed coupled boundary problem. This model
has incorporated simultaneous dispersion of solute in
capillary in normal and stenotic condition depending on
various parameters including retention parameters. The
results are more encouraging and correlating well with the
experimental observation that deeper region cells are de-
prived of the nutrients in the stenotic region. There is a
need to pursue inter-disciplinary research at a greater pace
for further de v el opment from cli ni c al poi nt o f vi ew.
6. References
[1] V. W. Bowry and K. U. Ingold, “The Unexpected Role of
Vitamin E (α-Tocopherol) in the Peroxidation of Human
Low-Density Lipoprotein,” Accounts of Chemical Re-
search, Vol. 32, No. 1, 1999, pp. 27-34.

S. MISHRA ET AL.
246
doi:10.1021/ar950059o
[2] M. J. Davies and N. Woolf, “Atherosclerosis in Ischaemic
Heart Disease: The Mechanisms,” Science Press, London,
1990.
[3] H. Esterbauer, J. Gebicki, H. Puhl and G. Jurgens, “The
Role of Lipid Peroxidation and Antioxidants in Oxidative
Modification of LDL,” Free Radical Biology and Medi-
cine, Vol. 13, No. 4, 1992, pp. 341-390.
doi:10.1016/0891-5849(92)90181-F
[4] B. V. R. Kumar and K. B. Naidu, “A Pulsatile Suspen-
sion Flow Simulation in a Stenosed Vessel,” Mathemati-
cal and Computer Modeling, Vol. 23, No. 5, 1996, pp.
75-86. doi:10.1016/0895-7177(96)00013-1
[5] P. N. Tandon and U. V. S. Rana, “A New Model for
Blood Flow through an Artery with Axisymmetric Steno-
sis,” International Journal of Biomedical Computing, Vol.
38, No. 3, 1995, pp. 257-267.
doi:10.1016/S0020-7101(05)80008-X
[6] F. J. H. Gijsen, F. N. van de Vosse and J. D. Janssen,
“The Influence of the Non-Newtonian Properties of Blood
on the Flow in Large Arteries: Steady Flow in a Carotid
Bifurcation Model,” Journal of Biomechanics, Vol. 32,
No. 6, 1999, pp. 601-608.
doi:10.1016/S0021-9290(99)00015-9
[7] B. Johnston, P. R. Johnston, S. Corney and D. Kilpatrick,
“Non-Newtonian Blood Flow in Human Right Coronary
Arteries: Steady State Simulations,” Journal of Biome-
chanics, Vol. 37, No. 5, 2004, pp. 709-720.
doi:10.1016/j.jbiomech.2003.09.016
[8] A. Leuprecht and K. Perktold, “Computer Simulation of
Non-Newtonian Effects on Blood Flows in Large Arte-
ries,” Computer Methods in Biomechanics & Biomedical
Engineering, Vol. 4, No. 2, 2001, pp. 149-163.
doi:10.1080/10255840008908002
[9] P. Neofytou and D. Drikakis, “Non-Newtonian Flow In-
stability in a Channel with a Sudden Expansion,” Journal
of Non-Newtonian Fluid Mechanics, Vol. 111, No. 2-3,
2003, pp. 127-150. doi:10.1016/S0377-0257(03)00041-7
[10] K. K. Yeleswarapu, “Evaluation of Continuum Models
for Characterizing the Constitutive Behavior of Blood,”
Ph.D. Thesis, Department of Mechanical Engineering,
University of Pittsburgh, Pittsburgh, 1996.
[11] J. Perkkio and R. Keskinen, “Hematocrit Reduction in
Bifurcation due to Plasma Skimming,” Bulletin of Mathe-
matical Biology, Vol. 45, No. 1, 1983, pp. 41-50.
[12] C. K. Kang and A. C. Eringen, “The Effect of Micro-
structure on the Rheological Properties of Blood,” Bulle-
tin of Mathematical Biology, Vol. 38, No. 2, 1976, pp.
135-159.
[13] P. N. Tandon and T. S. Pal, “On Transmural Fluid Ex-
change and Variation of Viscosity of Blood Flowing
through Permeable Capillaries,” Medical and Life Science
Engineering, Vol. 5, No. 1, 1979, pp. 18-29.
[14] P. N. Tandon and R. Agarwal, “A Study on Nutritional
Transport in Synovial Joints,” International Journal of
Computers and Mathematics with Application, Vol. 17,
No. 7, 1989, pp. 1101-1141.
[15] J. B. Shukla, R. S. Parihar and B. R. P. Rao, “Effects of
Stenosis on Non-Newtonian Flow of the Blood in an Ar-
tery,” Bulletin of Mathematical Biology, Vol. 42, No. 3,
1980, pp. 283-294.
[16] J. C. Mishra and S. Chakravarty, “Flow in Arteries in the
Presence of Stenosis,” Journal of Biomechanics, Vol. 19,
No. 11, 1986, pp. 907-918.
doi:10.1016/0021-9290(86)90186-7