Paper Menu >>
Journal Menu >>
 Energy and Power E ngineering, 2013, 5, 1266-1272 doi:10.4236/epe.2013.54B240 Published Online July 2013 (http://www.scirp.org/journal/epe) Copyright © 2013 S ciRes. EPE Analysis of a Large Groundin g System and Subsequent Field Test Validation Using the Fall of Potential Method Huan Huang1, Hualin Liu1, Hong Luo1, Hao Du1, Yi Xing1, Yexu Li2, Farid P. Dawalibi2, Haijun Zhou2, Longhai Fu2 1Guizho u Electri c Power Test & Research Institute, Guiyang, China 2Safe Engin eering Services & technologies ltd, Blvd. Des Ois eaux, Laval, Québec, Canada Email: info@sestech.com Received April, 2013 ABSTRACT This paper examines various aspects of the design process and subsequent field test measurements of a large and com- plex s ub st at io n gro u nd in g s yst e m. T he st ud y a nd mea sur e ments show that soil layering and lead interference can have a significant impact on the appropriate test location that yields the exact substation ground impedance. Applying a spe- cific percentage rule such as the 61.8% rule for uniform soils to obtain the true ground impedance may lead to unac- cep ta bl e e rr or s fo r l ar ge gr o un di ng s ys te ms. T hi s p o ses s i gni fic a nt p r ob l ems whe n a ttempting to va li da te a d e sig n b ase d on raw test data that are interpreted using approximate methods to evaluate substation ground impedance, and determine ground potential rise (GPR), touch and step voltages. Advanced measurement methodologies and modern software packages were used to obtain and effectively analyze fall of potential test data, compute fault current distribution, and evalua te touch and step voltages for this lar ge substation. Fault current distribution between the grounding system and other metallic paths were computed to determine the portion of fault current discharged in the grounding system. The performance of the grounding system, including its GPR and touch and step voltages, has been accura tely computed and measured, taking into account the impedance of the steel material used of the ground conductors and circulating cur- rents withi n the sub s tat io n gr ound i n g syst e m. Keywords: Ground Resista nce; Fal l-of-Potential; Ground Impedance Measure ment; Ground Potential Rise; Ground Potential Difference; Touch Voltage; Step Voltage; Steel Conductors 1. Introduction Appropriate power system grounding is important for maintaining reliable operation of electric power systems, protecting equipment, and insuring the safety of public and personnel. A grounding system must be properly designed and its performance needs to be evaluated. Im- proper or inaccurate analysis can lead to significant ex- penses due directly to unnecessary over design or as a result of subsequent corrective measures caused by fail- ures of the inadequate design. Most electrical engineers understand the importance of grounding system to dis- charge safely phase-to-ground faults into the sur round in g soil. Unfortunately, the complex and non-homogeneous nature of the soil, the intricate three-dimensional shape of the grounding system and topology of the entire power system network result in a very difficult ta sk that requires appropriate specialized software packages and skilled professionals with adequate expertise in this field in order to account for the numero us factors that have t o be considered during the design process and subsequent field measure ment validation task. It is often necessar y to measure the ground impedance of a grounding system in order to validate a grounding analysis. The basic technique which is almost universally used for the measurement of grounding system imped ance is known a s the Fal l-of-Potential method. T he Fall-of-Potential method introduces two auxiliary electrodes, called return electrode and potential probe. When the return electrode is placed at a finite distance from the grounding system and the potential probe is driven into the earth at a specific location(the so-called “exact potential probe location”) then an accurate measurement of the ground imp edance is obtained. For uniform soils and large distances between the grounding system and the return electrode, it is well known that t he exact poten tial prob e location follo ws the 61.8% rule, i.e., the exact locatio n for the potential prob e is r = 0.618D, where r and D are the distances from the center of the gro undi ng s yste m to the p ot entia l pr obe and to the current electrode, respectively. It is important to understand that the 61.8% rule is based on the  H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1267 assumption that the soil is uniform and that the grounding electrode is small or hemispherical and that the potential probe and current electrode are also hemispherical or small. For two-layer soils, a classical paper [3] has shown that the exact locations can vary from values close to 50% to values exceeding 90% depending on the nature of the t wo -l ayer s o il struct ure an d thick ness of the top la yer. This finding was included in Guide IEEE 81 -1983 [15] and was mysteriously removed in the 2001 edition before being reintroduced in the 2013 edition! In other words, the exact location of the potential probe is well defined for some ideal cases, such as hemispherical or small grounding electrodes buried in uniform or layered soils [1-6] but must be evaluated adequately when the separation distances are not large enough. In such cases, a value read at 61.8% may lead to significant errors on the measured ground impedance. The exact potential probe position must therefore be determined each time, using appropriate computer simulations. Many grounding systems in China and several other countries are made of steel, which has higher permeability and lower conductivity than copper [7-11]. This raises some unique issues, particularly if the substation size is lar ge and the soil resisti vity is lo w. In a conventional grounding analysis approach, a grounding system is generally assumed as an equipotent structure. This would be inaccurate for most cases where steel grounding systems are used. In fact, the ground impedance of the grounding system has a significant inductive component, which is not take n into account b y classical groundin g analysis metho ds. The analysis of the grounding system of an existing 500 kV large substation is summarized in this paper. The substation includes 500 kV, 220 kV and 35 kV switchyards. T wo500 kV and seve n 220 kV transmission lines enter the substation. Figure 1 is a plan view of the substation grounding system. The ground conductors are buried at a depth of 0.8 m and are made of L60*6 mm steel conductors. A number of ground rods are installed at various locations of the gr id . They are 2 .5 m long and are made of L60*3.5 mm steel conductors. Figure 2 is a plan view of the substation grounding system and the electrical network connected to it. Figure 2 also provides the soil resist ivity measure ment locations: one is inside the substation while another one is outside the substatio n. Figure 3 represents the multiphase circuit for a single-line-to-gro und fault in the 2 20 kV sub statio n yard. It shows the equivalent circuit of the computer model used. Figure 4 shows a typical cross section of all the transmission line towers modeled. A tower resistance of 15 or 20 ohms was used depending on the type of tower structure grou nds. Figure 1 . Plan view of the g r o unding sy stem. Figure 2. Plan view of the grounding system and the net- w ork connected to it. Figure 3. Simplified circuit model for fault current split calculations.  H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1268 Figure 4 . Typical cross section of the transim msiosn lines. To evaluate the grounding performance of the large syste m ground net work, the follo wing steps were carried out: 1) Soil resistivity and grid impedance measurements and interpretation; 2) Fault current split calculations; 3) Groundin g system performance analysis. This pap er is not intended to repor t detailed grounding design issues and results but rather to highlight the vari- ous challenges encountered and their ramifications, if these challenges are ignored or if simplifying assump- tions are made in place of a detailed grounding analysis. The results presented in this paper provide useful in- sight and information for accurately measuring the ground impedance of large grounding systems, for inter- pre ting the mea sure ment s and for evalua ti ng safe ty in t he station. The analysis and the discussions can be used as a reference guide to st udy lar ge grounding sys t ems. 2. Resistivity Measurements and Interp ret ation Soil resistivity measurements were made along two trave r ses a t t he s ub sta t io n si te , usi ng the W enne r fo ur -pin method. Measurements along the short traverse inside the substation were carried out in order to obtain shallow depth resisti vities at the pro ject site. Measure ments alon g one long traverse outside the substation were carried out in order to obtain soil resistivitie s at la rger depths. The measured soil resistivity data were interpreted us- ing the RESAP computation module of the CDEGS software package [12]. Based on the principle that short traverse measurements determine shallow depth soil re- sistivity and large spacing measurements determine deep soil resistivity, a three-layer soil model was constructed, which is representative of the soil structures at the site and is expected to be conservative for the grounding analysis. The selec te d soil mo del is shown in Table 1. 3. Grounding Impedance Measurement and Interp ret ation To evaluate the performance of a substation grounding system, the ground impedance of the grounding system must be obtained either by measurement or by com- putation with appropriate soil resistivity measurements. Incorrect ground impedance will lead to incorrect fault curr ent co mputati on, ther efore affecting the results of the analysis. Ideally, the ground impedance should be computed and then validat ed by measurement. For this practical case study, due to the dense transmission line area and the expected low impedance measurement, a high current test unit was used. According to IEEE 81.2, it is recommended that the current probe has a minimum length of 6.5 times the diagonal of the substation. The substation is surrounded by difficult terrains. Fortunately, a small road was available along the west side of the substation. Therefore, the fall of potential test that followed this road was used to perform the measurements. Figures 5 and 6 illustrate the test setup which was carried out for multiple frequencies of 47, 46, 53 and 54 Hz for each test point. The fall of potential test results are summarized in Figure 7 (red dots). The next stage of the analysis was to model the fall of potential test, using the soil model developed from measured soil resistivity data (shown in Table 1). The first challenge was to determine how much of the overall transmiss ion line gr ounding network is re ally i nflue ncin g Table 1. Selected soil model. Layer Resistivity ( Ω -m) Thickness (m) Top 320 0.35 Ce ntral 65 2.0 Bottom 420 infinite Figure 5 . Fall of potenti al test setup (complet e model). 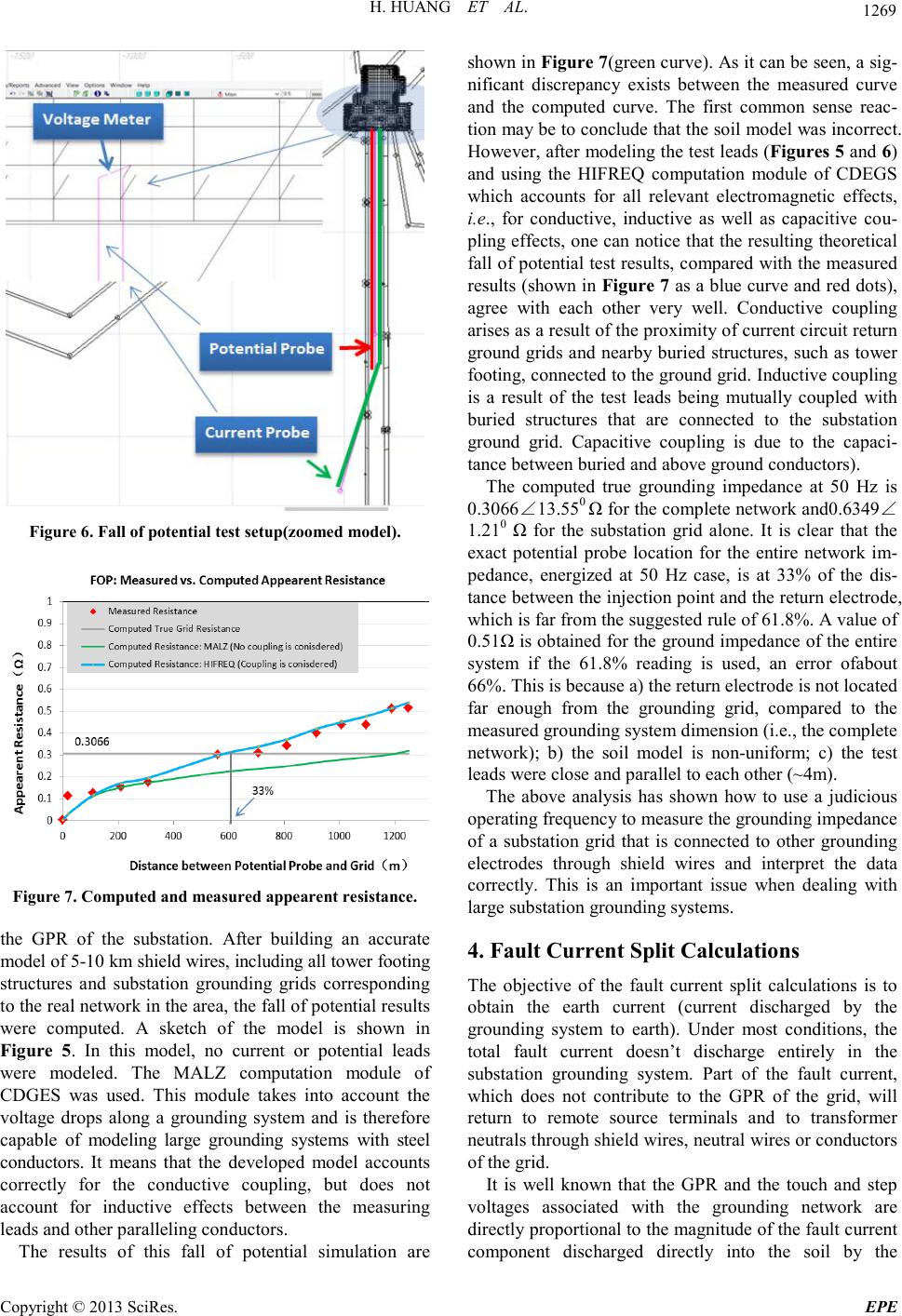 H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1269 Figure 6 . Fall of potential test setup(zoomed model). Figure 7 . Computed a nd measured appearent resista nc e. the GPR of the substation. After building an accurate model of 5-10 km shield wires, incl udi ng all to wer foo ting structures and substation grounding grids corresponding to the real network in the area, the fall of potential r es ults were computed. A sketch of the model is shown in Figure 5. In this model, no current or potential leads were modeled. The MALZ computation module of CDGES was used. This module takes into account the voltage drops along a grounding system and is therefore capable of modeling large grounding systems with steel conductors. It means that the developed model accounts correctly for the conductive coupling, but does not account for inductive effects between the measuring leads and other paralleling conductors. The results of this fall of potential simulation are sho wn in Figure 7(green curv e). As it can be seen, a sig- nificant discrepancy exists between the measured curve and the computed curve. The first common sense reac- tion may be to conclude that the soil model was incorrect. However, after modeling the test leads (Figures 5 and 6) and using the HIFREQ computation module of CDEGS which accounts for all relevant electromagnetic effects, i.e., for conductive, inductive as well as capacitive cou- pling effects, one can notice that the resulting theoretical fall of potential te st results, co mpared with the measured resul ts (sho wn in Figure 7 as a blue curve and red dots), agree with each other very well. Conductive coupling arises as a result of the proximity of current circ uit return ground grids and nearb y buried structures, such as tower footing, connected to the ground grid. Inductive coupling is a result of the test leads being mutually coupled with buried structures that are connected to the substation ground grid. Capacitive coupling is due to the capaci- tance between buried and above ground conductors). The computed true grounding impedance at 50 Hz is 0.3066∠13.550 Ω for the complete network and0.6349∠ 1.210 Ω for the substation grid alone. It is clear that the exact potential probe location for the entire network im- pedance, energized at 50 Hz case, is at 33% of the dis- tance between the injection point and the return electrode, whic h is fa r from the s ugge s te d r ule o f 61. 8 %. A value o f 0.51Ω is obtained for the ground impedance of the entire system if the 61.8% reading is used, an error ofabout 66%. This is because a) the return electrode is not located far enough from the grounding grid, compared to the measured grounding system dimension (i.e., the complete network); b) the soil model is non-uniform; c) the test leads were close and parallel to each other (~4m). The above analysis has shown how to use a judicious ope r ati ng fre q ue nc y to mea s ur e the gro und i ng i mp ed a nce of a substation grid that is connected to other grounding electrodes through shield wires and interpret the data correctly. This is an important issue when dealing with large substa t ion grounding systems. 4. Fault Current Split Calculations The objective of the fault current split calculations is to obtain the earth current (current discharged by the grounding system to earth). Under most conditions, the total fault current doesn’t discharge entirely in the substation grounding system. Part of the fault current, which does not contribute to the GPR of the grid, will return to remote source terminals and to transformer neutra l s t hr o ug h shi e ld wir es, neut ra l wire s o r co nd uct or s of the grid. It is well known that the GPR and the touch and step voltages associated with the grounding network are directl y proportional to the magnitude of the fault current component discharged directly into the soil by the  H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1270 ground in g net work. It i s therefore important to determine how much of the fault current returns to remote sources via overhead ground wires and neutral wires of the transmission lines and distribution lines connected to the substation. Computer simulations have been performed using the Right-Of-Way software package described in [12] based on the circuit model sho wn in Figure 3 and on the com- puted ground impedance of the substation in the soil shown in Table 1. A circuit model representing the sce- nario of a 220 kV single-line-to-ground fault at the power plant is sho wn in F igure 3. Figure 3 al so sho ws the fa ult current contributions from all sources; Figure 8 shows the distrib ution of the fault curre nt along the tr a ns mission line overhead ground wires for a 220 kV single-phase- to-ground fault. Table 2 shows the results of fault curre nt distribution calculation. Note that the local source con- tribution from the 500 kV /220 kV step-up transformers in the substation i s estimated to be about 8 kA, as shown in Table 2. This current was not modeled in the circuit current split calculations because it circulates [13] be- tween the fault location and the step-up transformers via neutra l and gr ound cond uctor s. Howeve r, this cir culati ng curr ent was inc lud ed i n the gr oundi ng s yste m mod el a s it should. Figure 8. Computed fault current in the power line over- head ground wires. Table 2. F a ult c ur rent spli t calculation results. Remote contribution 9.8 ∠ -97.1° kA Local contrib utio n (circulating current) 8.0 ∠ -90.0°kA Total fault current 17.77 ∠ -93.9°kA Current returni ng via OHGW 8.14 ∠ 95.5° kA Earth current discharged in grid 1.78 ∠ 105° kA 5. Grounding System Performance Analysis GPR, touch and step voltages are important quantities when a substation is assessed. The calculation of GPR, touch a nd step vo ltages was car ried out using the M ALZ computatio n module[12], which takes into account attenuation or voltage drop along conductors in a grounding system, avoiding therefore the incorrect assumption that a groundi ng grid is equipot ent ial. In this study case, we have a 500 kV substation at different voltage levels, i.e., 500 kV, 220 kV and 35 kV, fed by several power source terminals at 500 kV and 220 kV. Whe n a sin gle-phase-to-ground fault occurs on a 220 kV bus, the 500 kV side will supply fault currents thro ugh t he 50 0 kV transfo r mers; par t of the fault c urre nt will return to the transformer neutral through the grid conductors (circulating current between the fault location and the trans former neutral po int). Similarly, the fault current is injected at the fault location and a portion of it returns to the remote source through the shield wire con nected to the grid (circulatin g between the fault location and the shield wire connecting point). Because of the low impedance path provided by the ground conduct ors , onl y a ne gligi ble s mal l a mount o f this c ur re nt le a ks o ut from the gr o und c o nd ucto r s to e ar th. As a result, cir c ulating curre nts do not affect s ignificantly the average grid GPR but may distort its shape significantly. However, for a large substation, the distance between the fault location and the transformer neutral point or the shield wire connecting connection point can be quite large. As a result, high potential differences, due to this large circulating current, may exist within the grounding grid. In other words, t he circul ating curr ent co ntribute s to the ground potential differences (GPD) between various locations o f the grid and results in hi gher touch and step volta ge s, es pe ci al l y for a lar ge gro und i ng s yst e m a nd low soil resistivity soil environments. Obviously, ignoring transformer and shield or neutral wirescirculating currents in a groundi ng syst em study can lead to inaccurate designs leading to unsafe situations. A co mputer mod el was buil t f or t he gro undi ng sys te m. Figure 9 shows the model considering all current sources, includin g circul ating currents. The maximum acceptable touch and step voltages are indicated in Table 3 that are calculated based on the fol- lowing criter ia : Method: IEEE Standard 80-2000 [14] Body weight: 50 kg Body resistance: 1000 X/R ratio: 20 Fault duration: 0.12 sec All accessible areas inside and outside the substation, for all possible soil surface covering materials: native soil, crushed rock or asphalt (even very low resistivity materials), had acceptable touch and step voltages under 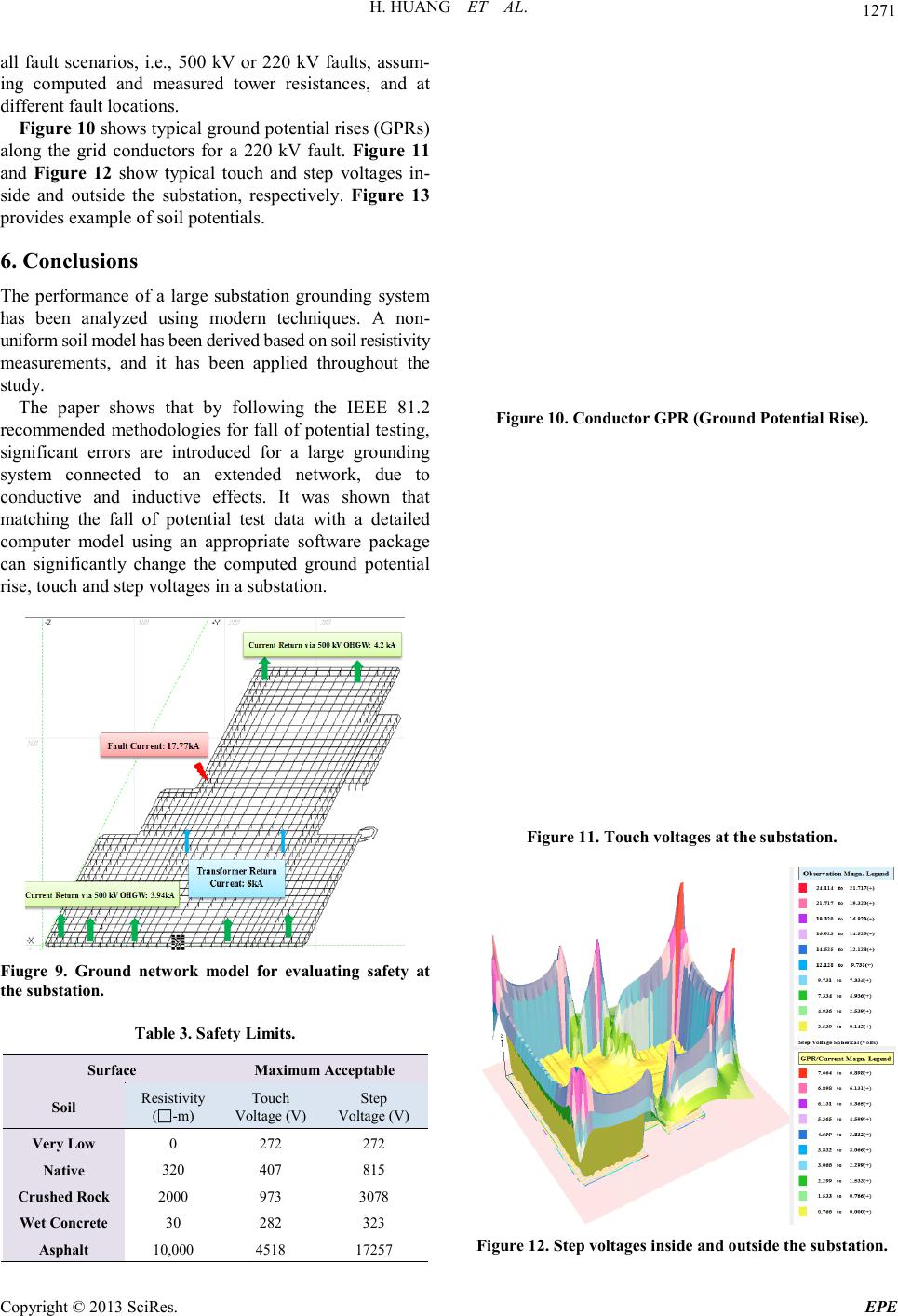 H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1271 all fault scenarios, i.e., 500 kV or 220 kV faults, assum- ing computed and measured tower resistances, and at different fault locations. Figure 10 shows typical ground potential rises (GPRs) along the grid conductors for a 220 kV fault. Figure 11 and Figure 12 show typical touch and step voltages in- side and outside the substation, respectively. Figure 13 provides example of soil pote ntials. 6. Conclusions The performance of a large substation grounding system has been analyzed using modern techniques. A non- uniform soil model has been derived based on soil resistivity measurements, and it has been applied throughout the study. The paper shows that by following the IEEE 81.2 recommended methodologies for fall of potential testing, significant errors are introduced for a large grounding system connected to an extended network, due to conductive and inductive effects. It was shown that matching the fall of potential test data with a detailed computer model using an appropriate software package can significantly change the computed ground potential rise , touch and s t ep voltages in a s ubstation. Fiugre 9. Ground network model for evaluating safety at the substa tion. Table 3. Safety Limits. Surface Maximum Acceptable Soil Resistivity (-m) Touch Voltage (V) Step Voltage (V) Very Low 0 272 272 Native 320 407 815 Crushed Rock 2000 973 3078 Wet Concrete 30 282 323 Asphalt 10,000 4518 17257 Figure 10. Conductor GPR (Ground Potential Ri s e) . Figure 11. Touch voltages at the su bs tation. Figure 12. Step voltages inside and outside t he substation.  H. HUANG ET AL. Copyright © 2013 S ciRes. EPE 1272 Figure 13. Soil Potentials inside and outside the s ubstation. A complete circuit model of the overhead transmission line network has been built in order to determine the current distribution during a single-phase-to-gr ound fa ult. Therefore, current injected into the soil through the grid (which contributes to the GPR, touch and step voltages) was obtained. Due to the large size of the grounding system and to the fact that the grid is made of steel ground conductors, the conventional approach used in grounding analysis (equipotential grounding system) can lead to wrong results. Therefore, adequate methods taking into account voltage drops along the grid conductors and circulating currents within the substation must and have been used to compute the grid GPR, touch and st ep voltages. The procedures presented in this paper can be used as a guide when carrying out grounding analysis of a large po wer substatio n. 7. Acknowled gements The authors wish to thank Mr. J. L. Chagas of SES for his review and comments on the paper man uscrip t. REFERENCES [1] F. P. Dawalibi and D. Mukhekar, “Resistance Measure- ment of Large Grounding Systems,” IEEE Transactions on Power Apparatus and Systems, Vol. PAS-98, No. 6, 1979, pp. 2348-2354. doi:10.1109/TPAS.1979.319434 [2] J. M a and F. P. Dawalibi, “Effects of Inductive Coupling between Leads in Ground Impedance Measurement Using Fall-of-Poten tial M ethod”, in Proc. IEEE /Po wer Eng. Soc. Trans. Dis. Conf. Expo., New Orleans, LA, Apr. 11-16, 1999, pp . 266-271. [3] F. P. Dawalibi and D. Mukhekar, “Ground Electrode Resistance Measurement in Nonuniform Soils,” IEEE Transactions, Vol. PAS-93, No. 1, Jan. 1974, pp. 109-116. [4] J. Ma, F. P. Dawalibi and W. Ruan, “Ground Impedance Measurement and Interpretation in Various Soil Struc- tures,” IEEE/PES Winter Meeting 2000, Singapore, Jan. 23-27, 2000. [5] J. M a and F. P. Dawalibi, “Extended Analysis of Ground Impedance Measurement Using the Fall-of-Potential Me- thod,” I EE E Transac t i ons on P W R D , Vol. 17, No. 4. [6] Y. Li, J. Ma and F. P. Dawalibi, “Impedance Measure- ment of Large Grounding Systems Using the Fall-of-potential Method,” Proceedings of the Third IASTED International Conference on Power and Energy Systems, EuroPES 2003, Marbella, Spain, Sept. 3-5, 2003, pp. 701-706. [7] G. Yu, J. Ma and F. P. Dawalibi, “Effect of Soil Struc- tures on Grounding Systems Consisting of Steel Conduc- tors,” Proceedings of the International Conference on Electrical Engineering (ICEE'2001), Xian, China, July 22-26, 2001. [8] Y. Li, J. Ma and F. P. Dawalibi, “Power Grounding Safe- ty: Copper Grounding Systems vs. Steel Grounding Sys- tems,” International Conference on Power System Tech- nology (POWERCON2006), Chongqing, China, October 22-26, 2006. [9] Y. Li, F. Dawalibi, J. Ma and Y. Yang, “Analysis of A Steel Grounding System: A Practical Case Study,” The 15th Conference on Electric Power Supply Industry (CEPSI) Shanghai, China, October 18-22, 2004. [10] J. Ma and F. P. Dawalibi, “Grounding System Design for a Large Power Plant,” The 4th IASTED Asian Confe- rence on Power and Energy Systems (AsiaPES), Lang- kawi, Malaysia, April 2-4, 2008. [11] J. Ma and F. P. Dawalibi, “Grounding Analysis of a Large Electric Power Station,” International Conference on Power System Technology (Powercon2006), Chongq- ing, China, October 22-2 6, 20 06. [12] CDEGS Software Package, Safe Engineering Services & technologies ltd., Montreal, Quebec, Canada, 1991 - 2012. [13] Y. Li and F. P. Dawalibi, “Practical and Realistic Con- siderations of Fault Current Analysis,” Proceedings of the International Conference on Electrical Engineering (ICEE 2011), Hong Kong, July 10 - 14, 2011. [14] Guide for Safety in AC Substation Grounding, IEEE Std. 80-2000. [15] Guide for Measuring Earth Resistivity, Ground Imped- ance and Earth Surface Potentials of a Ground System, IEEE Std. 81-1983, IEEE. |

