Energy and Power Engineering, 2013, 5, 1243-1248
doi:10.4236/epe.2013.54B236 Published Online July 2013 (http://www.scirp.org/journal/epe)
Analysis on the Effect of the Nonlinear Resistance on the
Locomotive Operating Overvoltages
Zhengqing Han, Donglin Zhang, Yuning Wu, Shibin Gao
School of Electrical Engineering, Southwest Jiaotong University, Chengdu, China
Received February, 2013
ABSTRACT
With the application of the articulated phase in sulator, and the speed of electric locomotive rising, it is inev itable for the
electric locomotive to adop t the technolog y automatic passing through the electric phase separation. However, when the
locomotive passes the electric phase separation, a variety of overvoltages will be generated, such as the cut-off over-
voltage and the closing overvoltage. In this paper, the causes of the two overvoltages above are analyzed theoretically
and simulated in Simulink. Then this paper discusses the suppression effects on the cut-off overvoltage and the closing
overvoltage by paralleling th e nonlinear resistance and the main breaker, or parallelling the nonlin ear resistance an d the
locomotive transformer. The simulation resu lts show that parallelling the no nlinear resistance and the locomotive trans-
former has suppressive effects on the two overvo ltages mentioned above.
Keywords: Articulated Phase Insulator; Switching Overvoltage; Nonlinear Resistance; SIMULINK
1. Introduction
The application of the articulated phase insulator can
eliminate the mechanical hard point problem caused by
the device phase separation, and increase the reliability
of the electric locomotive. With the speed rising, the time
interval of passing through the phase separation is re-
duced. When the electric locomotive passes through the
electric phase separation, the traditional approach relies
on the driver’s operation, demoting and closing auxiliary
motor, and disconnecting main breakers in order. After
the locomotive passes, it is then operated in the reverse
order, so the pantograph can pass through phase separa-
tion in the non-current way, ensuring the service life of
the catenary and pantograph [1]. The method is not
adopted in the modern railway system because of its fre-
quent operation and low safety factor, so it becomes a
necessity to use the technology of automatic passing
through the electric ph ase separation (including the vehi-
cle auto-passing phase separation, column auto-passing
phase separation, ground switching auto-passing phase
separation [2]). When the locomotive passes automati-
cally through the ph ase separation, the operation of main
breaker will cause th e cut-off overvo ltage and the clos ing
overvoltage, which are analyzed in literature [3-5]. As
the generated overvoltage threatens the running safety of
locomotive, it is important to find the corresponding
suppressive measures to ensure the safe operation of the
electric locomotive.
This paper analyzes the causes of the cut-off over-
voltage and the closing overvoltage when passing
through the phase separation with adopting the combina-
tion of the ground installations and the column switch.
Literature [6] researched the RC components suppressor.
Literature [1], [6] mentioned th e suppression of no nlinear
resistances, but both were with no simulations. This pa-
per discusses the suppressive effects of the operating
overvoltage by using Matlab.
2. Electric Process Analysis
2.1. The Cut-off Overvoltage
The Figure 1 that can found in [7] shows that the loco-
motive passes through the phase separation with the
combination of the ground installations and the column
switch.
When the electric locomotive passes point A, the main
breaker is automatically disconnected, with the huge
current being cut off which generates arcs. If the inter-
rupters are not strong enough, the electric locomotive
will rush through the phase separation charged, leading
Figure 1. The schematic diagram of electric locomotive
passing the articulated phase insulator.

Z. Q. HAN ET AL.
1244
to the damage of the pantograph and catenary. In severe
2.2. The Closing Overvoltage
the phase separation
According to tracteristics of the traction network
und in [1], an equation
ca
cases, it will result in the traction substation tripped ac-
cident. Otherwise, it will generate high cut-off overvolt-
age.
After the locomotive passes through
to point B, the breaker is required to be closing to resume
power. This operation of the breaker may generate the
closing overvoltage whose peak is related to the catenary
voltage. And locomotive auxiliary winding and asyn-
chronous auxiliary cluster are still in the working state.
Some motors act as the electromotor, while others act as
the generator, so the auxiliary systems can be seen as a
power. The voltage of auxiliary, which is called the re-
sidual voltage, can be coupled to the primary side of the
locomotive transformer, whose peak is related to the
number of auxiliary motors. Due to the presence of re-
sidual voltage, the complete response of the closing cir-
cuit is the superposition of the zero-state response and
the zero-input response, which may increase the peak of
overvoltage, and even lead to the tripped accident of the
traction substation.
3. The Equivalent Circuit of the Overvoltage
3.1. The Equivalent Circuit of Cut-off
Overvoltage
he cha
that the line reactance is much bigger than the resistance,
the intercepting overvo ltag e equivalent circu it is set up as
shown in Figure 2. L1 is the sum of the equivalent reac-
tance of the traction substatio n and the con tact line. C1 is
the circuit equivalent capacitance of the circuit ground.
L2 is the locomotive’s main circuit, while C2 is its
equivalent capacitance to earth.
As seen in Figure 2 that can fo
n be drawn as foll ows .
10
TT
du
C udt
dt L


Namely,
2
2
10
TT
du u
LC
dt  (1)
Assuming that the two initial values are 0
u and '
0
u,
the Equation (1) can be simplified by using Laplace
transform.
 
'
su u
00
1
2TT
Us sL
C

 (2)
Using the inverse transformation of La
pli place to sim- fy the Equation (2),
Figure 2. The equivalent circuit of the intercepti over-
voltage. ng



00 00
'
0
0
'
00000
2' 2
000 0
cos sin /
(/)sin
tjw tjw tjw t
euee
uwtuwtw
uuw wt 

00
1
2
jw
ujwue
jw






 
(3)
where 1/
TT
wLT C and 00
'
0
arctg uw
u
 
Whe is cun the currentt off, it is known that
0mcosuE


and 0msiniI


. Then the conclusion
pacitance voltld not muta t
can be drawn as both the inductive current and the ca-
age coue.
0cos
m
E
u
'
0sin /
/2
1/2
mT
mT
m
NT T
I
C
uEfL
I
fLC























 
(4)

m
K
tion vol
is the ratio of intercepting overvoltage to the trac-
tage.
2
2
0
u
K'2
00 22
(/) cos sin
N
mm
uw f
Ef





 (5)
Because of

,
N
f
f m
K
can be approximately seen as
sin
N
m
f
Kf


 (6) 
From Equation (6), it could be obt
cep
quivalent Circuit of Closing
paration,
ained that the inter-
ting overvoltage is proportional to the circuit reso-
nance frequency and the contact line when the current is
cut down.
3.2. The E
Overvoltage
After the locomotive passes through the phase se
the circuit can be equivalent as shown in Figure 3 for the
moment the switch is on. The p arameters in Figure 3 [8]
are basically the same with the ones in the Fi g ure 2.
In Figure 3, 21 LL and12 CC . Therefore, the
influence of L, C can be ignored, the differen
1tial
equation can be lisollows:
2
ted as f
()
T
du R
RC u
dt L
 udte t (7)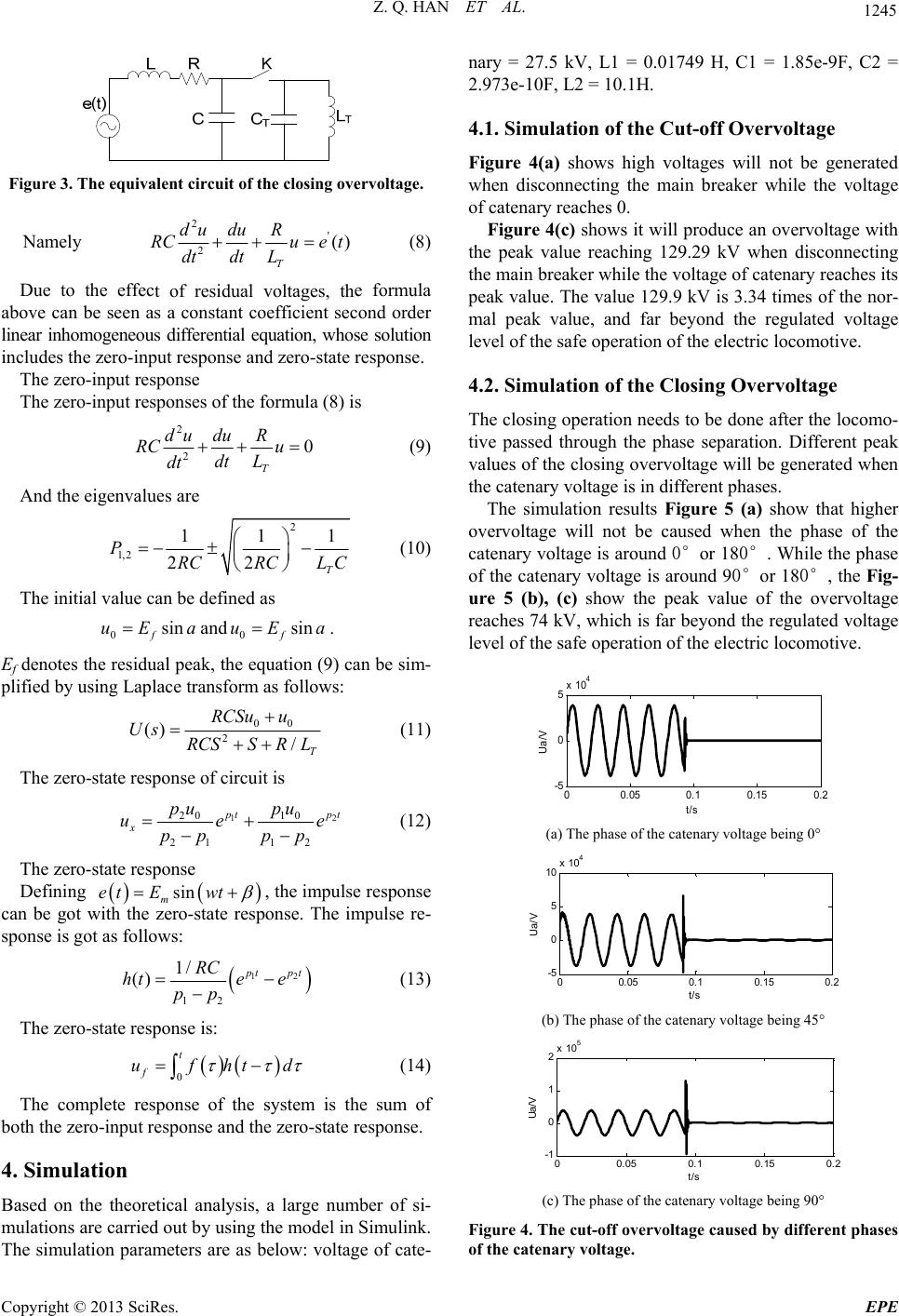

Z. Q. HAN ET AL. 1245
Figure 3. The equivalent circuit of the closing overvoltage.
Namely 2'
2()
du duR
RC ue t (8)
T
dt L dt
t of residual voltages, th
aboves a constant coefficient second order
lin
Due to the effece formula
can be seen a
ear inhomogeneous differential equation, whose solution
includes the zero-input response and zero-state response.
The zero-input response
The zero-input responses of the formula (8) is
2
du
20
T
RC u
dt L dt  
du R (9)
And the eigenvalues are
2
1,2 2
PRC  111
2T RCL C

 

 (10)
The initial value can be defined as
aand a.
Efon (9) can be sim-
plified by using Laplace tr as follows:
0sin f
uE0sin
f
uE
denotes the residual peak, the equati
ansform
00
2
() /T
RCSu u
Us RCSSR L

 (11)
The zero-state response of circuit is
12
20 10
21 12
p
tpt
pupu e
p (12)
The zero-state response
Defining
x
ue
pp p


 
sin
m
et Ewt


e respo
, the impul
can bnse. The impulse re-
sp
se response
e got with the zero-stat
onse is got as follows:

12
1
1/
()
2
p
tpt
RC
hte e
p
 (13)
p
The zero-state response is:
d
 
t
ufht
0
f

 
 (14)
The complete response of the system
both the zero-input response and the zero
Based on the theoretical analysis, a large number of si-
ied out by using the model in Simulink.
The simulation parameters are as below: voltage of cate-
voltages will not be generated
voltage
the voltage of catenary reaches its
pe
o-
peak
when
hile the phase
of
is the sum of
-state response.
4. Simulation
mulations are carr
nary = 27.5 kV, L1 = 0.01749 H, C1 = 1.85e-9F, C2 =
2.973e-10F, L2 = 10.1H.
4.1. Simulation of the Cut-off Overvoltage
Figure 4(a) shows high
when disconnecting the main breaker while the
of catenary r e aches 0.
Figure 4(c) shows it will produce an overvoltage with
the peak value reaching 129.29 kV when disconnecting
the main breaker while
ak value. The value 129.9 kV is 3.34 times of the nor-
mal peak value, and far beyond the regulated voltage
level of the safe operation of the electric locomotive.
4.2. Simulation of the Closing Overvoltage
The closing operation needs to be done after the locom
tive passed through the phase separation. Different
values of th e closing overvoltage will b e generated
the catenary voltage is in different phases.
The simulation results Figure 5 (a) show that higher
overvoltage will not be caused when the phase of the
catenary voltage is around 0°or 180°. W
the catenary voltage is around 90°or 180°, the Fig-
ure 5 (b), (c) show the peak value of the overvoltage
reaches 74 kV, which is far beyond the regulated voltage
level of the safe operation of the electric locomotive.
00.05 0.10.150.2
-5
0
5x 10
4
t/s
Ua/V
(a) The phase of the catenary voltage being 0°
00.05 0.10.15 0.2
-5
0
10 x 10
4
5
t/s
Ua/ V
(b) The phase of the catenary voltage being 45°
00.05 0.10.15 0.2
-1
0
2x 10
5
1
t/s
Ua/ V
(c) The phase of the catenary voltage being 90°
Figure 4. The cut-off overvoltage caused by differen phases
of the catena ry voltage. t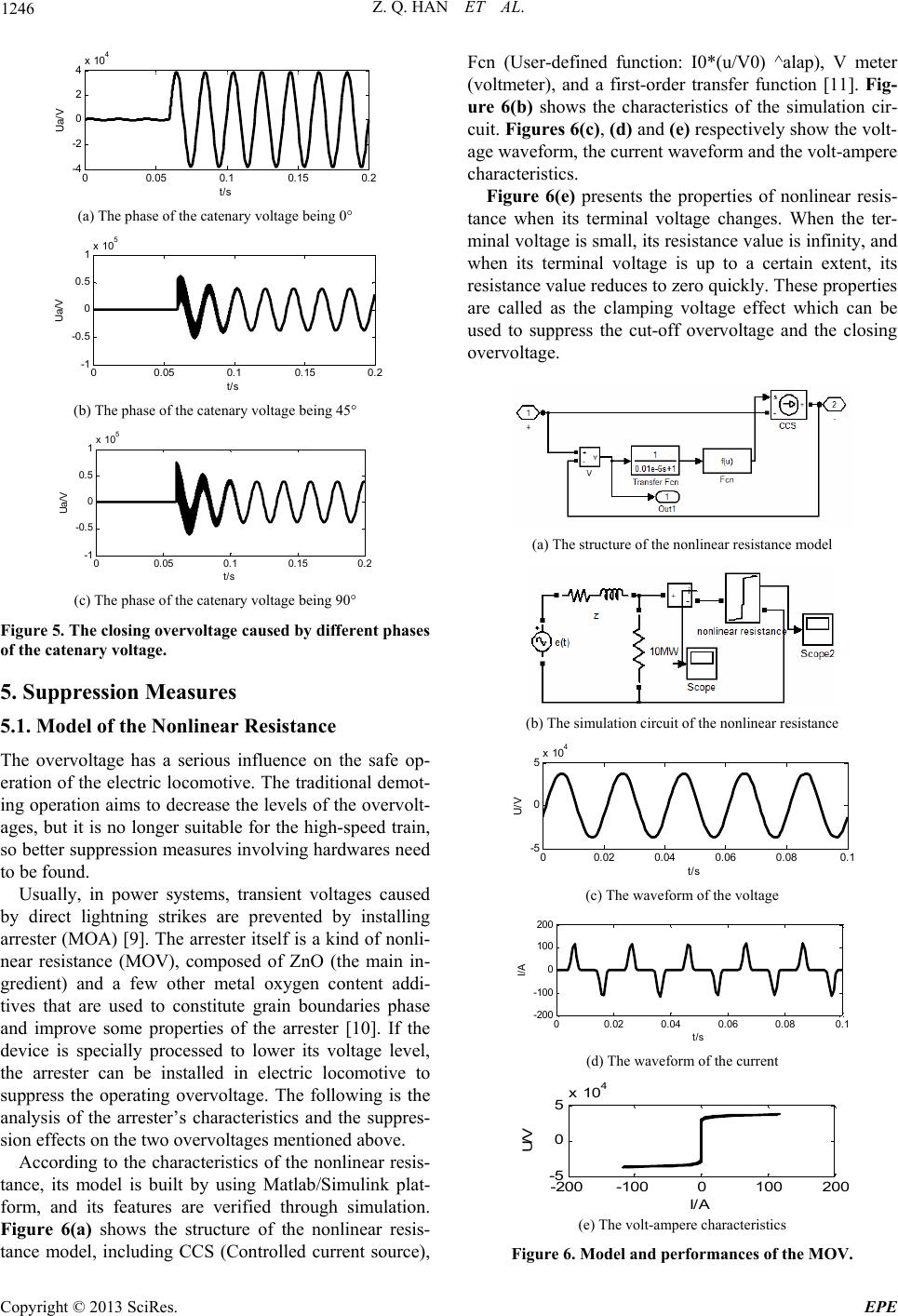

Z. Q. HAN ET AL.
1246
00.05 0.10.15 0.2
-4
-2
0
2
4x 10
4
/V
t/s
Ua
(a) The phase of the catenary voltage being 0°
00.05 0.10.15 0.2
-1
-0. 5
0
0.5
1x 10
5
Ua/V
t/s
(b) The phase of the catenary voltage being 45°
00.05 0.10.15 0.2
-1
-0.5
0
0. 5
1x 10
5
t/s
Ua/V
(c) The phase of the catenary voltage being 90°
Figure 5. The closing overvoltage caused by different phases
of the catena ry voltage.
linear Resistance
fluence on the safe op-
nal demot-
e overvolt-
) [9]. The arrester itself is a kind of nonli-
ne
.
Fi
small, its resistance value is infinity, and
w
5. Suppression Measures
5.1. Model of the Non
The overvoltage has a serious in
eration of the electric locomotive. The traditio
ing operation aims to decrease th e levels of th
ages, but it is no longer suitable for the high-speed train,
so better suppression measures involving hardwares need
to be found.
Usually, in power systems, transient voltages caused
by direct lightning strikes are prevented by installing
arrester (MOA
ar resistance (MOV), composed of ZnO (the main in-
gredient) and a few other metal oxygen content addi-
tives that are used to constitute grain boundaries phase
and improve some properties of the arrester [10]. If the
device is specially processed to lower its voltage level,
the arrester can be installed in electric locomotive to
suppress the operating overvoltage. The following is the
analysis of the arrester’s characteristics and the suppres-
sion effects on the two overvoltages mentioned above.
According to the characteristics of the nonlinear resis-
tance, its model is built by using Matlab/Simulink plat-
form, and its features are verified through simulation
gure 6(a) shows the structure of the nonlinear resis-
tance model, including CCS (Controlled current source),
Fcn (User-defined function: I0*(u/V0) ^alap), V meter
(voltmeter), and a first-order transfer function [11]. Fig-
ure 6(b) shows the characteristics of the simulation cir-
cuit. Figures 6(c), (d) and (e) respectively show the volt-
age waveform, the current waveform and the volt-ampere
characteristics.
Figure 6(e) presents the properties of nonlinear resis-
tance when its terminal voltage changes. When the ter-
minal voltage is
hen its terminal voltage is up to a certain extent, its
resistance value reduces to zero quickly. These properties
are called as the clamping voltage effect which can be
used to suppress the cut-off overvoltage and the closing
overvoltage.
(a) The structure of the nonlinear resistance model
(b) The simulation circuit of the nonlinear resistance
00.02 0.04 0.06 0.08 0.1
-5
0
5x 10
4
U/ V
t/s
(c) The waveform of the voltage
00.02 0.04 0.060.080.1
-200
-100
0
100
200
t/s
I/A
(d) The waveform of the current
-200 -100 0100 200
-5
0
5x 10
4
I/A
U/V
(e) The volt-ampere characteristics
Figure 6. Model and performances of the MOV.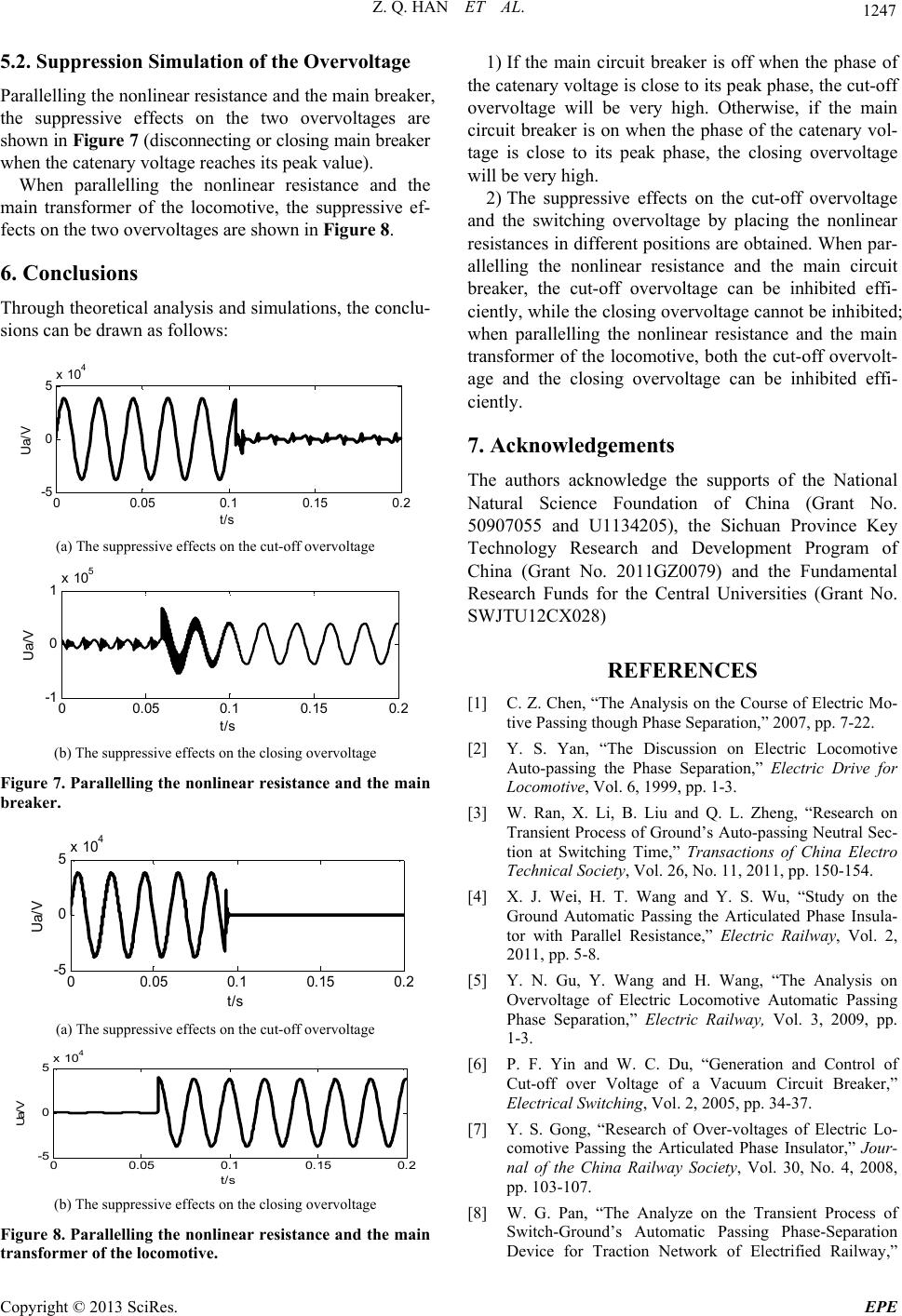

Z. Q. HAN ET AL. 1247
5.2. Suppression Simulation of the Overvoltage
Parallelling the non linear resistance and the main break er,
the suppressive effects on the two overvoltages are
shown in Figure 7 (disconnecting or closing main breaker
when the catenary voltage reaches its peak value).
When paralnce ahe
main transformer ouppressive ef-
fects
lelling the nonlinear resista
f the locomotive, the snd t
on the two overvoltages are shown in Figur e 8.
6. Conclusions
Through theoretical analysis and simulations, the conclu-
sions can be drawn as follows:
00.05 0.10.15 0.2
-5
0
5x 10
4
Ua/ V
t/s
(a) The suppressive effects on the cut-off overvoltage
00.05 0.10.15 0.2
-1
0
1x 10
5
t/s
Ua/V
(b) The suppre ssive effects on the closing overvoltage
Figure 7. Parallelling the nonlinear resistance and the main
breaker.
00.05 0.1 0.15 0.2
-5
0
5x 10
4
Ua/ V
(a) The suppressive effects on the cut-off overvoltage
t/s
00.05 0.1 0.15 0.2
-5
0
5x 10
4
Ua/V
t/s
(b) The suppre ssive effects on the closing overvoltage
Figure e main
transformer of the locomotive.
1) If the main circuit breaker is off when the phase of
the catenary voltage is close to its peak phase, the cut-off
overvoltage will be very high. Otherwise, if the main
circuit breaker is on when the phase of the catenary vol-
tage is close to its peak phase, the closing overvoltage
will be very high.
2) Toltage
X028)
NCES
s of Ground’s Auto-passing Neutral Sec-
tion at Switching Time,” Transactions of China Electro
Technical Soc1, pp. 150-154.
[4] X. J. Wei, H.u, “Study on the
ve Automatic Passing
,”
a Railway Society, Vol. 30, No. 4, 2008,
e for Traction Network of Electrified Railway,”
8. Parallelling the nonlinear resistance and th
pp.
he suppressive effects on the cut-off overv
and the switching overvoltage by placing the nonlinear
resistances in different positions are obtained. When par-
allelling the nonlinear resistance and the main circuit
breaker, the cut-off overvoltage can be inhibited effi-
ciently, while the closing overvo ltage cannot be inhibited;
when parallelling the nonlinear resistance and the main
transformer of the locomotive, both the cut-off overvolt-
age and the closing overvoltage can be inhibited effi-
ciently.
7. Acknowledgements
The authors acknowledge the supports of the National
Natural Science Foundation of China (Grant No.
50907055 and U1134205), the Sichuan Province Key
Technology Research and Development Program of
China (Grant No. 2011GZ0079) and the Fundamental
Research Funds for the Central Universities (Grant No.
SWJTU12C
REFERE
[1] C. Z. Chen, “The Analysis on the Course of Electric Mo-
tive Passing though Phase Separation,” 2007, pp. 7-22.
[2] Y. S. Yan, “The Discussion on Electric Locomotive
Auto-passing the Phase Separation,” Electric Drive for
Locomotive, Vol. 6, 1999, pp. 1-3.
[3] W. Ran, X. Li, B. Liu and Q. L. Zheng, “Research on
Transient Proces
iety, Vol. 26, No. 11, 201
T. Wang and Y. S. W
Ground Automatic Passing the Articulated Phase Insula-
tor with Parallel Resistance,” Electric Railway, Vol. 2,
2011, pp. 5-8.
[5] Y. N. Gu, Y. Wang and H. Wang, “The Analysis on
Overvoltage of Electric Locomoti
Phase Separation,” Electric Railway, Vol. 3, 2009, pp.
1-3.
[6] P. F. Yin and W. C. Du, “Generation and Control of
Cut-off over Voltage of a Vacuum Circuit Breaker
Electrical Switching, Vol. 2, 2005, pp. 34-37.
[7] Y. S. Gong, “Research of Over-voltages of Electric Lo-
comotive Passing the Articulated Phase Insulator,” Jour-
nal of the Chin
103-107.
[8] W. G. Pan, “The Analyze on the Transient Process of
Switch-Ground’s Automatic Passing Phase-Separation
Devic

Z. Q. HAN ET AL.
1248
Lightning
System,” Beijing, Vol. 5, 1997, pp. 74-90. 2008.
[9] Y. L. Wang, D. Y. Zhao and S. H. Hu, “Development
Trends of Line Arresters,” Electrical Porcelain [11
Arrester, Vol. 1, 2011, pp. 26-34.
[10] Y. J. Liang, “Application of Metal Oxide Varistors in
Power
] J. Wang and G. Q. Weng, “MATLAB/SIMULINK
Simulation and Application of Electric Power System,”
Xi’an, 2008, pp. 271-275.