Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 181-188 doi:10.4236/am.2011.22020 Published Online February 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Hyperbolic Fibonacci and Lucas Functions, “Golden” Fibonacci Goniometry, Bodnar’s Geometry, and Hilbert’s Fourth Problem —Part II. A New Geometric Theory of Phyllotaxis (Bodnar’s Geometry) Alexey Stakhov1,2, Samuil Aranson3 1International Higher Education Academy of Sciences, Moscow, Russia 2Institute of the Golden Section, Academy of Trinitarism, Moscow, Russia 3Russian Academy of Natural History, Moscow, Russia E-mail: goldenmuseum@rogers.com, saranson@yahoo.com Received June 25, 201 0; revised November 15, 2010; accepted November 20, 2010 Abstract This article refers to the “Mathematics of Harmony” by Alexey Stakhov in 2009, a new interdisciplinary di- rection of modern science. The main goal of the article is to describe two modern scientific discoveries–New Geometric Theory of Phyllotaxis (Bodnar’s Geometry) and Hilbert’s Fourth Problem based on the Hyper- bolic Fibonacci and Lucas Functions and “Golden” Fibonacci -Goniometry ( is a given positive real number). Although these discoveries refer to different areas of science (mathematics and theoretical botany), however they are based on one and the same scientific ideas-the “golden mean,” which had been introduced by Euclid in his Elements, and its generalization—the “metallic means,” which have been studied recently by Argentinian mathematician Vera Spinadel. The article is a confirmation of interdisciplinary character of the “Mathematics of Harmony”, which originates from Euclid’s Elements. Keywords: Euclid’s Fifth Postulate, Lobachevski’s Geometry, Hyperbolic Geometry, Phyllotaxis, Bodnar’s Geometry, Hilbert’s Fourth Problem, The “Golden” and “Metallic” Means, Binet Formukas, Hyperbolic Fibonacci and Lucas Functions, Gazale Formulas, “Golden” Fibonacci -Goniometry 1. Omnipresent Phyllotaxis 1.1. Examples of Phyllotaxis Objects Everything in Nature is subordinated to stringent mathe- matical laws. Prove to be that leaf’s disposition on plant’s stems also has stringent mathematical regularity and this phenomenon is called phyllotaxis in botany. An essence of phyllotaxis consists in a spiral d isposition of leaves on plant’s stems of trees, petals in flower baskets, seeds in pine cone and sunflower head etc. This phenomenon, known already to Kepler, was a subject of discussion of many scientists, including Leonardo da Vinci, Turi ng, Veil and so on. In phyllotaxis phenomenon more complex concepts of symmetry, in particular, a concept of helical symmetry, are used. The phyllotaxis phenomenon reveals itself especially brightly in inflorescences and densely packed botanical structures such, as pine cones, pineapples, cacti, heads of sunflower and cauliflower and many other objects (Fig- ure 1). On the surfaces of such objects their bio-organs (seeds on the disks of sunflower heads and pine cones etc.) are placed in the form of the left-twisted and right-twisted spirals. For such phyllotaxis objects, it is used usually the number ratios of the left-hand and right-hand spirals ob- served on the surface of the phyllotaxis objects. Botanists proved that these ratios are equal to the ratios of the ad- jacent Fibonacci numbers, that is, 1235813211 5 :,,,, ,, 1235813 2 n n F F (2.1) The ratios (2.1) are called phyllotaxis orders. They are different for different phyllotaxis objects. For example, a head of sunflower can have the phyllotaxis orders given by Fibonacci’s ratios 89 144 , 5589 and even 233 144 .  A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 182 (a) (b) (c) (d) (e) (f) Figure 1. Phyllotaxis structures: (а) cactus; (b) head of sunflower; (c) coneflower; (d) romanescue cauhflower; (e) pineapple; (f) pinecone. Geometric models of phyllotaxis structures in Figure 2 give more clear representation about this unique bo- tanical phenomenon. 1.2. Puzzle of Phyllotaxis By observing the subj ects of ph yllotax is in th e co mpleted form and by enjoying the well organized picture on its surface, we always ask a question: how are Fibonacci’s spirals forming on its surface during its growth? It is pro- ved that a majority of bio-forms changes their phyllo- taxis orders during their growth. It is known, for example, that sunflower disks located on the different levels of the same stalk have the different phyllotaxis orders; more- over, the more an age of the disk, the more its phyllotaxis order. This means that during the growth of the phyllo- taxis subject, a natural modification (an increase) of sym- metry happens and this modification of symmetry obeys the law: 23581321 12358 13 (2.2) The modification of the phyllotaxis orders according to (2.2) is named dynamic symmetry [1]. All the above data are the essence of the well known “puzzle of phyllo- taxis”. Many scientists, who investigated this problem, did believe what the phenomenon of the dynamical sym- metry (2.2) is of fundamental interdisciplinary impor- tance. In opinion of Vladimir Vernadsky, the famous Russian scientist-encyclopedist, a problem of biological symmetry is the key problem of biology. Thus, the phenomenon of the dynamic symmetry (2.2) plays a special role in the geometric problem of phyllo- taxis. One may assume that the numerical regularity (2.2) reflects some general geometric laws, which hide a secret of the dynamic mechanism of phyllotaxis, and their un- covering would be of great importance for understanding the phyllotaxis phenomenon in the whole. A new geometric theory of phyllotaxis was developed recently by Ukrainian architect Oleg Bodnar. This origi- nal theory is stated in Bodnar’s book [1]. 2. Bodnar’s Geometry 2.1. Structural-Numerical Analysis of Phyllotaxis Lattices Let’s consider the basic ideas and concepts of Bodnar’s geometry [1]. We can see in Figure 3(a) a cedar cone as characteristic example of phyllotaxis subject. On the surface of the cedar cone its each seed is blocked with the adjacent seeds in three directions. As the outcome 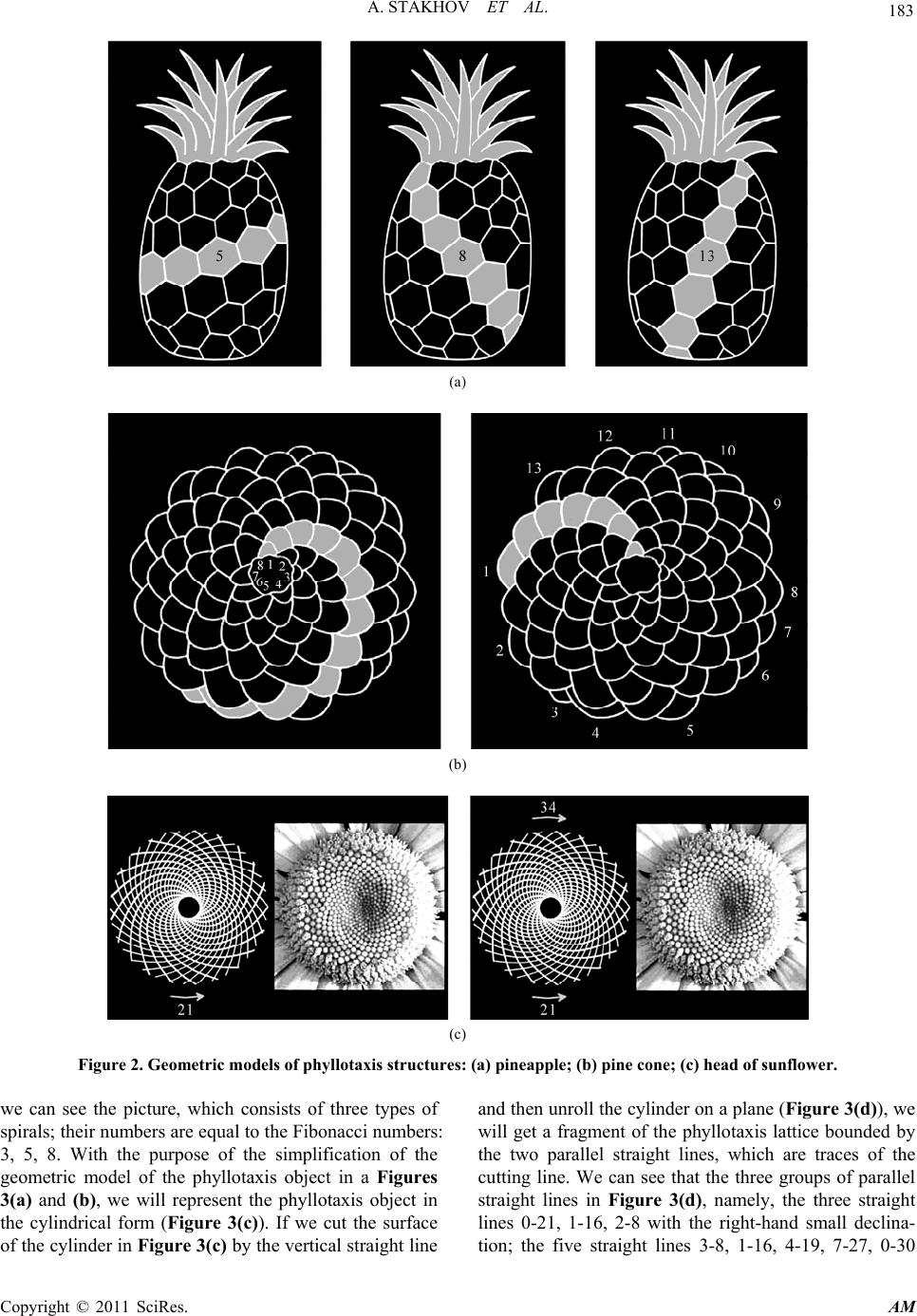 A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 183 (a) (b) (c) Figure 2. Geometric models of phyllotaxis structures: (а) pineapple; (b) pine cone; (c) head of sunflower. we can see the picture, which consists of three types of spirals; their numbers are equal to the Fibonacci numbers: 3, 5, 8. With the purpose of the simplification of the geometric model of the phyllotaxis object in a Figures 3(a) and (b), we will represent the phyllotaxis object in the cylindrical form (Figure 3(c)). If we cut the surface of the cylinder in Figure 3(c) by the vertical straight line and then unroll th e cylinder on a p lane (Figure 3(d)), we will get a fragment of the phyllotaxis lattice bounded by the two parallel straight lines, which are traces of the cutting line. We can see that the three groups of parallel straight lines in Figure 3(d), namely, the three straight lines 0-21, 1-16, 2-8 with the right-hand small declina- tion; the five straight lines 3-8, 1-16, 4-19, 7-27, 0-30 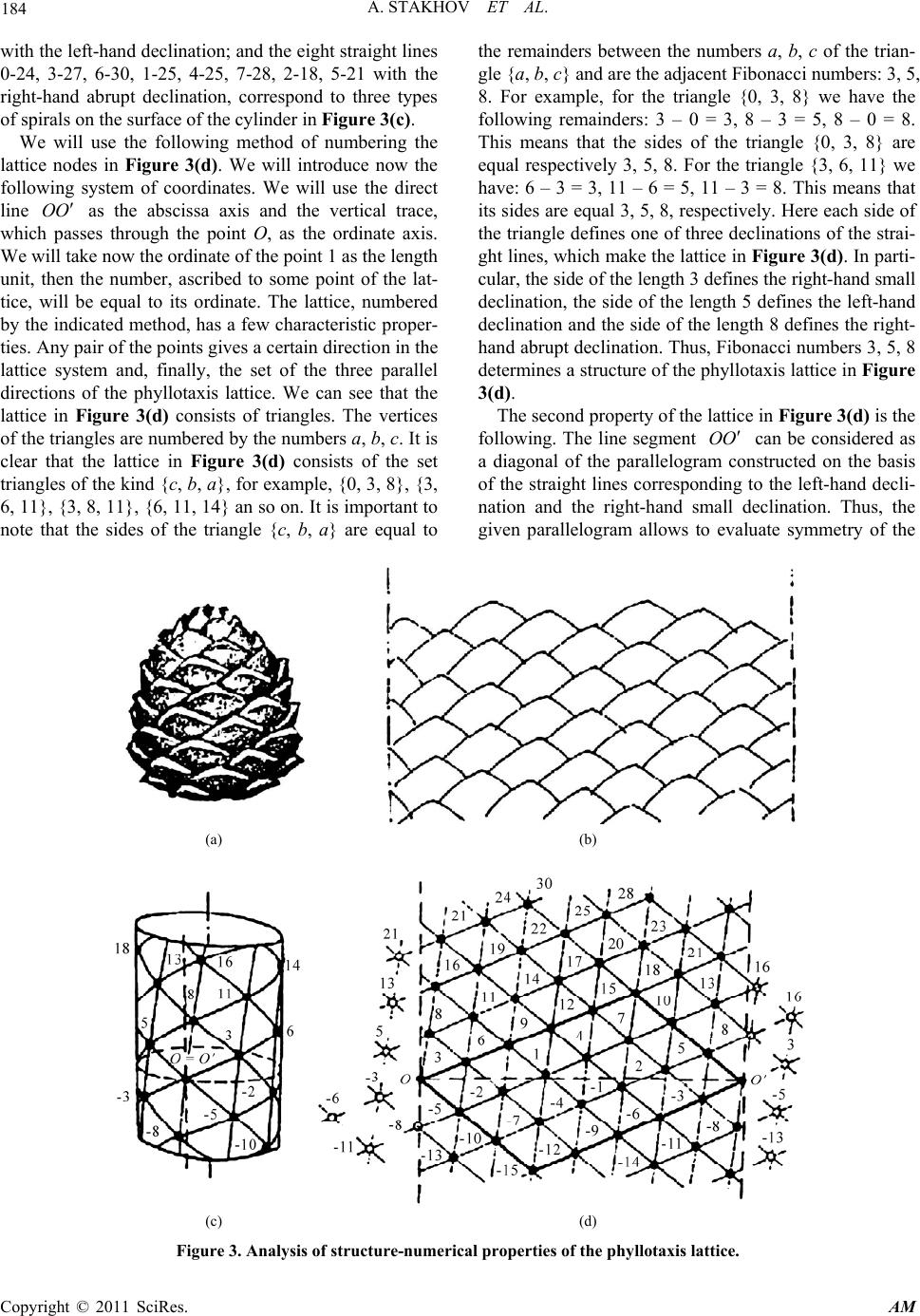 A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 184 with the left-hand declin ation; and the eight straig ht lines 0-24, 3-27, 6-30, 1-25, 4-25, 7-28, 2-18, 5-21 with the right-hand abrupt declination, correspond to three types of spirals on the surface of the cylinder in Figure 3(c). We will use the following method of numbering the lattice nodes in Figure 3(d). We will introduce now the following system of coordinates. We will use the direct line OO as the abscissa axis and the vertical trace, which passes through the point O, as the ordinate axis. We will take now the ordinate of the point 1 as the leng th unit, then the number, ascribed to some point of the lat- tice, will be equal to its ordinate. The lattice, numbered by the indicated method, has a few characteristic proper- ties. Any pair of the points gives a certain direction in the lattice system and, finally, the set of the three parallel directions of the phyllotaxis lattice. We can see that the lattice in Figure 3(d) consists of triangles. The vertices of the triangles are numbered by the numbers a, b, c. It is clear that the lattice in Figure 3(d) consists of the set triangles of the kind {c, b, a}, for example, {0, 3, 8}, {3, 6, 11}, {3, 8, 11}, {6, 11, 14} an so on. It is important to note that the sides of the triangle {c, b, a} are equal to the remainders between the numbers a, b, c of the trian- gle {a, b, c} and are the adjacent Fibonacci numbers: 3, 5, 8. For example, for the triangle {0, 3, 8} we have the following remainders: 3 – 0 = 3, 8 – 3 = 5, 8 – 0 = 8. This means that the sides of the triangle {0, 3, 8} are equal respectively 3, 5, 8. For the triangle {3, 6, 11} we have: 6 – 3 = 3, 11 – 6 = 5, 11 – 3 = 8. This means that its sides are equal 3, 5, 8, respectively. Here each side of the triangle defines one of three declinations o f the strai- ght lines, which make th e lattice in Figure 3(d). In parti- cular, the side of the length 3 defines the right-hand small declination, the side of the length 5 defines the left-hand declination and the side of the length 8 defines the right- hand abrupt declination. Thus, Fibonacci numbers 3, 5, 8 determines a structure of the phyllotaxis lattice in Figure 3(d). The second property of th e lattice in Figure 3(d) is the following. The line segment OO can be considered as a diagonal of the parallelogram constructed on the basis of the straight lines corresponding to the left-hand decli- nation and the right-hand small declination. Thus, the given parallelogram allows to evaluate symmetry of the (a) (b) (c) (d) Figure 3. Analysis of structure-numerical properties of the phyllotaxis lattice.  A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 185 lattice without the use of digital numbering. We will name this parallelogram by coordinate parallelogram. Note that the coordinate parallelograms of different sizes correspond to the lattices with different symmetry. 2.2. Dynamic Symmetry of the Phyllotaxis Object We will start the analysis of the phenomenon of dynamic symmetry. The idea of the analysis consists of the com- parison of the series of the phyllotaxis lattices (th e unrol- ling of the cylindrical lattice) with different symmetry (Figure 4). In Figure 4 the variant of Fibonacci’s phyllotaxis is illustrated, when we observe the following modification of the dynamic symmetry of the phyllotaxis object dur- ing its growth: 1:2:1 2:3:1 2:5:3 5:8:3 5:13:8. Note that the lattices, represented in Figure 4, are con- sidered as the sequential stages (5 stages) of the trans- formation of one and the same phyllotaxis object during its grows. There is a question: how are carrying out the transformations of the lattices, that is, which geometric movement can be used to provide the sequential passing all the illustrated stages of the phyllotaxis lattice? 2.3. The Key Idea of Bodnar’s Geometry We will not go deep into Bodnar’s original reasoning’s, which resulted him in a new geometrical theory of phyl- lotaxis, and we send the readers to the remarkable Bod- nar’s book [1] for more detailed acquaintance with his original geometry. We will turn our attention only to two key ideas, which underlie this geometry. Now we will begin from the analysis of the phenome- non of dynamic symmetry. The idea of the analysis con- sists of the comparison of the series of the phyllotaxis lattices of different symmetry (Figure 4). We will start from the comparison of the stages I and II. At these sta- ges the lattice can be transformed by the compression of the plane along the direction 0-3 up to the position, wh en the line segment 0-3 attains the edge of the lattice. Si- multaneously the expansion of the plane in the direction 1-2, perpendicular to the compression direction, should happen. At the passing on from the stage II to the stage III, the compression should be made along the direction О-5 and the expansion along the perpendicular direction 2-3. The next passage is accompanied by the similar de- formations of the plane in the direction О-8 (compres- sion) and in the perpendicular direction 3-5 (expansion). But we know that the compression of a plane to any straight line with the coefficient k and the simultaneous expansion of a plane in the perpendicular direction with the same coefficient k are nothing as hyperbolic rotation [2]. A scheme of hyperbolic transformation of the lattice fragment is presented in Figure 5. The scheme corres- ponds to the stage II of Figure 4. Note that the hyperbola of the first quadrant has the equation xy = 1, and the hy- perbola of the fourth quadrant has the equation xy = –1. Figure 4. Analysis of the dynamic symmetry of phyllotaxis object.  A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 186 It follows from this consideration the first key idea of Bodnar’s geometry: the transformation of the phyllotaxis lattice in the process o f its growth is carried out b y means of the hyperbolic rotation, the main geometric transfor- mation of hyperbolic geometry. This transformation is accompanied by a modification of dynamic symmetry, which can be simulated by the se- quential passage from the object with the smaller sym- metry order to the object with the larger symmetry order. However, this idea does not give the answer to the question: why the phyllotaxis lattices in Figure 4 are based on Fibonacci numbers? 2.4. The “Golden” Hyperbolic Functions For more detail study of the metric properties of the lat- tice in Figure 5 we will consider its fragment repre- sented in Figure 6. Here the disposition of the points is similar to Figure 5. Let us note the ba sic peculiarities of the dispo sition of the points in Figure 6: 1) the points М1 and М2 are symmetrical regarding to the bisector of the right angle YOX; 2) the geometric figures OM1M2N1, OM2N2N1, OM2M3N2 are parallelograms; 3) the point А is the vertex of the hyperbola yx = 1, that is, xA = 1, yA = 1, therefore 2OA . Let us evaluate the abscissa of point M2 denoted 2 M x x . Taking into consideration a symmetry of the points M1 and M2, we can write: 1 1 M x x . It follows from the symmetry condition of these points what the line segment M1M2 is tilted to the coordinate axises un- der the angle of 45˚. The line segment M1M2 is parallel to the line segment ОN1; this means that the line segment ОN1 is tilted to the coordinate axises under the angle of 45˚. Therefore, the point N1 is a top of the lower branch of the hyperbola; here 11 N x, 11 N y, 12ON OA. It is clear that 112 2ONM M. And now it is ob- vious, what the remainder between the abscissas of the points M1 and M2 is equal to 1. These considerations resulted us in the following equ- ation for the calculation of the abscissa of the point M2, that is, 2 M x x: 12 1or 10,xxx x (2.3) This means that the abscissa 2 M x x is a positive root of the famous “golden” algebraic equation: 2 15 2 M x . (2.4) Thus, a study of the metric properties of the phyllo- taxis lattice in Figures 5 and 6 unexpectedly resulted in Figure 5. A general scheme of the phyllotaxis lattice trans- formation in the system of the equatorial hyperboles. 2 2 Figure 6. The analysis of the metric properties of the phyl- lotaxis lattice. the golden mean. And this fact is the second key outcome of Bodnar’s geometry. This result was used by Bodnar for the detailed study of phyllotaxis phenomenon. By developing this idea, Bodnar concluded that for the ma- thematical simulation of phyllotaxis phenomenon we need to use a special class of the hyperbolic functions, named “golden” hyperbolic functions [1]:  A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 187 The “golden” hyperbolic sine 2 nn Gshn (2.5) The “golden” hyperbolic cosine 2 nn Gchn (2.6) In further, Bodnar found a fundamental connection of the “golden” hyperbolic functions with Fibonacci num- bers: 2 21 21 5 Fk Gchk ; (2.7) 2 22 5 F kGshk. (2.8) By using the correlations (2.7), (2.8), Bodnar gave very simple explanation of the “puzzle of phyllotaxis”: why Fibonacci numbers occur with such persistent con- stancy on the surface of phyllotaxis objects. The main reason consists in the fact that the geometry of the “Alive Nature”, in particular, geometry of phyllotaxis is a non- Euclidean geometry; but this geometry differs substan- tially from Lobachevsky’s geometry and Minkovsky’s four-dimensional world based on the classical hyperbolic functions. This difference consists of the fact that the main correlations of this geometry are describ ed with the help of the “golden” hyperbolic functions (2.5) and (2.6) connected with the Fibonacci numbers by the simple correlations (2.7) and (2.8). It is important to emphasize that Bodnar’s model of the dynamic symmetry of phyllotaxis object illustrated by Figure 4 is confirmed brilliantly by real phyllotaxis pictures of botanic objects (see, for example, Figures 1 and 2). 2.5. Connection of Bodnar’s “Golden” Hyperbolic Functions with the Hyperbolic Fibonacci and Lucas Functions By comparing the expressions for the symmetric hyper- bolic Fibonacci and Lucas sine’s and cosines [3] given by the formulas Symmetric hyperbolic Fibonacci sine and cosine , 55 x xxx sFs xcFsx (2.9) Symmetric hyperbolic Lucas sine and cosine x x sLs x ; x x cLs x (2.10) with the expressions for Bodnar’s “golden” hyperbolic functions given by the Formulas (2.5), (2.6), we can find the following simple correlations between the indicated groups of the formulas: 5 2 Gsh xsFsx (2.11) 5 2 Gch xcFsx (2.12) 2Gsh xsFsx (2.13) 2Gsh xcFsx (2.14) The analysis of these correlations allows to conclude that the “golden” hyperbolic sine and cosine introduced by Oleg Bodnar [1] and the symmetric hyperbolic Fibo- nacci and Lucas sine’s and cosines, introduced by Stak- hov and Rozin in [3], coincide within constant factors. A question of the use of the “golden” hyperbolic functions or the hyperbolic Fibonacci and Lucas functions for the simulation of phyllo taxis objects has not a particular sig- nificance because the final result will be the same: al- ways it will result in the unexpected appearance of the Fibonacci or Lucas numbers on the surfaces of phyllo- taxis objects. Concluding Part II of this article, we emphasize a sig- nificance of Bodnar’s geometry for modern theoretical natural sciences: 1) Bodnar’s geometry discovered for us a new “hy- perbolic world”—the world of phyllotaxis and its geo- metric secrets. The main feature of this world is the fact that the basic mathematical properties of this world are described with the hyperbolic Fibonacci and Lucas func- tions, which are a reason of the appearance of Fibonacci and Lucas numbers on the surface of phyllotaxis objects. 2) It is important to emphasize that the hyperbolic Fi- bonacci and Lucas functions, introduced in [3,4], are “natural” functions of Nature. They show themselves in different botanical structures such, as pine cones, pine- apples, cacti, heads of sunflower and so on. 3) As is shown in Part I, the hyperbolic Fibonacci and Lucas functions, based on the golden mean, are a partial case of more general class of hyperbolic functions–the hyperbolic Fibonacci and Lucas -functions ( > 0 is a given real number), based on the metallic means. As Bodnar proves in [1], the hyperbolic Fibonacci and Lu- cas functions underlie a new “hyperbolic world”—the world of phyllotaxis phenomenon. In this connection , we can bring an attention of theoretical natural sciences to the question to search new hyperbolic worlds of Nature, based on the hyperbolic Fibonacci and Lucas -functions. This idea can lead to new scientific discoveries. 3. References [1] O. Y. Bodnar, “The Golden Section and Non-Euclidean  A. STAKHOV ET AL. Copyright © 2011 SciRes. AM 188 Geometry in Nature and Art,” In Russian, Svit, Lvov, 1994. [2] V. G. Shervatov, “Hyperbolic Functions,” In Russian Fizmatgiz, Moscow, 1958. [3] A. P. Stakhov and B. N. Rozin, “On a New Class of Hyperbolic Function,” Chaos, Solitons & Fractals, Vol. 23, No. 2, 2004, pp. 379-389. doi:10.1016/j.chaos.2004.04.022 [4] A. P. Stakhov and I. S. Tkachenko, “Hyperbolic Fibonac- ci Trigonometry,” Reports of the National Academy of Sciences of Ukraine, In Russian, Vol. 208, No. 7, 1993, pp. 9-14. |

