Paper Menu >>
Journal Menu >>
 Applied Mathematics, 2011, 2, 145-154 doi:10.4236/am.2011.22017 Published Online February 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM 145 G-Type Seismic Wave in Magnetoelastic Monoclinic Layer Amares Chattopadhyay, Shishir Gupta, Abhishek K. Singh, Sanjeev A. Sahu Department of Ap pl i e d Mat hematics, Indian School of Mines, Dhanbad, India E-mail: amares.c@gmail.com Received July 15, 201 0; revised October 28, 2010; accepted November 2, 2010 Abstract This paper deals with the study of propagation of G type waves along the plane surface at the interface of two different types of media. The upper medium is taken as monoclinic magnetoelastic layer whereas the lower half-space is inhomogeneous isotropic. Dispersion equation and condition for maximum energy flow near the surface are obtained in compact form. The dispersion equation is in assertion with the classical Love-type wave equation for the isotropic case. Effect of magnetic field and inhomogeneity on phase veloc- ity and variation of group velocity with scaled wave number has been depicted by means of graphs. It is ob- served that inhomogenetity decreases phase velocity and the magnetic field has the favouring effect. A com- parative study for the case of isotropic layer and monoclinic layer over the same isotropic inhomogeneous half space has been made through graphs. Keywords: G-Waves, Magnetoelastic, Dispersion Equation, Monoclinic, Transform Technique 1. Introduction Horizontally polarized surface wave of shear type is known as G-type wave after B. Gutenberg [1-2], who established the existence of a low velocity layer in the earth mantle. It has been studied by researchers that such waves propagate with a group velocity of 4.4 km/s [3-5] and since the group velocity of Love waves over the pe- riod range from about 40 to 300 s is same, so on other hand Love waves with long periods (60 to 300 s) may also be recognized as G-waves. These waves are fol- lowed by dispersed Love waves, especially for continen- tal paths and they exhibit a transient pulse-like character in record. A sequence of G-waves may be observed after a large earthquake. An outstanding case of well devel- oped G-type waves was provided by the earthquake in Peru (January, 1960). Bath and Arroyo [6] presented the result obtained from this earthquake, especially with re- gard to absorption and velocity dispersion of G-waves. Aki [7] discussed the generation and propagation of G- waves from the Niigata earthquake of June 16, 1964. Some other notable works in this field are done by Jef- freys [8], Bhattacharya [9], Chattopadhyay [10], Haskell [11] and others. Possibility of generation of G-waves in different medium has been investigated by different au- thors. Mal [12] studied the generation of G-waves taking the medium to be isotropic. The wave propagation in crystalline media plays a very interesting role in geophy- sics and also in ultrasonic and signal processing. Chat- topadhyay and Keshri [13] presented the low velocity layer by assuming the law of va riation in the lower semi- infinite anisotropic medium of two different media of monoclinic symmetry. Recently, Chattopadhyay et al. [14] discussed the dispersion of G-type waves in low velocity layer. The variation for the half-space in elastic constants and density reduces the equation of motion into Hill’s equation with periodic coefficients which is solved by the method given by Valeev [15]. Valeev considered a certain class of system of linear differential equations with periodic coefficients which have the property that, by means of Laplace transformation, they may be con- verted to a system of linear difference equations, which in turn may be solved by the method of infinite determi- nants. This method of solving Hill’s differential equation has been successfully employed by Bhattacharya [9], Mal [12] and Chattopadhyay [10]. Theoretical and experimental studies regarding to bet- ter understanding of the real earth has led a need for more realistic representation of the medium thro ugh which sei- smic waves propagate. The pr op agatio n of seis mic wave s is affected by the elastic properties of the layered materi- als. Moreover, the materials of the layer might be mag- netoelastic in nature and th e interplay of electromagnetic field with the motion of a deformable solid has its impor- tance in various fields of science and technology. In the present paper we study of the propagation of G  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 146 type waves along the plane surface at the interface of two different types of media. The upper medium is taken as monoclinic magnetoelastic layer whereas the lower half- space is inhomogeneous isotropic. Keeping terms up to first order, the Laplace transform of the displacement is obtained. Dispersion equation and condition for maxi- mum energy flow near the surface are obtained in com- pact form. The dispersion equation is in assertion with the classical Love-type wave equation for the isotropic case. Effect of magnetic field and inhomogeneity on phase velocity and variation of group velocity with scaled wave number has been depicted by means of graphs. It is observed that inhomogenetity decreases phase velocity and the magnetic field has the favouring effect. A com- parative study for the case of isotropic layer and mono- clinic layer over the same isotropic inhomogeneous half space has bee n made through graphs. The formulation part and solution part of the problem has been dealt in Section 2. In the same section disper- sion equation, the condition for maximum energy flow near the surface and the expression for group velocity have been obtained. Special cases for the dispersion equation obtained in Section 2 are considered in Section 3. Section 4 deals with the numerical calculation and gra- phical illustratio n for the problem. Finally, Section 5 con- cludes the study. 2. Formulation and Solution of the Problem We consider a monoclinic magnetoelastic layer of thick- ness H lying over an inhomogeneous isotropic half-space. The variation for half-space is taken in following manner 20 20 1cos 1cos s y s y (1) where is small positive con stant and s is real depth parameter. The axes Z and Y are taken horizontally and vertically downwards respectively (Figure 1). At first, we deduce the equation governing the propa- gation of shear wave in monoclinic magnetoelastic crus- tal layer. The strain-displacement relations for monoclinic me- dium are 123 4 56 ,,, , , uvwwv SSS S x yzyz uw vu SS zx xy (2) where ,,uvw are displacement components in the di- rection x, y, z respectively, and 1, 2,, 6 i Si are the strain components. Also, the stress-strain relation for a rotated y-cut quartz Monoclinic Magnetoela s t ic medi um Z Y H O 66 56 55 ,,,CCC 20 1cos s y 20 1cos s y Inhomogeneous Isotropic half-space Figure 1. Geometry of the problem. plate, which exhibits monoclinic symmetry with x being the diagonal axis are 111 1122133144 212122 223324 4 313 1232333344 414124 234344 4 555 556 6 656 5666 , , , , , TCSCSCSCS TCSCSCSCS TCSCSCSCS TCSCSCSCS TCSCS TCSCS (3) where 1, 2,, 6 i Ti are the stress components and 1, 2,, 6 ij ji CCi are the elastic constants. Equations governing the propagation of small elastic disturbances in a perfectly conducting monoclinic me- dium having electromagnetic force JB (the Lorentz force, J being the electric current density and B be- ing the magnetic induction vector) as the only body for- ces are 2 65 12 2 624 2 2 53 42 , , x y z TT Tu JB xyz t TTT v JB xyz t TT Tw JB xyz t (4) where is the density o f the layer. For SH wave propagating in the z-direction and caus- ing displacement in the x-direction only, we shall assume that ,, ,0and0.uuyztvw x (5) Using Equations (2) and (5), the stress-strain relation (3) becomes  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 147 1234 55556 65666 0, , . TTTT uu TCC zy uu TC C zy (6) Using Equation (6) in Equation (4), the only non-vani- shing equati on we h ave 222 2 6656 55 222 2. x uuu u CCCJB yz yzt (7) The well known Maxwell’s equations governing the electromagnetic field are 0, , with , e t t B BE HJ u BHJ EB (8) where E is the induced electric field, J is the current density vector and magnetic field H includes both pri- mary and induced magnetic fields. e and are the induced permeability and conduction coefficient respec- tively. The linearized Maxwell’s stress tensor 0x M ij due to the magnetic field is given by 0x M ijeijj ikkij HhHh Hh . Let 123 ,, ,,, H HH uvwHu and 123 ,, i hhhh where i h is the change in the magnetic field. In writing the above equations, we have neglected the displacement current. From Equation (8), we get 2. ett Hu HH (9) In component form, Equation (9) can be written as 23 2 11 2 22 2 33 1, 1, 1. e e e uu HH Htt H tyz HH t HH t (10) For perfectly conducting medium i.e. , the Equation (10) beco mes 3 20, H H tt (11) and 23 1. uu HH Htt ty z (12) It is clear from Equation (11) that there is no perturba- tion in 2 H and 3 H , however from Equation (12) there may be perturbation in 1 H . Therefore, taking small per- turbation, say 1 h in 1 H , we have 1011 H Hh , 202 H H and 303 H H , where 01 0203 ,,HHH are components of the initial magnetic field 0 H. We can write 000 0,sin ,cosHH H, where 00 HH and is the angle at which the wave crosses the m agneti c fi el d. Th us we have 10 0 ,sin,coshH H H (13) We shall take initial value of 1 h as 10h . Using Equation (13) in Equation (12), we get 00 1 sin cos . uu HH htt ty z (14) Integrating with respect to t, we get 10 0 sincos . uu hH H yz (15) Considering 2 2 H HHHH and Equation (8), we get 2. 2 eH JBH H (16) In the component form Equation (16) can be written as 222 22 2 022 0and sinsin 2cos. yz e x uuu Hyz yz JB JB JB (17) Using Equations (7) and (17), we find the equation of motion for the magnetoelastic monoclinic medium in the form 2222 6656 55 222 2. uuuu MMM yz yzt (18) where 2 66 66 2 55 5566 66 56 5666 66 1sin, cos , cos sin H H H MC m C MC m C C MC m C (19) where 2 0 66 e H H mC is monoclinic-magnetoelastic cou- pling parameter.  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 148 Hence, the equation of motion for the propagation of shear wave in monoclinic magnetoelastic crustal layer is 2222 6656 55 222 2. uuuu MMM yz yzt (20) Now we consi der 11 ,, ik zct uyztUye (21) where k is wave number and c is wave velocity. Substituting Equation (21) in Equation (20), we get 222 11 665655 1 220 dU dU MikMkcMU dy dy . (22) Solution of Equation (22 ) is 2 1cos sin y Uy eAPyBPy (23) where 2 2 2 5655 56 6666 6666 2, ikMM kkM P MMMM and , A B are constants. Since the upper surface is stress free therefore, 11 6656 0 uu MM yz at y H , gives 2 1 1666656 sin cos sin 2 y UybeMPyH MPPyH ikMPyH (24) In lower inhomogeneous half-space the displacement 2,,uyzt satisfy the differential equation 2 222 000 2 1cos1cos 1cos uuu sysy sy zzyy t (25) we considered 22 ,, ik zct uyzt Uye (26) Using (25) and (26), the equation of motion for lower inhomogeneous medium may be written as 22 22 2 0222 22 22 0 2 22 2222 00 22 222 2 00 2222 0. 2222 isy isy dUdU dU is ekcUykUy dy dy dy dU dU is kckU yekcUykU ydy dy (27) This is Hill’s different ial equation, which we will so lve by the method given by Valeev [15]. We apply Laplace transform with respect to y, i.e. we multiply (27) by p y e and integrate with respect to y from 0 to , we get 2 222 022 22 2 0 0 2 22 2 022 22 2 0 0 222 2 0 22 20 0 2222 2222 0. pisy pisy py dU dU is ekcUykUy dy dy dy dU dU is ekcUykUy dy dy dy dU ekckUydy dy (28) Now the boundary conditions are 12 112 6656 2 11 66 56 (i)at 0 (ii)at 0 (iii)0 at. uu y uuu MM y yzy uu MM yH yz (29) From (i) of Equation (29) we get 66 21 5666 0sincos 2 M UbikM PHMPPH (30) Now we consi der 2 0 0 y dU qdy and (0) 20 1. Then (ii) of Equation (29 ) gives  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 149 66 166 5666 0 2 66 66 566656 5666 0sincos 22 cos sinsincos 22 M b qMikM PHPMPH MM PikMPH PMPHikMikMPH PMPH (31) Now defining the Laplace transform of 2 Uy as 2 0 py F peUydy . (32) Using the boundary conditions we obtain the following system of equations 2 22 2 0 0 2 22 2 0 0 22 12 222 2 222 2 is kckpispis Fpis is kckpispis Fpis pwFpp (33) where 122 22 2 0 0 10,10 and 1 Vq wk c (34) To find F p from Equation (33), we replace p by pism and divide throughout by n ism , 0m . We then obtain the following infinite system of linear algebraic equations in the quantities F pism, 0, 1, 2,m 2 22 2 0 0 22 2 22 2 0 0 12 111 222 2 111 222 2 n n n n is ismkc kpismpismFpism ismpismwFp ism is ismkckpis mpis mFpis m ismp ism (35) where p may be c onside red as a para meter in th e coef- ficients. It should be noted that in order not to have to consider the special case 0m separately, we include Equation (33) in (35) by agreeing to regard 1 n ism when 0m. Solving the system of difference Equation (35), we obtain F p as the ratio of two infinite de- terminants, viz. 1 2 Fp (36) where 2212 22 222 2 0 0 0 0 112 2 2 22 12 0 22 22 22 22 0 nn nn ispis wispis kc kkc k P is is p isp isp isp is is pisis pisw  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 150 and 222222 0 0 22 222 2 0 0 22 0 0 22 2 2 22 222 0 0 0 2222 22 22 22 22 02222 nn nn is ispiswisk ckpp kc kkc k pw is is p isp isp isp is is isk ckppispisw The first approximation of Equation (36) is 12 12 2222 022 2 11pBB p FP pw pwpw (37) where 66 1 15666 sin cos 2 M BbikMPHPMPH and 66 66 2 16656665666 66 56 5666 sincoscos sin 22 2 sincos . 2 MM Bb MikMPHPMPHPikMPHPMPH M ikMikMPH PMPH The second approximation of Equation (36) is 3 4 Fp (38) where 2212 22 222 2 0 0 0 0 312 2 2 22 12 0 22 22 22 22 0 nn nn ispiswisp is kc kkc k P is is p isp ispisp is is pisis pisw and 222222 0 0 22 222 2 0 0 22 0 0 42 2 2 22 222 0 0 0 2222 22 22 22 22 02222 nn nn is ispiswisk ckpp kc kkc k pw is is p isp isp isp is is isk ckppispisw  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 151 Neglecting the terms containing 2 an d hi gher powers , we g e t 22 22222 0 312 0 22 22 12 22 2222 0 12 0 222 2 222 2 nis sppisw kckpispis ppis wpis w is p ispiswkckpispis and 22 222 2 2 4. n s pwpiswpisw Hence Equation (38) becomes 2 222 2 0 12 22 2 2220 2 2222 0 2 222 0 00 2 00 2 Vpisq p F Pkckpisispis pw pwpis w Vpisq kckp isispis pwpis w (39) Then 2 Uy will be obtained from the following in- version formula: 21 2 ipy i Uy Fpedp (40) The residues 123 ,,RRR at the poles pw , pwis, pwis are given respectively by 2 2 122 22 22 1 22 22 00 1 24 00 0 2 22 44 qwV w Rwsw qwV V D s w w s wsw (41) 2 21 2 00 42 iswy qwV Dwisw i Re swwis (42) and 2 21 3 00 42 iswy qwV Dwisw Re swwis (43) where 222 0 10 Dkck Equations (41), (42) and (43) show the conditions for a large amount of energy to be confined near the surface are 2000wV q (44) 22 20ws (45) and 2 000qwV. (46) Equations (44) and (46) give 2 00qwV (47) which finally gives the d ispersion relation as 0 66 1 tan . w PH PM (48) We will consider only the positive sig n for further dis- cussion. Now Equation (45) gives 22 0 0 2 2 kck s and hence we get the expression for group velocity as 222 2. 2 k Gkks (49) It follows from Equation (49) that 2 G , i.e. the group velocity is less than the shear wav e velocity in the upper mantle. 3. Particular cases Case 1 When 0 th e Equation (48) reduces to 0 66 tan w PH PM (50) which is the dispersion relation for the case when mono- clinic magnetoelastic layer lying over an isotropic half- space. 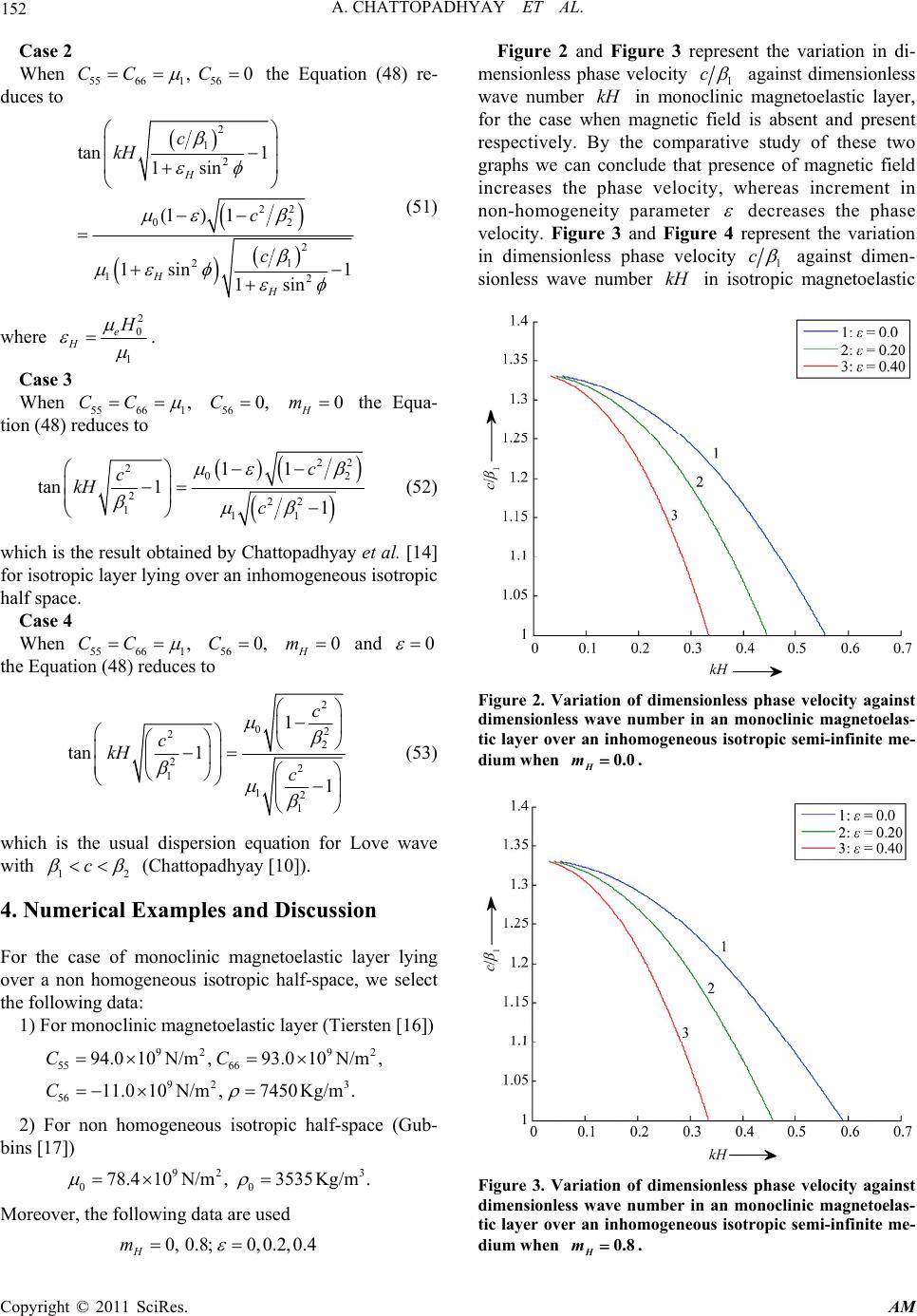 A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 152 Case 2 When 55661 56 ,0CCC the Equation (48) re- duces to 2 1 2 22 02 2 1 2 12 tan 1 1sin (1) 1 1sin1 1sin H HH c kH c c (51) where 2 0 1 e H H . Case 3 When 5566 1,CC 560,C 0 H m the Equa- tion (48) reduces to 22 202 222 111 11 tan 11 c c kH c (52) which is the result obtained by Chatto padhyay et al. [14] for isotropic layer lying over an inhomogeneous isotropic half space. Case 4 When 5566 1,CC 56 0,C 0 H m and 0 the Equation (48) reduces to 2 02 22 22 1 12 1 1 tan 1 1 c c kH c (53) which is the usual dispersion equation for Love wave with 12 c (Chattopadhyay [10]). 4. Numerical Examples and Discussion For the case of monoclinic magnetoelastic layer lying over a non homogeneous isotropic half-space, we select the following data: 1) For monoclinic magnetoelastic layer (Tiersten [16]) 92 92 55 66 92 3 56 94.010 N/m,93.010 N/m, 11.010N/m,7450Kg/m . CC C 2) For non homogeneous isotropic half-space (Gub- bins [17]) 92 3 00 78.410N/m,3535Kg/m . Moreover, the following data are used 0, 0.8;0,0.2,0.4 H m Figure 2 and Figure 3 represent the variation in di- mensionless phase velocity 1 c against dimensionless wave number kH in monoclinic magnetoelastic layer, for the case when magnetic field is absent and present respectively. By the comparative study of these two graphs we can conclude that presence of magnetic field increases the phase velocity, whereas increment in non-homogeneity parameter decreases the phase velocity. Figure 3 and Figure 4 represent the variation in dimensionless phase velocity 1 c against dimen- sionless wave number kH in isotropic magnetoelastic Figure 2. Variation of dimensionless phase velocity against dimensionless wave number in an monoclinic magnetoelas- tic layer over an inhomogeneous isotropic semi-infinite me- dium when 0.0 H m. Figure 3. Variation of dimensionless phase velocity against dimensionless wave number in an monoclinic magnetoelas- tic layer over an inhomogeneous isotropic semi-infinite me- dium when 0.8 H m.  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 153 Figure 4. Variation of dimensionless phase velocity against dimensionless wave number in an isotropic magnetoelastic layer over an inhomogeneous isotropic semi-infinite me- dium when 0.0 H . layer, for the case when magnetic field is absent and present respectively. The presence of magnetic field in- creases the phase velocity, whereas increase in the non- homogeneity parameter decreases the phase velocity. It is observed from Figures 2-4 that presence of mono- clinic medium favours more to the phase velocity as compared to simply isotropic one. The magnetic field and inhomogeneity parameter show similar type of tendency for both the isotropic and monoclinic medium. Figure 6 shows the variation in dimensionless group velocity 2 G with respect to scaled wave number ks. This graph explains that group velocity increases with scaled wave number and approaches to shear wave ve- locity asymptotically. Keeping in the mind the depend- ence of group velocity G on wave number k and depth parameter s, surface plot of group velocity against vary- ing k and s has been drawn in Figure 7. For the case of magnetoelastic isotropic layer lying over a non homogeneous isotropic half-space, we select the following data: 3) For isotropic magnetoelastic layer (Gubbins [17]) 92 3 11 63.410N/m,3364Kg/m . 4) For non homogeneous isotropic half-space (Gub- bins [17]) 92 3 00 78.410N/m,3535Kg/m . Moreover, the following data are used 2 0 1 0,0.8;0,0.2,0.4 e H H Figure 5. Variation of dimensionless phase velocity against dimensionless wave number in an isotropic magnetoelastic layer over an inhomogeneous isotropic semi-infinite me- dium when 0.8 H . Figure 6. Variation of dimensionless group velocity G against scaled wave number ks. 5. Conclusions Dispersion equation for the propagation of G-type seis- mic wave in monoclinic magnetoelastic layer lying over an inhomogeneous isotropic half space is obtained, using the transform technique and Valeev’s method [15]. Con- dition for maximum energy to be confined near the sur- face and expression for group velocity are found. Phase and group velocity curves against wave number are plot- ted taking variation in inhomogeneity parameter. It is ob- served that the presence of non-homogeneity decreases the phase velocity whereas the presence of magnetic field increases the phase velocity, in both the cases when there  A. CHATTOPADHYAY ET AL. Copyright © 2011 SciRes. AM 154 Figure 7. Variation of group velocity G with respect to parameter k and s. is isotropic magnetoelastic layer or monoclinic magneto- elastic layer. It is also observed from the comparative study that presence of monoclinic medium favours more to the phase velocity as compared to simply isotropic one. Group velocity is found lower than the shear wave ve- locity in the upper mantle. The present study has its ap- plication especially to the problem of waves and vibra- tions where the wave signals have to travel through dif- ferent layers of different material properties. This study may be helpful to understand the cause of damages dur- ing large earthquake s; also it may be useful to predict the nature of long period Love waves. These results can also be utilized in the interpretation and analysis of data of geophysical studies. The findings will be useful in fore- casting formation details at greater depth through signal processing and seismic data analysis. The present study may be effectively utilized to generate initial data prior to exploitation of the formation. This stud y may be useful to geophysicist and metallurgist for analysis of rock and material structures through Non-Destructive Testing (NDT). 6. Acknowledgements The authors convey their sincere thanks to Indian School of Mines, Dhanbad for providing JRF to Mr. Abhishek Kr. Singh and also facilitating us with its best facility. Acknowledgement is also due to DST, New Delhi for the providing financial support through Project No. SR/S4/ MS: 436/07, Project title: “Wave propagation in anisot- ropic media”. 7. References [1] B. Gutenberg, “Wave Velocities at Depths between 50 and 600 Kilometers,” Bulletin of the Seismological Soci- ety of America, Vol. 43, 1953, pp. 223-232. [2] B. Gutenberg, “Effects of Low-Velocity Layers,” Pure and Applied Geophysics, Vol. 29, 1954, pp. 1-10. doi:10. 1007/BF01988601 [3] H. Benioff, “Long Waves Observed in the Kamchatka Earthquake of November 4, 1952,” Journal of Geophysi- cal Research, Vol. 63, No. 3, 1958, pp. 589-593. doi:10. 1029/JZ063i003p00589 [4] H. Benioff a nd F. Pre ss, “P rogress Report on Long Period Seismographs,” Geophysical Journal of the Royal Astro- nomical Society, Vol. 1, No. 3, 1958, pp. 208-215. [5] F. Press, “Some Implications on Mantle and Crustal Structure from G-Waves and Love-Waves,” Journal of Geophysical Research, Vol. 64, No. 5, 1959, pp. 565-568. doi:10.1029/JZ064i005p00565 [6] M. Bath and A. L. Arroyo, “Attenuation and Dispersion of G-Waves,” Journal of Geophysical Research, Vol. 67, No. 5, 1962, pp. 1933-1942. doi:10.1029/JZ067i005p01 933 [7] K. Aki, “Generation and Propagation of G-Waves from the Niigata Earthquake of June 16, 1964. Part 2. Estima- tion of Earthquake Moment, Released Energy, and Stress-Strain Drop from the G-Wave Spectrum,” Bulletin of earthquake Research Institute, Tokyo University, Vol. 44, 1966, pp. 73-88. [8] H. Jeffreys, “The Earth,” 4th Edition, Cambridge Univer- sity Press, Cambridge, 1959. [9] J. Bhattacharya, “On Short Period Signals Obtained from Explosions within the Earth,” Pure and Applied Geo- physics, Vol. 55, 1963, pp. 63-71. doi:10.1007/BF0201 1216 [10] A. Chattopadhyay, “On the Generation of G Type Seis- mic Waves,” Acta Geophysical Polonica, Vol. 26, No. 2, 1978, pp. 131-138. [11] N. A. Haskell, “Radiation Pattern of Surface Waves from Point Sources in Multi-Layered Medium,” Bulletin of the Seismological Society of America, Vol. 54, No. 1, 1964, pp. 377-393. [12] A. K. Mal, “On the Generation of G-Waves,” Gerlands Beitrage zur Geophysik, Vol. 72, No. 2, 1962, pp. 82-88. [13] A. Chattopadhyay and A. Keshri, “Generation of G-Type Seismic Waves,” Acta Geophysica Polonica, Vol. 41, No. 1, 1993, pp. 27-35. [14] A. Chattopadhyay, S. Gupta, V. K. Sharma and P. Ku- mari, “Dispersion of G Type Seismic Waves in Low Ve- locity Layer,” International Journal of Applied Engi- neering Research, Vol. 4, No. 3, 2009, pp. 467-479. [15] K. G. Valeev, “On Hill’s Method in the Theory of Linear Differential Equations with Periodic Coefficients,” Jour- nal of Applied Mathematics and Mechanics, Vol. 24, 1960, pp. 1493-1505. doi:10.1016/0021-8928(60)90003-4 [16] H. F. Tiersten, “Linear Piezoelectric Plate Vibrations,” Plenum Press, New York, 1969. [17] D. Gubbins, “Seismology and Plate Tectonics,” Cam- bridge University Press, Cambridge, 1990. |

