World Journal of Mechanics, 2013, 3, 311-318
Published Online November 2013 (http://www.scirp.org/journal/wjm)
http://dx.doi.org/10.4236/wjm.2013.38033
Open Access WJM
Numerical Prediction of Symmetric Water Impact Loads
on Wedge Shaped Hull Form Using CFD
Ahmed Swidan, Walid Amin, Dev Ranmuthugala, Giles Thomas, Irene Penesis
Australian Maritime College, University of Tasmania, Tasmania, Australia
Received September 6, 2013; revised October 5, 2013; accepted October 27, 2013
Copyright © 2013 Ahmed Swidan et al. This is an open access article distributed under the Creative Commons Attribution License,
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
Over the past two decades high-speed vessels have extended their service areas from protected waters to the open ocean
where frequent and large water impacts can result in structural damage. The accurate prediction of slamming loads, and
their consequences on light-weight high-speed vessels, is an essential element of efficient structural design. The aim of
this work is to understand and accurately predict the behavior and local slam loads of quasi-2D wedge shaped hull
forms impacting water. The computed results, using finite-volume Computational Fluid Dynamics (CFD), are validated
against drop test experimental data and compared to a previously published numerical simulation using Smoothed Par-
ticle Hydrodynamics (SPH). The CFD results show good agreement with the experimental measurements.
Keywords: Computational Fluid Dynamics; Slamming; Drop Test
1. Introduction
A major challenge in designing advanced marine vehi-
cles is to achieve efficient structural design. This can
only be accomplished through the accurate prediction of
a vessel’s motion response and the resulting sea loads
[1].
One of the principal sea loads, called slamming, which
is a rapid impulse load due to water impact on, for a
monohull, the vessel’s bottom, or bow flare, and for mul-
tihulls, on the wetdeck between the demihulls [2], see
Figure 1. Slams can cause major global loads as well as
significant local loads on hull panels due to the applied
slam pressures during water entry [3].
A slam may cause severe damage, as reported by Sun
[4], due to significant local loads, and can also excite
the natural modes of the structure, called whipping [5].
This can have a significant influence on reducing the
fatigue life of a vessel as discussed by Thomas et al.
[5,6].
Frequent exposure to slamming can affect the opera-
tional economics by increasing the likelihood of un-
planned docking due to the possibility of fatigue cracks
occurring.
In addition, during ship operations in rough seas, the
master may reduce speed to prevent continuous wave-
induced slamming and excessive accelerations, thereby
limiting the effects of load peaks on the vessel’s structure,
causing a delay in port arrival.
Understanding the behavior of high-speed vessel im-
pacting water, after the vessel becomes partially airborne,
has been for some time considered as the key issue in the
prediction of slam loads.
In collaboration with INCAT Tasmania, the University
of Tasmania (UTAS) has conducted significant research
since 1997 to understand the slamming behavior of
high-speed ships.
This research has involved full scale measurements on
INCAT vessels [8-10], model towing tank experiments
[11,12] and model drop test experiments [1,13].
In full-scale trials, it is difficult to evaluate the slam
Figure 1. Heavy slamming condition at seas [7].

A. SWIDAN ET AL. 312
loads since the researchers do not have control on the
environmental conditions [5,14]. Therefore, drop tests
are usually used to investigate slamming events in a con-
trolled environment [15,16].
Whelan [1] conducted quasi two-dimensional symmet-
rical drop tests of nine scaled models (wedges and cata-
maran hull forms) to capture the essential features of
slam events. The accurate measurement of pressure
around models during water entry was used to propose
design changes to reduce slamming impacts.
Many researchers have developed and/or applied nu-
merical approaches to simulate the behavior of ships
during water entry, including Finite-Volume Method
(FVM) [17], Finite-Element Method (FEM) [18], Finite-
Difference Method (FDM) [19], Smoothed Particle Hy-
drodynamics (SPH) by 2D [20], Boundary Element
Method (BEM) [21] and Fluid Structure Interaction (FSI)
[22].
Validation of these methods has usually been carried
out through benchmark model tests results [23].
This present work is devoted to the prediction wedge-
shaped hull forms behavior during slam events including
motions and local slam loads using quasi 2D finite-
volume CFD. The computed results were validated
against drop test data from a series of experiments con-
ducted by Whelan [1]. The work is also compared to a
set of Smoothed Particle Hydrodynamics’ (SPH) predic-
tions by Shahraki et al. [24] for the same test conditions.
2. Numerical Methods
Advances in computational power have been an essential
element in establishing CFD as a powerful simulation-
based design tool for model and full scale optimizations
in the field of ship hydrodynamics.
CFD is proposed as being capable of solving the slam
problem for complex hull geometry. In such cases, pre-
dicting the ship behaviour using analytical solutions are
generally assessed as being impossible [25].
CFD is faster and cheaper for calculating the detailed
flow-field, hydrodynamic characteristics of new ship
designs in the preliminary design stage than measuring
the same characteristics using scaled model tests. How-
ever, high quality experimental data is needed to validate
the computed results [26].
According to ITTC 2011 [27], CFD could achieve
wider use if; the accuracy of results, grid generation,
turnaround time and complexity of CFD can be im-
proved.
2.1. Numerical Simulation of Free Falling Wedge
Entry
The present work is devoted to the numerical simulation
of a quasi 2D 25˚ deadrise wedge dropped from above
the water surface with a given initial velocity equivalent
to the experimental data, see Table 1 and Figure 2.
The numerical simulations were conducted using the
CFD software STAR-CCM+ Version 7.06.
To assist the validation of the CFD results and to en-
able comparisons with the experimental data the entire
domain was given the dimensions of the UTAS drop test
tank. Length 2.4 m, width 0.3 m and water depth 1 m, as
shown in Figure 2. However, the symmetry of the ge-
ometry about y-z plane and symmetric water entry condi-
tion enabled the domain to be reduced in half. The do-
main thickness was simulated by 25 mm, one cell in the
“y” direction in most of the domain, to reduce the calcu-
lation time, as shown in Figure 3.
Plan view for pressure
Transducers locations
Ø3.8mm
x
z y
P
1
P
4
1DOF Motion
Figure 2. Schematic drop test diagram.
Figure 3. Computational domain.
Open Access WJM

A. SWIDAN ET AL. 313
Table 1. Principal particulars of model section [1].
Type Mass (Kg)
Experimental drop
height (m) Impact velocity (m/s)
Wedge 0.9 0.081 1.22
A multiphase segregated fluid model is employed to
solve the conservation equations for mass, momentum,
and energy for each phase. This model solves the flow
equations for the velocity components and pressure in an
un-coupled manner.
Star-CCM+ uses a Semi-Implicit Method for Pres-
sure-Linked Equations (SIMPLE) algorithm to resolve
the pressure-velocity coupling, while the linkage between
the momentum and continuity equations is achieved
through predictor and corrector stages.
The laminar flow is considered sufficient to capture
the local slamming loads, as the high pressure strikes are
localized in time and space, [28,29].
The free surface was modelled using the Volume of
Fluid (VOF) method based on fluid volume fraction for
solving the equations in both air and water and capturing
the interface between them. The free surface was consid-
ered to be the region between cells comprised entirely of
each of the two fluids, or where the volume fraction of
either fluid is one half and these cells sum to one.
The two fluids mix at their interface and the physical
properties are taken as averages, weighted by the volume
fraction of each of the fluids in these cells. A point on the
water surface defined the free surface position. However,
in order to adequately capture the water flow around the
wedge, it was essential to have a fine grid around the free
surface interface to minimise the smearing effects due to
numerical diffusion.
The drop motion of the wedge was achieved by acti-
vating the vertical motion only in the 6-DOF DFBI (dy-
namic fluid body interaction) rotation and translation
model in STAR-CCM+, which solves the equations of
rigid body motion for all 6-DOF bodies. However in this
case it was reduced to solve it in the vertical direction
only.
The Computational domain consisted of chimera grids,
which are arbitrarily assembled blocks that overlap cov-
ering the following regions, see Figures 3 and 4.
Background region containing the far-field flow do-
main and covered by stationary grid components.
Overset region, extend to some distance from the mov-
ing wedge. The overset mesh is attached to the moving
wedge and covered the overset.
Figure 3 illustrates the interface between the overset
mesh and the background mesh. This region contains
four main types of cells namely active cells, interpolation
(acceptor/donor) cells and inactive (passive) cells. The
overset mesh follows the time history of the body mo-
tions and is influenced by the gravity and fluid resistance;
details can be found in [30].
The mesh was constructed using STAR-CCM+ CFD
software, the calculations were carried out on two hexa-
hedral meshes, see Figure 4.
First, the overset mesh which was refined around each
pressure transducer to capture the rapid slamming pres-
sure instead of refining the whole bottom of the wedge.
Figure 5 shows the effect of grid size on the trans-
ducer geometry. The cell size of 0.3 × 0.3 × 0.3 mm at
the pressure transducers was considered sufficient, see
Figure 5(b); using a coarser mesh would distort the
transducer geometry, see Figure 5(a), and consequently,
will affect the surface average pressure.
The background mesh was refined at the overlapping
region by using assembled blocks, called volumetric
mesh controls. For accuracy, the cell size in the overlap-
ping region, see Figure 5, was similar on all grids that
overlap since if cells sizes are different the accuracy of
interpolation on the coarser grid will determine the accu-
racy of grid coupling.
Linear interpolation was used among each moving ac-
ceptor cell centroid and four donor cells’ centroids for
3D cases.
The fluxes through the cell face between the last active
cell and the acceptor cells were approximated in the same
way as between two active cells. While parts of the
Figure 4. The scalar fields for the background and overset
regions.
(a) (b)
Figure 5. Half of the transducer geometry. (a) Shows a
course grid with 1.2 mm; (b) Shows a fine grid with 0.3 mm.
Open Access WJM

A. SWIDAN ET AL. 314
background grid lying on the moving wedge were deac-
tivated, see Figures 4 and 6.
The simulations were run in series mode on a PC with
Intel CoreTM i7-2600 CPU@3.4 GHz and 16.0 GB RAM.
A sensitivity study was carried out to analyse the ef-
fect of varying the mesh density with suitable time steps
(Courant number varying from 0.05 - 0.5). To ensure
stability, the maximum time step was chosen to satisfy
the Nyquist sampling criterion that requires at least two
time-steps per cell. The minimum time step was chosen
for courant number of 0.1 to capture the pressure peaks.
The CFD uncertainty was approximated by increasing
the mesh density systematically from around 58-388 k
cells.
The total number of cells and cell dimensions are
shown in Table 2, while Figure 7 shows the variations in
Overset Grid
Free Surface
Overlapping
Region
Background
Grid
Figure 6. Symmetry view of the free falling wedge’s grids.
-2
0
2
4
6
8
re (k.Pa)
10
12
14
0 4
Pressu
P me
26
hysical Ti
8
(ms)
1012
Experiment
Grid.No.1
Grid.No.2
Grid.No.3
Grid.No.4
Figure 7. The of the grp
calct prra
Tablent grids used iid size analy-
s
effect
ulated pressure a
id siz
essure t
e and time
nsducer
ste
number
s on the
1.
2. The four differe
is.
n the gr
Grid1Grid 2 Grid 3 Grid 4
Cells 58836 129347 388041388041
Δx 0.01250.00625 0.0031 0.0031
Δy 0.025 0.0125 0.0125 0.0125
Δz 0.01250.00625 0.0031 0.0125
0.00050.0001 0.000050.000025
Time steps (Δsec)
Wall clock time (≈hours) 0.2 0.7 2.3 3.8
Random access memory 4 Gb
the calculated pressures at pressure transducer number 1.
Fr
2.2. SPH Method
using CFD were compared against a
ng among particles were 15 m/s, 5
m
havior of nine two-dimensional 1/40-scale
odels entering still water under drop tests, see Figure 8,
at different conditions for varied wedge and catamaran
geometries. Peak acceleration, velocity time record, av-
erage surface pressure and flow visualization were re-
corded and analysed.
Various models were dropped vertically into still water
using a drop test facility. The facility consisted of a 2.4 m
× 0.3 m × 1.2 m tank with a tower, main post, padded
shock-absorbers and two sets of adjustable bearings, (see,
Figure 8).
om the grid independence study, it was found that us-
ing smaller grid sizes results in predicting higher pres-
sures. Grid 3 was chosen to save the computational time,
as there was only a very slight difference in resulting
pressures between this grid and grid 4.
The obtained results
simulation carried out by [24], using the Smoothed Parti-
cle Hydrodynamics [SPH] technique.
Shahraki et al., studied a range of coefficients of vis-
cosity and speed of sound due to their significant effect
on both computational time and accuracy of results. The
study found that the optimal values for speed of sound,
particle size and spaci
m and 10 mm respectively [24].
3. Model Tests
Whelan [1] investigated the influences of geometry on
lamming bes
m
Figure 8. Drop test tank at University of Tasmania.
Open Access WJM

A. SWIDAN ET AL. 315
The bearings allowed for a free vertical translation
sure at four locations (using grid 3)
ar
he location of the pressure sensors and there-
fo
numerical results with high quality experimental
da
.
mputed peak pressures due to
ch
shows the pressure distribution, around
pr
These times are equivalent to the suggested positions
of preative
pressure zone were found at the wedge chine (se
10) vena contracta.
ng sua
smsteps (courant number around 0.1) are re-
q e
ficient for predicting the impact pressures at P1, P2, P3
and P4.
Figure 12 presents the time history of P1 and its com-
puted value at two different time steps.
Table 3. Main characteristics of the sensors [1].
Sensor Model Range Sensitivity
Resonant
Frequency
motion without vibration.
The gap at each end between the model and the wall of
the tank in the “y” direction set at 5mm based on the re-
sults of a sensitivity study [1].
The data was recorded at a rate of 7042 Hz. In addition
a high-speed camera was used to capture video images of
the flow.
Table 3 shows the relevant specifications of the sen-
sors used.
4. Results and Discussions
The results for wedge’s translation, velocity, vertical
acceleration and pres
e discussed both quantitatively and qualitatively.
It was found that the computed pressures are very sus-
ceptible to t
re a sensitivity study for the location of the pressure
sensors was carried out in which a sensor’s centre loca-
tion was varied to ±1.9 mm of the given location during
experiments. This emphasised the importance of validat-
ing the
ta, as if there is a slight deviation in the position of the
transducer, the error could be duplicated, as shown in
Figures 9 and 10
This study was carried out on P3 transducer, which has
a diameter of 3.8 mm and was located at 0.159 m, 0.05 m,
−0.112 m.
The difference in the co
anging the location in two directions (see Figure 11)
was found to be approximately constant for P3.1 and
result in a 10% reduction for P3.2 (see Figures 9 and
10).
Figure 10
essure transducer number 3, on the wedge hull at three
selected times.
ssure transducer number three. However, neg
e Figure
due to
Due to the rapid chae in presre during wter entry
all time
uired. Therfore, Δs equal 5.0E−5 s was considered suf-
Accelerometer 7290A-30 +/−30 g 66+/−4 mV/g1.5 KHz
Pressure
Transducer 8510B-500 447+/− 0-3 KPa 4.1 KPa/mV 500 KHz
Figure 9. The effect of the location of pressure tranducers
on the computed pressure.
s
Figure 10. Distribution of pressure contours on the wedge
shaped hull form at three different time steps.
Figure 11. Positions of pressure transducer number 3.
Open Access WJM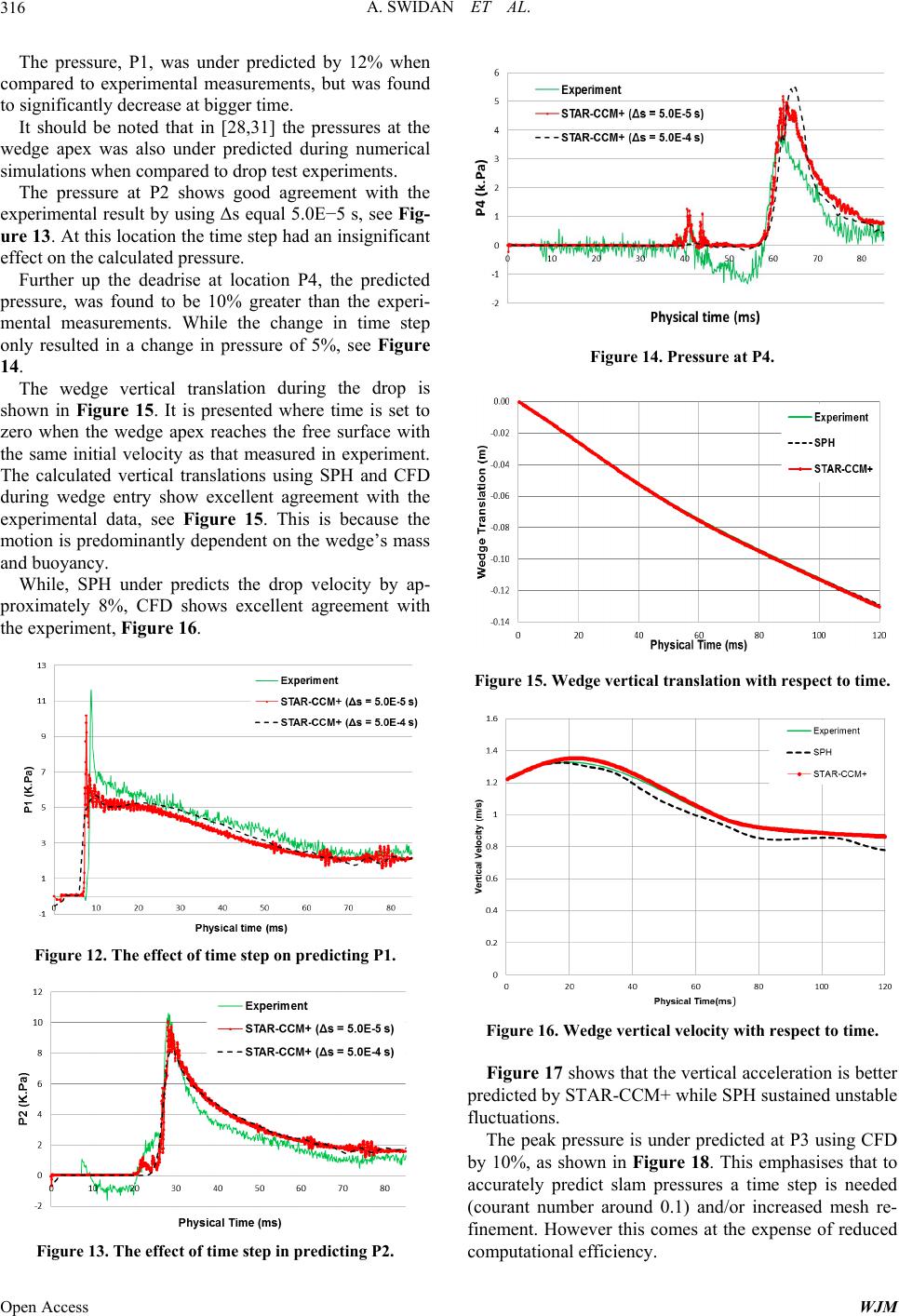

A. SWIDAN ET AL. 316
The pressure, P1, was under predicted by 12% when
compared to experimental measurements, but was found
to significantly decrease at bigger time.
It should be noted that in [28,31] the pressures at the
w
ments. While the change in time step
on
slation during the drop is
own in Figure 15. It is presented where time is set to
zero when the wedge apex reaches the free surface with
the same initial velocity as that measured in experiment.
The calculated vertical translations using SPH and CFD
during wedge entry show excellent agreement with the
experimental data, see Figure 15. This is because the
motion is predominantly dependent on the wedge’s mass
and buoyancy.
While, SPH under predicts the drop velocity by ap-
proximately 8%, CFD shows excellent agreement with
the experiment, Figure 16.
edge apex was also under predicted during numerical
simulations when compared to drop test experiments.
The pressure at P2 shows good agreement with the
experimental result by using Δs equal 5.0E−5 s, see Fig-
ure 13. At this location the time step had an insignificant
effect on the calculated pressure.
Further up the deadrise at location P4, the predicted
pressure, was found to be 10% greater than the experi-
mental measure
ly resulted in a change in pressure of 5%, see Figure
14.
The wedge vertical tran
sh
Figure 12. The effect of time step on predicting P1.
Figure 14. Pressure at P4.
Figure 15. Wedge vertical translation with respect to time.
Figure 16. Wedge vertical velocity with respect to time.
Figure 17 shows that the vertical acceleration is better
predicted by STAR-CCM+ while SPH sustained unstable
fluctuations.
The peak pressure is under predicted at P3 using CFD
by 10%, as shown in Figure 18. This emphasises that to
accurately predict slam pressures a time step is needed
(courant number around 0.1) and/or increased mesh re-
finement. However this comes at the expense of reduced
computational efficiency.
Figure 13. The effect of time step in predicting P2.
Open Access WJM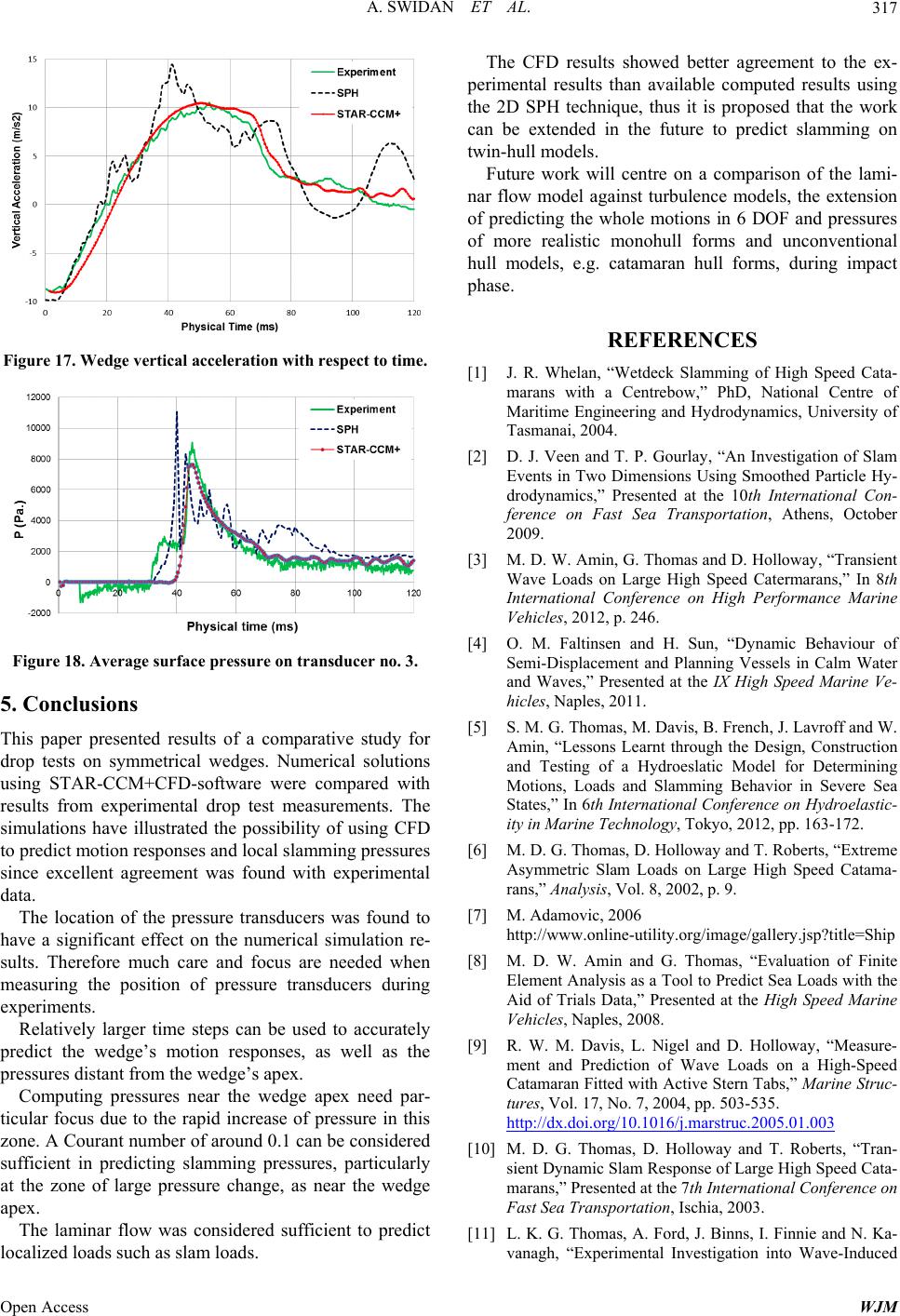

A. SWIDAN ET AL. 317
Figure 17. Wedge vertical acceleration with respect to time.
Figure 18. Average surface pressure on transducer no. 3.
5. Conclusions
This paper presented results of a comparative study for
drop tests on symmetrical wedges. Numerical solutions
using STAR-CCM+CFD-software were compared with
results from experimental drop test measurements. The
simulations have illustrated the possibility of using CFD
to predict motion responses and local slamming pressures
since excellent agreement was found with experimental
data.
The location of the pressure transducers was found to
have a significant effect on the numerical simulation re-
sults. Therefore much care and focus are needed when
measuring the position of pressure transducers during
experiments.
Relatively larger time steps can be used to accurately
predict the wedge’s motion responses, as well as the
pressures distant from the wedge’s apex.
Computing pressures near the wedge apex need par-
ticular focus due to the rapid increase of pressure in this
zone. A Courant number of around 0.1 can be considered
sufficient in predicting slamming pressures, particularly
at the zone of large pressure change, as near the wedge
apex.
The laminar flow was considered sufficient to predict
localized loads such as slam loads.
The CFD results showed better agreement to the ex-
perimental results than available computed results using
the 2D SPH technique, thus it is proposed that the work
can be extended in the future to predict slamming on
twin-hull models.
Future work will centre on a comparison of the lami-
nar flow model against turbulence models, the extension
of predicting the whole motions in 6 DOF and pressures
of more realistic monohull forms and unconventional
hull models, e.g. catamaran hull forms, during impact
phase.
REFERENCES
[1] J. R. Whelan, “Wetdeck Slamming of High Speed Cata-
marans with a Centrebow,” PhD, National Centre of
Maritime Engineering and Hydrodynamics, University of
Tasmanai, 2004.
[2] D. J. Veen and T. P. Gourlay, “An Investigation of Slam
Events in Two Dimensions Using Smoothed Particle Hy-
drodynamics,” Presented at the 10th International Con-
ference on Fast Sea Transportation, Athens, October
2009.
[3] M. D. W. Amin, G. Thomas and D. Holloway, “Transient
Wave Loads on Large High Speed Catermarans,” In 8th
International Conference on High Performance Marine
Vehicles, 2012, p. 246.
[4] O. M. Faltinsen and H. Sun, “Dynamic Behaviour of
Semi-Displacement and Planning Vessels in Calm Water
and Waves,” Presented at the IX High Speed Marine Ve-
hicles, Naples, 2011.
[5] S. M. G. Thomas, M. Davis, B. French, J. Lavroff and W.
Amin, “Lessons Learnt through the Design, Construction
and Testing of a Hydroeslatic Model for Determining
Motions, Loads and Slamming Behavior in Severe Sea
States,” In 6th International Conference on Hydroelastic-
ity in Marine Technology, Tokyo, 2012, pp. 163-172.
[6] M. D. G. Thomas, D. Holloway and T. Roberts, “Extreme
Asymmetric Slam Loads on Large High Speed Catama-
rans,” Analysis, Vol. 8, 2002, p. 9.
[7] M. Adamovic, 2006
http://www.online-utility.org/image/gallery.jsp?title=Ship
[8] M. D. W. Amin and G. Thomas, “Evaluation of Finite
Element Analysis as a Tool to Predict Sea Loads with the
Aid of Trials Data,” Presented at the High Speed Marine
Vehicles, Naples, 2008.
[9] R. W. M. Davis, L. Nigel and D. Holloway, “Measure-
ment and Prediction of Wave Loads on a High-Speed
Catamaran Fitted with Active Stern Tabs,” Marine Struc-
tures, Vol. 17, No. 7, 2004, pp. 503-535.
http://dx.doi.org/10.1016/j.marstruc.2005.01.003
[10] M. D. G. Thomas, D. Holloway and T. Roberts, “Tran-
sient Dynamic Slam Response of Large High Speed Cata-
marans,” Presented at the 7th International Conference on
Fast Sea Transportation, Ischia, 2003.
[11] L. K. G. Thomas, A. Ford, J. Binns, I. Finnie and N. Ka-
vanagh, “Experimental Investigation into Wave-Induced
Open Access WJM

A. SWIDAN ET AL.
Open Access WJM
318
Design Loads on a Large Moored Catamaran,” Ships and
Offshore Structures, Vol. 6, No. 4, 2011, pp. 273-295.
http://dx.doi.org/10.1080/17445301003780581
[12] M. D. J. Lavroff, D. Holloway and G. Thomas, “Wave
Slamming Loads on Wave-Piercer Catamarans Operating
at High-Speed Determined by Hydro-Elastic Segmented
Model Experiments,” Marine Structures, Vol. 33, 2013,
pp. 120-142.
http://dx.doi.org/10.1016/j.marstruc.2013.05.001
[13] M. R. Davis, J. R. Whelan and G. A. Thomas, “Computa-
tional Modeling of Wet Deck Slam Loads with Reference
to Sea Trials,” Presented at the 9th International Confer-
ence on Fast Sea Transportation, Shanghai, 2007.
[14] M. D. G. Thomas, D. Holloway, N. Watson and T. Rob-
erts, “Slamming Response of a Large High-Speed Wave-
Piercer Catamaran,” Marine Technology, Vol. 40, 2003,
pp. 126-140.
[15] A. B. R. Algarín and O. Tascón, “CFD Modeling of 2D
Asymmetric Entry Impact Along with Horizontal Veloc-
ity,” Ship Science & Technology, Vol. 5, 2011, pp.
99-106.
[16] D. W. R. Peterson and C. Frank, “Drop Tests to Support
Water-Impact and Planning Boat Dynamics Theory,”
Dahlgren Division, Naval Surface Warfare Center, Pa-
nama City, Technical Report, 1997.
[17] S. E. H. Mørch, M. Perić and E. Schreck, “Simulation of
Lifeboat Launching under Storm Conditions,” Presented
at the 6th International Conference on CFD in Oil and
Gas, Metallurgical and Process Industries, Trondheim,
2008.
[18] H. W. H. Luo and C. Soares, “Numerical and Experi-
mental Study of Hydrodynamic Impact and Elastic Re-
sponse of One Free-Drop Wedge with Stiffened Panels,”
Ocean Engineering, Vol. 40, 2012, pp. 1-14.
http://dx.doi.org/10.1016/j.oceaneng.2011.11.004
[19] Q. Yang and W. Qiu, “Numerical Simulation of Water
Impact for 2D and 3D Bodies,” Ocean Engineering, Vol.
43, 2012, pp. 82-89.
http://dx.doi.org/10.1016/j.oceaneng.2012.01.008
[20] D. J. Veen and T. P. Gourlay, “A Combined Strip Theory
and Smoothed Particle Hydrodynamics Approach for Es-
timating Slamming Loads on a Ship in Headseas,” Ocean
Engineering, 2012, p. 8.
[21] H. Sun and O. M. Faltinsen, “Numerical Study of Plan-
ning Vessels in Waves,” Journal of Hydrodynamics, Vol.
22, No. 5, 2010, pp. 468-475.
http://dx.doi.org/10.1016/S1001-6058(09)60238-9
[22] M. C. K. Paik, D. Lee and K. Maki, “Strongly Coupled
Fluid-Structure Interaction Method for Structural Loads
on Surface Ships,” Ocean Engineering, Vol. 36, No. 17-
18, 2009, pp. 1346-1357.
http://dx.doi.org/10.1016/j.oceaneng.2009.08.018
[23] DNV, “Environmental Conditions and Environmental
Loads,” Høvik, Norway, Technical Report, 2007.
[24] I. P. J. Shahraki, G. Thomas, M. R. Davis and J. Whelan,
“Prediction of Slamming Behaviour of Monohull and
Multihull Forms Using Smoothed Particle Hydrodynam-
ics,” Presented at the IX HSMV, High Speed Marine Ve-
hicles, Naples, 2011.
[25] V. Bertram, “Practical Ship Hydrodynamics,” UK, 2000.
[26] J. Gorski, “Present State of Numerical Ship Hydrody-
namics and Validation Experiments,” Transactions—
American Society of Mechanical Engineers Journal of
Offshore Mechanics and Arctic Engineering, Vol. 124,
2002, pp. 74-80.
[27] Specialist Committee on CFD in Marine Hydrodynamics,
“Practical Guidelines for Ship CFD Application,” Pre-
sented at the 26th International Towing Tank Conference,
2011.
[28] S. Johannessen, “Use of CFD to Study Hydrodynamic
Loads on Free-Fall Lifeboats in the Impact Phase: A Ve-
rification and Validation Study,” M.Sc. Thesis, Norwe-
gian University of Science and Technology, 2012.
[29] O. M. Faltinsen, “Hydrodynamics of High-Speed Marine
Vehicles,” Cambridge University, USA, 2005.
[30] H. Hidajet, “Development and Application of a Finite
Volume Method for the Computation of Flows around
Moving Bodies on Unstructured, Overlapping Grids,”
PhD, Technische Universitat Hamburg, Harburg, 2005.
[31] A. P. B. Godderidge, S. Lewis, S. Turnock, D. Hudson
and M. Tan, “The Simulation of Free Surface Flows with
Computational Fluid Dynamics,” Presented at the Inspir-
ing Engineering, UK, 2008.