American Journal of Plant Sciences, 2013, 4, 2060-2069
Published Online November 2013 (http://www.scirp.org/journal/ajps)
http://dx.doi.org/10.4236/ajps.2013.411258
Open Access AJPS
Stability of Soybean Genotypes and Their Classification
into Relative Maturity Groups in Brazil
José Elzevir Cavassim1*, João Carlos Bespalhok Filho1, Luis Fernando Alliprandini1,
Ricardo Augusto de Oliveira1, Edelclaiton Daros1, Edson Perez Guerra2
1Department of Plant Science and Crop Protection, Federal University of Parana, Curitiba, Brazil; 2State University of Center-West
(Unicentro), Guarapuava, Brazil.
Received September 5th, 2013; revised October 5th, 2013; accepted October 21st, 2013
Copyright © 2013 José Elzevir Cavassim et al. This is an open access article distributed under the Creative Commons Attribution
License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The stability of soybean genotypes is very important in breeding programs for not only the evaluation, selection, and
production of cultivars but also the establishment of parameters required for the classification of genotypes into relative
maturity groups (RMG). The aim of this study was to define stable genotypes for traits, such as days to flowering, days
to maturity, and length of the reproductive period, and to classify them into RMG. For this purpose, 20 commercial
soybean cultivars were evaluated in 12 environments distributed in the major producing regions of Brazil. Assessments
according to the Eberhart and Russell method and the additive main effects and multiplicative interaction (AMMI)
method were effective in the identification of stable genotypes and their classification into RMG. These methods can
also be used collectively for this purpose. Our results showed that the AMMI method led to a better interpretation of
genotype-environment interactions. Thus, RMG obtained on the basis of stable genotypes represented a good estimate
of the relative maturity of soybean crops throughout Brazil.
Keywords: Glycine max. (L.) Merrill; Genotype-Environment Interaction; Eberhart and Russell Method; AMMI
1. Introduction
The classical approach to describe the maturity of soy-
beans is given by the classification of genotypes into
early, medium, and late phases. In Brazil, breeding com-
panies used a simple categorization based on the matura-
tion cycle of soybean cultivars and classified them as
early, medium early, medium, medium late, and late [1].
This method is effective for evaluating crop maturity
levels in a local setting, but it is not adequate for de-
scribing the relative maturity of soybean crops for a wide
range of environments and latitudes in Brazilian areas
where these crops are being currently cultivated [2]. This
is a simple and effective system from a local standpoint,
but as cultivars are cultivated in different regions and
environments, the results obtained using this old classi-
fication system in such situations may be inaccurate.
Moreover, this system does not consider the effects of
the time of planting.
In the United States, a rating system has been devel-
oped, ranging from Group 00, in the northern region of
the country, to Group VIII, in the southern region of the
country [3]. The adaptation range of each American ma-
turity group is between 200 and 300 km, following a
north-south axis in the territory [4].
Alliprandini et al. [2] conducted the first study on
RMG in Brazil. Using a system similar to the one em-
ployed in the United States, they presented results that
allowed the classification of soybean genotypes into
RMG throughout the country. After the approval of the
Cultivar Protection Law in Brazil [5], several private
companies have released soybean cultivars in the market,
especially genetically modified glyphosate-resistant cul-
tivars. At present, these resistant cultivars account for
approximately 88.8% of the total area cultivated with
soybeans in Brazil [6].
The standardization of cultivar witnesses is essential
for the RMG classification of soybean genotypes to be
effective. Moreover, these standards are required for the
registration and protection of soybean cultivars in Brazil
and need to be used jointly by agricultural improvement
*Corresponding author.

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2061
companies [5].
The genotype-environment interaction (GE) is defined
as the change in the relative performance of genotypes
due to environmental differences. In understanding the
effects of the genotype-environment interaction, the
adaptability and stability of genotypes provide a valuable
tool in the study of relative maturity groups (RMG),
since the adaptation of a cultivar is intrinsically corre-
lated with periods of growth, reproduction, and matura-
tion. This correlation depends on the planting season
because these genotypes are highly affected by the pho-
toperiod [7].
There are many proposed methods for stability evalua-
tion, and the best known is the one proposed by Eberhart
and Russell (ER) [8]. This method is based on simple
linear regression analyses. In this method, a genotype is
considered stable when the regression coefficient is equal
to 1 and the variance of regression deviation is equal to 0,
and additionally when this genotype shows a high aver-
age yield. This regression technique has been useful in
many cases. The main advantages of this method are
interpretability, simplicity, and ability to reduce complex
interactions to an ordered set of linear responses. A more
recent application method, which also allows inferences
of this nature, is additive main effects and multiplicative
interaction (AMMI) analysis. This method combines
statistical techniques, such as analysis of variance and
principal component analysis, to adjust the main effects
(genotype and environment) and GE interaction effects,
respectively [9,10]. The AMMI method can help in the
identification of highly productive and largely adapted
genotypes for performing agronomical zoning, thereby
serving to provide regionalized recommendations and to
allow the selection of test sites [11]. According to Zobel
et al. [10], some advantages of this method include a
more detailed analysis of GE interactions; selection of
genotypes, capitalizing on positive interactions with their
environments; more accurate estimates of genotypic re-
sponses; and easy graphical interpretation of results using
biplots (simultaneous graphical representation of geno-
types and environments).
Cucolotto et al. [12] found that the AMMI method was
effective in explaining the environments and the stability
of soybean cultivars. By employing different populations
in the F2 generation, Maia et al. [13] determined high
stability of the soybean cultivars using the AMMI
method. Silva and Duarte [14] used soybean cultures to
determine stability parameters using different methods
and concluded that the results obtained using the ER and
AMMI methods had a low correlation. Therefore, these
methods should be used in conjunction for classification
purposes.
The aim of this study was to identify stable soybean
genotypes using stability methodologies and classify
them into their RGM, thus obtaining relative maturity
values for any soybean line and cultivar developed
through genetic improvement programs in Brazil.
2. Material and Methods
We evaluated 20 soybean cultivars, which had been ge-
netically modified for resistance to glyphosate by soy-
bean genetic improvement companies in Brazil, with
different attributes of maturity, presence or absence of a
long juvenile period, and different growth types (deter-
minate, semi-determinate, and indeterminate) (Table 1).
The experiments were conducted at different locations in
Brazil, ranging from southern to northern Brazil, during
the agricultural years of 2008/2009 and 2009/2010 in
order to evaluate traits such as flowering behavior and
genotype maturity (Table 1).
For the preparation of the experimental areas, previous
desiccation and fertilization were performed. Sowing was
performed using a no-tillage system, preferably in the
first 2 weeks of November in order to reduce the effects
of photoperiodism, and an experimental seeder. Phyto-
sanitary controls were performed in all plots. Each
5.0-m2 plot consisted of four 5.0-m-long rows, with a
spacing of 0.5 meter, and two external lines, which were
considered as external boundaries.
The experimental design was a randomized block with
two replications per experiment. The following evalua-
tions were performed on each plot: number of days until
the stage R2 (NDF) when 50% of the plants in each plot
had at least one open flower and number of days to ma-
turity (NDM) counted from sowing to maturation, con-
sidering the stage R8 with at least 95% of mature pods
[15]. Lastly, the number of days for the reproductive pe-
riod (NDRP) was defined as the difference between NDF
and NDM, i.e., the period from flowering to full maturity.
After data acquisition, we performed a combined analy-
sis of variance by considering the effects of genotypes,
environments, and GE interactions as random parameters
and the effect of the year of test as a fixed parameter.
Stability analyses were performed according to the ER
method [8] using the program GENES [16] and AMMI
analysis [10] using SAS software [17]. After obtaining
the scores for AMMI analysis, AMMI stability values
(ASV) were calculated using the methodology of [18], as
described below:
()( )
2
2
i
SS IPCA1
ASVIPCA1 IPCA2
SS IPCA2

=+


where SS IPCA1 and SS IPCA2 are the sums of squares
of the AMMI analysis for the first and second axes, re-
spectively, and IPCA1 an IPCA2 are the respective PCA
scores. Genotypes considered stable are those with lower
values of ASV.
Open Access AJPS

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2062
Based on the results of stability analyses, genotypes
considered stable were defined and were used as a refer-
ence for determining regression values for the maturity
parameters. Using the fitting equation, RMG of the re-
maining genotypes were established according to the
method of Alliprandini et al. [2]. Subsequently, the rela-
tive maturity of each genotype was compared with that
reported previously [19].
3. Results and Discussion
3.1. Variance Analysis
The experiments were conducted in various environ-
ments, representing the main regions of soybean cultiva-
tion in Brazil (Table 1). According to the pooled analysis,
low coefficients of variation were obtained for the traits
evaluated (2.3% for NDF, 1.1% for NDM, and 3.3% for
NDRP), indicating good precision in establishing and
conducting the experiments, as reported by Carvalho et
al. [20]. The largest variances for all traits were due to
the effects of location (Table 2). The estimates for aver-
age heritability were above 90%. Interaction effects were
observed in all situations, especially in the year-location
interaction, highlighting the major differences between
the sites tested. However, the year of test had no effect
on any of the traits studied, indicating that the evaluated
years produced no significant differences in these traits
of the genotypes tested. It had been reported that the west
and southwest regions in the state of Paraná, taken in
isolation, had less rain in 2008 [21] compared to other
locations and years, thus influencing the genotypes allo-
cated in this region to some extent. This conclusion re-
garding the influence of the environmental conditions on
genotypes was drawn by assessing the flowering and
ripening periods. Significant differences related to the
year–location interaction are due in part to the great
variability of the environments tested, from southern to
northern Brazil, indicating that, as a whole, years and
locations are distinct environmental parameters and
should both be considered for the correct evaluation of
flowering traits.
The effects of different genotypes were also significant
for the traits evaluated, and greater variability was ob-
served for NDM (Table 2). This range of variation had
also been verified by Alliprandini et al. [2], making it
possible to classify genotypes into distinct RMG, ranging
from 5 to 9. The effects of the genotype-location interac-
tion were also significant for all three traits evaluated,
but with lower variability compared to the main effects.
This indicates that although this interaction exists, be-
cause of regionalized latitude and altitude adaptations,
this effect has little influence on the evaluation of geno-
types for the traits evaluated (Table 2). Alliprandini et al.
[2] reported that the GE interaction was weak for all
traits, suggesting that the classification of genotypes into
RMG can be performed effectively when considering
environments representative of the regions where one
wants to produce and commercialize a cultivar. The
smaller interaction values are related to the interaction
effects of the genotype-year interaction, suggesting that
if an array of experiments representative of the cultiva-
tion sites is installed, the number of years for the evalua-
tion of cultivars can be reduced. Another important as-
pect to be noted is the larger magnitude of the GE inter-
action than the genotype-year interaction. According to
Cruz [16], these interactions require a detailed study of
the behavior of cultivars and the environment by plant
breeders through analysis of stability and adaptability. It
is essential to determine the most stable genotypes with
greater predictability because they will be the bench-
marks for the calculation of maturity [2].
3.2. ER Analysis
Flowering (NDF) and maturity (NDM) data for the crops
showed the expected average values when the crops were
cultivated in their areas of adaptation, since the geno-
types showed a predictable response to the environments
tested, as can be seen by the values of β and R2 (Table 3).
The cultivars mostly showed R2 values above 90%, indi-
cating that the regression equation was well adjusted.
However, we observed that cultivars having a long juve-
nile period, because of breeding programs conducted in
the northern Brazil, tend to increase their flowering pe-
riods when grown in the southern region of the country.
Similarly, a cultivar developed in the southern region,
which hasn’t juvenile traits, tends to accelerate their
flowering and maturation cycles when grown in low lati-
tudes [4]. Allied to this is the effect of temperature be-
cause as we move the crop to the north and places of
lower altitudes, the temperature ranges become higher,
particularly after sowing. However, the effects of differ-
ent latitudes on genotypes is not clearly defined, consid-
ering that in northern cultivars, the long juvenile period
favors a higher initial growth before flowering, causing
prolonged cultivar cycles when sown in the southern
region [22].
Regarding the stability of cultivars, deviation from the
regression for NDF demonstrated that only the cultivar
CD219RR showed lower values that were not significant,
thus indicating good stability. As shown in Table 3, de-
viation values were all highly significant for NDM ac-
cording to the ER method. Thus, all genotypes showed
behavioral differences in maturity, and therefore were
not considered stable by the ER method. One alternative
would be to consider the smaller deviation values com-
bined with β values, but this alternative was not consid-
ered.
Open Access AJPS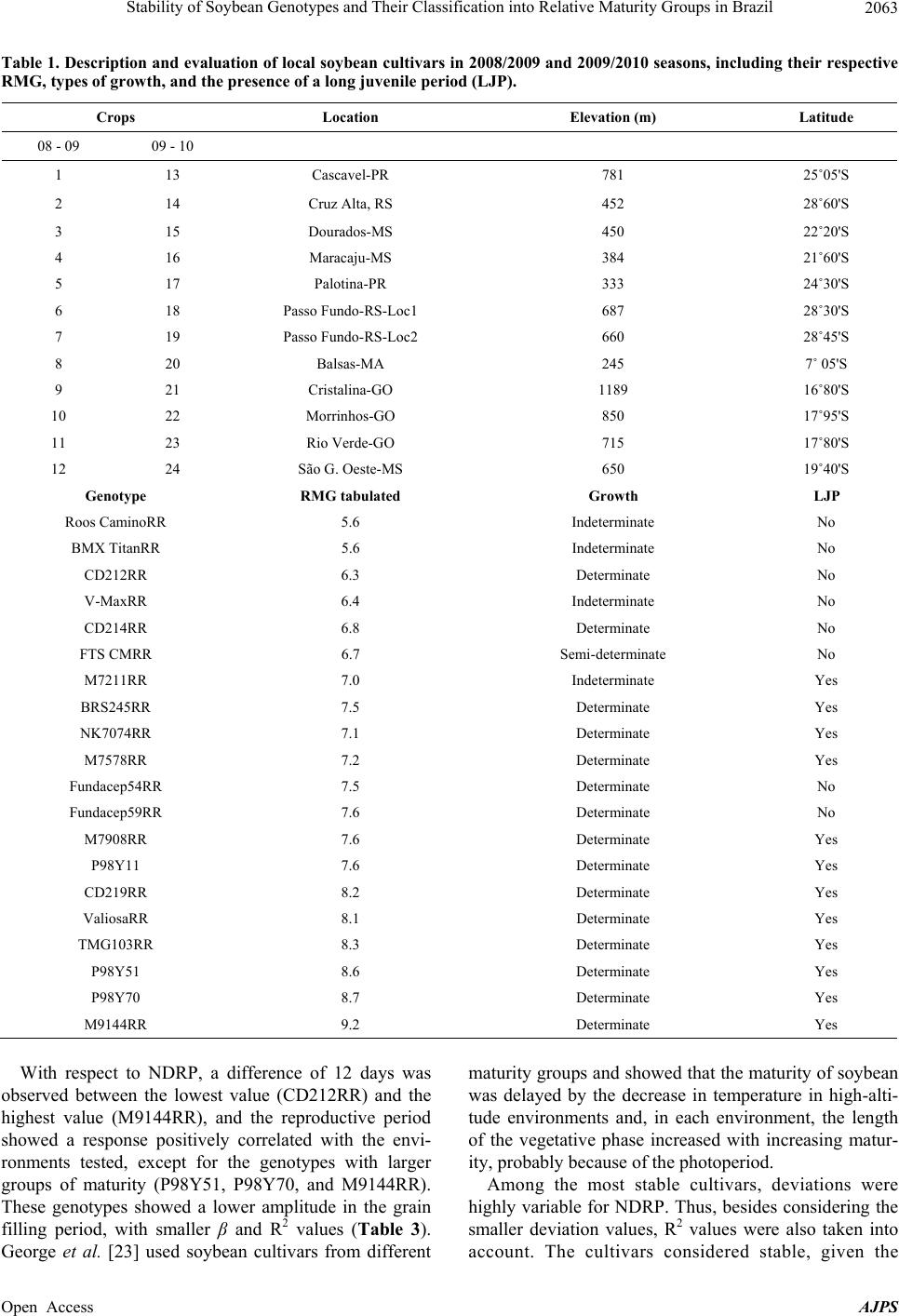

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil
Open Access AJPS
2063
Table 1. Description and evaluation of local soybean cultivars in 2008/2009 and 2009/2010 seasons, including their respective
RMG, types of growth, and the presence of a long juvenile period (LJP).
Crops Location Elevation (m) Latitude
08 - 09 09 - 10
1 13 Cascavel-PR 781 25˚05'S
2 14 Cruz Alta, RS 452 28˚60'S
3 15 Dourados-MS 450 22˚20'S
4 16 Maracaju-MS 384 21˚60'S
5 17 Palotina-PR 333 24˚30'S
6 18 Passo Fundo-RS-Loc1 687 28˚30'S
7 19 Passo Fundo-RS-Loc2 660 28˚45'S
8 20 Balsas-MA 245 7˚ 05'S
9 21 Cristalina-GO 1189 16˚80'S
10 22 Morrinhos-GO 850 17˚95'S
11 23 Rio Verde-GO 715 17˚80'S
12 24 São G. Oeste-MS 650 19˚40'S
Genotype RMG tabulated Growth LJP
Roos CaminoRR 5.6 Indeterminate No
BMX TitanRR 5.6 Indeterminate No
CD212RR 6.3 Determinate No
V-MaxRR 6.4 Indeterminate No
CD214RR 6.8 Determinate No
FTS CMRR 6.7 Semi-determinate No
M7211RR 7.0 Indeterminate Yes
BRS245RR 7.5 Determinate Yes
NK7074RR 7.1 Determinate Yes
M7578RR 7.2 Determinate Yes
Fundacep54RR 7.5 Determinate No
Fundacep59RR 7.6 Determinate No
M7908RR 7.6 Determinate Yes
P98Y11 7.6 Determinate Yes
CD219RR 8.2 Determinate Yes
ValiosaRR 8.1 Determinate Yes
TMG103RR 8.3 Determinate Yes
P98Y51 8.6 Determinate Yes
P98Y70 8.7 Determinate Yes
M9144RR 9.2 Determinate Yes
With respect to NDRP, a difference of 12 days was
observed between the lowest value (CD212RR) and the
highest value (M9144RR), and the reproductive period
showed a response positively correlated with the envi-
ronments tested, except for the genotypes with larger
groups of maturity (P98Y51, P98Y70, and M9144RR).
These genotypes showed a lower amplitude in the grain
filling period, with smaller β and R2 values (Table 3).
George et al. [23] used soybean cultivars from different
maturity groups and showed that the maturity of soybean
was delayed by the decrease in temperature in high-alti-
tude environments and, in each environment, the length
of the vegetative phase increased with increasing matur-
ity, probably because of the photoperiod.
Among the most stable cultivars, deviations were
highly variable for NDRP. Thus, besides considering the
smaller deviation values, R2 values were also taken into
account. The cultivars considered stable, given the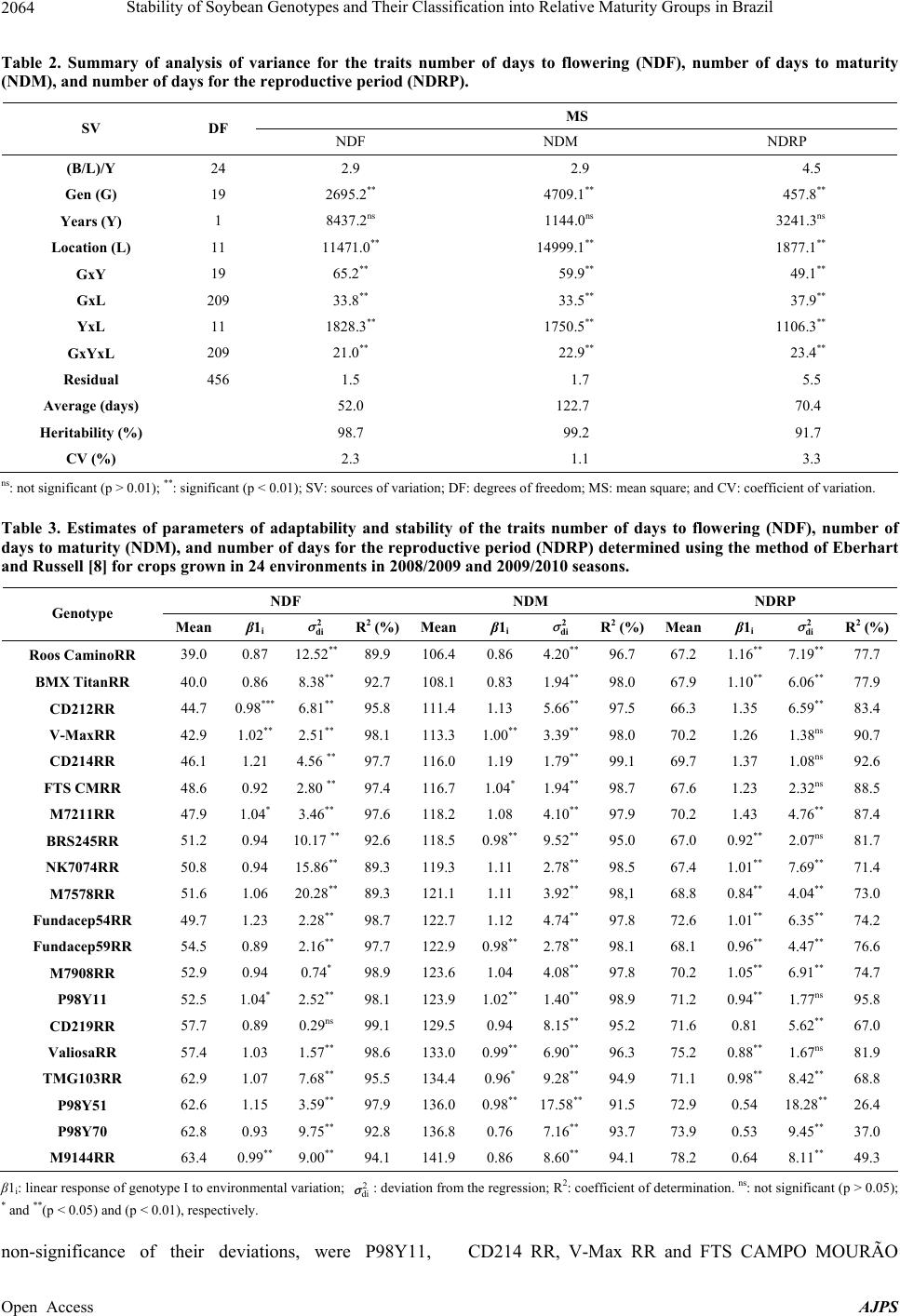

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2064
Table 2. Summary of analysis of variance for the traits number of days to flowering (NDF), number of days to maturity
(NDM), and number of day s for the re pr o ductive period (NDRP).
MS
SV DF NDF NDM NDRP
(B/L)/Y 24 2.9 2.9 4.5
Gen (G) 19 2695.2** 4709.1** 457.8**
Years (Y) 1 8437.2ns 1144.0ns 3241.3ns
Location (L) 11 11471.0** 14999.1** 1877.1**
GxY 19 65.2** 59.9** 49.1**
GxL 209 33.8** 33.5** 37.9**
YxL 11 1828.3** 1750.5** 1106.3**
GxYxL 209 21.0** 22.9** 23.4**
Residual 456 1.5 1.7 5.5
Average (days) 52.0 122.7 70.4
Heritability (%) 98.7 99.2 91.7
CV (%) 2.3 1.1 3.3
ns: not significant (p > 0.01); **: significant (p < 0.01); SV: sources of variation; DF: degrees of freedom; MS: mean square; and CV: coefficient of variation.
Table 3. Estimates of parameters of adaptability and stability of the traits number of days to flowering (NDF), number of
days to maturity (NDM), and number of day s for the reproductive per iod (NDRP) determined using the method of Eberhart
and Russell [8] for crops grown in 24 environments in 2008/2009 and 2009/2010 seasons.
NDF NDM NDRP
Genotype Mean β1i
σ
2
di R2 (%)Meanβ1i
σ
2
di R2 (%)Mean β1i
σ
2
di R2 (%)
Roos CaminoRR 39.0 0.87 12.52** 89.9 106.40.86 4.20** 96.7 67.2 1.16** 7.19** 77.7
BMX TitanRR 40.0 0.86 8.38** 92.7 108.10.83 1.94** 98.0 67.9 1.10** 6.06** 77.9
CD212RR 44.7 0.98*** 6.81** 95.8 111.41.13 5.66** 97.5 66.3 1.35 6.59** 83.4
V-MaxRR 42.9 1.02** 2.51** 98.1 113.31.00** 3.39** 98.0 70.2 1.26 1.38ns 90.7
CD214RR 46.1 1.21 4.56
** 97.7 116.01.19 1.79** 99.1 69.7 1.37 1.08ns 92.6
FTS CMRR 48.6 0.92 2.80
** 97.4 116.7 1.04* 1.94** 98.7 67.6 1.23 2.32ns 88.5
M7211RR 47.9 1.04* 3.46** 97.6 118.21.08 4.10** 97.9 70.2 1.43 4.76** 87.4
BRS245RR 51.2 0.94 10.17
** 92.6 118.50.98** 9.52** 95.0 67.0 0.92** 2.07ns 81.7
NK7074RR 50.8 0.94 15.86** 89.3 119.31.11 2.78** 98.5 67.4 1.01** 7.69** 71.4
M7578RR 51.6 1.06 20.28** 89.3 121.11.11 3.92** 98,1 68.8 0.84** 4.04**73.0
Fundacep54RR 49.7 1.23 2.28** 98.7 122.71.12 4.74** 97.8 72.6 1.01** 6.35** 74.2
Fundacep59RR 54.5 0.89 2.16** 97.7 122.90.98** 2.78** 98.1 68.1 0.96** 4.47**76.6
M7908RR 52.9 0.94 0.74* 98.9 123.61.04 4.08** 97.8 70.2 1.05** 6.91** 74.7
P98Y11 52.5 1.04* 2.52** 98.1 123.91.02** 1.40** 98.9 71.2 0.94** 1.77ns 95.8
CD219RR 57.7 0.89 0.29ns 99.1 129.5 0.94 8.15** 95.2 71.6 0.81 5.62** 67.0
ValiosaRR 57.4 1.03 1.57** 98.6 133.00.99** 6.90** 96.3 75.2 0.88** 1.67ns 81.9
TMG103RR 62.9 1.07 7.68** 95.5 134.40.96* 9.28** 94.9 71.1 0.98** 8.42** 68.8
P98Y51 62.6 1.15 3.59** 97.9 136.00.98** 17.58** 91.5 72.9 0.54 18.28** 26.4
P98Y70 62.8 0.93 9.75** 92.8 136.80.76 7.16** 93.7 73.9 0.53 9.45** 37.0
M9144RR 63.4 0.99** 9.00** 94.1 141.90.86 8.60** 94.1 78.2 0.64 8.11**49.3
β1i: linear response of genotype I to environmental variation; : deviation from the regression; R2: coefficient of determination. ns: not significant (p > 0.05);
* and **(p < 0.05) and (p < 0.01), respectively.
2
di
σ
non-significance of their deviations, were P98Y11, CD214 RR, V-Max RR and FTS CAMPO MOURÃO
Open Access AJPS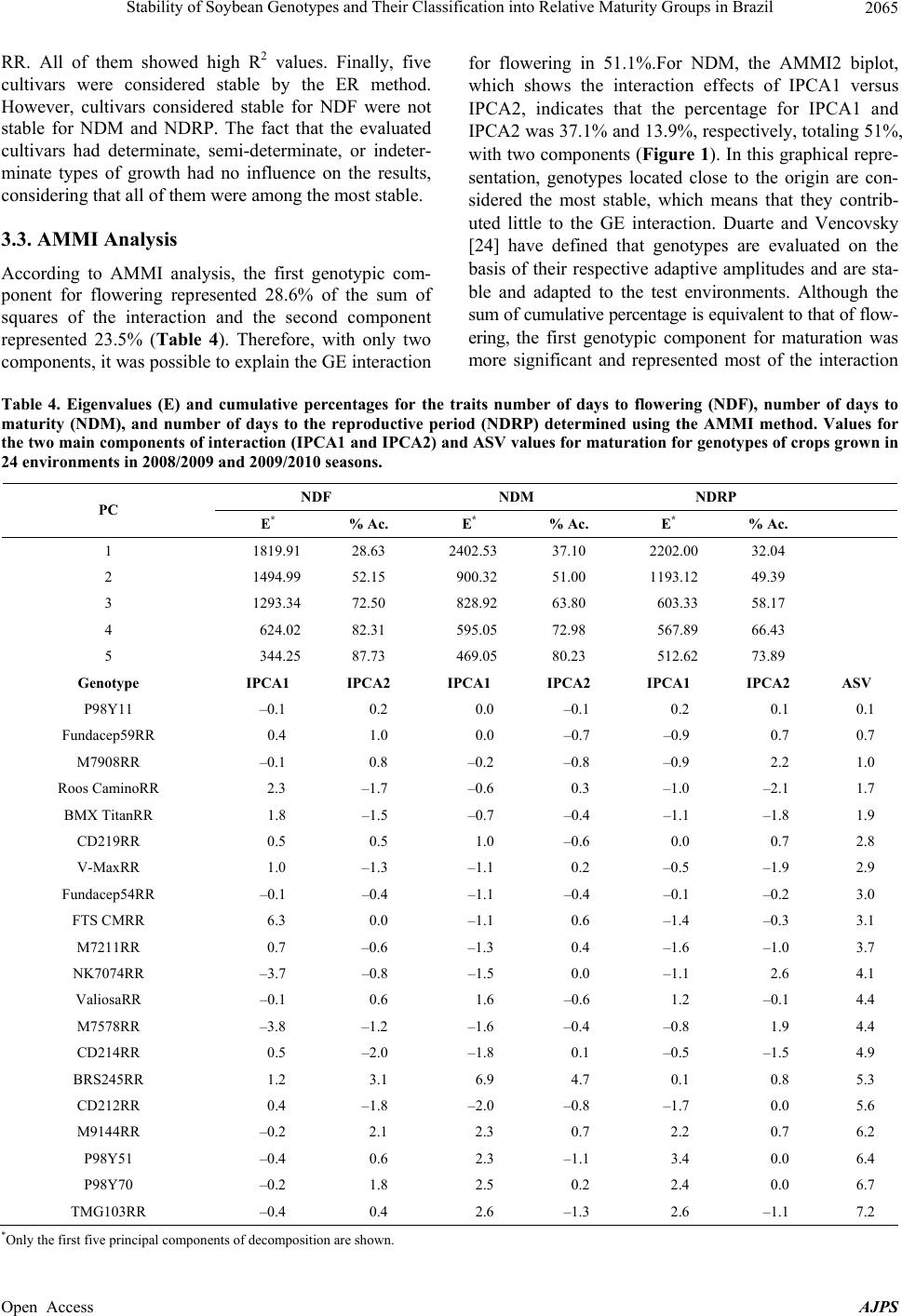

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2065
RR. All of them showed high R2 values. Finally, five
cultivars were considered stable by the ER method.
However, cultivars considered stable for NDF were not
stable for NDM and NDRP. The fact that the evaluated
cultivars had determinate, semi-determinate, or indeter-
minate types of growth had no influence on the results,
considering that all of them were among the most stable.
3.3. AMMI Analysis
According to AMMI analysis, the first genotypic com-
ponent for flowering represented 28.6% of the sum of
squares of the interaction and the second component
represented 23.5% (Table 4). Therefore, with only two
components, it was possible to explain the GE interaction
for flowering in 51.1%.For NDM, the AMMI2 biplot,
which shows the interaction effects of IPCA1 versus
IPCA2, indicates that the percentage for IPCA1 and
IPCA2 was 37.1% and 13.9%, respectively, totaling 51%,
with two components (Figure 1). In this graphical repre-
sentation, genotypes located close to the origin are con-
sidered the most stable, which means that they contrib-
uted little to the GE interaction. Duarte and Vencovsky
[24] have defined that genotypes are evaluated on the
basis of their respective adaptive amplitudes and are sta-
ble and adapted to the test environments. Although the
sum of cumulative percentage is equivalent to that of flow-
ering, the first genotypic component for maturation was
more significant and represented most of the interaction
Table 4. Eigenvalues (E) and cumulative percentages for the traits number of days to flowering (NDF), number of days to
maturity (NDM), and number of days to the reproductive period (NDRP) determined using the AMMI method. Values for
the two main components of interaction (IPCA1 and IPCA2) and ASV values for maturation for genotypes of crops grown in
24 environments in 2008/2009 and 2009/2010 seasons.
NDF NDM NDRP
PC E* % Ac. E* % Ac. E* % Ac.
1 1819.91 28.63 2402.53 37.10 2202.00 32.04
2 1494.99 52.15 900.32 51.00 1193.12 49.39
3 1293.34 72.50 828.92 63.80 603.33 58.17
4 624.02 82.31 595.05 72.98 567.89 66.43
5 344.25 87.73 469.05 80.23 512.62 73.89
Genotype IPCA1 IPCA2 IPCA1 IPCA2 IPCA1 IPCA2 ASV
P98Y11 –0.1 0.2 0.0 –0.1 0.2 0.1 0.1
Fundacep59RR 0.4 1.0 0.0 –0.7 –0.9 0.7 0.7
M7908RR –0.1 0.8 –0.2 –0.8 –0.9 2.2 1.0
Roos CaminoRR 2.3 –1.7 –0.6 0.3 –1.0 –2.1 1.7
BMX TitanRR 1.8 –1.5 –0.7 –0.4 –1.1 –1.8 1.9
CD219RR 0.5 0.5 1.0 –0.6 0.0 0.7 2.8
V-MaxRR 1.0 –1.3 –1.1 0.2 –0.5 –1.9 2.9
Fundacep54RR –0.1 –0.4 –1.1 –0.4 –0.1 –0.2 3.0
FTS CMRR 6.3 0.0 –1.1 0.6 –1.4 –0.3 3.1
M7211RR 0.7 –0.6 –1.3 0.4 –1.6 –1.0 3.7
NK7074RR –3.7 –0.8 –1.5 0.0 –1.1 2.6 4.1
ValiosaRR –0.1 0.6 1.6 –0.6 1.2 –0.1 4.4
M7578RR –3.8 –1.2 –1.6 –0.4 –0.8 1.9 4.4
CD214RR 0.5 –2.0 –1.8 0.1 –0.5 –1.5 4.9
BRS245RR 1.2 3.1 6.9 4.7 0.1 0.8 5.3
CD212RR 0.4 –1.8 –2.0 –0.8 –1.7 0.0 5.6
M9144RR –0.2 2.1 2.3 0.7 2.2 0.7 6.2
P98Y51 –0.4 0.6 2.3 –1.1 3.4 0.0 6.4
P98Y70 –0.2 1.8 2.5 0.2 2.4 0.0 6.7
TMG103RR –0.4 0.4 2.6 –1.3 2.6 –1.1 7.2
*Only the first five principal components of decomposition are shown.
Open Access AJPS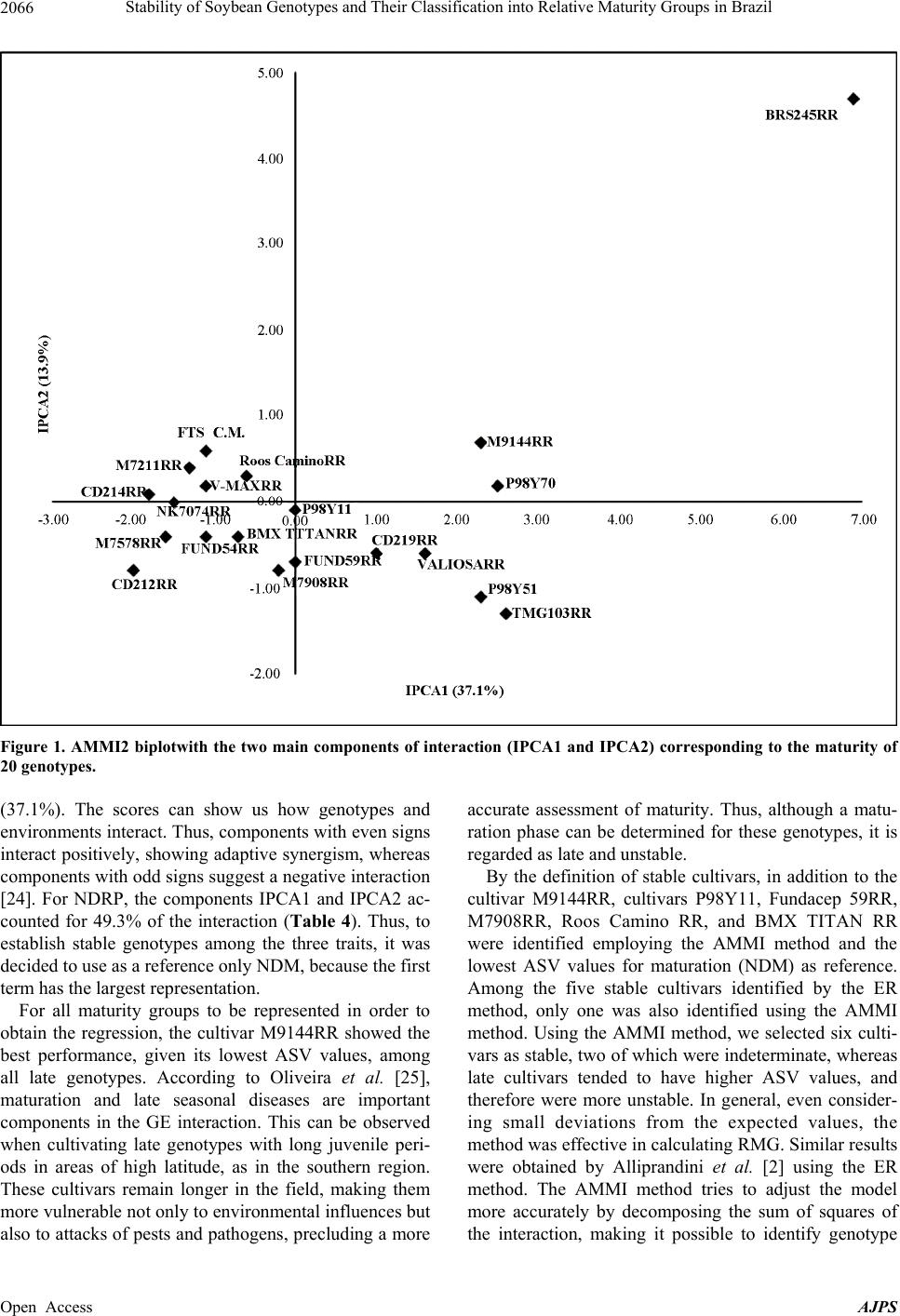

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2066
Figure 1. AMMI2 biplotwith the two main components of interaction (IPCA1 and IPCA2) corresponding to the maturity of
20 genotypes.
(37.1%). The scores can show us how genotypes and
environments interact. Thus, components with even signs
interact positively, showing adaptive synergism, whereas
components with odd signs suggest a negative interaction
[24]. For NDRP, the components IPCA1 and IPCA2 ac-
counted for 49.3% of the interaction (Table 4). Thus, to
establish stable genotypes among the three traits, it was
decided to use as a reference only NDM, because the first
term has the largest representation.
For all maturity groups to be represented in order to
obtain the regression, the cultivar M9144RR showed the
best performance, given its lowest ASV values, among
all late genotypes. According to Oliveira et al. [25],
maturation and late seasonal diseases are important
components in the GE interaction. This can be observed
when cultivating late genotypes with long juvenile peri-
ods in areas of high latitude, as in the southern region.
These cultivars remain longer in the field, making them
more vulnerable not only to environmental influences but
also to attacks of pests and pathogens, precluding a more
accurate assessment of maturity. Thus, although a matu-
ration phase can be determined for these genotypes, it is
regarded as late and unstable.
By the definition of stable cultivars, in addition to the
cultivar M9144RR, cultivars P98Y11, Fundacep 59RR,
M7908RR, Roos Camino RR, and BMX TITAN RR
were identified employing the AMMI method and the
lowest ASV values for maturation (NDM) as reference.
Among the five stable cultivars identified by the ER
method, only one was also identified using the AMMI
method. Using the AMMI method, we selected six culti-
vars as stable, two of which were indeterminate, whereas
late cultivars tended to have higher ASV values, and
therefore were more unstable. In general, even consider-
ing small deviations from the expected values, the
method was effective in calculating RMG. Similar results
were obtained by Alliprandini et al. [2] using the ER
method. The AMMI method tries to adjust the model
more accurately by decomposing the sum of squares of
the interaction, making it possible to identify genotype
Open Access AJPS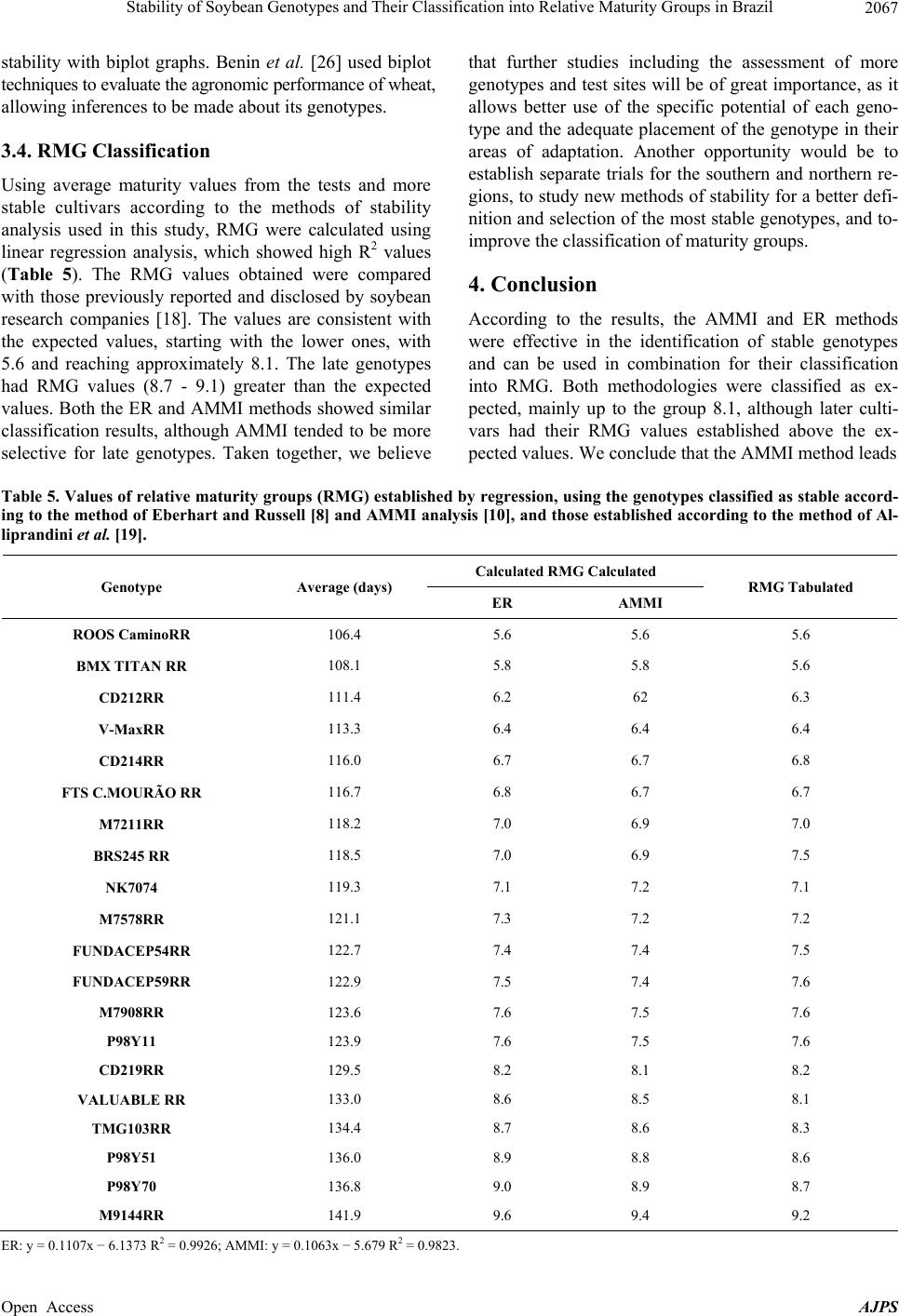

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2067
stability with biplot graphs. Benin et al. [26] used biplot
techniques to evaluate the agronomic performance of wheat,
allowing inferences to be made about its genotypes.
3.4. RMG Classification
Using average maturity values from the tests and more
stable cultivars according to the methods of stability
analysis used in this study, RMG were calculated using
linear regression analysis, which showed high R2 values
(Table 5). The RMG values obtained were compared
with those previously reported and disclosed by soybean
research companies [18]. The values are consistent with
the expected values, starting with the lower ones, with
5.6 and reaching approximately 8.1. The late genotypes
had RMG values (8.7 - 9.1) greater than the expected
values. Both the ER and AMMI methods showed similar
classification results, although AMMI tended to be more
selective for late genotypes. Taken together, we believe
that further studies including the assessment of more
genotypes and test sites will be of great importance, as it
allows better use of the specific potential of each geno-
type and the adequate placement of the genotype in their
areas of adaptation. Another opportunity would be to
establish separate trials for the southern and northern re-
gions, to study new methods of stability for a better defi-
nition and selection of the most stable genotypes, and to-
improve the classification of maturity groups.
4. Conclusion
According to the results, the AMMI and ER methods
were effective in the identification of stable genotypes
and can be used in combination for their classification
into RMG. Both methodologies were classified as ex-
pected, mainly up to the group 8.1, although later culti-
vars had their RMG values established above the ex-
pected values. We conclude that the AMMI method leads
Table 5. Values of relative maturity groups (RMG) established by regression, using the genoty pes classified as stable accord-
ing to the method of Eberhart and Russell [8] and AMMI analysis [10], and those established according to the method of Al-
liprandini et al. [19].
Calculated RMG Calculated
Genotype Average (days)
ER AMMI
RMG Tabulated
ROOS CaminoRR 106.4 5.6 5.6 5.6
BMX TITAN RR 108.1 5.8 5.8 5.6
CD212RR 111.4 6.2 62 6.3
V-MaxRR 113.3 6.4 6.4 6.4
CD214RR 116.0 6.7 6.7 6.8
FTS C .MOURÃO RR 116.7 6.8 6.7 6.7
M7211RR 118.2 7.0 6.9 7.0
BRS245 RR 118.5 7.0 6.9 7.5
NK7074 119.3 7.1 7.2 7.1
M7578RR 121.1 7.3 7.2 7.2
FUNDACEP54RR 122.7 7.4 7.4 7.5
FUNDACEP59RR 122.9 7.5 7.4 7.6
M7908RR 123.6 7.6 7.5 7.6
P98Y11 123.9 7.6 7.5 7.6
CD219RR 129.5 8.2 8.1 8.2
VALUABLE RR 133.0 8.6 8.5 8.1
TMG103RR 134.4 8.7 8.6 8.3
P98Y51 136.0 8.9 8.8 8.6
P98Y70 136.8 9.0 8.9 8.7
M9144RR 141.9 9.6 9.4 9.2
E
R: y = 0.1107x − 6.1373 R2 = 0.9926; AMMI: y = 0.1063x − 5.679 R2 = 0.9823.
Open Access AJPS

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2068
to a better interpretation of the GE interactions. We sug-
gest furthering these studies by employing other method-
ologies and by separating the southern and northern en-
vironments to determine the best fit for RMG.
5. Acknowledgements
We thank the following researchers and institutions for
their valuable contribution to the study: Leonardo
Oliveira and Eduardo Lambert (MONSOY), Marco Rott
(COODETEC), Andreomar Kurek (Syngenta), Cleiton
Steckling (FUNDACEP), Carlos Pitol (FUNDAÇÃO
MS), Nizio Giasson and Marcos Matsumoto (DON
MARIO), Paulo Bertagnolli and Maria do Rosário
Teixeira (EMBRAPA), Anderson Dona (WEHRTEC),
and Luis Stabile (SOYTECH).
REFERENCES
[1] L. F. Alliprandini, J. F. F. Toledo, N. Fonseca Jr., L. A.
Almeida and R. A. S. Kiihl, “Effects of Genotype-
Environment Interaction on Soybean Yield in the Paraná
State,” Pesquisa Agropecuária Brasileira, Vol. 29, No. 9,
1994, pp. 1433-1444.
[2] L. F. Alliprandini, C. Abatti, P. F. Bertagnolli, J. E. Ca-
vassim, H. L. Gabe, A. Kurek, M. N. Matsumoto, M. A.
R. Oliveira, C. Pitol, L. C. Prado and C. Steckling, “Un-
derstanding Soybean Maturity Groups in Brazil: Environ-
ment, Cultivar Classification, and Stability,” Crop Science,
Vol. 49, No. 3, 2009, pp. 801-808.
http://dx.doi.org/10.2135/cropsci2008.07.0390
[3] L. X. Zhang, S. Kyei-Boahen, J. Zhang, M. H. Zhang, T.
B. Freeland, C. E. Watson Jr. and X. M. Liu, “Modifica-
tions of Optimum Adaptation Zones for Soybean Matur-
ity Groups in the USA,” Crop Management. (Online)
http://dx.doi.org/10.1094/CM-2007-0927-01-RS
[4] H. A. Bruns, “A Survey of Factors Involved in Crop Ma-
turity,” Agronomy Journal, Vol. 101, No. 1, 2009, pp. 60-
66. http://dx.doi.org/10.2134/agronj2007.0271R
[5] Brazil, “Ministry of Agriculture, Livestock and Supply.
Cultivar Protection in Brazil,” MAPA/ACS, Brasília,
2011, p. 202.
[6] Céleres, “Biotechnology Report,” Céleres Consulting,
Uberlandia, 2012, p. 9.
[7] G. V. Meotti, G. Benin, R. R. Silva, E. Beche and L. B.
Munaro, “Sowing Dates and Agronomic Performance of
Soybean Cultivars,” Pesquisa Agropecuária Brasileira,
Vol. 47, No. 1, 2012, pp. 14-21.
http://dx.doi.org/10.1590/S0100-204X2012000100003
[8] S. A. Eberhart and W. A. Russell, “Stability Parameters
for Comparing Varieties,” Crop Science, Vol. 6, No. 1,
1966, pp. 36-40.
http://dx.doi.org/10.2135/cropsci1966.0011183X0006000
10011x
[9] R. A. Kempton, “The Use of Biplots in Interpreting Vari-
ety by Environment Interactions,” Journal of Agricultural
Science, Vol. 103, No. 1, 1984, pp. 123-135.
http://dx.doi.org/10.1017/S0021859600043392
[10] R. W. Zobel, M. J. Wright and H. G. Gauch, “Statistical
Analysis of a Yield Trial,” Agronomy Journal, Vol. 80,
No. 3, 1988, pp. 388-393.
http://dx.doi.org/10.2134/agronj1988.0002196200800003
0002x
[11] H. G. Gauch and R. W. Zobel, “AMMI Analysis of Yield
Trials,” In: M. S. Kang and H. G. Gauch, Eds., Genotype-
by-Environment Interaction, CRC Press, New York, 1996,
p. 416.
[12] M. Cucolotto, V. C. Pípolo, D. D. Garbuglio, N. S.
Fonseca Jr., D. Destro and M. K. Kamikoga, “Genotype ×
Environment Interaction in Soybean: Evaluation through
Three Methodologies,” Crop Breeding and Applied Bio-
technology, Vol. 7, No. 3, 2007, pp. 270-277.
[13] M. C. C. Maia, N. A. Vello, M. M. Rocha, J. B. Pinheiro
and N. F. Silva Jr., “Adaptability and Stability of Soybean
Experimental Lines Selected for Agronomic Traits and
Insect Resistance by Uni-Multivariate Method,” Bragantia,
Vol. 65, No. 2, 2006, pp. 215-226.
http://dx.doi.org/10.1590/S0006-87052006000200004
[14] W. C. J. Silva and J. B. Duarte, “Statistical Methods to
Study Phenotypic Adaptability and Stability in Soybean,”
Pesquisa Agropecuária Brasileira, Vol. 41, No. 1, 2006,
pp. 23-30.
http://dx.doi.org/10.1590/S0100-204X2006000100004
[15] W. R. Fehr and C. E. Caviness, “Stages of Soybean De-
velopment,” Special Report 80, Iowa State University,
Ames, 1977.
[16] C. D. Cruz, “Genes Program: Windows Version: Ap-
plication in Genetics and Statistics,” Editora UFV, Viçosa,
2001, p. 648.
[17] SAS Institute, “SAS User’s Guide,” SAS Institute, Cary,
1999.
[18] J. L. Purchase, H. Hatting and C. S. Van Deventer,
“Genotype × Environment Interaction of Winter Wheat in
South Africa: II. Stability Analysis of Yield Perform-
ance,” South African Journal of Plant Soil, Vol. 17, No. 3,
2000, pp. 101-107.
http://dx.doi.org/10.1080/02571862.2000.10634878
[19] L. F. Alliprandini, J. E.Cavassim, M. A. R. Oliveira, M.
N. Matsumoto, L. C. Prado, C. Pitol, C. Steckling, P. F.
Bertagnoli, A. Kurek, M. K. Kamikoga, A. Dona, N. F.
Giasson, C. Abatti, G. D. Silveira and C. Takeda,
“Classification of Soybean Cultivarsin to Relative
Maturity Groups in Brazil, during 2001/2002-2011/2012
Seasons,” 7th Congress of Plant Breeding, SBMP,
Uberlandia, 2013.
[20] C. G. P. Carvalho, C. A. A. Arias, J. F. F. Toledo, L. A.
Almeida, R. A. S. Kiihl and M. F. Oliveira, “Genotypex
Environment Interaction on Soybean Production Perform-
ance in Paraná,” Pesquisa Agropecuária Brasileira, Vol.
37, No. 7, 2002, pp. 989-1000.
http://dx.doi.org/10.1590/S0100-204X2002000700013
[21] Simepar, “Condições do Tempo,” 2013.
http://www.simepar.br/tempo/clima/aviso_verao2009.htm
[22] D. Destro, V. Carpentieri-Pípolo, R. A. S. Kiihl and L. A.
Almeida, “Photoperiodic and Genetic Control of the Long
Open Access AJPS

Stability of Soybean Genotypes and Their Classification into Relative Maturity Groups in Brazil 2069
Juvenile Period in Soybean: A Review,” Crop Breeding
and Applied Biotechnology, Vol. 1, No. 1, 2001, pp. 72-
92. http://dx.doi.org/10.13082/1984-7033.v01n01a10
[23] T. George, D. P. Bartholomew and P. W. Singleton, “Ef-
fect of Temperature and Maturity Group on Phenology of
Field Grown Nodulating and Nonnodulating Soybean
Isolines,” Biotronics, Vol. 19, 1990, pp. 49-59.
[24] J. B. Duarte and R. Vencovsky, “Genotypex Environment
Interaction: An Introduction to AMMI Analysis,” Série
Monograph Series, Brazilian Society of Genetics, Ribeirao
Preto, 1999.
[25] A. B. Oliveira, J. B. Duarte, L. J. Chaves and M. A.
Couto, “Environmental and Genotypic Factors Associated
with Genotype by Environment Interactions in Soybean,”
Crop Breeding and Applied Biotechnology, Vol. 6, 2006,
pp. 79-86.
[26] G. Benin, C. Pinnow, C. L. Silva, E. S. Pagliosa, E.
Beche, E. Bornhofen, L. B. Munaro and R. R. Silva,
“Biplot Analysis in the Evaluation of Wheat Cultivarsat
Different Levels of Management,” Bragantia, Campinas,
Vol. 71, No. 1, 2012, pp. 28-36.
Open Access AJPS