Paper Menu >>
Journal Menu >>
 Journal of Applied Mathematics and Physics, 2013, 1, 128-143 Published Online November 2013 (http://www.scirp.org/journal/jamp) http://dx.doi.org/10.4236/jamp.2013.15019 Open Access JAMP Higher Order Aitken Extrapolation with Application to Convergin g and Div e r g i ng Gauss-Seidel Iterations Ababu Teklemariam Tiruneh Department of Environmental Health Science, University of Swaziland, Mbabane, Swaziland Email: ababute@yahoo.com Received October 13, 2013; revised November 13, 2013; accepted November 20, 2013 Copyright © 2013 Ababu Teklemariam Tiruneh. This is an open access article distributed under the Creative Commons Attribu- tion License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In this paper, Aitken’s extrapolation normally applied to convergent fixed point iteration is extended to extrapolate the solution of a divergent iteration. In addition, higher order Aitken extrapolation is introduced that enables successive decomposition of high Eigen values of the iteration matrix to enable convergence. While extrapolation of a convergent fixed point iteration using a geometric series sum is a known form of Aitken acceleration, it is shown that in this paper, the same formula can be used to estimate the solution of sets of linear equations from diverging Gauss-Seidel iterations. In both convergent and divergent iterations, the ratios of differences among the consecutive values of iteration eventu- ally form a convergent (divergent) series with a factor equal to the largest Eigen value of the iteration matrix. Higher order Aitken extrapolation is shown to eliminate the influence of dominant Eigen values of the iteration matrix in suc- cessive order until the iteration is determined by the lowest possible Eigen values. For the convergent part of the Gauss-Seidel iteration, further acceleration is made possible by coupling of the extrapolation technique with the succes- sive over relaxation (SOR) method. Application examples from both convergent and divergent iterations have been provided. Coupling of the extrapolation with the SOR technique is also illustrated for a steady state two dimensional heat flow problem which was solved using MATLAB programming. Keywords: Linear Equations; Gauss-Seidel Iteration; Aitken Extrapolation; Acceleration Technique; Iteration Matrix; Fixed Point Iteration 1. Introduction Iterative solutions to systems of equations are widely employed for solving scientific problems. They have several advantages over direct methods. For equations involving large number of unknowns iterative solutions involve operations of order (n2) compared to direct solu- tions of order (n3). In computer applications, iterative solutions require much less memory and are quite simple to program [1]. In addition iterative solutions are in many cases applicable to non-linear sets of equations. One set of iterative methods that are in wide use is centered on generation of Krylov sub space such as the method of conjugate gradients developed by Hestens and Stiefel [2]. Such methods are guaranteed to converge in at most N steps for problems involving N unknowns. However, iterative solutions based on stationary methods such as Gauss-Seidel and others that are simpler to pro- gram and do not generate new iteration matrix are re- ceiving greater application [3]. Iterative methods that mimic the physical processes involved such as the for- ward-backward method have been shown to produce solutions for some problems faster than Krylov methods [4]. However, fixed point iterative methods are known to be less robust than Krylov methods and convergence is not guaranteed for ill-conditioned systems of equations. Iterative processes involving fixed point iterations that are convergent such as Jacobi and Gauss-Seidel iterations are known to form error series that are diminishing in the form of geometric series [5,14,16]. The geometric series sum based form of Aitken extrapolation for fixed point iteration involving the system of equations A XB is based on the formula [6]: 1 k k E XX where X is the Aitken extrapolation of the solution, Xk is the approximation to the solution at the kth iteration, Ek is the difference in X at the kth iteration 1– kk XX and  A. T. TIRUNEH 129 is the ratio of the difference in X values 1kk EE . The geometric series extrapolation requires at least three points of the iteration. The extrapolation in terms of the three points at the k, k + 1 and k + 2 iterations takes the form [6]. 21 21 2 kk kk kk XX XX X1 k X XX which is a known form of Aitken extrapolation. Irons and Shrive [7] made a modification to Aitken’s method for scalars (sequences) which can also be applied to individual x values of fixed point iterations such as the Gauss-Seidel iteration. The extrapolation to the fifth point uses four points. After the four point extrapolation the fixed point iteration formula is used to obtain the fifth point. In this way by joint application of both extrapola- tion and fixed point iteration, the method is said to be dynamic with better convergence properties. A dynamic model in such a form does not require restarting the it- eration procedure as the method generates all necessary iterates from the latest extrapolation [8]. The reduced rank extrapolation method [9] extends the scalar form of Aitken extrapolation into vectors of a given dimension. The extrapolation formulation for the iteration vector is a vector parallel of Aitken’s extrapola- tion: 1 K K X XMIE where M is the iteration matrix of the fixed point itera- tion, I is the identity matrix of rank N, X are the iteration vector and Ek is the vector difference in X at the kth itera- tion. The method involves computing the generalized inverse involving the second order difference vector and is time consuming for solving non-linear systems of equations of larger size. Gianola and Schaffer [6] applied geometric series ex- trapolation for Jacobi and Gauss-Seidel iterations in ani- mal models. The optimal relaxation factor was lower when solutions were extrapolated, but its value was not as critical in the case of extrapolation. Fast Eigen vector computations that require matric in- version or decomposition are unsuitable for large size matrix problems as many of them involve operations of the order O(n3). Kamvar, et al. [10] applied Aitken ex- trapolation for accelerating page rank computations. They showed that Aitken acceleration computes the prin- cipal eigenvector of a Markov matrix under the assump- tion that the power-iteration estimate x k can be ex- pressed as a linear combination of the first two eigen- vectors. Calude Breziniski and Michela Redivo Zaglia [11] proposed extension of Aitken’s extrapolation into a gen- eral form involving transforming the sequence of itera- tion into a different form using known sequences which can lead to stabilization and convergence of the original iteration. The transformation, however, is not simple and straight forward and required further refinement. Chebyshev acceleration is also a way of transforming the iteration sequence which, for iteration matrix of known upper and lower bound Eigen values, the trans- formed sequence using Chebyshev polynomials leads to convergence of the fixed point iteration. In Chebyshev acceleration, the sequence of iteration values is modified by multiplication with Chebyshev polynomials which are constructed from known or estimated ranges of Eigen values of the iteration matrix. The choice of the form of Chebyshev polynomials is such that the procedure leads to progressive reduction of the norm of the error vector through a min-max property which minimizes the maxi- mum value that the polynomial has for the range of Ei- gen values specified [12]. However, Chebyshev accelera- tion has the drawback of the need to accurately estimate the bounds of Eigen values of the iteration matrix, be- cause outside the domain of Eigen values the polynomial shows divergence and the min-max property does not hold. The following sections in this paper will give the basis of Aitken extrapolation for convergent fixed point itera- tions and the derivation for the extension of the extrapo- lation to divergent fixed point iterations. The paper con- tinues by introducing higher order Aitken extrapolation and shows how each order of extrapolation successively reduces the rank of Eigen values which helps in stabiliz- ing the extrapolation of a divergent iteration. Thereafter, application examples of both convergent and divergent fixed point iterations follow that include finite difference solution of Laplace equation to a two dimensional heat flow problem which was solved using MATLAB pro- gramming. 2. Method Development For solving a system of linear equations using fixed point iteration, the Aitken extrapolation formula can be written in the form: 1 k kk e xx where: x = The estimate of the solution at the limit of itera- tion; ek = The difference in consecutive x values, i.e., 1kk x x ; k = The ratio of differences in x values, i.e., 12 1 kkk kkkk exx exx 1 It will now be shown that the above formula is appli- cable to both convergent as well as divergent Gauss- Seidel iteration. In addition it will also be shown that successive application of the Aitken extrapolation for- Open Access JAMP  A. T. TIRUNEH Open Access JAMP 130 The differences in the solution vector Xk among con- secutive steps of iteration are formulated as follows: mula to a higher order will result in deflation of the dominant Eigen values one by one there by transforming a divergent iteration to a convergent form. Let the system of linearized equations for a given problem be represented in the matrix form: A XB where A is the coefficient matrix, B is the right hand side vector and X is the solution vector. Writing the matrix A further in terms of the components L, U and D matrices gives A ULD where U and L are the upper and low triangular matrices respectively and D is the diagonal matrix. For the Gauss-Seidel iteration, the system of equations now can be written as: ULDX B L DXUX B Using the (k + 1)th and kth iteration X-vectors for the left and right hand sides of equation above respectively; 1kk L DXUX B Solving for 1k X ; 11 1kk XLDUXLD B (1) This is the Gauss-Seidel iteration and the matrix; 1 LD U is called the iteration matrix. The actual iteration in terms of the x values (scalars) takes the form; 1 11 11 11 in kk i iijj jji ii iiii bk ijj x ax ax aa a k N U B B k (2) 11 1kk XLDUXLD 11 21kk XLDUXLD 1 21 1kk k X XLDUXX In other words, 1 1kk ELDU E (4) For a convergent Gauss-Seidel iteration, the differ- ences in x values Ek written in terms of the difference between consecutive vectors of x values in Equation (4) above converges to the zero difference vectors when the solution X vector is reached. Denoting by M the iteration matrix; 1 M LD U and the difference vector of X among consecutive steps of the iteration by: 012 1 ,, ,, ,, kk EEE EE 1kk EME Assuming that the initial difference in x values (here after termed the error vector) E0 can be written as a linear combination of the Eigen vectors 12 ,, N vvv of the itera- tion matrix M of size N with corresponding Eigen values 12 ,,, N in decreasing order of magnitude where 1 is the dominant Eigen value: 01 112233 10112233 1111222333 1112223 33 111 1111222333 oN NN NNN kkk k kN kkk k kN EXXcvcvcvcv EMEc MvcMvcMvcMv Ecvcvcvc v Ecvcvcvc v Ecvcvcvc v 1 N NN NN For the Gauss-Seidel iteration the vector of x values is successively computed from the fixed-point iteration process by: 11 1kk XLDUXLDBMX (3) where the matrix is the iteration matrix and . 1 LDM 1 DB NL Taking the ratio of the Euclidean norms of Ek and Ek+1; 12 222 2 111 1 111222333 1 12 222 2 1112223 33 12 22 11 2 13 2 1112233 11 1 kkk k NN N k kkk k kNN N kk kN NN cv c vcvcv E Ecvc vcvcv cvcvcvc v 2 1k 12 22 23 2 111 2233 11 1 kk k kN NN cvcvcvcv 2  A. T. TIRUNEH 131 If 1 is the dominant Eigen value, then the ratios 2121 1 ,,, N tend to zero at higher k values so that 12 2 1 111 1 1 12 2 111 lim lim k k kk k k cv E Ecv (5) Therefore, for both converging and diverging Gauss- Seidel iterations, the error vector ratios are determined by the dominant Eigen value of the iteration matrix, 1. 2.1. Case I: Convergent Gauss-Seidel Iteration For a convergent iteration in which the dominant Eigen value is less than one, the difference vector Ek converges to zero. Denoting the estimate of the largest Eigen value of the iteration matrix M at the kth iteration by 1; and taking the difference among respective values of x as; 11kk ee Starting with the kth difference in x values among con- secutive steps of iteration, a geometric series is formed in terms of the e values; 23 11 1 ,, , kkkk ee e e The sum of this diminishing geometric series is given by (since 1 < 1); 1 1 ik i ik e e It is possible to write the e values so that; 1 12 23 kkk kkk kkk exx exx exx 1 2 So that; 1 1 ik ik ik e exx (6) Therefore, the solution x at convergence is extrapo- lated from Equation (6) above; 1 1 k k e xx (7) 2.2. Case II: Divergent Gauss-Seidel Iteration For a divergent Gauss-Seidel iteration, the error propaga- tion is studied as the iteration progresses. Let X0 be the initial estimate of the solution while Xs is the true solu- tion of the system of equation. The initial error vector Ero can then be written as: 0ro s EXX The difference between consecutive iteration values X is as defined before, i.e., 1kk EX X k The Gauss-Seidel iteration formula given in Equation (3), i.e., 11 1kk XLDUXLD B can also be rewritten as: 1kk X MX N where 1 LDM U is the iteration matrix as defined before and 1.DB NL The successive values of X of the iteration can now be written as follows; 10 0sr s ro sro X MXNM XEN M XNME XME The above expression is true because at the true solu- tion Xs, the Gauss-Seidel iteration satisfies the relation: ss X MX N Similarly for X2; 21 sro XMXNMXME N 22 2 s ro sro X MXNMEXM E Proceeding similarly at the kth iteration, the X-values can be written as: k ks XXME ro (8) Interms of the difference between consecutive x-esti- mates, recalling the formula derived earlier in Equation (4), i.e., 1 1 23 1 00 0000 1 00 0 kkk k k ki ki ELDUEME X XEMEMEME ME XX ME (9) It is seen from Equations (8) and (9) above that the X values increase in proportion to the iteration matrix M. Representing this increase in proportion to M by the largest Eigen value of the iteration matrix, 1, Equations (8) and (9) can now be written as: 110 kk ks ross X XEX XX (10) 101 0100 01 1 1 k ki ki E XX EX (11) Open Access JAMP  A. T. TIRUNEH 132 The expression in Equation (11) above is derived us- ing the general geometric series sum formula for an ex- panding geometric series. Equating the expressions for Xk in Equations (10) and (11): 01 10 0 1 1 1 k k ss E XXXX 01 10 1 1 11 k ks E XX 00 0 11 11 s EE XX 0 0 1 1 s E XX In general for iteration estimation made from the kth it- eration vales of xk and individual ekvalues the formula can be written as: 1 1 k sk e xx (12) It can be seen, therefore, that the same formula used for extrapolating a convergent Gauss-Seidel iteration can be used to extrapolate the solution from the divergent Gauss-Seidel iteration. Such a procedure which is un- conventional works well as the examples that follow il- lustrate. 2.3. Higher Order Aitken Extrapolation For the first-order Aitken extrapolation, the ratio of the norms of the error vector was shown in Equation (5) to be equal to the dominant Eigen value of the iteration ma- trix, i.e., 12 2 1 111 1 12 2 111 k k k k cv E Ecv For the second order Aitken extrapolation, the ex- trapolation made at the kth and (k + 1)th iterations are con- sidered: 1 1 1 1 1 k k sk E XX 1 11 1 1 1 1 k k sk E XX The second order error in terms of the extrapolated X vectors can be written as: 211 1 11 1 1 11 1 21 1 11 Δ 1 ksk sk kk kk k kk EX X EE XX E EE Similarly for the (k + 1)th iteration; 1 21 1 11 1 Δ 1 k kk E EE At the kth iteration, the ratio of the norm of the error vector becomes; 1 11 21 1 1 1 1 1 Δ 1 Δ 1 k k k kk k E E E EE E (13) In terms of the Eigen values and Eigen vectors v of the iteration matrix M, the terms in the norm expression of Equation (13) above are given by: 1 1112 223 33 kk k kN Ecvcvcvcv k NN 1 NN v 1111 1111222333 kkk k kN Ecvcvcvc 111 1 11112222 33 33 Δ 11 11 kk k kk kk Nn NN EEE cvc v cvc v 111 121 11 11112222 11 333 3 Δ 11 11 kkk kk kk NnN N EEE cvc v cvc v Collecting the terms for both the numerator and de- nominator yields, 1 1 11 11 11 1 1 1 1 1 Δ1 1 11 1 Δ11 1 k N ki kii i i kNi kii i ki E Ecv Ecv E (14) Examination of the terms on the right hand side of Equation (14) above reveals that the first terms of the summation (i.e. i = 1) in both the numerator and de- nominator vanish. Therefore, the second-order Aitken extrapolation reduces the Eigenvalue so that 2 becomes the dominant Eigen value. As will be shown below, the second dominant Eigen value of the iteration matrix, 2, will be equal to the ratio of the error vectors for the sec- ond order Aitken extrapolation. Factoring out the 2 term in Equation (14) above will Open Access JAMP  A. T. TIRUNEH Open Access JAMP 133 result in the following expression: 1 112 112223 1 12 1 1 12 222 3 1121 1 1 Δ11 11 1 Δ1 1 11 111 k N kii kii i k k N kkii kii i Ecvc v E E Ecvc v 1 Once 1 has been eliminated and 2 is the dominant Eigen value, the ratios: 1 22 ,3,4, kk ii i 5, being less than one, will vanish at higher k values so that the error norm ratios become 1 11 12 21222 11 1 1 12 222 1 1 2 1 2 Δ1 1 11 1 Δ11 1 k k k k kk k k k k E Ecv E EEcv E E E Similarly, it is easy to show that for the third and higher order Aitken extrapolations the error vector ratios correspond to the ith Eigen value of the iteration matrix. The higher order decomposition of Eigen values through higher order Aitken extrapolation can be generalized as: 1 for 1,2,3,, i ki k Ei E N k (15) In effect, higher order Aitken extrapolation succes- sively decomposes the dominant Eigen values so that the error terms are determined eventually by the lowest Ei- gen value of the iteration matrix. This works for both the convergent and divergent Gauss-Seidel iteration. How- ever, the procedure is best in decomposing the first two dominant Eigen values beyond which the decomposition might be slow or inexact due to the successively small difference in the error vectors. The examples that follow later for diverging Gauss-Seidel iteration illustrate this fact. 2.4. Coupling of SOR Technique with Geometric Series Extrapolation Theextrapolation to the Gauss-Seidel iteration can well be extended to the successive over relaxation (SOR) method. In matrix form, the SOR iteration process is: 1 1 1 1 k X DL UDX DL B (16) where is the relaxation factor and the other terms are as deifned above. The iteration matrix is the coeffic the Xk term in Equation (16) above and is given by ient of : 11 M DL UD (17) The iteration formula for the successive over relaxa- tion technique in terms of individual x values is given by; k1 11kk k xxbaxax (18) The acceleration factor cannot be easily determined in advance. It depends on the coefficient matrix A. If the coefficient matrix A is symmetric as well as pos definite, the spectral radius of the iteration matrix w mentioned ea ex t 1, 2, , ii iijjijj ji ji ii a in itive M ill be less than one—ensuring convergence of the proc- ess—when the value lies between 0 and 2. The procedure for extrapolation of the SOR process using geometric series sum, based on the dominant Eigen value of the iteration matrix as a ratio of the geometric series, follows a similar process to the one rlier. The only change is in the iteration matrix which is modified by the relaxation factor while the condition for convergence (i.e. the dominant Eigen value of the iteration matrix being less than one) remains the same. However, it should be noted that the optimum relaxa- tion factor is not necessarily the same as the SOR- optimum when the SOR technique is combined with Aitken extrapolation. This is illustrated in the application ample of the heat flow problem presented in this paper. The opt for the SOR techniques is so chosen that the two dominant Eigen-values become equal in magnitude and these Eigen values at the optimum can be complex numbers leading possibly to the failure of extrapolation methods. The fact that, at the optimum value of the ac- celeration factor , the dominant Eigen values turn out to be complex numbers is also shown in the heat flow ex- ample presented in this paper. Coupling the SOR tech- nique with the Aitken extrapolation at the exact optimum is not necessary as the result is not very sensitive to the value as will be shown in the heat flow example that follows. However, failure is not necessarily always the case for coupling at the optimum value. The applica- ion example suggests that in the case of coupling of  A. T. TIRUNEH 134 S The first example below is a simple 2 × 2 equation in x eidel iteration starts at values distant from the solution, i.e. the starting values of x = 10,000 and y = 4250. The x and y values of the eration, differences in consecutive steps of the iteration e and the ratios, , are co ue of the iteration ma- tri to −0.5). Therefore, the second x value, i.e., x OR with Aitken’s extrapolation, the value can be chosen so that it is slightly less than the SOR optimum value enabling the coupling to be made at real Eigen values without the method failing to lead to convergence to the solution. 3. Examples from Convergent Iterations 3.1. Example 1 and y values. 27xy 2xy The Gauss-S it i mputed and shown in Table 1. It is clear that the ratios of differences in x and y val- ues converge almost immediately to −0.50 for both the x and y values of the iteration. It will be later shown that, this value is the largest Eigen-val x, M. For calculating the extrapolated x value of the itera- tion, x = 10,000 cannot be used as the x0 value since the ratio at this level (−0.26) is not sufficiently convergent (compared 1 = −2125.5 is taken. For this value the 0 x e value is listed in Table 1 as 3186.75. For the y iteration y0 = 4250 can be taken as the ratio converged immediately with the first iteration. The value is also taken to be −6373.5. 0 y The x and y values are calculated as; e 0 0 3186.75 2121.5 3.000 110.5 x x e xx 0 0 6373.5 4250 1.000 110.5 y y e yy These values as expected are exactly equal to the solu- tion of the equations. To see that the ratios of alternative differences are the same as the largest Eigen value of the iteration matrix, the equation: 27 2 xy xy is written as A XB ; 21 7 11 2 x y Using the relation A = L + D + U 21002001 ;; ; 11 100100 ALDU ion of the Gauss-Seidel iteration for the 2 by 2 equation. Consecutive Difference ei (y) Ratio ei+1/ei (x) Ratio ei+1/ei (y) It can be shown that using the L, D and U matrices; Table 1. Computation for geometric series extrapolat Iteration Step x y Consecutive Difference ei (x) 0 10000.00 4250.00−12121.50 −6373.50 −0.26 −0.50 1 50 1025 1065 −2121.50 −2123.503186.75 3186.75 −0.50 −0. 2 65.3.2−1593.38 −1593.38 −0.50 −0.50 3 −528.13 −530.13796.69 796.69 −0.50 −0.50 4 268.56 266.56−398.34 −398.34 −0.50 −0.50 5 −129.78 −131.78199.17 199.17 −0.50 −0.50 6 69.39 67.39 −99.59 −99.59 −0.50 −0.50 7 −30.20 −32.2049.79 49.79 −0.50 −0.50 8 19.60 17.60 −24.90 −24.90 −0.50 −0.50 9 −5.30 −7.30 12.45 12.45 −0.50 −0.50 10 7.15 5.15 −6.22 −6.22 −0.50 −0.50 11 0.93 −1.07 3.11 3.11 −0.50 −0.50 12 4.04 2.04 −1.56 −1.56 −0.50 −0.50 13 2.48 0.48 0.78 0.78 −0.50 −0.50 14 3.26 1.26 −0.39 −0.39 15 2.87 0.87 −2.87 −0.87 Open Access JAMP  A. T. TIRUNEH 135 1012 012 LDU and that 1012 012 MLDU The Eigen values of the iteration matrix M matrix are solving the determinant equation; found by 012 det 0 1 02 MI 10 2 1 0 or 0. 2 The largest Eigen value is −0.5 and it can be seen from Table 1 that the ratios of consecutive differences for both x and y variables converge to the largest Eigen value of the iteration matrix. 3.2. Ex n vector is The iteration starts with the uss-Seidel iteration was carried out 13 times at which level four decimal-digit accuracy was obtained for thrences in x, y and z values. Ts and ratios of consecutive e values. can be shown that the iteration matrix M is given by; ample 2 The 2nd example is a 3 × 3 systems of linear equations given below 35 23 4 42 xyz xz xyz The solutioT , , 1, 1, 1xyz vector: TT ,,10,8,5xyz The Ga e ratio of consecutive diffe able 2 shows the corresponding x, e value It is shown in Table 2 that, with the geometric series extrapolation a 5 digit accuracy has been obtained for the solution with just 9 iterations. The normal Gauss-Seidel iteration requires more than 60 iterations to arrive at 5 digit accuracy. For the coefficient matrix A of the given equation, it 1 11 0 33 110 066 82 MLDU The Eigen values are found by solving the determinant; 11 0 11 033 110 det 00 66 11 082 MI 221 0 38 0,0.1525793240.81924599or Therefore, the largest Eigen value of the iteration ma- trix M is = −0.81924599 and all the ratios used above were approaching towards the largest Eigen value of the iteration matrix accurate to 5 digits as shon in Table 2. 3.3. Applicat steel plate with dimension 10 × 20 cm has one of its 10 e w ion Example (Heat Flow Problem) Example of application of the Aitken extrapolation me- thod for a steady state heat flow problem involving Laplace equation is given below [15]. A rectangular thin cm edges held at 100˚C and the other three edges ar held at 0˚C. The thermal conductivity is given as k = 0.16 cal/sec·cm2·˚C/cm. Figure 1 shows the steel plate steady state conditions temperatures. The steady state heat flow problem is described by the Laplace equation: 22 22 0 uu xy with the boundary conditions, ,0,100,0 and 20,100Cuxuxu yuy . The nine-point finite difference formula of the Laplace equation is used for computation. is formula is sym- bolically represented by: ss- equation after 9 iterations. Rat Th Table 2. Results geometric series extrapolation of the Gau Values after 9 iterations Differences in values Seidel iteration for the 3 by 3 ios of differences Extrapolated values x0 = 1.44846653 0 x e= −0.81586443 x = −0.81923923 x = 1.000001908 y0 = 1.79206166 y = −0.81924816 y = 0.999998918 0 y e = −1.44095868 z0 = 1.31013205 0 z e = −0.56420578 z = −0.81924493 z = 1.000000209 Open Access JAMP  A. T. TIRUNEH 136 2 , 6 ij u h , 0 ij u 2 14 14204 141 The ahe differen 1 lgebraic form of tce equation is: 1,1 1,1 1,11,1 2 1,1,, 1, 1, 1 6 44 44 20 ij ij ijij i ji jijijij uuuu h uu u uu 0 wpera- tures at the intersection of the rectangular grid lines. Using a grid size of 2.5 cm, the 21 interior grid points shown in Figure 2 are generated. The coefficient matrix A of the linearized form of the Laplace equation AU = B by finite differencing is given near sy itially. In addition the ge h ions for the ndel itera- ton ed. In addition torms of ts for each step oere com- peometric series addition tctors and normctors, the consecutive difference ratios, as appn of the between 2.1 an here h is the grid size and the u values are the tem in Table 3, followed by the right hand side vector B. A MATLAB program was written to solve the li stem of equations for the 21 unknown temperatures using the Gauss-Seidel iteration in ometric series extrapolation of the Gauss-Seidel was computed by writing the corresponding program in the MATLAB environment. The solution vector X for eac of the 100 iteratormal Gauss-Sei iwas comput he error vector he Euclidian n f the iteration w uted. For the gextrapolation, in o the solution ve of the error ve roximatio maximum Eigen-value were also computed. Figure 3 shows a comparison of the number of itera- tions required to arrive at more or less the same magni- tude of the norm of the error vector for the normal Gauss-Seidel iteration and for the extrapolation. It is ob- served from Figure 3 that the extrapolation procedure will give an acceleration factor in the range d 2.2. For example whereas 16 iterations are required for the normal Gauss-Seidel iteration giving error norm of 0.06+ , the geometric series extrapolation required only 7 iterations. For the subsequently smaller error norms, the numbers of iterations required are in the ratio of 16/7, 18/8, 20/9, 22/10, 24/11. It is clear that as the error norm gets smaller, the acceleration factor approaches a value of 2. The right hand side vector of the finite difference equation is given as: T ,0, 600,0,0,0,0,0,0, 550 0,0,0,0,0,0, 550,0,0,0,0B,0 Figure 1. Rectangular plate for the steady state heat flow problem with boundary conditions. Figure 2. Rectangular plate for the heat flow problem with interior points and boundar y conditions shown. Open Access JAMP 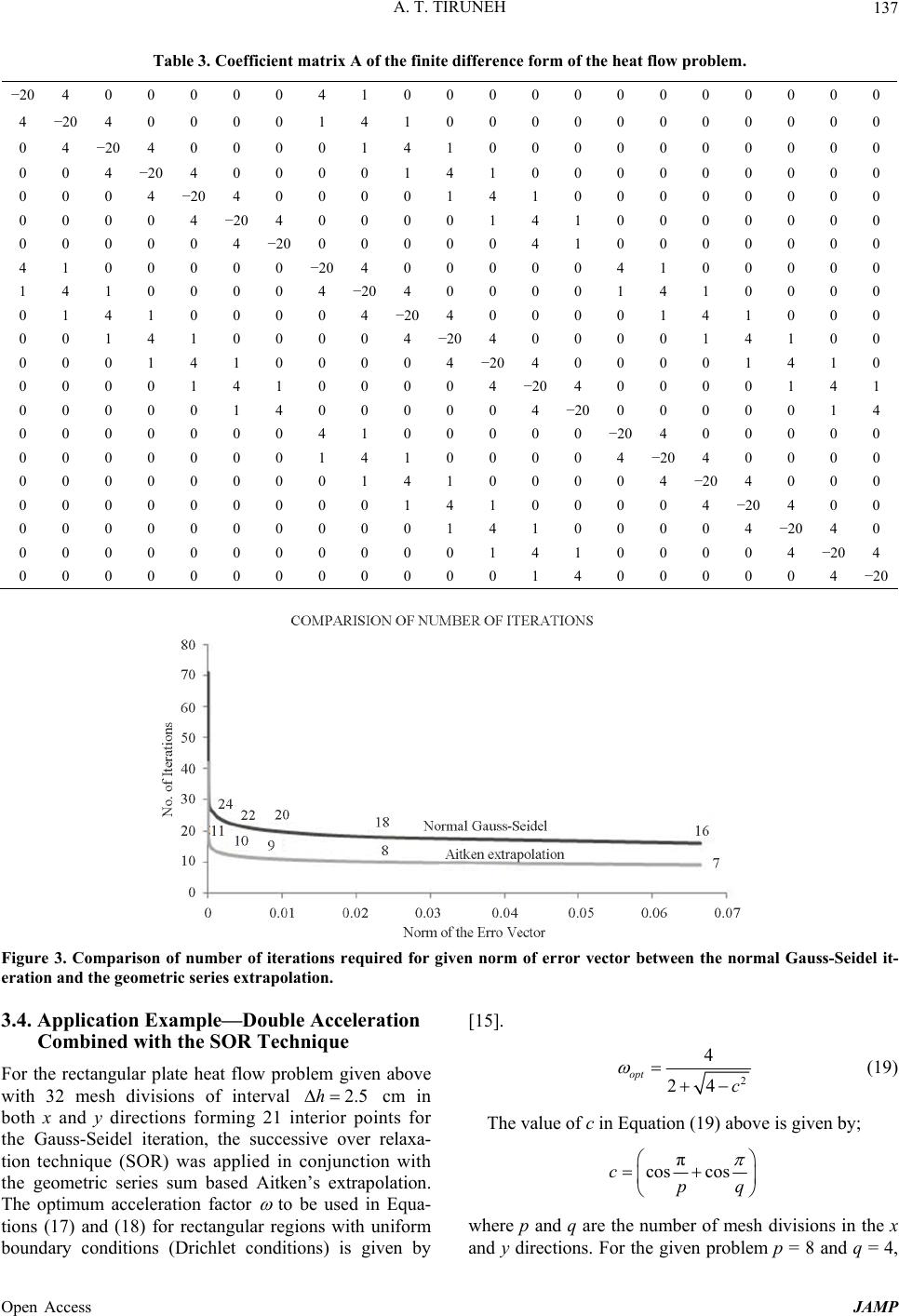 A. T. TIRUNEH 137 Table 3. Coefficient matrix A of the finite difference form of the heat flow problem. −20 4 0 0 0 0 0 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 4 0 0 0 0 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 4 0 0 0 0 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 4 0 0 0 0 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 4 0 0 0 0 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 4 0 0 0 0 1 4 1 0 0 0 0 0 0 0 0 0 0 0 0 4 −20 0 0 0 0 0 4 1 0 0 0 0 0 0 0 4 1 0 0 0 0 0 −20 4 0 0 0 0 0 4 1 0 0 0 0 0 1 4 1 0 0 0 0 4 −204 0 0 0 0 1 4 1 0 0 0 0 0 1 4 1 0 0 0 0 4 −204 0 0 0 0 1 4 1 0 0 0 0 0 1 4 1 0 0 0 0 4 −204 0 0 0 0 1 4 1 0 0 0 0 0 1 4 1 0 0 0 0 4 −204 0 0 0 0 1 4 1 0 0 1 0 0 0 0 1 4 − − − − − − − 0 0 0 1 4 1 0 0 0 0 4 −204 0 0 0 0 1 4 0 0 1 4 0 0 0 0 0 4 −200 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4 1 4 1 0 1 0 0 0 0 0 0 0 0 4 204 20 0 4 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 0 0 0 0 4 204 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 0 0 0 0 4 20 4 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 0 0 0 0 4 20 4 0 0 0 0 0 0 0 0 0 0 0 0 1 4 1 0 0 0 0 4 204 0 0 0 0 0 0 0 0 0 0 0 0 1 4 0 0 0 0 0 4 20 Figure 3. Comparison of number of iterations required for given norm of error vector between the normal Gauss-Seidel it- eration and the geometric series extrapolation. 3.4. Application Example—Double Acceleration Combined with the SOR Technique For the rectangular plate heat flow problem given above with 32 mesh divisions of interval cm in both x and y directions forming 21 interior points for the Gauss-Seidel iteration, the successive over relaxa- tion technique (SOR) was applied in conjunction with the geometric series sum based Aitken’s extrapolation. The optimum acceleration factor to be used in Equa- tions (17) and (18) for rectangular regions with uniform boundary conditions (Drichlet conditions) is given by [15]. 2.5h 2 4 24 opt c (19) The value of c in Equation (19) above is given by; π cos cosc p q where p and q are the number of mesh divisions in the x and y directions. For the given problem p = 8 and q = 4, Open Access JAMP 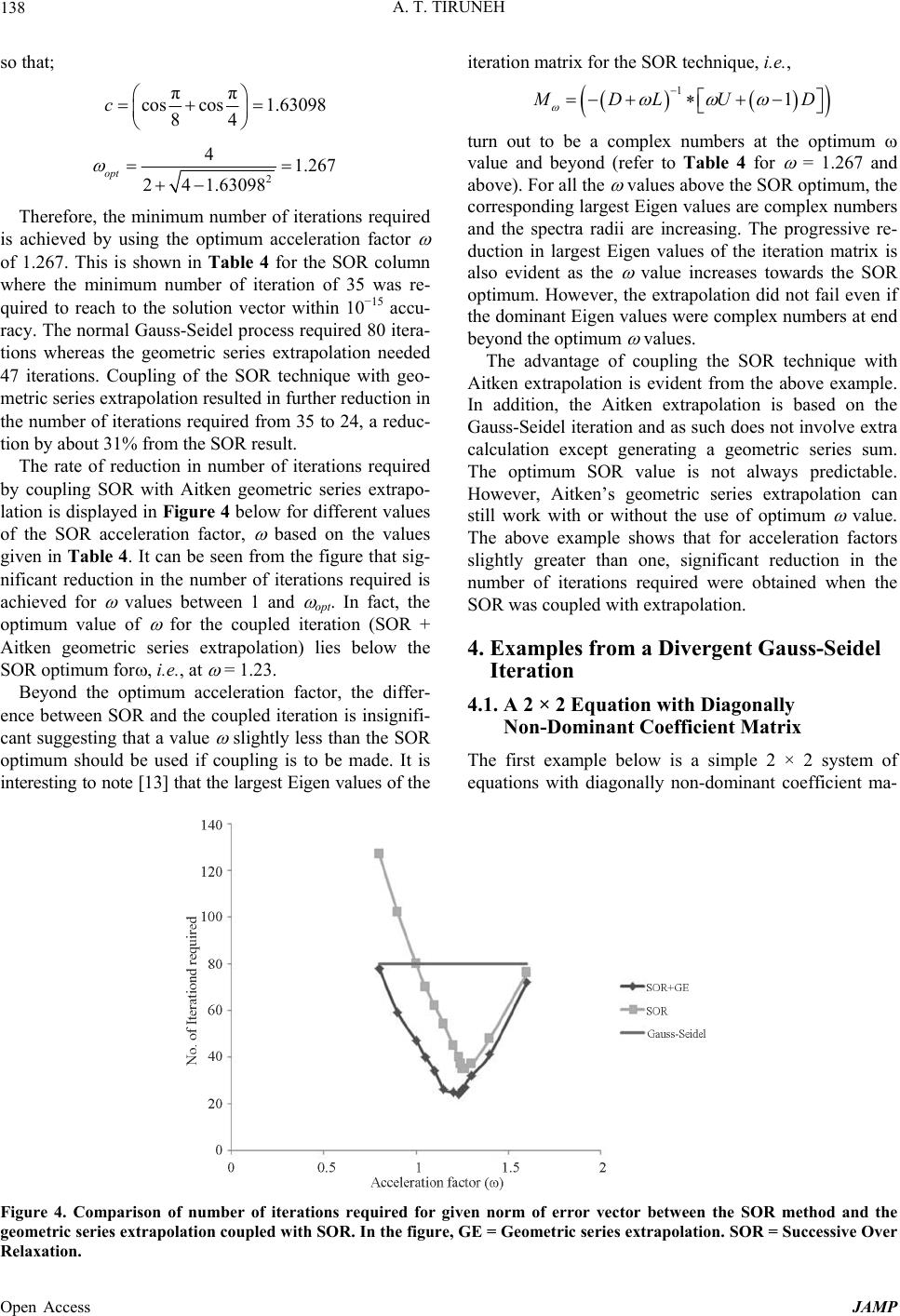 A. T. TIRUNEH 138 so that; ππ cos cos1.63098 84 c 2 41.267 241.63098 opt Therefore, the minimum number of iterations required is achieved by using the optimum acceleration factor of 1.267. This is shown in Table 4 for the SOR column where the minimum number of iteration of 35 was re- quired to reach to the solution vector within 10−15 accu- racy. The normal Gauss-Seidel process required 80 itera- tions whereas the geometric series extrapolation needed 47 iterations. Coupling of the SOR technique with geo- 4, a reduc- by c extrapo- d on th etween SOR and the coupled iteration is insignifi- cant suggesting that a value slightly less than the SOR optimum should be used if coupling interesting to note [13] that the largest Eigen values of the iteration matrix for the SOR technique, i.e., metric series extrapolation resulted in further reduction in the number of iterations required from 35 to 2 tio by about 31% from the SOR result. The rate of reduction in number of iterations required oupling SOR with Aitken geometric series n lation is displayed in Figure 4 below for different values of the SOR acceleration factor, basee values given in Table 4. It can be seen from the figure that sig- nificant reduction in the number of iterations required is achieved for values between 1 and opt. In fact, the optimum value of for the coupled iteration (SOR + Aitken geometric series extrapolation) lies below the SOR optimum for, i.e., at = 1.23. Beyond the optimum acceleration factor, the differ- ence b is to be made. It is 11 M DL UD turn out to be a complex numbers at the optimum value and beyond (refer to Table 4 for = 1.267 and above). For all the values above the SOR optimum, the corresponding largest Eigen values are complex numbers and the spectra radii are increasing. The progressive re- duction in largest Eigen values of the iteration matrix is also evident as the value increases towards the SOR optimum. However, the extrapolation did not fail even if the dominant Eigen values were complex numbers at end beyond the optimum values. The advantage of coupling the SOR technique with Gauss-Seidel iteration and as such does not involve extra 2 × 2 system of eq Aitken extrapolation is evident from example. In addition, the Aitken extrapolation is based on the the above calculation except generating a geometric series sum. The optimum SOR value is not always predictable. However, Aitken’s geometric series extrapolation can still work with or without the use of optimum value. The above example shows that for acceleration factors slightly greater than one, significant reduction in the number of iterations required were obtained when the SOR was coupled with extrapolation. 4. Examples from a Divergent Gauss-Seidel Iteration 4.1. A 2 × 2 Equation with Diagonally Non-Dominant Coefficient Matrix The first example below is a simple uations with diagonally non-dominant coefficient ma- Figure 4. Comparison of number of iterations required for geometric series extrapolation coupled with SOR. In the figu Relaxation. given norm of error vector between the SOR method and the re, GE = Geometric series extrapolation. SOR = Successive Over Open Access JAMP  A. T. TIRUNEH 139 Table 4. Comparison of number of iterations required between with the SOR technique. w SOR + GE SOR Extra acceleration Normal SOR and Aitken’s geometric series extrapolation coupled Largest Eigen value of the SOR iteration matrix 0.8 78 127 1.63 80 0.859905 0.9 59 102 1.73 80 1 47 80 1.70 80 1.05 40 70 1.75 80 1.1 34 62 1.82 80 1.15 26 54 2.08 80 1.2 25 45 0.827175 0.788581 1.23 24 40 1.67 80 1.25 26 35 1.35 80 1.267 27 35 1.30 80 0.760252 0.729593 0.691062 0.637938 1.80 80 Complex number 1.24 25 37 1.48 80 Complex number 1.3 32 37 1.16 80 Complex number 1.4 41 48 1.17 80 Complex number 1.6 72 76 1.06 80 Complex number 1.8 298 168 0.56 80 Complex number 0.59002 0.532422 trix The Gauss-Seidel iteration starts at values of x = 8 and y = 10. The x and y values of the iteration, differences in consecutive steps of the iteration ei and the ratios, , were computed and are shown in Table 5. As Table 5 shows, the Gauss-Seidel based iteration diverges as the atrix. However, the Aitken ex- trapolatios (shons o tab innvo tx = y ng the es of econd iteration in Tab l e 5, the extra y val, xs and ysculated using Eqtion (12; 210 12 15 510 xy xy coefficient matrix is also diagonally non-dominant. This is also evident from the ratio of differences in x and y values shown in Tabl e 5. This ratio is −15 for both x and y iterations and it corresponds to the dominant Eigen value of the iteration m n iteration variably co wn in erge t the last colum he true solutions f the 1 and le) = 1. Usi polated valu x and the s ues are cal ua) as 0 0 10 676 1.000 11 x sx e xx 800 15 0 0 32 1.000 11 y sy e yy se valus exped are exactly equal to the s tion of the equations. 4.2. A 4 × 4 Equations with Diagonally Non-Dominant Coefficient Matrix A second example of a four by four system of equations in which the coefficient matrix is once again diagonally non-dominant is presented below. 400 2026 15 The es acteolu- 1 2 3 20234 12320783 13656120 125346 123 1207625127 x x x 4 20 125 14520481 x The normal Gauss-Seidel iteration quickly diverges as such. Higher order Aitken extrapolation has to be carried out sin matrixfifth or- der Aitken extrapolatissfully achieves conver- gence whereas the firstinant Eigen values were successfully decomposed with and second order Aitken extrapolations rely. The solution of the s equations together with the Eigen values of the iteration matrix for the Gauss- Seidel iteration as obta program are given in Table 6. Figure 5 shows the sition of error ratios for the five-order Aitken extrtion. Comparing the ra- tio of successive errors t each level of extrapola- tion with the Eigen values of the iteration matrix given expected and it is not possible to reach to the solution as ce the two dominant Eigen values of the iteration are large (16.7 and 5.77 respectively). A on succe two dom the first spective ystem of ined using MATLAB decompo apola given a Open Access JAMP  A. T. TIRUNEH 140 Table 5. Gauss-Seidel iteration results for a diagonally non-dominant and diverging 2 × 2 system of equations. Iteration Consecutive Difference ) Consecutive Difference ei (y) Ratio ei + 1/ei (x) RExtrapolation (X) Extrapolation (Y) Step x y ei (xatio ei + 1/ei (y) 0 8 10 −52 −144 −13.846 4.49 1 −15 1 − − 2160 −15 1 1 62026 00 −32400 −15 1 1 −10124 −30374 162000 486000 −15 1 1 15145 000 −7290000 −15 1 1 −22 −64 0 1.09 × 108 −15 1 1 1876 102515626 −5.5E+08 −1.6 × 109 1 −5.1 × 108 −1.538 × 109 8.2 × 1009 2.46 × 1010 8 7.69 ×109 2.3066 × 10101.2 × 1011 −3.7 54 5.2 × 1012 44 134 720−15 2 76 −108 −15 3 −15 4 876 5626−2430 −15 5 7812483437 3645000−15 6 3417−15 −15 1 7 −15 −15 1 1 × 1011 −15 −15 1 1 × 1012 − 9 −1.2 × 1011 −3.46 × 1011 1.85 × 1012 5. 10 1.73 × 1012 5.1899 × 1012 −1.7 × 1012 − Table 6. Values of solution to the four by four system of equa program. Solutions of the systems of equation tions and Eigen values of the iteration matrix using MATLAB Eigen values of the iteration matrix X1 = 3.054225004761563 −16.700300071436452 X2 = −2.904223059942874 X3 = −0.661832433353327 X4 = −4.154545738306979 5.774221605390342 0.085523954767930 0 Figure 5. Variation of ratos of the error vectors at 1st to 5th oenapolation in ble 6ve shoat the first dominant Ei- gen valuesdecomd exactly −16.7003 and 2 = 5.7742). How the 3igher order extolasition slot eventually reduces stly g convef the itera- tion. F ur ss of rf the norm of the error vector computed from irder Aitk extr. Ta abows thtwo are pose ever, for (i.e. 1 = rd and h raption the decompows bu ufficien enablinrgence o ige 6 shows the progreeduction o EBAX As can be seenom Ta , with e fifth ord extrapolatthe no the erroector eveally down 0−9. Itld be recalled that tnor- mal Gauss-Seidel iteration is rapidly diverging for this m of equs. On tther hanigher order Ait- ken extrapolation as applied in this example successfully frble 7ther Ait- ken ion, rm ofr vntu reduces to 1 shouhe systeationhe od h Open Access JAMP 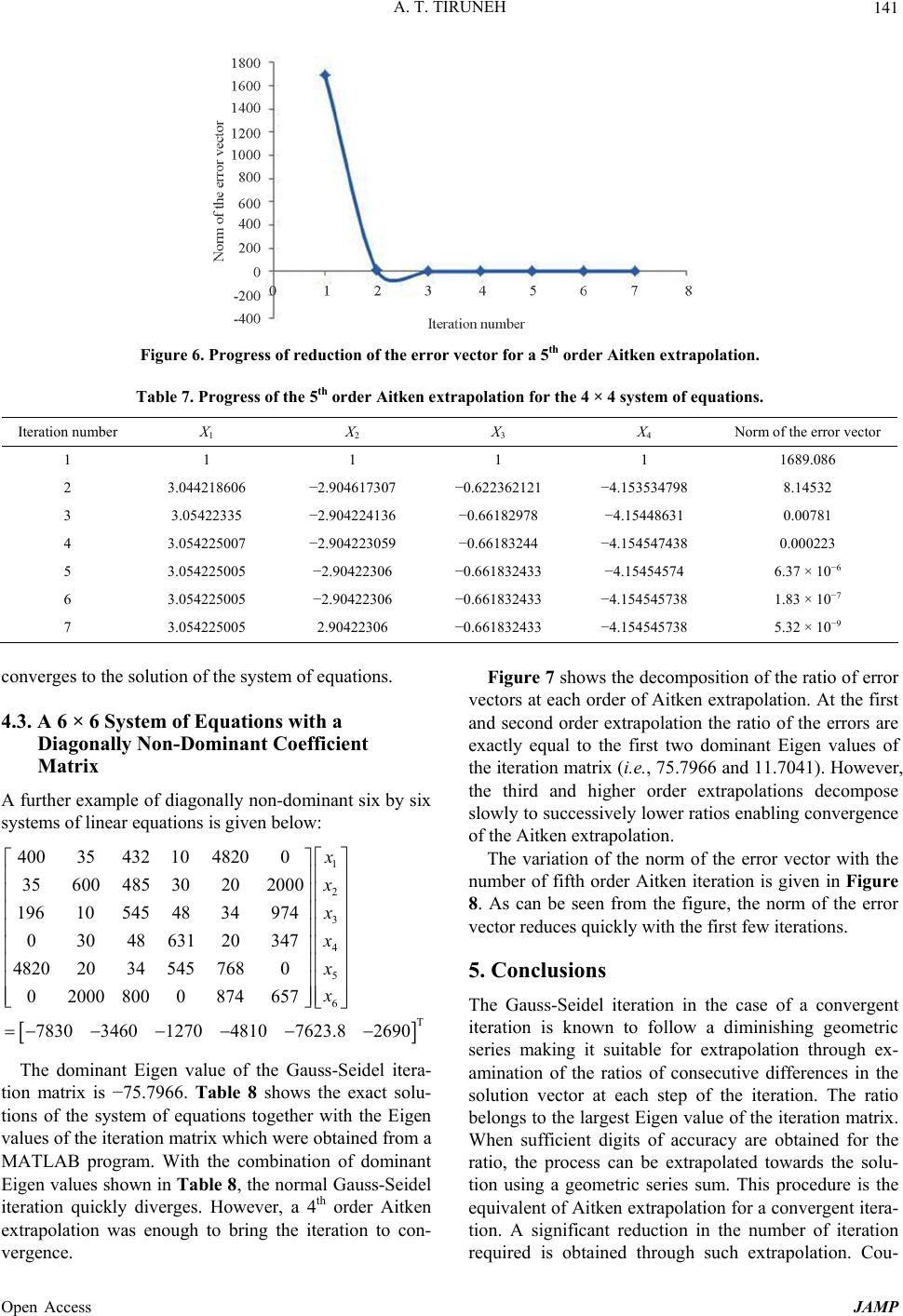 A. T. TIRUNEH 141 F duction of the error vector for a 5th ord. Table 7. Progress of the 5th order Aitken extrapolation for the 4 ns. Iteration number X2 X3 rm of the error vector igure 6. Progress of reer Aitken extrapolation × 4 system of equatio X1 X4 No 1 1 1 1 1 1689.086 2 3.044218606 −2.904617307 0.622362121 −4.153534798 8.14532 3 3.05422335 −2.904224136 −0.66182978 −4.15448631 0.00781 4 3.054225007 −2.904223059 −0.66183244 −4.154547438 0.000223 5 3.054225005 −2.90422306 −0.661832433 −4.15454574 6.37 × 10−6 6 3.054225005 −2.90422306 −0.661832433 −4.154545738 1.83 × 10−7 7 3.054225005 2.90422306 −0.661832433 −4.154545738 5.32 × 10−9 − converges to the solution of the system of equations. 4.3. A 6 × 6 System of Equations with a Diagonally Non -D ominant Coefficient Matrix A further example of diagonally non-dominant six by six systems of linear e The dominant Eigen value of the Gauss-Seidel itera- tion matrix is −75.7966. Table 8 shows the exact solu- tions of the system of equations together with the Eigen values of the iteration matrix which were obtained from a MATLAB program. With the combination of dominant Eigen values shown in Table 8, the normal Gauss-Seidel iteration quickly diverges. However, a 4th order Aitken extrapolation was enough to bring the iteration to con- vergence. Figure 7 shows the decomposition of the ratio of error vectors at each order of Aitken extrapolation. At the first and second order extrapolation the ratio of the errors are exactly equal to the first two dominant Eigen values of the iteration matrix (i.e., 75.7966 and 11.7041). However, the third and higher order extolations decompose ling convergence The variation of the norm of the error vector with the number of fifth order Aitken iteratio is given in Figure 8. series making it suitable for extrapolation through ex- amination of the ratios of consecutive differences in the solution vector at each step of the iteration. The ratio belongs to the largest Eigen value of the iteration matrix. When sufficient digits of accuracy are obtained for the ratio, the process can be extrapolated towards the solu- tion using a geometric series sum. This procedure is the equivalent of Aitken extrapolation for a convergent itera- tion. A significant reduction in the number of iteration required is obtained through such extrapolation. Cou- quations is given below: slowly to successively lower ratio enab of the Aitken extrapolation. 6 T 02000 8000874657 7830 3460 1270 4810 x 1 2 3 4 5 40035432 1048200 35600485 30202000 196 105454834974 03048 63120347 48202034 5457680 x x x x 7623.8 2690 x rap s n As can be seen from the figure, the norm of the error vector reduces quickly with the first few iterations. 5. Conclusions The Gauss-Seidel iteration in the case of a convergent iteration is known to follow a diminishing geometric Open Access JAMP 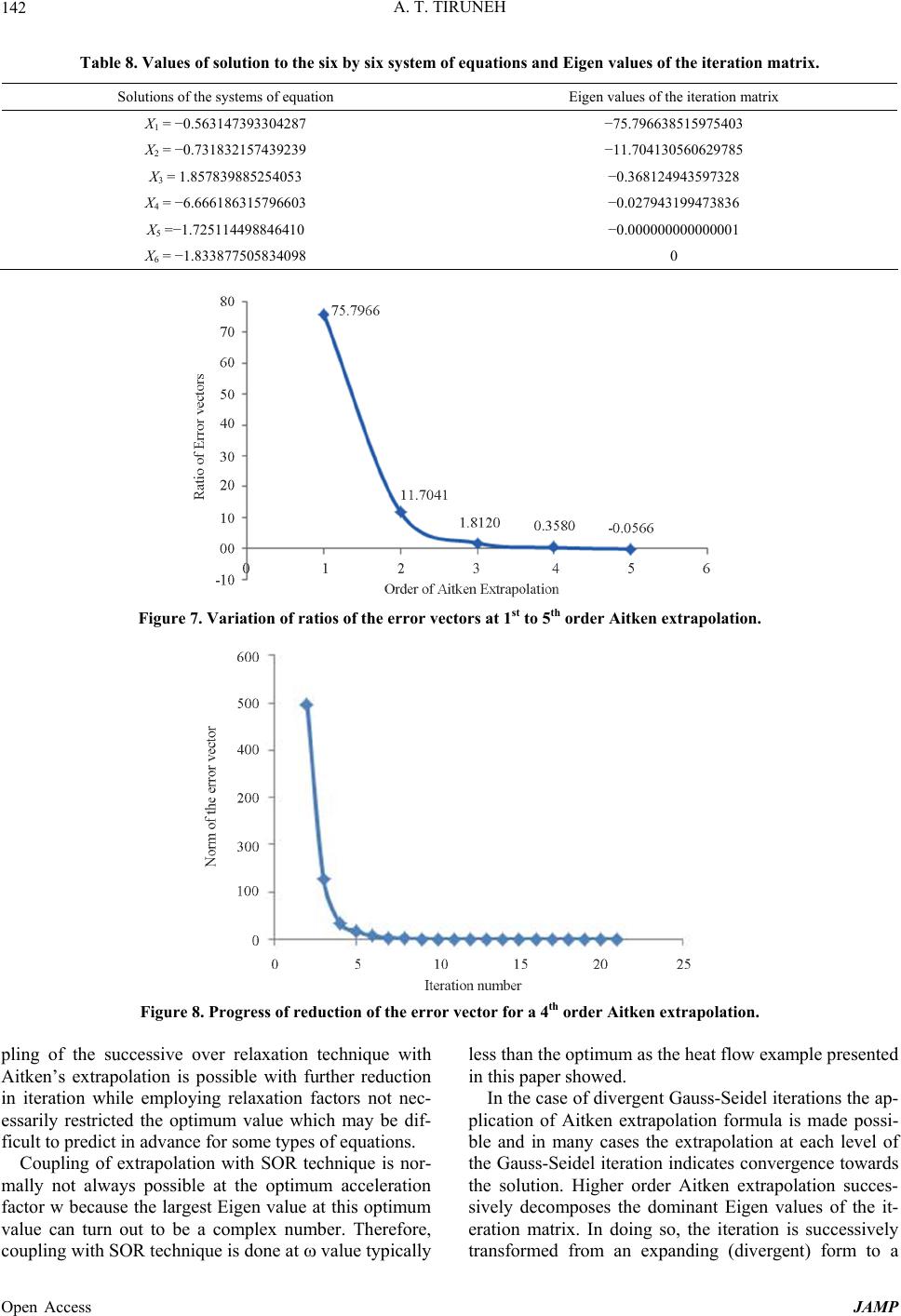 A. T. TIRUNEH 142 Table 8. Values of solution to the six by six system of equations and Eigen values of the iteration matrix. Solutions of the systems of equation Eigen values of the iteration matrix X1 = −0.563147393304287 −75.796638515975403 X2 = −0.731832157439239 −11.704130560629785 X3 = 1.857839885254053 −0.368124943597328 X4 = −6.666186315796603 −0.027943199473836 X5 =−1.725114498846410 −0.000000000000001 X6 = −1.833877505834098 0 Figuion of raror vecth orderolation. re 7. Variattios of the ertors at 1st to 5 Aitken extrap ctor for a 4th order Aitken extrapolation. less than the optimum as the heat flow example pres Figure 8. Progress of reduction of the error ve pling of the successive over relaxation technique with Aitken’s extrapolation is possible with further reduction in iteration while employing relaxation factors not nec- es coupling with SOR technique is done at value typically ented . ergent Gauss-Seidel iterations the ap- sarily restricted the optimum value which may be dif- ficult to predict in advance for some types of equations. Coupling of extrapolation with SOR technique is nor- mally not always possible at the optimum acceleration factor w because the largest Eigen value at this optimum value can turn out to be a complex number. Therefore, in this paper showed In the case of div plication of Aitken extrapolation formula is made possi- ble and in many cases the extrapolation at each level of the Gauss-Seidel iteration indicates convergence towards the solution. Higher order Aitken extrapolation succes- sively decomposes the dominant Eigen values of the it- eration matrix. In doing so, the iteration is successively transformed from an expanding (divergent) form to a Open Access JAMP  A. T. TIRUNEH 143 stable convergent iteration. At each stage of the applica- tion of higher order Aitken extrapolation, the ratio of the error vectors (differences in successive x values) ap- proaches the dominant Eigen value for that order of ex- trapolation an interesting possibility of stabilizing, i.e., converting a divergent fixd convergent iteration. In genelate the solution from divergent as an interesting possibility that expe of application of fixed point iteratiohampered by problems of di [1] H. L. Stone, “Iterative Solution of Implicit Approxima- tions of Multidimensional Partial Differential Equations,” SIAM Journal on Numerical Analysis, Vol. 5, No. 3, 1968, pp. 530-558. http://dx.doi.org/10.1137/0705044 . Higher order Aitken extrapolation provides e point iteration to a stable, ral, the ability to extrapo Guss-Seidel iteration i ands further the scop n which in some cases is vergence. REFERENCES [2] M. R. Hestenes and E. Stiefel, “Methods of Conjugate Gradients for Solving Linear Systems,” Journal of Re- search at the National Bureau of Standards, Vol. 49, 1952, pp. 409-436. http://dx.doi.org/10.6028/jres.049.044 [3] G. H. Golub and C. F. Van Loan, “Matrix Computations,” 3 Edition, Johns Hopkins University Press, Baltimore, 1996. [4] J. C. West, “Preconditioned Iterative Solution of Scatter- ing from Rough Surfaces,” IEEE Transactions on Anten- nas and Propagation, Vol. 48, No. 6, 2000, pp. 1001- 1002. http://dx.doi.org/10.1109/8.865236 [5] A. C. Aitken, “Studies in Practical Mathematics. The Eva- luation of Lat Proceedings of the Royal Society of Edinburgh, Vol. 57, 1937, p. 269. 70, No. 12, 1987, pp. 2577-2584. s in Engi- un,” John Wiley [8] S. R. Capehelerating Iterative Me- thods for thical Problems,” Ph.D. DissertationOrsity, 1989. [9] P. Henrici, l Analysis,” John Wi- ley & Sons, [10] S. D. Kamv,. D. Manning and G. H. Golub, “Extrapolatiothods for Accelerating Page Rank Computations,” gs of the Twelfth Interna- tional World Wide Web Conference, 2003, pp. 261-270. http://dx.doi.org/10.1145/775152.775190 ent Roots and Latent Vectors of a Matrix,” [6] M. D. Gianola and L. R. Schaffer, “Extrapolation and Convergence Criteria with Jacobi and Gauss-Seidel Itera- tion in Animal Models,” ournal of Diary Science, Vol. J [7] B. Irons and N. G. Shrive, “Numerical Method neering and Applied Science: Numbers are F & Sons, New York, 1987. art, “Techniques for Acc e Solution of Mathemat , klahoma State Unive “Elements of Numerica New York, 1964. ar T. H. Haveliwala, C n Me Proceedin [11] C. Breziniski and M. R. Zaglia, “Generalizations of Ait- ken’s Process for Accelerating the Convergence of Se- quences,” Journal of Computational and Applied Mathe- matics, Vol. 26, No. 2, 2007, pp. 171-189. [12] A. Bjorck, “Numerical Methods in Scientific Comput- ing,” Linkoping University Royal Institute of Technology, Vol. 2, 2009. [13] D. M. Young, “Iterative Solution of Large Linear Sys- tems,” Academic Press, New York, 1971. [14] G. Dahlquist and A. Bjorck, “Numerical Methods,” Pren- tice Hall, Englewood Cliffs, 1974. [15] C. F. Gerald and P. O. Wheatley, “Applied Numerical Analysis,” 5th Edition, 1994. plied Iterative Me- thods,” Academic Press, New York, 1981. [16] L. A. Hageman and D. M. Young, “Ap Open Access JAMP |

