Energy and Power Engineering, 2013, 5, 914-921
doi:10.4236/epe.2013.54B175 Published Online July 2013 (http://www.scirp.org/journal/epe)
Branching Process based Cascading Failure Probability
Analysis for a Regional Power Grid in China with Utility
Outage Data
Hui Ren1, Ji Xiong1, David Watts2,3, Yibo Zhao4
1Department of Electrical Engineering, North China Electric Power University, Baoding, China
2Pontificia Universidad Catolica de Chile, PUC, Vicuna Mackena 4860, Macul, Santiago, Chile
3University of Wisconsin-Madison, Wisconsin, USA
4School of information & Electronic Engineering, Beijing Institute of Technology, Beijing
Received April, 2013
ABSTRACT
Studying the propagation of cascading failures through the transmission network is key to asses and mitigate the risk
faced the energy system. As complex systems the power grid failure is often studied using some probability distribu-
tions. We apply 4 well-known p robabilistic models, Poisson model, Power Law model, Generalized Poisson Branching
process model and Borel-Tanner Branching process model, to a 14-year utility historical outage data from a regional
power grid in China, computing probabilities of cascading line outages. For this data, the empirical distribution of the
total number of line outages is well approximated by the initial line outages propagating according to a Borel-Tanner
branching process. Also for this data, Power law model overestimates, while Generalized Possion branching process
and Possion mod el underestimate, the probability o f larg er outages. Especially, the pro bability distribution generated by
the Poisson model deviates heavily fro m the observed data, underestimating the probability of large ev ents (total no. of
outages over 5) by roughly a factor of 10-2 to 10-5. The ob servation is confirmed by a statistical test of model fitness.
The results of this work indicate that further testing of Borel-Tanner branching process models of cascading failure is
appropriate, and should be further discussed as it outperforms other more traditional models.
Keywords: Cascading Failure; Poisson; Power Law; Branching Process; Generalized Poisson; Borel-Tanner
1. Introduction
Cascading failure is the process by which initial outages
of components of the electric power transmission system
can occasionally propagate to more widespread outages
and large blackouts. These blackouts involve complex
chains of events, that are not completely independent, as
an outage that have already occurred weakens the system,
making the systems more vulnerable and further outages
more likely [1].
Since 2001, researchers with multiple backgrounds of
electrical engineering, mathematics, physics and nonlin-
ear dynamics have work more heavily addressing this
topic from different angles. This research on cascading
models is surveyed and presented in [2,3], and is mainly
focused on 1) studying on the evolution of cascading
failure from a long term point of view; 2) studying on the
effect of specific disturbances on cascading propagation;
3) identifying the vulnerable area of the system accord-
ing to the topological features; 4) evaluating hazards the
initial failure could cause to the system by id entifying th e
afterwards cascades being initiated. All these researches
provide helpful research results.
Dealing with these issues and performing risk assess-
ment requires often identifying the probability distribu-
tion of blackout size. It has been widely ob serv ed that the
probability distributions produced by models in above-
mentioned research works have approximate power law
regions that cannot be produced by independent outages
and are broadly consistent with the characteristics ob-
served in the utility historical outage data from several
countries.
Historical outage data has always been used to power
system reliability evaluation, considering it encompasses
the effect of both inadequacy and insecurity of the stud-
ied system. A bulk statistical approach based on the his-
torical outage data is different from traditional methods
of risk analysis that rely on detailed analysis of enumer-
ated interactions, and will be complementary to tradi-
tional methods, especially on the risk analysis of large
blackouts because of the challenges on computational
power faced by enumerated interaction methods [1] and

H. REN ET AL. 915
the difficulties addressing complexity and non-inde-
pendency among different events.
1.1. Probabilistic Models for Utility Outages
While the literature body in this field is very broad, this
section summarizes previous work on probabilistic mod-
els for utility outages that relates more closely to our
work.
Chen and McCalley, after analyzing the North Ameri-
can transmission line outaged data in [4], proposed an
accelerated propagation model for the number of trans-
mission line outages [5]. They try a generalized Poisson
distribution and a negative binomial distribution for the
accelerated propagation model. The fitness test of the
accelerated propagation model to the reference utility
outage data showed, for the PDF of the number of line
outaged, the proposed exponentially accelerated cascad-
ing model on the prob ability of ou tages with more than 6
lines fit better than other models (0.00061 for accelerated
propagation model, while 0.00053 for the observed out-
age data, probabilities produced by Generalized Poisson
model and Negative Binomial model are one order of
magnitude smaller that that of the observed data).
In [1], Ren and Dobson demonstrated a way to test a
branching process based bulk statistical model of cas-
cading line outages on industry data. The model de-
scribed the development of cascading failure starting
from initial outages that then propagates in stages. The
average amount of propagation was estimated and hence
the probability distribution of the size of the cascading
failure (measured by the total number of line outages)
was predicted. The fit of the model is examined with a
9-year historical outage data set from a regional power
grid. Furthermore, Dobson [6] improves the branching
process model in [1] by considering variant propagation
in different stages, modeling the increases of propagation
as the cascade proceed following the observation in the
utility data [8]. Th e branch ing process mod el is then used
to predict the distribu tion of total number of outages for a
given number of initial outages. They study how the total
number of lines outaged depends on the propagation as
the cascade proceeds.
1.2. Proposed Research
The power system is carefully designed and operated so
that most transmission line outages do not propagate over
the system and it only has to encompass one or few out-
ages occurring together. This paper deals exactly with
those situations where failure may propagate, protections,
controls and other factors may not operate as desired, and
several components of the system may be affected. As
previous references, failure propagation is modeled using
probabilistic models, allowing for multiples failures
modes.
Power grids differ one from another mainly in topol-
ogy, size, capacity, interconnectedness, loading level,
and several other physical/technical features. The plan-
ning and operation of the market or the power system
also varies, but not as widely as physical features (dis-
patch rules, unit co mmitments, market clearing processes
differs but have similar goals and results).
Although these differences exist, outage data seems to
suggest similar cascading failure behavior in widely dif-
ferent systems. As such, research is still undergoing
aiming to identify the best probabilistic models for cas-
cading modeling in power systems. In this paper, we
compare the fitness of 4 different statistical models to th e
14-year utility outage data from a regional power grid.
This paper is organized as follows. In section II, out-
age data sources and handling procedures to group fail-
ures are presented. In section III three probabilistic mod-
els ever used for transmission line outage analysis are
introduced first. Utility outage data is introduced in sec-
tion III, and also the simple grouping techniques of util-
ity outage d ata for bra n ching pr oc ess based anal ysis.
2. Utility Outage Data
Cascading failure models are very constrained by outage
data availability and some models require some pre-
possessing or handling the data. This section address
these topics, describing different data sources, the data
set used here and the handling procedures required to fit
the models.
2.1. Main Sources of Utility Outage Data
For the researches on cascading large blackouts, the util-
ity outage data are valuable references on modeling and
useful diagnostics in monitoring the process and extent
of blackouts. Since data is scarce, here we summarize the
data available from cited references.
Ref. [4] summarized the results of a survey of design
characteristics of and outage experience with overhead
transmission at voltage 230kV and above in USA and
Canada, for a purpose of providing technical support on
the probabilistic system models for planning and opera-
tion. The outage data were sub mitted by utilities from all
nine NERC/USA reliability regions and by the Canadian
Electric Association representing all of Canada. The sta-
tistics provided classifications and analysis on 38,489
outage data according to voltage level, region, causes, or
duration time, etc.
Every year, the North American Electrical Reliability
Council (NERC) publishes a documented list summariz-
ing major disturbances [7], which is used as strong evi-
dence in abovementioned researches for bigger probabil-
ity of large blackouts.

H. REN ET AL.
916
Ref. [8] provides a historical outaged data recorded by
a North American utility over a period of 12.4 years and
is being upgraded constantly. The transmission line out-
age data is required by NERC for the Transmission
Availability Data System (TADS). The data for each
transmission line outage includes the outage time (to the
nearest minute) as well as other data. All the line outages
are automatic trips. More than 99% of the outages are of
lines rated 69kV or above and 97 % of the outages are of
lines rated 115kV or above. There are several types of
line outages in the data and a variety of reasons for the
outages [6] .
Our previous research and the work of this paper are
based on 9-year historical outage data in [1] and 14-year
outage data in this paper, which are extracted from the
fault data information recorded by protective relays in a
regional power grid. The data we can reach provides the
voltage level and the time stamp of the failure, the se-
quence of the failures, and failure cause, however with
on specific information on load shed. The data set is de-
scribed in details in next section.
2.2. Utility Outage Data Used in this Paper
The outage data used in this paper is from a regional
electric power transmission system with, approximately,
190 220kV buses, and 12 buses at 500kV. The data is
recorded over about 14 years staring in 1997 and ending
in 2011.
The historical outage data is extracted from the report
containing the outage details recorded by fault recorder
devices and the fault analysis by relay engineers. The
extracted information includes the contingency type
(transmission line failure, or busbar failure, or generator
failure…), contingency time (to the nearest minute), vol-
tage level, and the auto-recloser’s action. In this research,
only transmission line outages in 220kV and 500kV are
computed in the model. Outages at lower voltage levels
are not considered because of the potential number of
unrecorded events.
When processing the outage data, the voltage level,
line outage type (single phase or three-phase and detailed
causes of the line outages are neglected, and are regarded
as the same. The neglecting in the bulk statistical analy-
sis is appropriate, for no matter what the details on caus-
es, type or voltage levels are, and they all result in the
weakness of the transmission system to various extent.
The more sever the outage is (outages on higher voltage
level, or more initial outages, or poor operation and con-
trol techniques), the more sever outcomes follows, such
as even more outages, while bulk statistical analysis
based on the historical outage data actually takes all of
these into consideration, and lead to a more credible
evaluation on system’s risk level.
Large flashover events in the data with approximately
260 outages over two days are neglected because of
lacking time tags. There is not large cascading blackout
(totally blackout) in this regional power grid over the
analyzed horizon. Data recording is not perfect and there
is some kind of incomplete outage data recording, those
should be smaller failures, not big ones. Therefore the
tail part in the probability distribution (PDF) versus out-
ages with various sizes should be credible.
The clustering of outages in stages can be seen in
Figure 1. The x-axis shows time since start of cascade
for outages in each of the 458 cascades. The first min of
each cascade is shown. Multiple outages at the same time
are shown slightly displaced.
2.3. Data Grouping by Stages
The processing in this section for the outage data is
mainly for the application of branching process model.
Here, we follow the data grouping technique in [1]. The
outage data are grouped according to their time stamps
without considering the geographical information of the
outage. Although successive outages in areas far way
from each other may not have direct electrical connec-
tions, but the successive happening does suggest a further
weakening of the system. Moreover, when the data is in
bulk and the system is in large-scale, the difficulty from
considering more detail information of each outage
would compromise the application of the method.
Successive outages separated in time by more than one
hour are assumed belong to different cascades, for op-
erator actions are usually completed within one hour.
Successive outages in a given cascade separated in time
by more than one minute are assumed in different stages
within that cascade, for transients or auto-recloser actions
are completed within one minute.
733 outages are abstracted from the failure records,
and from them, 459 cascades are obtained by the intro-
duced grouping technique. Table 1 is obtained by sum-
ming over all the 459 cascades the number of outages in
Figure 1. Clustering of outages in stages.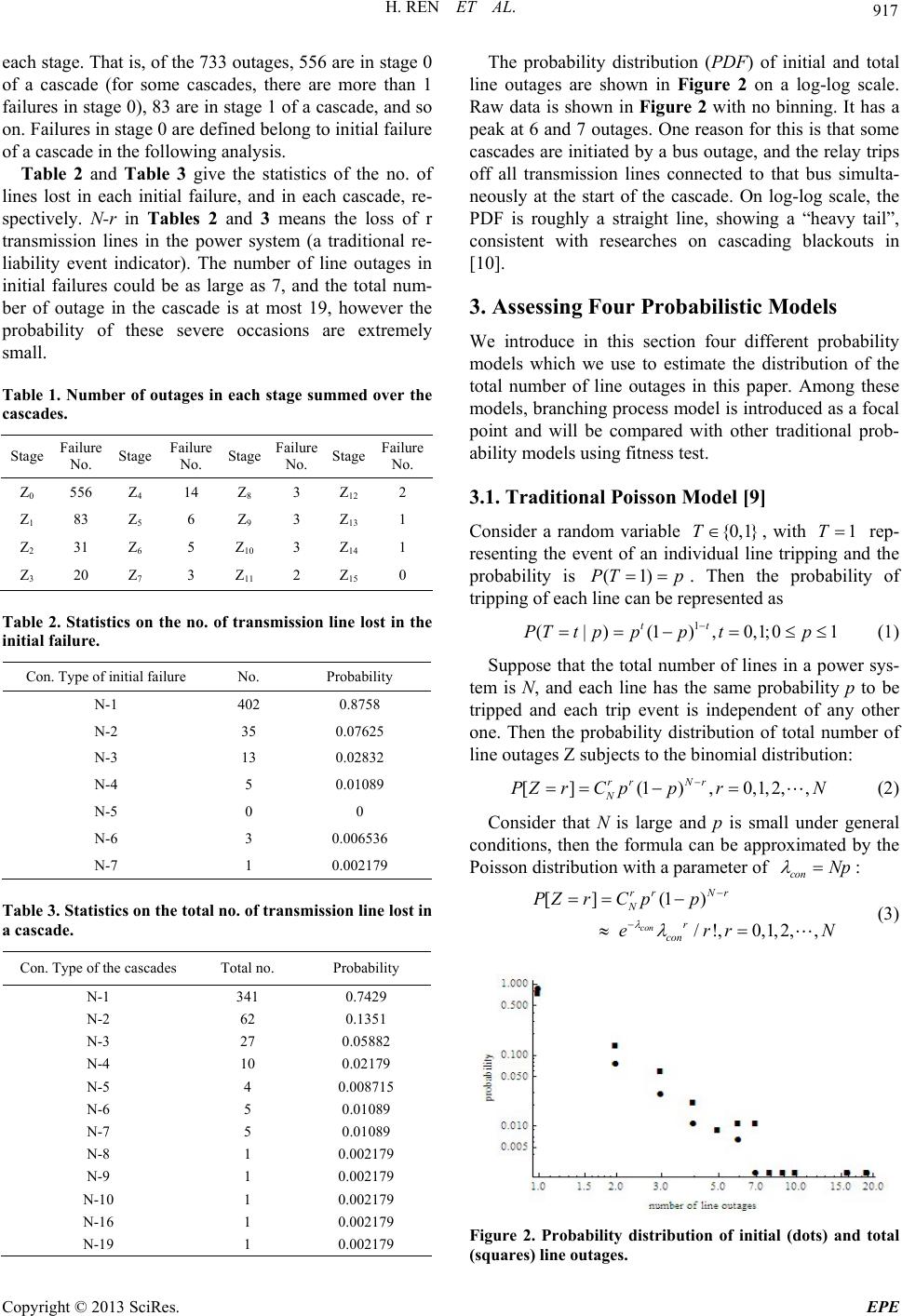

H. REN ET AL. 917
each stage. That is, of the 733 outages, 556 are in stage 0
of a cascade (for some cascades, there are more than 1
failures in stage 0), 83 are in stage 1 of a cascade, and so
on. Failures in stage 0 are defined belong to initial failure
of a cascade in the following analysis.
Table 2 and Table 3 give the statistics of the no. of
lines lost in each initial failure, and in each cascade, re-
spectively. N-r in Tables 2 and 3 means the loss of r
transmission lines in the power system (a traditional re-
liability event indicator). The number of line outages in
initial failures could be as large as 7, and the total num-
ber of outage in the cascade is at most 19, however the
probability of these severe occasions are extremely
small.
Table 1. Number of outages in each stage summed over the
cascades.
Stage Failure
No. Stage Failure No. Stage Failure No. Stage Failure No.
Z0 556 Z4 14 Z8 3 Z12 2
Z1 83 Z5 6 Z9 3 Z13 1
Z2 31 Z6 5 Z10 3 Z14 1
Z3 20 Z7 3 Z11 2 Z15 0
Table 2. Statistics on the no. of transmission line lost in the
initial failure.
Con. Type of initial failure No. Probability
N-1 402 0.8758
N-2 35 0.07625
N-3 13 0.02832
N-4 5 0.01089
N-5 0 0
N-6 3 0.006536
N-7 1 0.002179
Table 3. Statistics on the total no. of transmission line lost in
a cascade.
Con. Type of the cascades Total no. Probability
N-1 341 0.7429
N-2 62 0.1351
N-3 27 0.05882
N-4 10 0.02179
N-5 4 0.008715
N-6 5 0.01089
N-7 5 0.01089
N-8 1 0.002179
N-9 1 0.002179
N-10 1 0.002179
N-16 1 0.002179
N-19 1 0.002179
The probability distribution (PDF) of initial and total
line outages are shown in Figure 2 on a log-log scale.
Raw data is shown in Figure 2 with no binning. It has a
peak at 6 and 7 outages. One reason for this is that some
cascades are initiated by a bus outage, and the relay trips
off all transmission lines connected to that bus simulta-
neously at the start of the cascade. On log-log scale, the
PDF is roughly a straight line, showing a “heavy tail”,
consistent with researches on cascading blackouts in
[10].
3. Assessing Four Probabilistic Models
We introduce in this section four different probability
models which we use to estimate the distribution of the
total number of line outages in this paper. Among these
models, branching process model is introduced as a focal
point and will be compared with other traditional prob-
ability models using fitness test.
3.1. Traditional Poisson Model [9]
Consider a random variable , with {0 ,1}T1T

rep-
resenting the event of an individual line tripping and the
probability is (1)PT p

. Then the probability of
tripping of each line can be represented as
1
(|)(1),0,1;0
tt
PTt ppptp
1

  (1)
Suppose that the total number of lines in a power sys-
tem is N, and each line has the same probability p to be
tripped and each trip event is independent of any other
one. Then the probability distribution of total number of
line outages Z subjects to the binomial distrib ution:
[](1),0,1,2, ,
rr Nr
N
PZrC pprN

  (2)
Consider that N is large and p is small under general
conditions, then the formula can be approximated by the
Poisson distribution with a parameter of con Np


:
[] (1)
/!,0,1,2,,
con
rr Nr
N
r
con
PZrC pp
err




 
 N
(3)
Figure 2. Probability distribution of initial (dots) and total
(squares) line outages.

H. REN ET AL.
918
In this paper, we use maximum likelihood estimation
[15] to estimate the parameter con

. If the space X is
discrete with probability distributiunction
()(;)PX xpx
on f

 ,
then the joint probability distributionction of event fun
1122
{,,, }
nn
X
xX xXx  can be shown as
n
11
()(,,;)( ;)
n
i
LLxxpx
i





 (4)
where

ter is the model parameter to be estimated. The parame value

 which makes (4) reach the maxi-
mum value is called as maximum likelihood estimator,
we can find out

 by mathematical methods such as
derivation.
We can get based on Table 2 and
m
(5)
3.2. Power Law Model [10-11]
a normalized dis-
6)
When we draw the relationship of
on
power law
(7)
3.3. Branching Process Model [1]
0.5970
con
 
ood estimatio

aximum likelihn. The estimated distribu-
tion is as follows:


0.5970 1
[]0.5970/ (1)!,1,2,
r
PZ rerr
The total number of lin e outages Z has
tribution as shown in (6) when it follows a power law:
[|]/ ,0;1,2,
qq
PZr qrrqr

 
 (
[]PZ r
t line wi
and r
a log-log plot, we will find a straighth slop
/q qr

, this indicates the distribution follows a
. Using maximum likelihood estimation intro-
e
duced above, we can get 2.0q
 based on Table 2,
then the expression of using poaw model to estimate
the distribution of outage lines can be shown as follows:

 
wer l
2.0 2.02.0
1
[] /0.645,1,2,
k
PZ rrrrr

 

The propagation

which means the mean number of
child failures for each parent failure plays a critical role
in branching process. We consider

as an invariant
constant in this paper, the positive nuber of failures in
stage zero 0
m
Z
will produce outages in the next stage
with a meanmber of 0 nu
Z

, the child failures then be-
come parents to produce ges with a mean number of
20
outa
Z
 in the next stage and so on [12]. Here we use the
d introduced in [1] to estimate metho

:
() ()()
12 ()
1
() ()()
01 ()1
1
(
()
)
Ni
i
Jii i
Ni
i
ZZ Z
ZZ Z











(8)
where
Jii i
represents the total number of line outages,
p ()Ni reresents the maximum stage with nonzero fail-
Based on Table 1 and (8), we can know ures.
J
12 14
01 13
0.24
ZZ Z

ZZ Z


 (9)
1. Generalized Poisson model numbers follows a 3.2.
If the distribution of initial failure
Poisson distribution with the parameter

and ignores
the condition with zero initial failure, theistribution of
initial numbers is as follows: d
0
[] ,1,2,
(1) !
r
e



PZ r r
er
 
 
 (10)
e mean number of initial failures can be sh own Th
0/(1 )
Z
e




 (11)
n get We ca01.211Z base
ator d on Table 2, and then we get the estim.3965 using (11). The distri-
bution of the total num outages under this con-
dition follows generalized Poisson distribution [13] as
shown in (12).
ˆ0
 
ber of line
1
0.24 0.3965
1
0.3965
[]( )
(1) !
0.3965(0.240.3965),
(1) !
3.2.2. B
1,2
r
r
r
r
e
PZ rrer
e
rer
r









 



(12)
orel-Tanner model ollows arbitrary distribution, If the initial failure numbers f
then the total number of line outages follows a Borel-
Tanner distributi on [14].

0
0
0
0
1
10000
0.24
1
1000 0
0
() ()
0.24(0.24 )()!
1, 2,;1, 2,
r
rz
r
z
r
rz
r
z
e
!
rPZz zrrz
e
PZzzrrz
rzr








  
 


 

(13)
PZ

where 00 PZ z




Table 2. can be calculated based on the data
4. Comparison Analysis of 4 Probabilistic
he expressions in (5), (7), (12), and (13) for
given in
Models
evaluate tWe
the loss of different number of lines, i.e.


1,2,3,4,5,. .. ,10r.
Probabilities obtained from 4 models and recorded out-
age data are listed in Table 4, where G-P represents Ge-
neralized Poisson, and B-T represents Borel-Tanner. The

H. REN ET AL. 919
probabilities in Table 4 are given in Figrue 3. Figrue 3
shows Log-Log plots of PDFs in Poission model in (5)
(Inverse triangles), Power Law model in (7) (triangles),
Generalized Poisson branching process in (12) (squares),
Borel-Tanner branching process in (13) (diamonds) and
observed data (dots).
For outages fewer than 5, all models fit well (as shown
in
view, the probability dis-
tri
able 4. Probabilities from 4 Probabilistic Models and Ob-
Branching process
Figure 3). However, Borel-Tanner branching process
model is better than the other 3 models for outages big-
ger than losing 5 lines. Power law overestimates the
probability of larg er outages. The curve generated by the
Poisson model deviates heavily from the observed data,
underestimating the probability of large events (r>5) by
roughly a factor of 10-2 to 10-5.
In order to get a more clear
bution of total number of outages from observed data
and estimated using Borel-Tanner branching process are
given in Figure 4. We can see that the distribution esti-
mated using Borel-Tanner branching process can fit the
distribution from data well, and in the log- log plot it also
shows a heavy tail.
T
served Data.
r No. o
f
Observed Poisson Power
failure data law G-P B-T
1 341 0.7429 0.5505 0.6450 0.0.63986877
2 62 0.1351 0.3286 0.1613 0.2211 0.1776
3 27 0.05882 0.09809 0.07167 0.082760.06875
4 10 0.02179 0.01952 0.04031 0.032730.03128
5 4 0.008715 0.002913 0.02580 0.013470.01419
6 5 0.01089 0.00034790.01792 0.0057070.007945
7 5 0.01089 0.000034610.01316 0.0024740.005052
8 1 0.002179 2.952E-060.01008 0.0010920.003183
9 1 0.002179 2.203E-070.007963 .00048900.001912
10 1 0.002179 1.461E-080.006450 .00022170.001098
Figure 4. PDFs of total No. of outages from observed data
Chi-square test is then used to provide a quantitative
co
(dots) and by Borel-Tanner branching process (line).
mparison among 4 models, and the test result is given
in Table V. The Chi-square test [21] is widely used in
statistics to test the fitness of a probability model to sa m-
ple data. Suppose
X
follows the discrete distribution
with the possible values of 1, 2,,k, and the probability
can be shown as ()PX ik,1
i
p i

. If we perform
n trials, and the event
X
i

results (1,2,,)
i
X
ik
es, then we can use tatistic timth2 e s

to show how
much the samples deviate from the ribution to be
tested: dist
2
2
1
()
kii
ii
X
np
np



 (14)
when n, 2

follows the chi-square distribution
2

wfom number 1k. We can obtain
(14) that the larger the statis2
ith the reed
fromtic

, the larger the
deviation. Since the condition to let conclusion in-
troduced above be true is that the distribution must be a
polynomial distribution and all of the i
np should be
larger than 5, we decompose the sample space into 5 ex-
clusive sets
the
12 3
45
{1}, {2}, {3},
{4},{5,6, }.
MM M
MM
 


s
The test result is shown in Table 5. If there are es-
timated parameters in the probability model, the freedom
number of the 2

distribution should be changed to
1ks

. For insce, for the Borel-Tanner model, tan

meter to be estimated, so the freedom number
chi-square distribution is 5-1-1=3; but for the generalized
Poisson model, the parameters that should be estimated
are
is a paraof

and

, so the freedom number is changed to be
5-2-2. By ispecting Table 4, the value of 2 1= n

calcu-
lated from the Borel-Tanner model is obvioussmaller
than the values gotten from other models, that illustrates
the Borel-Tanner model is far more fit than the other
ly
Figure 3. Log-Log plots of PDFs of 4 probabilistic models.

H. REN ET AL.
920
st Results For all models.
B-T aw Poisson
Table 5. χ2 Te
G-P Power L
r Xi pi npi p
i npi ppi p i npi i n
1 341 0.7 30.8 2 0.0 2 0.5 2 68715.7 63993.764596.155052.7
2 62 0.1776 81.5 0.2211 101.5 0.1613 74.04 0.3286 150.8
3 27 0.06875 31.56 0.08276 37.99 0.07167 32.90 0.09809 45.02
4 10 0.03128 14.36 0.03273 15.02 0.04031 18.50 0.01952 8.960
>=
r-13 2 3 3
9. 3 2 2
519 0.03467 15.91 0.02361 10.84 0.08172 37.51 0.00329 1.510
m-
χ2 314.072.8792.4
odels. When we set the significance level be 0.01, m
the 2

of the Borel-Tanner model satisfies
22
(3) 11.34  ,
0.01
that illustrates the Borel- Tanner model can exactly de-
5. Conclusions
ilistic models, Poisson model, Power
scribe the distribution of real data under a significance
level of 0.01.
We apply 4 probab
Law model, Generalized Poisson Branching process
model and Borel-Tanner Branching process model, to a
14-year historical outage data from a regional power grid
in China, computing probabilities of cascading line out-
ages. We group the line outages into cascades and stages
according to their outage times. For this data, the em-
pirical distribution of the total number of line outages is
well approximated by the initial line outages propagating

according to a Borel-Tanner branching process with
opagation parameter. For this data, Power law model
overestimates the probability of larger outages, while the
probability distribution generated by the Poisson model
deviates heavily from the observed data, underestimating
the probability of large events (outage no. greater than 5)
by roughly a factor of 10-2 to 10-5. The observation is
confirmed by a statistical test of model fitness. The re-
sults of this work justify further testing of Borel-Tanner
branching process models, leading to a promising re-
search avenue for cascading failure modeling.
pr
6. Acknowledgements
ted from National Science
REFERENCES
[1] H. Ren and I. ission Line Outage
Data to Estimate Cascading Failure Propagation in an
Electric Power System,” IEEE Transactions on Circuits
and Systems, Vol. 55, No. 9, 2008, pp. 927-931.
doi:10.1109/TCSII.2008.924365
[2] IEEE PES CAMS Task Force on understanding, pred
tion, mitigation and restoration ofic- cascading failures, Ini-
s for Cascading Failure Analysis in Transmission
anadian Over-
tial review of methods for cascading failure analysis in
electric power transmission systems,” IEEE Power Engi-
neering Soc. General Meeting, Pittsburgh PA USA, Jun.
2008.
[3] D. Watts and H. Ren, “Classification and Discussion on
Method
System,” ICSET, Singapore, Nov. 2008.
[4] R. Adler, S. Daniel, C. Heising, M. Lauby, R. Ludorf and
T. White, “An IEEE Survey of US and C
head Transmission Outages at 230 kV and above,” IEEE
Transactions on Power Delivery, Vol. 9, No. 1, 1994, pp.
21 -39.doi:10.1109/61.277677
[5] Q. Chen, C. Jiang, W. Qiu and J. D. McCalley, “Probabil-
ity Models for Estimating the Probabilities of Cascading
Outages in High-voltage Transmission Network,” IEEE
Transactions on Power Systems, Vol. 21, No.3, August
2006, pp.1423-1431. doi:10.1109/TPWRS.2006.879249
[6] I. Dobson, “Estimating the Propagation and Extent of
Cascading Line Outages from Utility Data with a Branch-
ing Process,” IEEE Transactions on Power Systems, Vol.
27, No.4, 2012, pp. 2146-2155.
doi:10.1109/TPWRS.2012.2190112
[7] Information on Electric System D
America can be Downloaded from th
isturbances in North
e NERC Website at
for Self-organized Criticality in Electric
http://www.nerc.com/dawg/database.html.
[8] Bonneville Power Administration Transmission Services
Operations & Reliability w e b s i te
http://transmission.bpa.gov/Business/Operations/Outages.
[9] Q. Chen and J. D. McCalley, “A Cluster Distribution as a
Model for Estimating High-order Event Probabilities in
Hui Ren thanks the suppor
Research Foundation of China (51107040), and thanks
engineers from the regional power grid for the providing
of the historical outage data for research. David Watts
thanks the supported from Fondecyt project 1110527.
Power Systems,” 8th International Conference on Prob-
abilistic Methods Applied to Power Systems. Ames, Iowa,
2004, 622-628.
[10] B. A. Carreras, D. E. Newman, I. Dobson and A. Poole,
“Initial Evidence
Power System Blackouts,” Proceedings of the 33rd An-
nual Hawaii International Conference on System Sci-
ences, 2000, pp. 1411-1416.
Dobson, “Using Transm

H. REN ET AL. 921
doi:10.1109/HICSS.2000.926768
[11] I. Dobson, J. Chen, J. Thorp, B. A. Carreras and D.
lackouts in Power
E.
Newman, “Examining Criticality of B
System Models with Cascading Events,” Proceedings of
the 35th Annual Hawaii International Conference on
System Sciences, 2002, pp. 803-812.
doi:10.1109/HICSS.2002.993975
[12] I. Dobson, B. A. Carreras and D. E. Ne
ing Process Approximation to Cascading
wman, “A B
Load-dependen
as, V. E. Lynch
. Lynch and D.
ics for Engineers &
ranch-
t Scientists, Seventh Edition. Pearson Education Asia Lim-
ited and Tsinghua University Press.
System Failure,” The 37th HICSS. 2004.
[13] I. Dobson, K. R. Wierzbicki, B. A. Carrer
and D. E. Newman, “An Estimator of Propagation of Cas-
cading Failure,” the 39th HICSS．2006．
[14] I. Dobson, K. Wierzbicki, B. A. Carreras, V
E. Newman, “An Estimator of Propagation of Cascading
Failure,” The 39th HICSS, 2006.
[15] R. E. Walpole, Probability & Statist