Energy and Power Engineering, 2013, 5, 850-856
doi:10.4236/epe.2013.54B163 Published Online July 2013 (http://www.scirp.org/journal/epe)
Analysis and Modeling of Buck Converter in
Discontinuous-Output-Inductor-Current
Mode Operation*
Jianbo Yang1, Weiping Zhang2，Faris Al-Naemi1，Xiaoping Chen2,
1Materials and Engineering Research Institute (MERI), Sheffield Hallam University (SHU), Sheffield, UK
2Lab of Green Power & Energy System (GPES), North China University of Technology (NCUT), Beijing, China
Received September, 2012
ABSTRACT
The Buck converter with LC input filter operating in discontinuous output current mode has a high power factor with a
constant duty cycle. A Buck converter in this operation mode can reduce the reverse recovery loss of the freewheeling
diode thus increase the efficiency. The operation, power factor analysis and modeling of the converter are studied in this
paper. Experimental results are presented to verify the theoretical predictions.
Keywords: Buck Converter; Power Factor Correction; Modeling
1. Introduction
AC/DC converter has been studied as a high-power-fac-
tor rectifier. The most popular power stage circuit of the
AC/DC converter is a Boost converter [1,2]. The Boost
converter has an input inductor which naturally makes
the input current continuous and less of harmonics.
However, the disadvantage is the output has to be higher
than the peak input voltage. Unlike the Boost AC/DC
converters, the Buck AC/DC converters have step-down
characteristics as the output voltage is lower than the
peak input voltage. The buck converter with LC input
filter operating in discontinuous output inductor current
mode has resistive and constant input impedance with a
constant duty cycle D and a constant switching cycle Ts.
Thus, the average input current of the converter follows
the input voltage with a constant duty ratio control.
The low-frequency behavior modeling of the Buck
converter with LC input filter operating in discontinuous
output inductor mode is presented in this paper. Based on
the model, the characteristic of the converter and the
conditions for power factor correction is studied. The
experimental verification is also given.
2. Power Stage
2.1. Circuit Configuration
The buck converter with LC input filter is shown in Fig-
ure 1. The discontinuous output inductor current mode
means the current through the inductor L2 is zero during
part of one switching cycle. The converter can still oper-
ate in discontinuous capacitor voltage mode which means
the voltage across C1 is zero during part of a switching
cycle. These two operation modes can be considered as
dual of each other [3]. However, the voltage stress of the
switch and diode will be very high when the converter
operates in discontinuous capacitor voltage mode [4].
2.2. Operation Principles
The operation principles of the converter and the charac-
teristic waveforms are presented in Figure 2.
There are three phases for the Buck converter with LC
input filter operating in discontinuous inductor current
mode.
Phase 1: 0~DTs. switch S is turned on. D is reverse-
biased. When the operation is in steady state, the average
voltage across L1, over one switching cycle, is zero. The
average voltage across C1 over one switching cycle is
*Project supported by Natural Science foundation of China (N0.
51277004). The Importation and Development of High-Caliber Talents
Project of Beijing Municipal Institutions (No.IDHT20130501) Figure 1. Buck AC/DC converter with LC input filter.

J. B. YANG ET AL. 851
(a) 0~DTs
(b) DTs~DpTs
(c) DpTs~Ts
(d) Swiching waveforms
Figure 2. Discontinuous inductor current operation and
waveforms.
equal to the input voltage. C1 operates in continuous
mode that 1c is small during one switching cycle.
Thus, the average voltage across C1 over one switching
cycle can be considered as the instantaneous voltage
across C1. Therefore, L2 is charging under constant volt-
age (V). The peak current through L2 is:
u
o
V
i

2
2
()
io
p
s
VV
I
DT
L

 (1)
The current through C1 is 2i
I
I. When 2i
I
I

, 1
c
is positive, C1 is charging. When
i
2i
I
I, C1 is dis-
charging.
Phase 2: DTs~DpTs. S is closed D is forward-biased.
L2 is discharging and the current through L2 falls to zero
at DpTs. C1 is charging. The peak current through L2 can
also be obtained as:

2
2
o
p
p
V
s
I
DDT
L
 (2)
Phase 3: DpTs~Ts; the switch S is still turned off.
Current through L2 falls to zero. Output is supported by
C2 individually. Combination of (1) and (2), the follow-
ing equation can be obtained.
i
o
p
V
VDD
D

 (3)
If the switching period Ts is much smaller than the
input cycle Ti, the input voltage can be considered con-
stant over one switching cycle [3]. Then, the input volt-
age i in (1), (3) can be directly replaced by
during half of line cycle .
Vsin
ii
Vwt
i
T
2
2
(sin )
iio
p
s
VwtV
I
DT
L

 (4)
sn i
ii
o
p
Vwt
VDD
D

(5)
io
VV can be defined as η. then from equation (5), the
relation between η and D is
sin i wt
D

 (6)
Therefore, the converter will operate in discontinuous
inductor current mode throughout half line cycle
when
i
T
1D

.
3. Power Analysis
As shown in Figure 2, the input current i
I
is the sum of
the switch current
s
i and current through C11c. The
average current through C1 is zero during one switching
cycle in the steady state. Thus, the average input current
equals to the average switching current over one switch-
ing cycle. According to (2) and (4), the average input
current, over one switching cycle, can be obtained as,
i
2
2
(sin )
2
io
iavg s
VwtV
I
DT
L

 (7)
where iavg means the average input current over one
switching cycle. As the switching cycle
I
s
T is much
smaller than the input cycle i, the input current can be
considered constant over one switching cycle. Buck
T

J. B. YANG ET AL.
852
converter operates only when the input voltage is higher
than the output voltage. Therefore, (7) is valid only when
o
. When the input rectified voltage equals to
the output voltage,
sin i VwtV
1
11
arcsin arcsin
o
iii
V
twVw

 (8)
α is defined as the ratio between the output voltage and
the peak of the rectified input voltage. Thus, over half
input line cycle, operation is possible only for
11
(, )
2
i
T
tt t ,
as shown in Figure 3. The average input power with
constant duty ratio and constant switching cycle
s
T is
provided in (9). As referred to (5), the maximum duty
cycle D is η for maintaining the converter operate in dis-
continuous inductor current mode. Substitution of D for
η in (9), the following relation can be obtained in (10).
1
1
2,
2 22
2
2
=
Tsin
21 2
(1 arcsin)
4
i
Tt
iiiiavg
t
i
is
PVwtIdt
VDT
L









(9)
2 22
2
21 2
(1 arcsin)
4
is
i
PVT
L

 


 (10)
The relation between active input power and conver-
sion ratio η with maximum duty ratio is plotted in Figure
4. As shown, with D = η, the converter operates in the
boundary of the discontinuous inductor current mode and
the maximum active input power will be obtained when η
is near 0.58.
The root mean square value of the input current can be
obtained from (7) as
2
2
2
2 2
2
2
(sin )
2
2
61 2
=(12)(1arcsin)
22
ii
i
Ttio
irms s
t
i
is
VwtV
IDTdt
TL
VDT
L







 

(11)
the power factor is obtained from (10) and (11) as,
2
2
2
21 2
1arcsin
.
61 2
(12)(1arcsin )
i
irms irms
P
PF VI











 

(12)
where P.F is the power factor. It is clear that the power
factor is affected only by conversion ratio η when the
duty cycle D is constant. The relation is plotted in Figure
5.
t
t
Figure 3. Operation waveforms during half input cycle.
00.1 0.20.3 0.4 0.50.6 0.70.8 0.91
0.4
0.5
0.6
0.7
0.8
0.9
1


power factor & conversi on rat i o
Figure 4. Active Input Power vs Conversion Ratio η (from
equation (10)).
00.1 0.2 0.30.4 0.50.60.7 0.80.91
0
100
200
300
400
500
600
700

ac tiv e input power p

& active input power
Figure 5. Power Factor vs Conversion Ratio η (from equa-
tion (12)).
It is shown that the power factor is reversely propor-
tional to the conversion ratio η.
When 0.6


the power factor will be higher than
0.9. The results are exact the same as [5]. When η is very
small, . Then the input current will be sin
oi
VVi wt
2
2
sin
2
ii
iavg s
Vwt
I
DT
L
 (13)

J. B. YANG ET AL.
853
The equivalent input impendence is resistive,
(21)
2
2
2
i
s
L
RDT
 (14)
The power factor turns out to be unity. Therefore, with
constant duty cycle D and constant switching cycle Ts,
the lower output voltage, the higher power factor. where,
4. Modeling
The low-frequency model is obtained by considering the
relative voltage or current will not change over one
switching cycle since the switching cycle is much higher
than the input line frequency. Therefore, the average
value, over one switching cycle, is considered as an in-
stant value during one switching cycle [4,6]. By assum-
ing that the voltage across C1 is continuous and constant
over a switching cycle, the average switch current
s
i
and average current through L2 over one switching cycle
can be obtained from Figure 2.
2
1
2
2
s
s
V
I
DDT
L
 (15)
2
21
2
()
21
s
V
I
DDDT
L
 (16) () ()
oi
VsVs is output-input transfer function and
() ()
o
VsDs is the output-control transfer function. The
transfer function between output voltage and duty cycle
given by (21) has three poles and two zeros. This can be
approximate to have a single pole which is exactly the
same as the traditional Boost converters [6,7].
As the average voltage across L2 is zero over one
switching cycle.
12
1
2
VV
D
V

D (17)
5. Results
As shown in Figure 1, the following equations can be
obtained. 5.1. Simulations
11
1
1
()(() ()) ()*
si 1
I
sVsVsVss
sL
C (18) Simulations were carried out to verify the discontinuous
inductor current operation of the circuit. The components
used are: L1 = 500u. L2 = 20u, C1 = 220n. C2 = 2000u, D
= 0.1, R = 13. The input voltage is 220VAC and the out-
put voltage is 36 V. The results are illustrated as follows
(Figures 6 - 9), which show that input current will follow
the input voltage automatically when Buck converter
with an input LC filter operates in discontinuous inductor
current with a constant the duty ratio.
222
1
() ()()
Is VssCR  (19)
2
() ()
o
Vs Vs

(20)
Derivation and Laplace transform of (15) ~ (17) and
substitution of the results into (18) ~ (19), the following
can be obtained.
0.12 0.140.16 0.180.20.22
Time
(
s
)
0
-2
-4
2
4
VP17/100I9*2
Figure 6. Input voltage and input current (220Vac; 0.52A).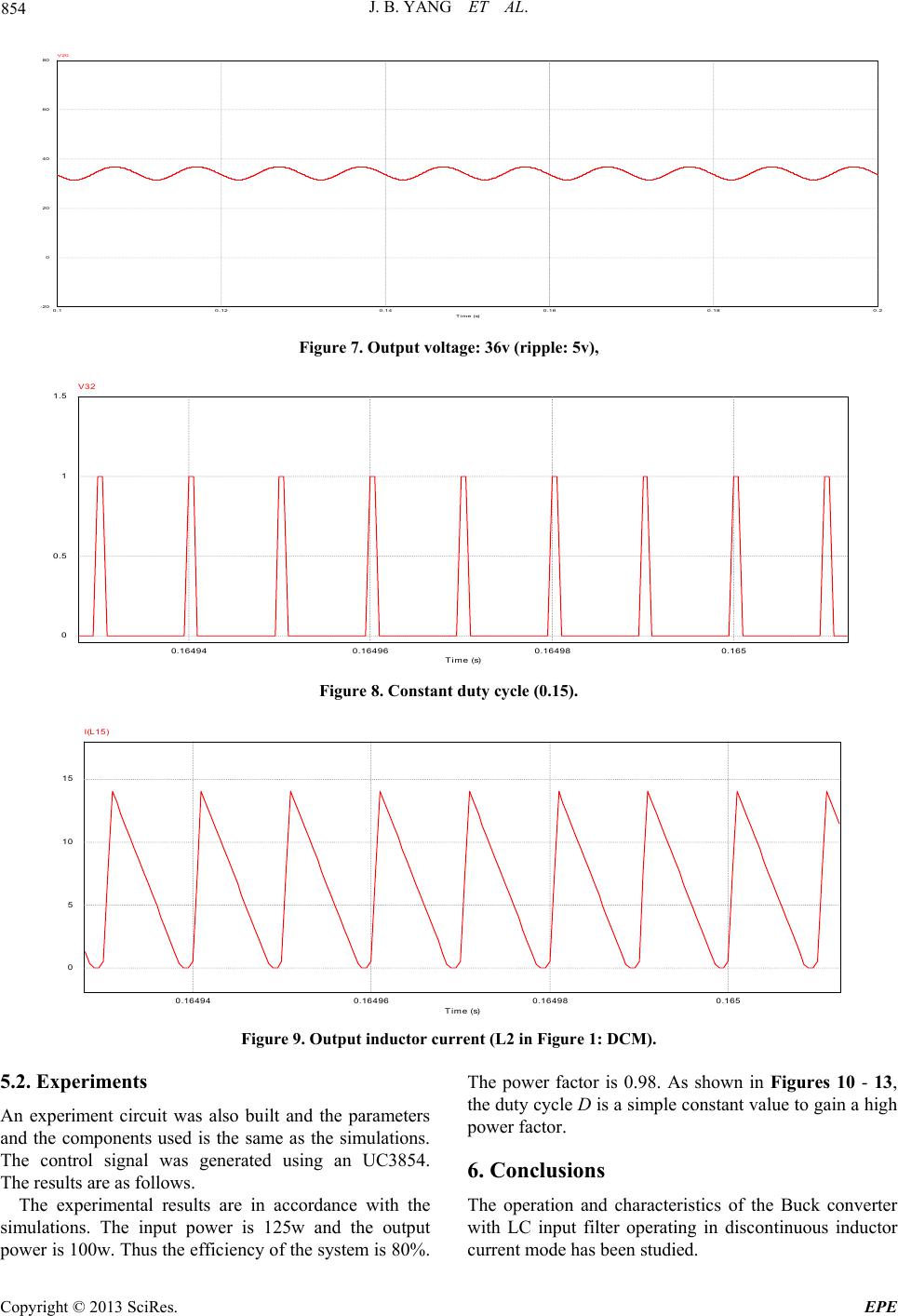

J. B. YANG ET AL.
854
0.10.12 0.14 0.16 0.180.2
Time (s)
0
-20
20
40
60
80 V20
Figure 7. Output voltage: 36v (ripple: 5v),
0.16494 0.164960.164980.165
Time (s)
0
0.5
1
1.5 V32
Figure 8. Constant duty cycle (0.15).
0.16494 0.164960.164980.165
Time (s)
0
5
10
15
I(L15)
Figure 9. Output inductor current (L2 in Figure 1: DCM).
5.2. Experiments
An experiment circuit was also built and the parameters
and the components used is the same as the simulations.
The control signal was generated using an UC3854.
The results are as follows.
The experimental results are in accordance with the
simulations. The input power is 125w and the output
power is 100w. Thus the efficiency of the system is 80%.
The power factor is 0.98. As shown in Figures 10 - 13,
the duty cycle D is a simple constant value to gain a high
power factor.
6. Conclusions
The operation and characteristics of the Buck converter
with LC input filter operating in discontinuous inductor
current mode has been studied.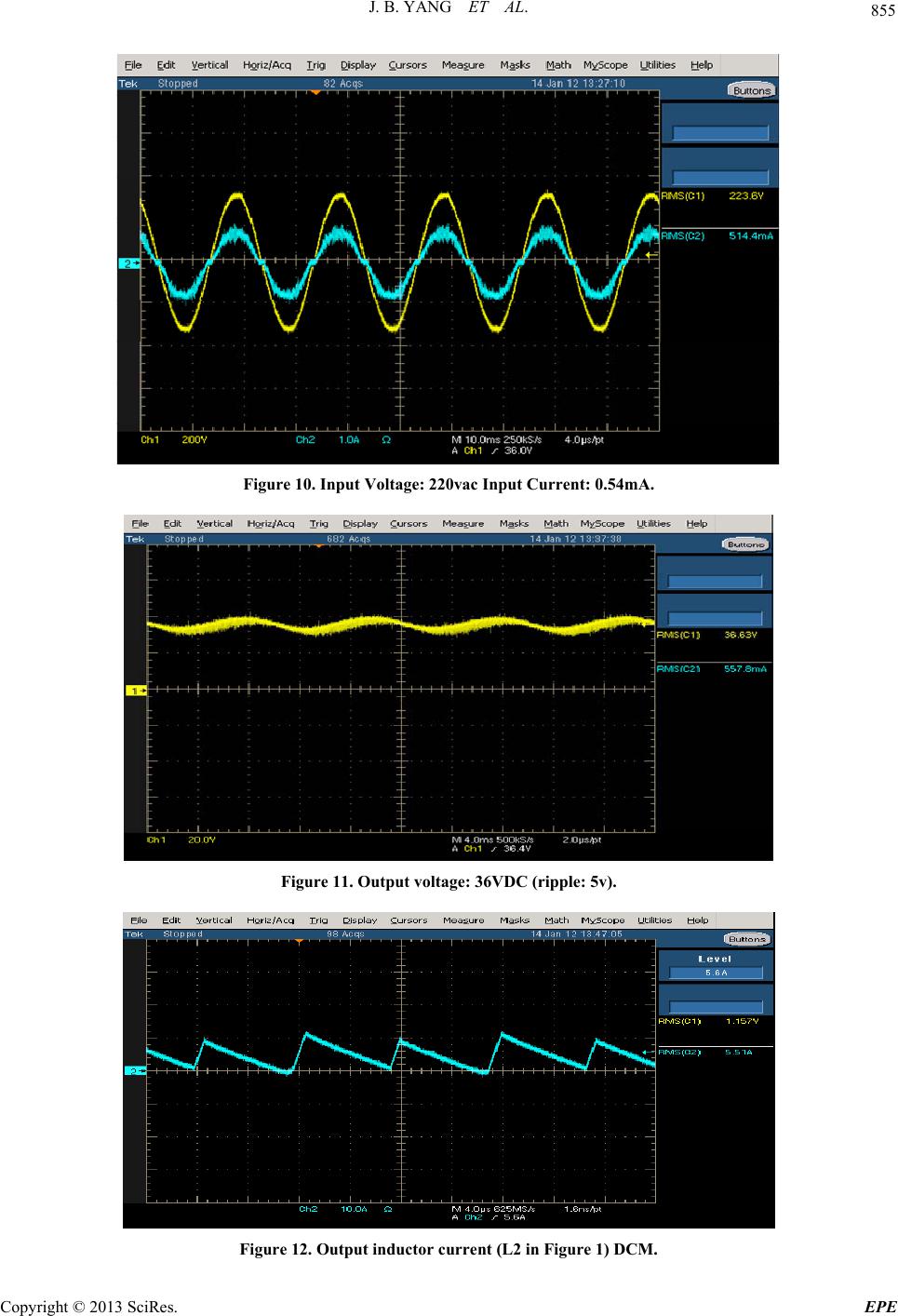

J. B. YANG ET AL. 855
Figure 10. Input Voltage: 220vac Input Current: 0.54mA.
Figure 11. Output voltage: 36VDC (ripple: 5v).
Figure 12. Output inductor current (L2 in Figure 1) DCM.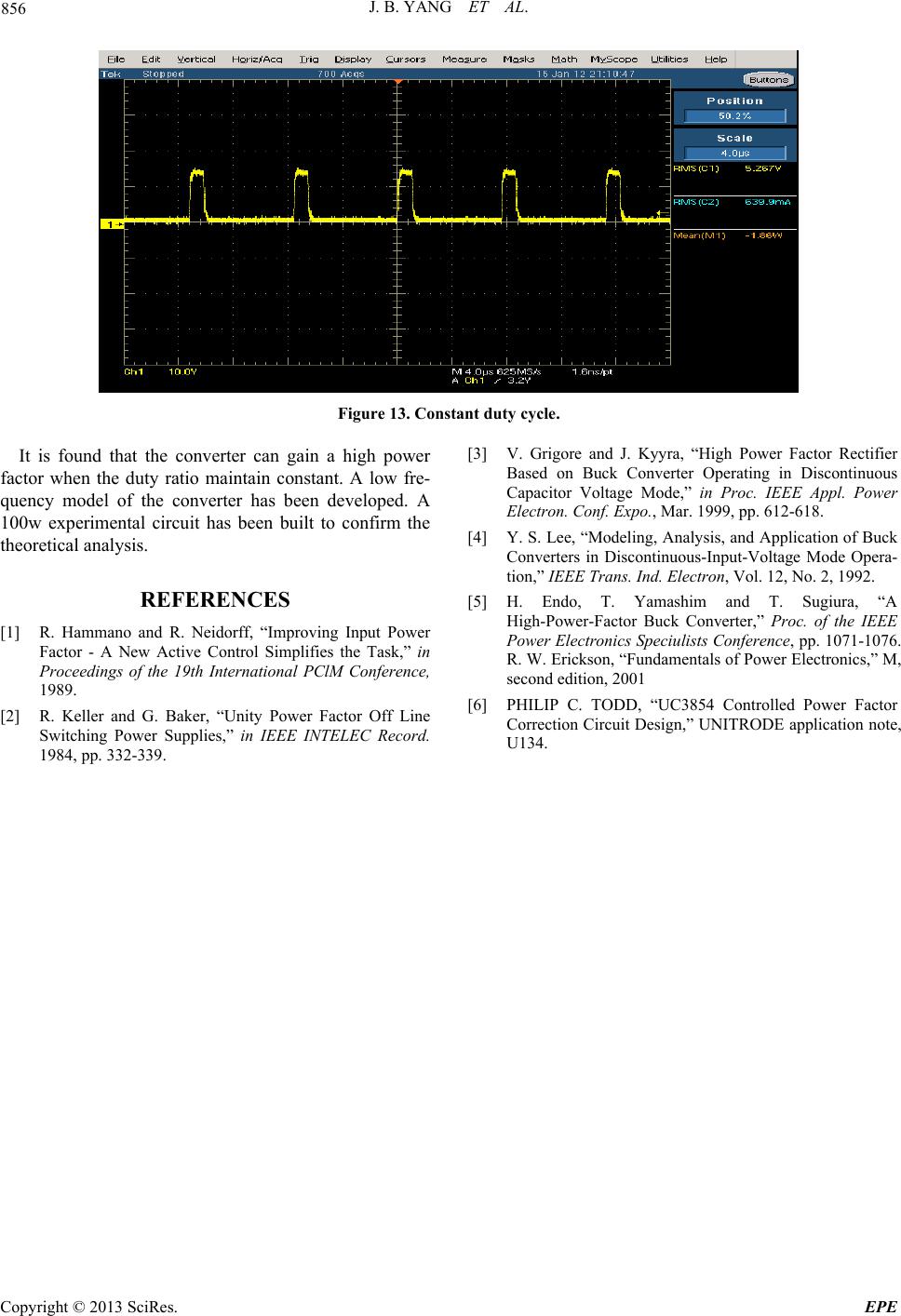

J. B. YANG ET AL.
856
Figure 13. Constant duty cycle.
It is found that the converter can gain a high power
factor when the duty ratio maintain constant. A low fre-
quency model of the converter has been developed. A
100w experimental circuit has been built to confirm the
theoretical analysis.
REFERENCES
[1] R. Hammano and R. Neidorff, “Improving Input Power
Factor - A New Active Control Simplifies the Task,” in
Proceedings of the 19th International PClM Conference,
1989.
[2] R. Keller and G. Baker, “Unity Power Factor Off Line
Switching Power Supplies,” in IEEE INTELEC Record.
1984, pp. 332-339.
[3] V. Grigore and J. Kyyra, “High Power Factor Rectifier
Based on Buck Converter Operating in Discontinuous
Capacitor Voltage Mode,” in Proc. IEEE Appl. Power
Electron. Conf. Expo., Mar. 1999, pp. 612-618.
[4] Y. S. Lee, “Modeling, Analysis, and Application of Buck
Converters in Discontinuous-Input-Voltage Mode Opera-
tion,” IEEE Trans. Ind. Electron, Vol. 12, No. 2, 1992.
[5] H. Endo, T. Yamashim and T. Sugiura, “A
High-Power-Factor Buck Converter,” Proc. of the IEEE
Power Electronics Speciulists Conference, pp. 1071-1076.
R. W. Erickson, “Fundamentals of Power Electronics,” M,
second edition, 2001
[6] PHILIP C. TODD, “UC3854 Controlled Power Factor
Correction Circuit Design,” UNITRODE application note,
U134.