Energy and Power Engineering, 2013, 5, 842-849
doi:10.4236/epe.2013.54B162 Published Online July 2013 (http://www.scirp.org/journal/epe)
A High Power Factor Rectifier Based on Buck Converter
Operating in Discontinuous Inductor Current Mode*
Jianbo Yang1, Weiping Zhang2，Faris Al-Naemi1，Xiaoping Chen2
1Materials and Engineering Research Institute (MERI), Sheffield Hallam University (SHU), Sheffield, UK
2Lab of Green Power & Energy System (GPES), North China University of Technology (NCUT), Beijing, China
Received September, 2012
ABSTRACT
By adding a suitable LC filter to the input of a Buck converter, a high-power-factor buck converter is proposed. The
converter can operate in the discontinuous-output-current mode operation. A Buck converter in this operation mode
features simple control as the constant duty cycle PWM used. The operation condition of the converter is studied. The
validity of analysis is verified by Simulation and Experimental results.
Keywords: Discontinuous-output-current; Buck Converter; Power Factor Correction
1. Introduction
Intensive research has been carried out to improve the
power factor of AC/DC converters [1]-[4]. Among the
research, it has been reported that by adding a suitable
LC filter to the input of a Buck converter to make the
converter operate as power factor correction circuit [5]
[6]. An example of the converter is presented in Fig. 1.
The input capacitor C1 usually has a low enough value
and the voltage across it can be discontinuous. Then a
high-power-factor can be obtained by a simple constant
duty ratio PWM control. However, the voltage stress
across switch(S in Figure 1) and diode (D in Figure 1)
imposes major restrictions as the peak value of Vc1 is
very high when Vc1 becomes zero for part of the switch-
ing cycle. In this paper, the Buck converter with LC in-
put filter operates in a “discontinuous-output-current”
mode. The current of output inductor (L2 in Figure 1)
fells to zero for part of the switching cycle and the volt-
age of the input capacitor (C1) becomes continuous. Thus,
the peak value of Vc1 is reduced substantially and switch
voltage stress will be no longer a restriction. Besides the
reverse recovery loss of the freewheeling diode (D) is
reduced.
The goal of this paper is to give a more comprehensive
analysis of Buck converter with the LC input filter oper-
ating in DICM. In section 2 of this paper, the principle of
DICM is analyzed. Based on the analysis, the character-
istics of the converter and the conditions for power factor
correction are studied in section 3. In section 4, the sim-
ulation and experimental verifications are given.
2. Operation Principles of DICM
2.1. Operation with Constant Input
As shown in Figure 1, if C1 has large enough value, it
will operate in CCVM and the voltage across C1can be
considered constant during one switching cycle. L1 has
large value so that the input current i
I
can be consid-
ered as constant. Inductor L2 has low enough value and
operates in DICM. With these assumptions, the converter
is the same as the Buck DC/DC converter operating in
DCM and the characteristic waveform are presented in
Figure 2. The operation over one switch cycle is as fol-
lows:
1) 0 < t < DTs: at t = 0, S is turned on. The current
through C1 is io
I
I

. L2 is charging under constant
voltage (io
VV

).The current through L2 increases line-
arly from zero. Accordingly, the current through C1 de-
creases linearly. When 2i
I
I
2i
, 1c is positive, C1 is
charging. And when
i
I
I is turned to negative,
C1 is discharging.
1c
i
*Project supported by Natural Science foundation of China (N0.
51277004). The Importation and Development of High-Caliber Talents
Project of Beijing Municipal Institutions (No.IDHT20130501) Figure 1. Buck AC/DC converter with LC input filter.

J. B. YANG ET AL. 843
Figure 2. Waveforms for buck converter in DICM.
2) DTs < t < DpTs: at t = DTs, S is turned off. D starts
to conduct. L2 is discharging under output voltage. The
current through L2 decreases to zero. C1 is charging with
input current.
3) DpTs < t < Ts: the current through L2 maintains ze-
ro. The output is supported by C2. C1 is still charging by
the input current.
The average voltage across inductor L1, over one
switch cycle, is zero in stationary state. Therefore, the
average voltage across capacitor C1 is equal to the input
voltage. As C1 is large enough the changes of voltage
across it during a switch cycle can be disregarded. Thus,
the instantaneous voltage across C1 can be considered the
same as the average voltage across it. As a result, the
voltage across C1 is the input voltage.
Based on the analysis above, the maximum current
through L2 is,
2
2
()
io s
P
VVDT
IL

 (1)
The average current through capacitor C1, over one
switching cycle, is zero in steady state. The input current
equals to the average switch current
s
I
over one switch
cycle.
2
2
p
i
I
I
D (2)
Substitution of (1) into (2) gives
2
2
()
2
io s
i
VVDT
IL

 (3)
The conversion ratio can be defined as o
i
V
kV 
Then an equivalent input resistance i as the ratio
between input voltage and input current is obtained,
R
2
2
2
(1 )
i
s
L
RkDT  (4)
The equivalent input resistance i is proportional to
L2 and inversely proportional to switching cycle Ts and
duty ratio D.
R
2.2. Operation with Sinusoid Input
The input voltage of the off-line Buck AC/DC converter
is a rectified sinusoid voltage.
() sin
ip
vt Vwti
(5)
where 2
ii
wT


and is the input cycle.
i
T
The switching cycle
s
T is usually much smaller than
the input cycle i. Thus, the input voltage can be con-
sidered constant over one switching cycle. Thus, the
analysis of the converter with rectified sinusoid input
over one switching cycle is the same as the converter
with constant input. Simply substitution of (5) into (3),
the input current is then
T
2
2
(sin )
() 2
p
io
i
VwtVDT
it L

s (6)
If sin
p
i
VwtVo , the input current can be simplified
as,
2
2
sin
() 2
p
i
i
VwtDT
it L
s
(7)
Thus, the input current is proportional to the input
voltage when the duty ratio is constant.
Buck converter operates only when the input voltage is
higher than the output voltage. Therefore, (6) is valid
only for sin
ii
tVo Vw When the input rectified volt-
age equals to the output voltage,
1
11
arcsin arcsin
o
iii
V
twVw

 (8)
o
p
V
V
 . Thus, over half input line cycle, operation is
possible only for1 (, )
2
i
T
tt t
1

 as shown in Figure 3. As
t
t
Figure 3. Operation waveforms during half input cycle.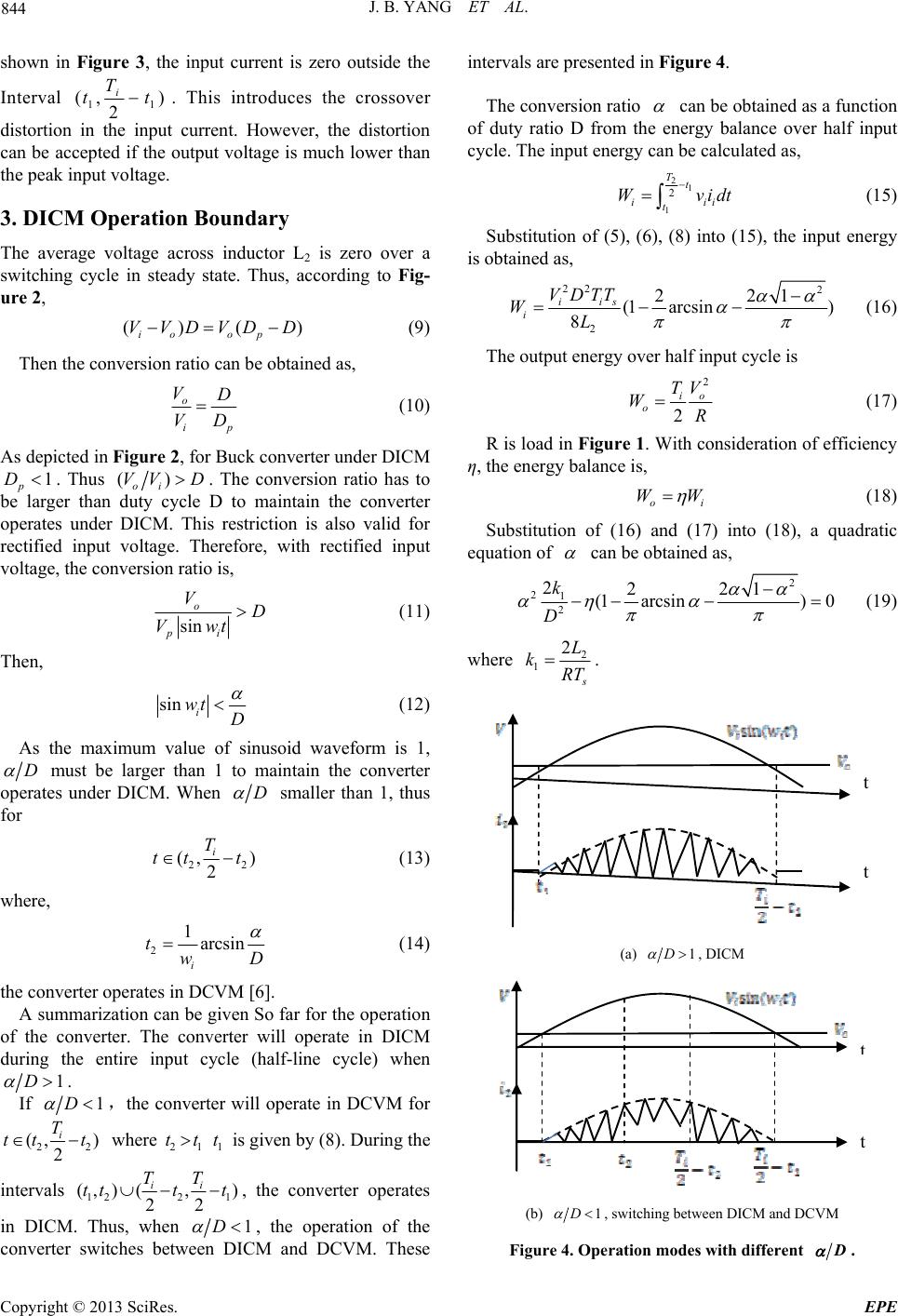

J. B. YANG ET AL.
844
shown in Figure 3, the input current is zero outside the
Interval 1 (, )
2
i
T
tt1
)
. This introduces the crossover
distortion in the input current. However, the distortion
can be accepted if the output voltage is much lower than
the peak input voltage.
3. DICM Operation Boundary
The average voltage across inductor L2 is zero over a
switching cycle in steady state. Thus, according to Fig-
ure 2,
() (
io op
VVDVDD  (9)
Then the conversion ratio can be obtained as,
o
ip
VD
VD
 (10)
As depicted in Figure 2, for Buck converter under DICM
. Thus
1
p
D()
oi
VV D. The conversion ratio has to
be larger than duty cycle D to maintain the converter
operates under DICM. This restriction is also valid for
rectified input voltage. Therefore, with rectified input
voltage, the conversion ratio is,
sin
o
pi
VD
Vwt
 (11)
Then,
sin i wt D

 (12)
As the maximum value of sinusoid waveform is 1,
D

must be larger than 1 to maintain the converter
operates under DICM. When D

smaller than 1, thus
for
2
(, )
2
i
T
tt t
2
(13)
where,
2
1arcsin
i
twD

 (14)
the converter operates in DCVM [6].
A summarization can be given So far for the operation
of the converter. The converter will operate in DICM
during the entire input cycle (half-line cycle) when
1D

.
If 1D

，the converter will operate in DCVM for
22 21
tt1 t (, )
2
i
T
tt t where is given by (8). During the
intervals 12 (,tte converter operates
in DICM. Thus, when
2
,
22
ii
TT
t 1 ) () , t th
1D


, the operation of the
converter switches betweenM and DCVM. These
intervals are presented in Figure 4.

DIC
The conversion ratio can be obtained as a function
of duty ratio D from the energy balance over half input
cycle. The input energy can be calculated as,
21
Tt

1
2
ii
i
t
Wvidt (15)
Substitution of (5), (6), (8) into (15), the input energy
is obtained as,
2
VD
22
2
221
(1 arcsin)
8
iis
i
TT
WL





 (16)
The output energy over half input cycle is
2
TV
2
io
o
WR  (17)
R is load in Figure 1. With consideration of efficiency
η, the energy balance is,
oi
WW


(18)
Substitution of (16) and (1
eq
7) into (18), a quadratic
uation of

can be obtained as,
2
21
2
2221
(1arcsin) 0
k
D

 



  (19)
where 2
1
2
s
L
kRT .
t
t
1D  , DICM (a)
t
t
(b) 1D 

, switching between DICM and DCVM
Figure 4. Operation modes with different
D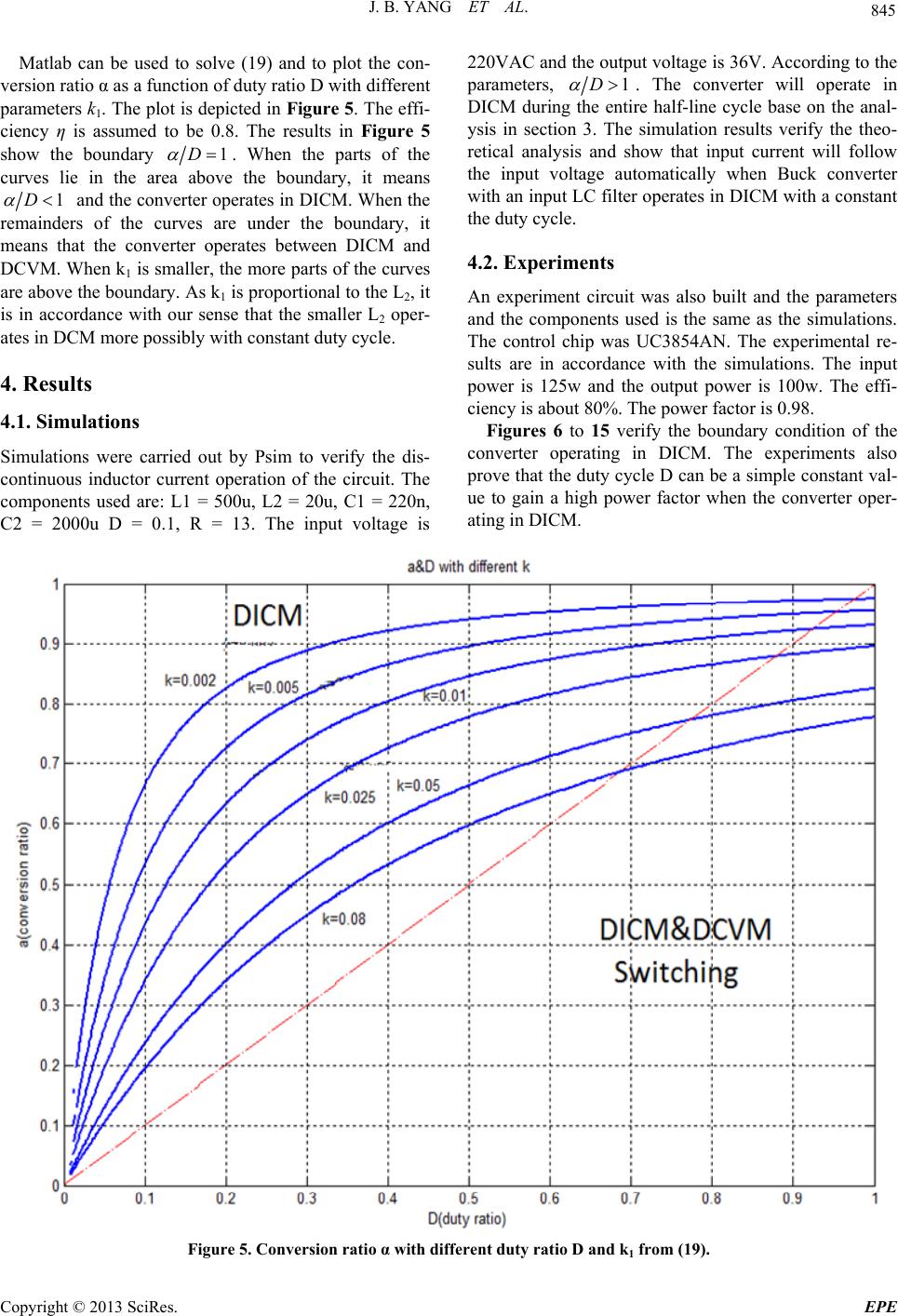
 .

J. B. YANG ET AL.
845
Maot thcon-
ve
220VAC and the output voltage is 36V. According to the
parameters, 1D

. The converter will operate in
DICM during the entire half-line cycle base on the anal-
ysis in section 3. The simulation results verify the theo-
retical analysis and show that input current will follow
the input voltage automatically when Buck converter
with an input LC filter operates in DICM with a constant
the duty cycle.
tlab can be used to solve (19) and to ple
rsion ratio α as a function of duty ratio D with different
parameters k1. The plot is depicted in Figure 5. The effi-
ciency η is assumed to be 0.8. The results in Figure 5
show the boundary 1D

. When the parts of the
curves lie in the are the boundary, it means a above
1D

 and the converter operates in DICM. When the
ers of the curves are under the boundary, it
means that the converter operates between DICM and
DCVM. When k1 is smaller, the more parts of the curves
are above the boundary. As k1 is proportional to the L2, it
is in accordance with our sense that the smaller L2 oper-
ates in DCM more possibly with constant duty cycle.
remaind
4. Results
ions
rried out by Psim to verify the dis-
4.2. Experiments
An experiment circuit was also built and the parameters
and the components used is the same as the simulations.
The control chip was UC3854AN. The experimental re-
sults are in accordance with the simulations. The input
power is 125w and the output power is 100w. The effi-
ciency is about 80%. The power factor is 0.98.
4.1. SimulatFigures 6 to 15 verify the boundary condition of the
converter operating in DICM. The experiments also
prove that the duty cycle D can be a simple constant val-
ue to gain a high power factor when the converter oper-
ating in DICM.
Simulations were ca
continuous inductor current operation of the circuit. The
components used are: L1 = 500u, L2 = 20u, C1 = 220n,
C2 = 2000u D = 0.1, R = 13. The input voltage is
Figure 5. Conversion ratio α with different duty ratio D and k1 from (19).

J. B. YANG ET AL.
846
0.15 0.160.17 0.18 0.190.2
Time (s)
0
-2
-4
2
4I9 VP17/150
Figure 6. Input voltage and input current (220Vac; 0.52A).
0.15 0.160.17 0.18 0.190.2
Time (s)
0
-2 0
20
40
60
80 V20
Figure 7. Output voltage: 36v (ripple: 5v).
0.16442 0.16443 0.16444 0.16445 0.16446 0.164470.16448
Time (s)
0
0.5
1
1.5
V34
Figure 8. Constant duty cycle (0.15).

J. B. YANG ET AL. 847
0.16442 0.16443 0.16444 0.16445 0.16446 0.164470.16448
Time (s)
0
5
10
15
I(L15)
Figure 9. Output inductor current (L2 in Figure 1: DCM).
0.150.160.170.18
Time (s)
0
50
100
150
200
250
300
350
VP18
Figure 10. Input capacitor voltage (C1 in Figure 1: CCM).
Figure 11. Input Voltage: 220vac Input Current: 0.54mA).

J. B. YANG ET AL.
848
Figure 12. Output voltage: 36VDC (ripple: 5v).
Figure 13. Output inductor current (L2 in Figure 1) DCM.
Figure 14. Input capacitor voltage (C1 in Figure 1) CCM.

J. B. YANG ET AL.
849
Figure 15. Constant duty cycle (0.15).
5. Conclusions
The Buck converter with LC input filter operating in
DICM can gain a high power factor when the duty ratio
maintain constant. Composed to the BOOST PFC con-
verter, the Buck PFC converter can obtain an output
voltage lower than the peak of the input voltage, which is
suitable for the low DC voltage application. The detailed
analysis presented in the paper suggested that the Buck
converter may switch between DICM and DVCM if
. When 2
1
2
s
L
kRT  1D

is constant, the duty ratio is
proportional to the conversatio
voltage is constant, thus, the duty ratio is actually re-
versely proportional to the input voltage.
A 100 w prototype has been built and the results veri-
fied the theoretical analysis in this paper
REFERENCES
[1] D. S. Chen and J.-S. Lai, “A Study of Power Correction
Boost Converteroperating at CCM-DCM Mode,” in Proc.
IEEE Southeastcon, Vol. 93, pp. 6-13.
[2] W. Tang, Y. Jiang, G. C. Hua, F. C. Lee and I. Cohen,
“Power Factor Correction with Flyback Converter Em-
ploying Charge Control in APEC ’93 Rec., pp. 293-298
[3] V. Vlatkovic, D. Borojevic and F. C. Lee, “Input Filter
Design for Power Factor Correction Circuits,” in IE-
CON ’93 Rec., Vol. 2, pp. 954-958.
[4] E. X. Yang, Y. Jiang, G. C. Hua and F. C. Lee, “Isolated
Boost Circuit for Power Factor Correction,” in IEEE
APEC ’93 Rec., pp. 196-203.
[5] Y. S. Lee, “Modeling, Analysis, and Application of Buck
uous-Input-Voltage Mode Opera-
nd. Electron., Vol. 12, No. 2,
MARCH 1997.
[6] V. Grigore and J. Kyyra, “High Power Factor Rectifier
Based on Buck Converter Operating in Discontinuous
Capacitor Voltage Mode,” in Proc. IEEE Appl. Power
Electron. Conf. Expo., Mar. 1999, pp. 612-618.
Nomenclature
DICM Discontinuous Inductor Current Mode
DCVM Discontinuous Capacitor Voltage Mode
CCVM Continuous Capacitor Voltage Mode
CICM Continuous Inductor Voltage Mode [6]
n ratio α. As the output Converters in Discontin
tion,” IEEE Trans. I