Communications and Network, 2013, 5, 271-275
http://dx.doi.org/10.4236/cn.2013.53B2050 Published Online September 2013 (http://www.scirp.org/journal/cn)
An MDP Based Energy Efficient Transmission Policy for
W ir eless Terminals
Xiao-Hui Lin, Yi-De Huang, Chao Yang, Ning Xie, Bin Chen, Shengli Zhang, Hui Wang
Faculty of Information Engineering, ShenZhen University, China
Received July, 2013
ABSTRACT
In wireless network, terminals are usually energy constrained. In order to extend the lifetime of the terminal, the limited
energy must be utilized in an efficient manner. In this paper, under the constant transmission power scenario, we pro-
pose an Energy Efficient Transmission Policy (EETP) which is derived by using Markov Decision Process (MDP). The
simulation results show that compared with the Threshold Transmission Policy (TTP), the proposed policy can reduce
the energy consumption significantly, while satisfying the performance demand at the same time.
Keywords: Energy Efficient; Transmission Policy; MDP; Tradeoff
1. Introduction
Wireless communication systems have deeply penetrated
into our daily life and the wireless terminals such as
smart phone, tablet PC and wireless sensor node have
brought fundamental changes to our society. However,
the design of wireless system is a challenging task, in
which, many issues must be properly handled. Among
these design issues, one of the most crucial one is en-
ergy-efficiency of wireless system.
In literature, there have been a lot of research works on
the design of energy-efficient communication systems.
The design philosophy is usually to achieve the required
level of performance by consuming just enough en-
ergy.Specifically, in [1], Uysal-Biyikoglu formulates the
problem as how to minimize the energy consumption
while satisfying the delay constraints at the same time. In
order to reduce the energy consumption, In [2] based on
the queue length in the system, Curt Schurgers proposed
a traffic adaptive technique called Dynamic Modulation
Scaling (DMS) which adaptively change the modulation
level to lower the overall energy consumption, while
bounding the packet delay at an acceptable level. In[3],
Baris Ata studies how to control the transmitting power
based on the buffer state. The objective is to minimize
long-run average energy consumption subject to a QoS
constraint, which is expressed as an upper bound on the
packet loss rate. Author also formulates the issue into a
Lagrangian problem and derives the optimal power con-
trol policy.
In [4], Liu analyzes the cross-layer design of AMC
system. Specifically, both the queue length and channel
state have been considered. By deriving the stationary
probability of the system state, Liu gives a performance
analysis model and develops a cross-layer design method.
The work is novel, but the author doesn’t consider the
energy issue. In this paper, we adopt the Liu’s method in
the performance analysis and try to design an energy
efficient transmission system.
2. System Model
2.1. Markov Model for Wireless Channels and
AMC
In this paper, we focus on the uplink transmission. Ter-
minals transmit data to base station through wireless
channel. We assume the channel is a block fading chan-
nel. It means that the channel is frequency flat, and re-
mains invariant per frame, but is allowed to vary from
frame to frame, which is suitable for slowing varying
wireless channel. And we adopt Finite State Markov
Channel (FSMC) model to describe the channel. FSMC
is a popular model adopted in literature [4-6]. Specifi-
cally, the channel quality can be captured by the received
signal-to-noise ratio (SNR). By partitioning the range of
the received SNR into a finite number of intervals, a fi-
nite-state model for the fading channel is built [7]. We
use to denote the different state
of the channel, and let A0 < A1 <A2 …< AN+1 be the
thresholds of different state. If the instantaneous received
SNR is between Ak and Ak+1, we will say the channel is
in state Sk. Based on the method in [4-7], we can get the
channel state transition probability matrix Pc.
{} ,0 ,1, ...
n
Sn N
C
opyright © 2013 SciRes. CN

X.-H. LIN ET AL.
272
In our study, we adopt the adaptive physical layer de-
sign called ABICM [8], in which variable throughput
modulator and channel coding are used. We assume a
4-mode AMC configuration is used. Therefore, there are
four distinctive throughputs available as listed in Ta ble 1.
We divide the channel into five different states {S0; S1;
S2; S3; S4} according to the instantaneous channel quality.
Note that when channel is in state S0, no packet is sent
because the channel is in deep fading. So if the feedback
CSI falls within the interval {Ak;Ak+1} k = 0,1,2,3,4,
transmission mode k is selected.
The processing unit at the data link layer is packet that
includes multiple information bits. And each packet at
this layer is assumed to contain a fixed number of bits
(NP). At physical layer, the information delivery is per-
formed in a frame-by-frame manner. And in physical
layer, the symbol rate (RS) and the frame duration are
assumed to be constant, which means that each frame
contains a fixed number of symbols (Ns).
Therefore, based on the modulation and coding rate
pair adopted in Table 1, we can find that the number of
packets one frame can carry is1:2:4:8. Since the transmit
power is constant, the energy needed to transmit one
packet under different modes is 8:4:2:1. So we should
transmit in higher mode as much as possible to conserve
energy.
2.2. Buffer Queuing Analysis
In [4], authors originally propose a discrete time queuing
analysis method which is also used in the performance
analysis in our paper, with some emendations made to fit
the situations in our work. The queuing model is illus-
trated in Figure 1.
Table 1. AMC system.
Mode1 Mode2 Mode3 Mode4
Modulation QPSKK 8PSK 32QAM 512QAM
Coding rate 1
2
2
3
4
5
8
9
bits/symbol 1 2 4 8
ThresholdAk 5.016 10.035 13.826 17.381
Figure 1. Queuing model.
Let t denote the time units and At the number of pack-
ets arriving at time t. The time unit in our study is frame
duration Tf . For simplicity, let the arrival process be
At= a for all t (1)
Let Bt denote the buffer state which is the number of
packets currently stored in the buffer. Thus we have
Bt
∈ B B = {0 , 1 , 2 , 3 · · · K} (2)
We use Ct to denote the channel state at time t, which
can be written as
Ct
∈ C C = {S
0
, S
1
, S
2
,· · · S
N
} (3)
In our study, we use buffer state Bt and channel state
Ct to form a state pair (Ct, Bt). The number of packet that
one time unit can transmit is highly related with the sys-
tem state (Ct, Bt). We use Gt to denote the action (i.e.
number of packets to transmit) we can select at time t,
thus we have
Gt
∈ G G = {0 , 1 , · · · min(C
t ,
B
t
)} (4)
At any time t, based on the Bt, Ct, Gt and At, we can
get Bt+1 by
B
t+1
= B
t
−G
t
+A
t
(5)
Then we can get the queue state transition probability
as
1
1&
(|(,),)
0
tjit
tttt
if GGBBAG
Pb BCBG
ot her wise







t
(6)
Gt can be decided by the transmission policy g, which
indicates how many packets we should transmit under
the current system state. When we have the system state
(Ct, Bt), guided by the transmission policy g, we can get
the transmission decision Gt = g(Ct, Bt). Then the buffer
transition probability (6) can be calculated.
In order to understand the system better, we need to
derive the system state transition probability and station-
ary distribution. Since the channel process and queue
process are independent with each other, based on Pc and
(6) we can get the system state transition probability
P ((Ct+1, Bt+1)|(Ct, Bt), Gt)
= P
C(Ct+1|Ct)  PB(Bt+1|Bt, g(Ct, Bt)) (7)
Based on the method proposed in [4] (24-26), we can
derive the stationary distribution Pg(c, b), (c, b) ∈ C ×
B under the transmission policy g.
Then we can calculate the desired performance under
different transmission policy and find the optimal one.
The packet loss rate Pd is [4] (27-30):
E[D] = ∑ max[0,a − K + (b − g(c, b))] * Pg(c,b) (8)
;
[]
dd
cCbB
ED
PP
a


(9)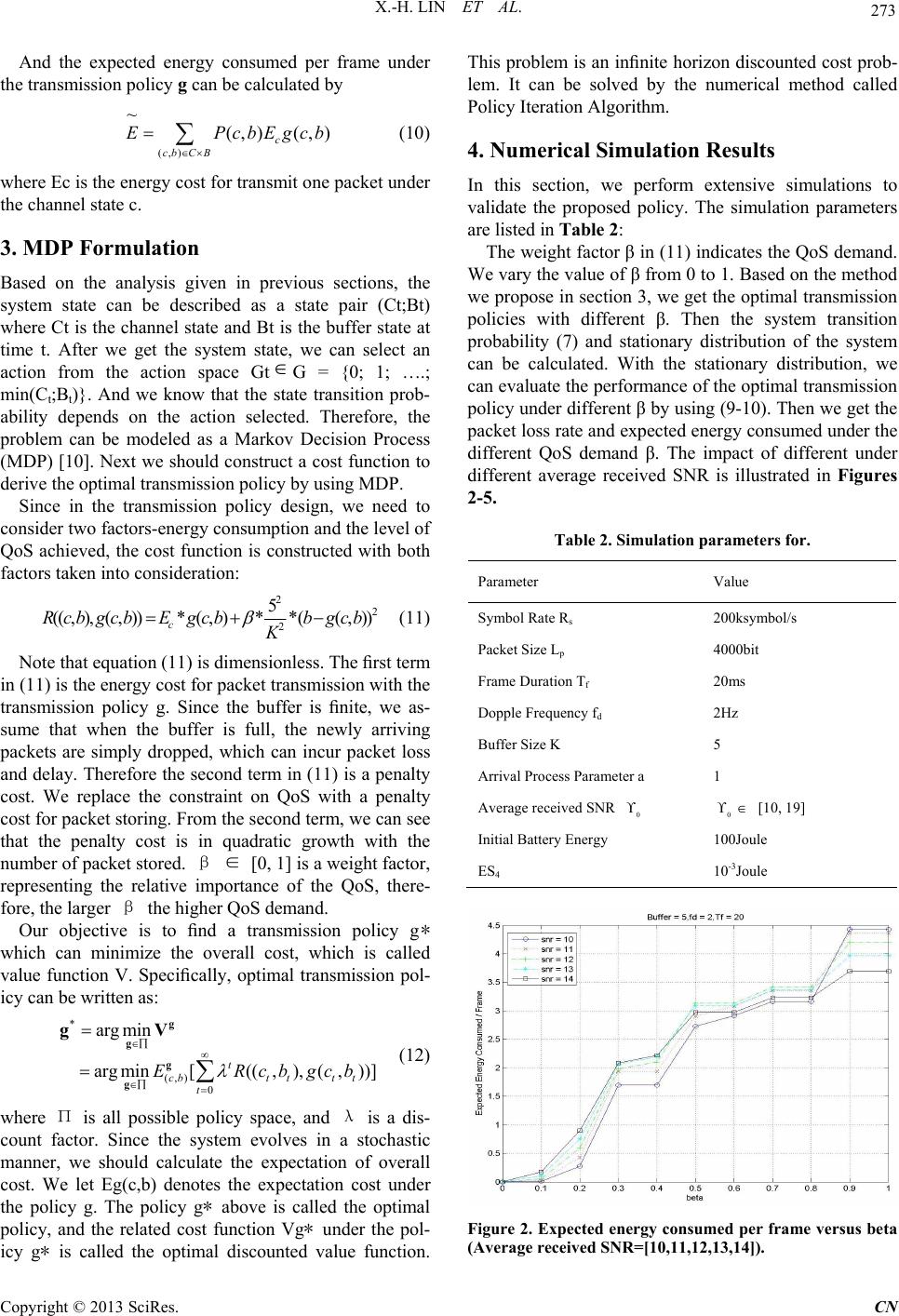

X.-H. LIN ET AL. 273
And the expected energy consumed per frame under
the transmission policy g can be calculated by
(,)
~
(, )(, )
c
cbC B
E PcbEgcb

 (10)
where Ec is the energy cost for transmit one packet under
the channel state c.
3. MDP Formulation
Based on the analysis given in previous sections, the
system state can be described as a state pair (Ct;Bt)
where Ct is the channel state and Bt is the buffer state at
time t. After we get the system state, we can select an
action from the action space GtG = {0; 1; ….;
min(Ct;Bt)}. And we know that the state transition prob-
ability depends on the action selected. Therefore, the
problem can be modeled as a Markov Decision Process
(MDP) [10]. Next we should construct a cost function to
derive the optimal transmission policy by using MDP.

Since in the transmission policy design, we need to
consider two factors-energy consumption and the level of
QoS achieved, the cost function is constructed with both
factors taken into consideration:
2
2
2
5
((, ),(, ))*(,)**((, ))
c
R cbgcbEgcbbgcb
K
  (11)
Note that equation (11) is dimensionless. The first term
in (11) is the energy cost for packet transmission with the
transmission policy g. Since the buffer is finite, we as-
sume that when the buffer is full, the newly arriving
packets are simply dropped, which can incur packet loss
and delay. Therefore the second term in (11) is a penalty
cost. We replace the constraint on QoS with a penalty
cost for packet storing. From the second term, we can see
that the penalty cost is in quadratic growth with the
number of packet stored. β ∈ [0, 1] is a weight factor,
representing the relative importance of the QoS, there-
fore, the larger β the higher QoS demand.
Our objective is to find a transmission policy g∗
which can minimize the overall cost, which is called
value function V. Specifically, optimal transmission pol-
icy can be written as:
*
(,)
0
arg min
argmin[((,),(,))]
t
cbtt tt
t
ERcbgcb 
 
 


g
g
g
g
gV
(12)
where Π is all possible policy space, and λ is a dis-
count factor. Since the system evolves in a stochastic
manner, we should calculate the expectation of overall
cost. We let Eg(c,b) denotes the expectation cost under
the policy g. The policy g∗ above is called the optimal
policy, and the related cost function Vg∗ under the pol-
icy g∗ is called the optimal discounted value function.
This problem is an infinite horizon discounted cost prob-
lem. It can be solved by the numerical method called
Policy Iteration Algorithm.
4. Numerical Simulation Results
In this section, we perform extensive simulations to
validate the proposed policy. The simulation parameters
are listed in Table 2:
The weight factor β in (11) indicates the QoS demand.
We vary the value of β from 0 to 1. Based on the method
we propose in section 3, we get the optimal transmission
policies with different β. Then the system transition
probability (7) and stationary distribution of the system
can be calculated. With the stationary distribution, we
can evaluate the performance of the optimal transmission
policy under different β by using (9-10). Then we get the
packet loss rate and expected energy consumed under the
different QoS demand β. The impact of different under
different average received SNR is illustrated in Figures
2-5.
Table 2. Simulation parameters for.
Parameter Value
Symbol Rate Rs 200ksymbol/s
Packet Size Lp 4000bit
Frame Duration Tf 20ms
Dopple Frequency fd 2Hz
Buffer Size K 5
Arrival Process Parameter a 1
Average received SNR 0

0  [10, 19]
Initial Battery Energy 100Joule
ES4 10-3Joule
Figure 2. Expected energy consumed per frame versus beta
(Average received SNR=[10,11,12,13,14]).

X.-H. LIN ET AL.
274
Figure 3. Expected energy consumed per frame versus beta
(Average received SNR =[15,16,17,18,19]).
Figure 4. Packet loss rate versus beta(Average received
SNR = [10, 11, 12,13, 14]).
Figure 5. Packet loss rate versus beta (Average received
SNR = [15, 16, 17,18, 19]).
In the Figure2-3 we can observe that the expected en-
ergy consumed per frame increases with β, which indi-
cates that when the QoS demand increases, the penalty
for buffering the packet increases as well. It is unwise to
store the packet in buffer, because the storing cost is
higher than that of transmission cost, even we transmit
the packet under a low mode. Hence system should
transmit packet as much as possible no matter what
transmit mode it would adopt. However when become
small, the storing cost is relatively smaller than the
transmit cost. Therefore, system would prefer packet
storing rather than transmission, and wait until the chan-
nel quality recover.
From the Figures 4-5 we can observe that the packet
loss rate decreases with β, which means that by varying
β , we can achieve different levels of QoS. Joint with
Figures 2-3 we can see the tradeoff between energy and
QoS, i.e. Higher energy consumption means a better
QoS.
Next, we compare our Energy-Efficient Transmission
Policy (EETP) with Threshold Transmission Policy (TTP)
[8].
The average received SNR = 15dB. Under the Thresh-
old Transmission Policy, only when the received SNR is
above the threshold Ak can we transmit packets. The
system transmits packet in a best effort manner. Then we
have 4 different transmission policies under the Thresh-
old Transmission Policy, among which, we can select the
best one.
However, compared with TTP, more policy strategies
are provided in our method, and thus search space is
much larger. Consequently, we can further reduce the
energy consumption with better policy as illustrated in
Figure 6.
Figure 6. Energy Efficient Transmission Policy versus
Threshold Transmission Policy.

X.-H. LIN ET AL.
275
5. Conclusions
In this paper, we study the energy efficient transmission
under the constant transmission power constraint. We
formulate the Energy Efficient Transmission Problem as
a MDP problem and use the Policy Iteration Algorithm to
get the optimal transmission policy which consumes the
least amount of energy while achieving the QoS demand.
We compare our method with previous threshold method.
Simulation results show that our transmission policy can
reduce the energy consumption significantly.
6. Acknowledgements
The research was jointly supported by research grant
from Natural Science Foundation of China under project
number 61171071, 60602066, 60902016, 61001182 and
60773203, 973 Program under the project number
2013CB336700, and grants from Foundation of Shen-
zhen City under project number JC200903120069A,
JC201005280556A, JC201005250035A,
JC201005250047A, JCYJ20120613115037732, and
ZDSY20120612094614154. The Corresponding author
of the paper.
REFERENCES
[1] E. Uysal-Biyikoglu, B. Prabhakar and A. El Gamal, ”En-
ergy Efficient Packet Transmission over a Wireless
Link,” IEEE/ACM Transactions on Networking, Vol. 10,
2002, pp. 487-499. doi:10.1109/TNET.2002.801419
[2] S. Curt, R. Vijay and B. S. Mani, “Power Management
for Energy-aware Communication Sincerely yours, ys-
tems.” Vol. 2, 2003, pp. 431-447.
[3] B. Ata, “Dynamic Power Control in a Wireless Static
Channel Subject to a Quality-of-Service Constraint,” Op-
erations Research, Vol. 53, 2005, pp. 842-851.
doi:10.1287/opre.1040.0188
[4] L. Qingwen, Z. Shengli and G. B. Giannakis, “Queuing
with Adaptive Modulation and Coding over Wireless
Links: Cross-Layer Analysis and Design,” IEEE Trans-
actions on Wireless Communications, Vol. 4, 2005, pp.
1142-1153. doi:10.1109/TWC.2005.847005
[5] J. Razavilar, K. J. R. Liu, and S. I. Marcus, “Jointly opti-
mized bit-rate/delay control policy for wireless packet
networks with fading channels,” IEEE Transactions on
Communications, Vol. 50, 2002, pp. 484-494.
doi:10.1109/26.990910
[6] H. Xinwei and K. Shoraby, “A Dynamic Programming
Approach for Optimal Scheduling Policy in Wireless
Networks,” In Proceeding of. Eleventh International Con-
ference on Computer Communications and Networks,
2002, pp. 530-536.
[7] W. H. Shen and N. Moayeri, “Finite-state Markov Chan-
nel Model for Radio Communication Channels,” IEEE
Transactions on Vehicular Technology, Vol. 44, 1995, pp.
163-171.doi:10.1109/25.350282
[8] X. –H. Lin, K. Yu-Kwong and W. Hui, “Cross-layer De-
sign for Energy Efficient Communication in Wireless
Sensor Networks,” Vol. 9: John Wiley and Sons Ltd.,
2009, pp. 251-268.
[9] C. S. Taek and A. J. Goldsmith, “Degrees of Freedom in
Adaptive Modulation: A Unified View,” IEEE Transac-
tions on Communications, Vol. 49, 2001, pp. 1561-1571.
doi:10.1109/26.950343
[10] M. L. Puterman, Dynamic Programming, 3rd ed. Vol 4,
2002.