Communications and Network, 2013, 5, 255-259
http://dx.doi.org/10.4236/cn.2013.53B2047 Published Online September 2013 (http://www.scirp.org/journal/cn)
Transmission Scheduling Algorithm in DTN
Wei Yu1, Hongyan Li1, Jiandong Li1, Lin Jin1, Kun Yuan2
1State Key Laboratory of Integrated Service Networks1,Xidian University, Xi’an, China
2Department of Automation2, University of Science and Technology of China, Hefei, Anhui, China
Received June, 2013
ABSTRACT
Delay Tolerant Networks (DTNs) is a dynamic topology network, in which connection durations of each link are vari-
able and paths between two nodes are intermittent. Most of protocols which are widely used in traditional wireless net-
work are not suitable for DTNs. DTN adopts store-and-forward mechanism to cope with the problem of intermittent
path. With limited storage of each node, it is a challenge for scheduling nodes’ transmission to avoid overflow of nodes’
buffers. In this paper we propose an optimal transmission scheduling algorithm for DTN with nodes’ buffer cons traints.
The object of the optimal algorithm is to get maximum throughput. We also present an algorithm for obtaining subop-
timal transmission schedules. Our solution is certified through simulation, and it is observed that our solution can im-
prove network per formance in the aspects of avoiding overfl ow and i ncreas i ng net w o rk th ro ugh p ut.
Keywords: DTN; Transmission Scheduling Algorith m; Throughput; Overflow
1. Introduction
Delay-Tolerant Networks (DTNs) [1] has characteristics
of constrained storage, high delay and intermittent con-
nections, which lead to no existence of end-to-end path
between source and destination at most times. DTN ap-
proaches this problem with store-and-forward mecha-
nism. The nodes, existing in the system operating on
aforementioned mechanism, firstly store messages re-
ceived from the upstream ones, and then wait for connec-
tion of outgoing links to send stored messages out. It's
very challenging for relay nodes with limited storage.
Once the amount of stored messages meets the upper
bound of storage, overflow potentially happens in the
relay nodes due to a period of outgoing link disconnec-
tions. Since there is not enough storage space for new
messages, relay nodes have to refuse new messages or
discard old ones, causing energy waste and throughput
decrease.
Although DTN networks are always mobile, in most
cases, the node movements can be known in advance be-
cause of their predictable trajectories. There have been a
lot of DTN studies based on prediction [2-4]. Consider an
example deterministic network of five nodes 121 2 {,
as shown in Figure 1, in which contact times are known
or can be explicitly predicted. Contact times among the
five nodes are shown in Figure 2(a), in which 1 and
are connected from to , and a link exists
between R and D1 from to . Contact time
between and is [6 , and the one between R
and D2 is [7,9].
,, ,}SSRDD
S
R2t10t
,8]
5t
t13
2
SR
Messages in 1 need to be transmitted to 1, but
there isn't an end to end path between them. So the mes-
sages should be firstly offloaded from 1 to R in their
contact time [2,5] and then wait at R until
S D
10
St

, when
the connection between R and 1 begins. Similarly, 2
sends messages to R at D S
6t

and R relays messages to
2 at D7t

. All the link rates are set to 1. Message
forwarding sequences 11
{, and 22 {, are
marked as path1 and path2 respectively. Contacts be-
tween nodes on both paths are periodic and the least
common multiple of their periods is 14. Their periodicity
isn't shown in Figure 2 due to lack of space. The occupa-
tion of messages on R 's storage space has been depicted
in Figure 3(a) with the storage of R unlimited. If the
upper storage bound of R is set to 3, R is full at
,D}SR ,D
t
}SR
5

and only until 10t

able it is to free its storage as shown
in Figure 3(b). So 2 cannot send messages to R since
their contact time begins at and ends at t
S6t8

.
Under this situation, the contact times which can be util-
ized are shown in Figure 2(b) and the theoretical average
network throughput is 0.214, i.e. . But
if the contact time between and R is replaced with
1 (52) \140. 214
1
S
Figure 1. Network topology.
C
opyright © 2013 SciRes. CN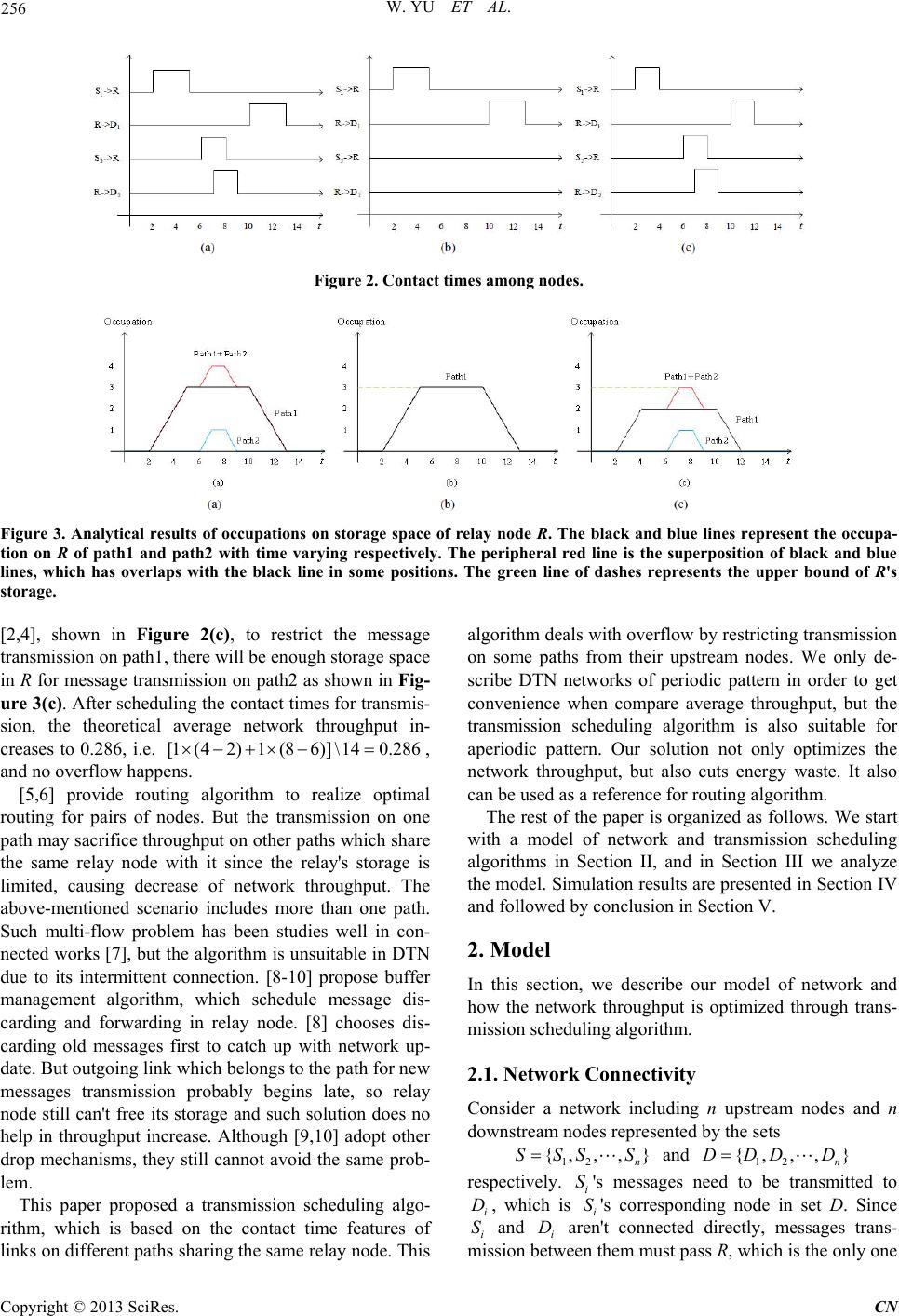

W. YU ET AL.
256
Figure 2. Contact times among nodes.
Figure 3. Analytical results of occupations on storage space of relay node R. The black and blue lines represent the occupa-
tion on R of path1 and path2 with time varying respectively. The peripheral red line is the superposition of black and blue
lines, which has overlaps with the black line in some positions. The green line of dashes represents the upper bound of R's
storage.
[2,4], shown in Figure 2(c), to restrict the message
transmission on path1, there will be enough storage space
in R for message transmission on path2 as shown in Fig-
ure 3(c). After scheduling the contact times for transmis-
sion, the theoretical average network throughput in-
creases to 0.286, i.e. ,
and no overflow happens.
[1 (42)1 (86)]\140.286
[5,6] provide routing algorithm to realize optimal
routing for pairs of nodes. But the transmission on one
path may sacrifice throughput on other paths which share
the same relay node with it since the relay's storage is
limited, causing decrease of network throughput. The
above-mentioned scenario includes more than one path.
Such multi-flow problem has been studies well in con-
nected works [7], but the algorithm is unsuitable in DTN
due to its intermittent connection. [8-10] propose buffer
management algorithm, which schedule message dis-
carding and forwarding in relay node. [8] chooses dis-
carding old messages first to catch up with network up-
date. But outgoing link which belongs to the path for new
messages transmission probably begins late, so relay
node still can't free its storage and such solution does no
help in throughput increase. Although [9,10] adopt other
drop mechanisms, they still cannot avoid the same prob-
lem.
This paper proposed a transmission scheduling algo-
rithm, which is based on the contact time features of
links on different paths sharing the same relay node. This
algorithm deals with overflow by restricting transmission
on some paths from their upstream nodes. We only de-
scribe DTN networks of periodic pattern in order to get
convenience when compare average throughput, but the
transmission scheduling algorithm is also suitable for
aperiodic pattern. Our solution not only optimizes the
network throughput, but also cuts energy waste. It also
can be use d as a reference f or routin g algorithm.
The rest of the paper is organized as follows. We start
with a model of network and transmission scheduling
algorithms in Section II, and in Section III we analyze
the model. Simulation results are presented in Section IV
and followed by con clusion in Section V.
2. Model
In this section, we describe our model of network and
how the network throughput is optimized through trans-
mission scheduling algorithm.
2.1. Network Connectivity
Consider a network including n upstream nodes and n
downstrea m nodes represented b y the sets
12
{,,, }
n
SSSS

 and
12
{,,, }
n
DDDD
respectively. 's messages need to be transmitted to
, which is i's corresponding node in set D. Since
i and i aren't connected directly, messages trans-
mission between them must pass R, which is the only on e
i
SS
i
D
S D

W. YU ET AL. 257
relay node in this network. So there are n ingoing links
and n outgoing links. These links can be represented by
link function which can show whether the link exists or
not. Link function is defined for ingoing link
between i and R, and is for outgoing link
between R and i. Let 
denote the contact
time between i and R in a period of T. i and R can
communicate to each other since ingoing link exists dur-
ing insine
. Similarly, [,
sout e
denotes the
contact time between R and . We can define
and as:
()
i
in
Lt
0[
s
out s
tt
hersin
tt
othersin




()
ii
in in
ii
out out
vL
vL
11
},{ ,S
i
SR
S
[,
ii
tt

()t
()
()
Lt
Lt
()
in
vt
()t
i
in
{{
ii
tt
()
i
out
Lt
[,
ii
in sine
tt

out
i
D
0,
0[
ii
in e
ii
out e
t
T
t
T


()
i
i
t i
ti


2
, },RD
{,,
i
SR
ii
tt
()
i
D
]
1
in
ot
()t
()
()vt
, ,RD
]t
]
S
1






out
v
in
out
vt
S

S
]
, ,
,2,


,
n
n
,
nn
RD
12
,p
/
i
v
]
i
v
ii
tt

]
0,
i
1,
1,
2

D

i
RD
t
()
i
in
Lt
n


SR
SR
}
t
i
out
L
i
in
i
out
i
i
out
v
)ti
v
i
out
v
P
1,2
1
]
i
i
RD
2, ,
2,


{ ,S
}
i
{,Pp
SR
iin
tv
/
i
v
,
n
(1)
Let denote rate function for ingoing link i,
and is for outgoing link . Rate function
and are defined as: (
i
in
v
where is the rate of connected ingoing link i,
and is the rate of connected outgoing link .
i
It is noted that there are n forwarding sequences, which
can be represented by the set
RD
}}
in this network. Sequence is marked as path
, so we can also present P as .
i
pn p
2.2. Optimal Transmission Scheduling
Algorithm
In this paper, our algorithm is able to avoid overflow in
relay node and increase network throughput by altering
lengths of contact times between nodes. We assume that
all the messages received by R can be sent out in the pe-
riod of T, i.e. each outgoing link can undertake transmis-
sion task from its corresponding ingoing link. Let i
denote the length of ingoing link i's contact time is
shortened by. Accordingly, the length of outgoing link
i's contact time is shortened by out to meet
the aforementioned assumption. Therefore the original
contact times of links and in (1) are changed
into [,
in sin ei and [, out soutei inout respectively.
The most important constraint here is that the sum of
each path's occupation on R must be less than R's maxi-
mal storage at any time. Let
RD i
f
t denote i's occupa-
tion functi o n o n R. Expression of p
()
i
f
t is as follow:
0[
t
() ()
in ()]
ii
out 0
i
f
tv
tvtdt tT
Therefore, the linear program computed the maximal
network throughput is resulted as follow: Th
0
1
11 122 2
12
max
0
1
1
max( )
1
=[() ()
()]
..()[ ()()]
0
nTi
in
i
ininein sininein s
nnn
ininein sn
nTii R
in out
i
ii
iineins
Thvt dt
T
vt t tvt t t
T
vttt
stf tvtvtdtC
tt t

 




 
 

 


(2)
where ()
f
t is a function representing the sum of all
paths' occupation functions on R, and max
R
C is R's
maximal storage.
It is important to note that this linear program is hard
to solve due to its complex constraint, which must guar-
antee no overflow at anytime. So we also propose a sim-
plified algorithm called transmission scheduling algo-
rithm (TSA).
2.3. Transmission Scheduling Algorithm
We simplify this problem by assuming that ()
f
t only
has one maximum beyond max
R
C during the period of T
under the assumption of unlimited storage of R, that is i
for t
1, 2,,in


) in (2). Let t denote the time when (
f
t reaches its maximum, which is also the maximal
value of ()
f
t. So t must satisfy the following inequality:
**
()()0,0
f
tft tTtT
Therefore when the storage of R is set to max
R
C, the
overflow can be figured out as follow:
over
C
*max
()
R
over
CftC
We shorten the contact times to decrease the sum of
message transmission of all ingoing links by . We
certainly make sure the real-time value of over
C
()
f
t is no
more than max
R
C
t
i
in e
in this way. The shortening process is
realized by wiping a part off each contact time in (1).
The length of contact time shortened by is also repre-
sented as i, which has the same meaning as in the linear
program of (2). It is important to notice that the end time
of the wiped part must be earlier than t, otherwise such
shortening makes no contribution to overflow avoiding.
Therefore the wiped part of ingoing link's contact time
can be presented as in e iin. That
is if
**
[min( ,),min(tt tt, )]
ii
e
t

*
tt


in s
, change the contact time of link i in (1)
into i
SR
[,]
ii
in e
tt

t

, otherwise change it into two parts,
*
[,
s
tt ]t
i
in i

and . Accordingly, the contact
time of outgoing link i in (1) is changed into
out soutei inout  . Therefore the linear program of
(2) can be simplified as follow:
*
[, ]
i
in e
tt
RD
/]
i
v[,
ii
tt i vt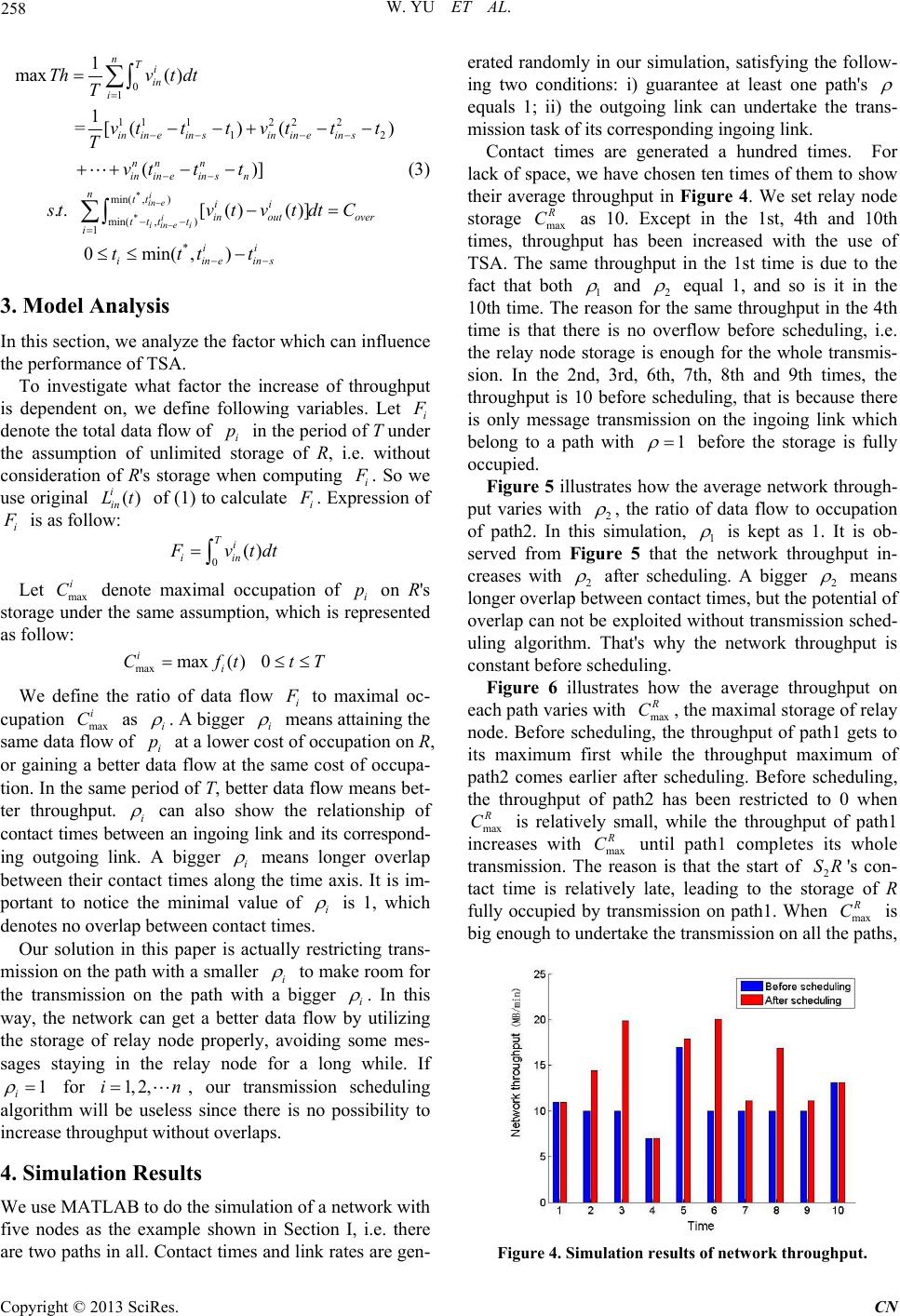

W. YU ET AL.
258
*
*
0
1
11 122 2
1
min( ,)
min( ,)
1
*
1
max( )
1
=[() ()
()]
..[ ()()]
0min(,)
i
in e
i
iinei
nTi
in
i
ininein sininein s
nnn
ininein sn
ntt ii
in outover
ttt t
i
ii
iineins
Thvt dt
T
vt t tvt t t
T
vttt
stvtvtdtC
tttt



 





 
 

 



2
(3)
3. Model Analysis
In this section, we analyze the factor which can influence
the performance of TSA.
To investigate what factor the increase of throughput
is dependent on, we define following variables. Let i
F
denote the total data flow of i in the period of T under
the assumption of unlimited storage of R, i.e. without
consideration of R's storage when computing i
p
F
. So we
use original of (1) to calculate ()
i
in
Lt i
F
. Expression of
i
F
is as follow:
0()
i
ii
n
T
F
vtdt
Let max denote maximal occupation of i on R's
storage under the same assumption, which is represented
as follow:
i
Cp
max max( )0
ii
CfttT
We define the ratio of data flow i
F
to maximal oc-
cupation max as
i
Ci

. A bigger i

means attaining the
same data flow of i at a lower cost of occupation on R,
or gaining a better data flow at the same cost of occupa-
tion. In the same period of T, better data flow means bet-
ter throughput. i
p

can also show the relationship of
contact times between an ingoing link and its correspond-
ing outgoing link. A bigger i

means longer overlap
between their contact times along the time axis. It is im-
portant to notice the minimal value of i

is 1, which
denotes no overlap between contact tim es.
Our solution in this paper is actually restricting trans-
mission on the path with a smaller i

to make room for
the transmission on the path with a bigger i

. In this
way, the network can get a better data flow by utilizing
the storage of relay node properly, avoiding some mes-
sages staying in the relay node for a long while. If
1
i

 for , our transmission scheduling
algorithm will be useless since there is no possibility to
increase throughput without overlaps.
1, 2, in
4. Simulation Results
We use MATLA B to do the simulation of a network with
five nodes as the example shown in Section I, i.e. there
are two paths in all. Contact times and link rates are gen-
erated randomly in our simulation, satisfying the follow-
ing two conditions: i) guarantee at least one path's

equals 1; ii) the outgoing link can undertake the trans-
mission task of its corresp onding ingoing link.
Contact times are generated a hundred times. For
lack of space, we have chosen ten times of them to show
their average throughput in Figure 4. We set relay node
storage max
R
C as 10. Except in the 1st, 4th and 10th
times, throughput has been increased with the use of
TSA. The same throughput in the 1st time is due to the
fact that both 1

and 2

equal 1, and so is it in the
10th time. The reason for the same throughput in the 4th
time is that there is no overflow before scheduling, i.e.
the relay node storage is enough for the whole transmis-
sion. In the 2nd, 3rd, 6th, 7th, 8th and 9th times, the
throughput is 10 before scheduling, that is because there
is only message transmission on the ingoing link which
belong to a path with 1


before the storage is fully
occupied.
Figure 5 illustrates how the average network through-
put varies with 2

, the ratio of data flow to occupation
of path2. In this simulation, 1

is kept as 1. It is ob-
served from Figure 5 that the network throughput in-
creases with 2

after scheduling. A bigger 2

means
longer overlap between contact times, but the potential of
overlap can not be exploited without transmission sched-
uling algorithm. That's why the network throughput is
constant before scheduling .
Figure 6 illustrates how the average throughput on
each path varies with max
R
C, the maximal storage of relay
node. Before scheduling, the throughput of path1 gets to
its maximum first while the throughput maximum of
path2 comes earlier after scheduling. Before scheduling,
the throughput of path2 has been restricted to 0 when
max
R
C is relatively small, while the throughput of path1
increases with max
R
C until path1 completes its whole
transmission. The reason is that the start of 2's con-
tact time is relatively late, leading to the storage of R
fully occupied by transmission on path1. When max
SR
R
C is
big enough to undertake the transmission on all the paths,
Figure 4. Simulation results of netw ork throughput.

W. YU ET AL.
259
This algorithm takes intermittent connection and con-
strained storage of DTN into consideration. In the future,
we want to analyze how high delay will affect this
transmission scheduling algorithm, and optimize the al-
gorithm in order to apply it in more complex DTN sce-
narios.
6. Acknowledgements
This work is supported by the National Science Founda-
tion (60972047, 61231008), National S\&T Major Pro-
ject (2011ZX03005-004, 2011ZX03004-003, 2011ZX-
03005-003-03, 2013ZX03004007-003), Shaanxi 13115
Project(2010ZDKG-26), National Basic Research Pro-
gram of China (2009CB320404), Program for Changji-
ang Scholars and Innovative Research Team in Univer-
sity(IRT0852), the 111 Project (B08038) and State Key
Laboratory Foun datio n (IS N 10 0 200 5, IS N0 90 3 05 ).
Figure 5. Simulation results of network throughput with
1

fixed to 1 and 2

varying.
REFERENCES
[1] K. Fall, “A Delay Tolerant Network Architecture for
Challenged Internets,” in Proceedings of ACM SIGCOM
pp. 27-24, 2003.
[2] S. Merugu, M. Ammar and E. Zegura, “Routing in Space
and Time in Networks with Predictable Mobility,” Geor-
gia Institute of Technology, Tech. Rep., 2004.
Figure 6. Simulation results of each path's throughput wi th
varying.
R
Cmax
[3] J. Francois and G. Leduc, “Routing Based on Delivery
Distributions in Predictable Disruption Tolerant Net-
works,” Ad-Hoc Networks, Vol. 7, No. 1, 2009, pp.
219-229. doi:10.1016/j.adhoc.2008.02.006
the throughput of path2 will increases with max
R
C until
the maximal value it can reach. [4] M. Huang, S. Chen, Y. Zhu, et al., “Topology Control for
Time-evolving and Predictable Delay-tolerant Networks,”
in IEEE MASS, 2011.
After scheduling, transmission on either paths may be
restricted when max
R
C is relatively small. The reason is
that max
R
C is too small to undertake the transmission
during the co ntact time befo re over lap adv ents, so wip ing
contact time from either path will lead to the same net-
work throughput. With the increase of max
R
C, transmis-
sion scheduling algorithm will choose to leave storage to
path2 first by restricting transmission on path1 since 2

is bigger than 1

, and the throughput of path2 increases
with max
R
C until path2 completes its whole transmission.
When max
R
C
max
is big enough to undertak e the transmission
on all the paths, the throughput of path1 will increases
with
R
C until the maximal value it can reach.
[5] S. Jain, K. R. Fall and R. K. Patra, “Routing in a Delay
Tolerant Network,” in ACM SIGCOMM, 2004, pp.
145-158.
[6] D. Hay and P. Giaccone, “Optimal Routing and Schedul-
ing for Deterministic Delay Tolerant Networks[C]” Wire-
less On- Demand Network Systems and Services, 2009.
WONS 2009. Sixth International Conference on. IEEE,
2009, pp. 27-34.
[7] I. Chlamtac, A. Farag’o, H. Zhang and A. Fumagalli, “A
Deterministic Approach to the end-to-end Analysis of
Packet Flows in Connection Oriented Networks,” IEEE/
ACM Transactions on Networking, Vol. 6, 1998, pp.
4422-4431.
[8] V. N. G. J. Soares, J. J. P. C. Rodrigues, P. S. Ferreira and
A. M. D. Nogueira, “Improvement of Messages Delivery
time on Vehicular Delay-tolerant Networks,” in Interna-
tional Conference on Parallel Processing Workshops (pp.
344-349). IEEE. 2009.
5. Conclusions
In this paper, we propose a transmission scheduling algo-
rithm by simplifying optimal algorithm in DTN, which is
able to avoid overflow, increase network throughput and
save node energy. Our algorithm is validated by com-
puter simulation. It is observed that this algorithm assur-
edly increases network performance since it can take
good advantage of constrained storage of relay node by
roperly assigning it to different paths.
[9] S. Rashid, Q. Ayub, “Effective Buffer Management Pol-
icy DLA for DTN Routing Protocals under Congestion,”
International Journal of Computer and Network Security,
Vol. 2, No. 9, 2010. pp. 118-121.
[10] S. Rashid, et al.,“E-DROP: An Effective Drop Buffer
Management Policy for DTN Routing Protocols,” Inter-
national Journal, 2011, Vol. 13, No. 7, pp. 8-13. p