Communications and Network, 2013, 5, 238-244
http://dx.doi.org/10.4236/cn.2013.53B2044 Published Online September 2013 (http://www.scirp.org/journal/cn)
Power Allocation in Primary User-Assisted Multi-Channel
Cognitive Radio Networks
Qiong Wu, Junni Zou, Kangning Zhu
Department of Communication Engineering, Shanghai University, Shanghai, China
Received June, 2013
ABSTRACT
This paper addresses power allocation problem for spectrum sharing multi-band cognitive radio networks, where the
primary user (PU) allows secondary users (SUs) to transmit simultaneously with it by coding SU's signal together with
its own signal. The PU acts as the relay for the SUs and sells its transmit power to the SUs to increase its benefit, and
the SUs bid for the PU's transmit power for maximizing their utilities. We propose a power allocation scheme based on
traditional ascending clock auction, in which the SUs iteratively submit the optimal power demand to the PU according
to the PU's announced price, and the PU updates that price based on all SUs' total power demands. Then we mathe-
matically prove the convergence property of the proposed auction algorithm (i.e., the auction algorithm converges in a
finite number of clocks), and show that the proposed power auction algorithm can maximize the social welfare. Finally,
the performance of the proposed scheme is verified by the simulation results.
Keywords: Power Allocation; Cognitive Radio ; Auction; Cooperative Communications
1. Introduction
With the rapid deployment of wireless services in the last
decade, the scarcity in radio spectrum emerges a critical
issue for wireless communications. However, the report
from the Federal Communications Commissions shows
that most of the licensed spectrum is severely underuti-
lized in traditional fixed spectrum allocation [1]. Cogni-
tive radio (CR) is a technology that can deal with the
dilemma between spectrum scarcity and spectrum under-
utilization [2]. It allows the unlicensed users (secondary
users (SUs)) to access licensed bands owned by the li-
censed users (primary users (PUs)) without interfering
with them.
As described in [3], SUs can access the spectrum
owned by the primary user using spectrum sharing,
where the SU coexists with the PU and transmits with
power constraints to guarantee the quality of service
(QoS) of the PU. To improve the efficiency of resource
utilization, cooperative communications has been intro-
duced in CR networks. In [4], the SU transmitter allo-
cates only part of its power to deliver its own messages,
and uses the remaining power to forward PU’s messages
so as to compensate the interference at the PU receiver.
A dynamic spectrum leasing architecture was proposed
in [5], which allows PUs to reduce their power expendi-
ture by using the SUs as relay nodes. The authors in [6]
formulated the resource allocation problem as a two-tier
game, in which each PU acts as a relay for multiple SUs
and sells the unused radios to SUs. However, the studies
in the literature on PU-assisted cooperative communica-
tions in spectrum sharing CR networks are still relatively
sparse, and how to control the transmit power at the PU
for secondary transmissions remains an open problem.
Network Coding has been proved to be a promising
approach to reduce time-slot overhead for cooperative
communications in wireless networks [7]. In [8], the ex-
change of independent information between two nodes in
a wireless network has been analyzed. It demonstrated
that information exchange can be efficiently performed
by exploiting network coding and the broadcast nature of
the wireless medium. The authors in [9] addressed the
power allocation problem in a network-coded multiuser
two-way relaying network, where multiple pairs of users
communicate with their partners via a common relay
node. In cognitive radio networks, the authors in [10]
showed that distributed network users can automatically
adjust their coding structure, then collaborate together to
avoid the degrading effects of signal fading. In this study,
we consider the scenario that PU helps SUs by forward-
ing their combining signals to improv e transmission effi-
ciency.
The researches on power control for CR networks
have been conducted most recently [11-13]. Most exist-
ing studies focused on centralized schemes that often
need high requirements on network infrastructure, and
their computational complexity scales up with the net-
C
opyright © 2013 SciRes. CN

Q. WU ET AL. 239
work size. Game theory has been widely recognized as a
powerful tool for distributed resource allocation in inter-
active multiuser systems. In order to address both system
efficiency and user fairness issues of CR networks, the
authors in [14] proposed a distributed power control
strategy by using a cooperative Nash bargaining game
model. In [15], a joint power and rate control strategy
were presented for SUs on the basis of a cooperative
game theoretic framework. Three auction-based schemes
were proposed in [16] for multimedia streaming over CR
networks. In [17], the authors considered auction-based
power allocation in multi-band CR networks, wh ere mul-
tiple SUs transmit via a common relay, and bid for the
transmit power of the relay.
In this paper, we consider the power allocation prob-
lem for spectrum sharing multi-band CR networks, where
the PU allows the SUs to transmit simultaneously with it
by coding SU’s signal together with its own signal. The
PU acts as the relay for the SUs and sells its transmit
power to the SUs to increase its benefit, and the SUs b id
for the PU’s transmit power for maximizing their utilities.
Our main contributions are as follows: First, we propose
a power allocation scheme based on traditio nal ascending
clock auction (ACA-T), in which the SUs iteratively
submit the optimal power demand to the PU according to
the PU’s announced price, and the PU updates that price
based on all SUs’ total power demands. Second, we
mathematically prove the convergence property of the
proposed auction algorithm (i.e., the auction algorithm
converges in a finite number of clocks), and show that
the proposed power auction algorithm can maximize the
social welfare. Finally, the performance of the proposed
scheme is verified by the simulation results.
2. Network Modeling and Notations
Consider a CR system consisting of a primary user di-
vided into M non-overlapping narrowband subchannels
and N secondary users. The primary user transmits sig-
nals from the primary transmitter (PT) to the primary
receiver (PR). Each secondary user i sends messages
from secondary transmitter si to secondary receiver di.
The PT acts as the relay and assists SUs’ transmissions.
We employ analog network coding and the amplify-and-
forward relaying protocol at the PT. Assume that each
sub-channel of the PT can be accessed by only one SU,
and the channel occupancy by the SUs is maintained by
the PT. For simplicity, we consider the scenario where
N=M. The cases with N < M and N > M can be analyzed
in a similar way.
The structure of a CR frame under spectrum sharing
consists of a channel allocation slot, an auction slot and a
data transmission slot. In chan nel allocation slot, the SUs
who intend to send data to their receivers submit their
transmission requests to the PT. The PT then randomly
assigns a sub-channel to each SU. As shown in Figure 1,
SU i is designated to the jth sub-channel of the PT, and
the transmission time period is divided into three phases.
Here the solid lines indicate the intended communica-
tions, while the dotted lines represent the interferen ce.
In the first phase: At each sub-channel, the PT trans-
mits its data to its destinatio n PR with power Pu. Assume
that the total transmit power of the PT is Pt, then we have
Pu=Pt/M. As in the wireless environment, the data will
be transmitted in a broadcast way, so all the receivers in
the system will overhear and receive the data. The sig-
nals received at the PR and the secondary receivers are
respectivel y given by
P
RPRPR
P
TuPTu
YPGXnPT  (1)
ii
dd
i
d
P
TuPTu
YPGXnPT  (2)
where {}
{}
Y



represents the signal received at {}

 from
{}

, Xu is the information symbol transmitted by PT
with 2
| ]1[|u EX

, {}
{}
n



is the additive white Gaussian
noise (AWGN) with variance 2

. And {}
{}
G



denotes
the fading channel gain from to {, where its am-
plitude is exponentially distributed. Assume all
the channel gains remain static during each transmission
frame, and are available to the PT.
{}}
{} 2
|
{}
|G

The signal-to-interference-plus-noise-ratio (SINR) of
Xu at the PT in the first phase is
2
(1) /
PR PR
PTu PT
PG

 (3)
In the second phase: SU i transmits its signal with
power Pi. The signals received by di, PT and PR are
ii
i ii
dd
is
i
i
d
s
s
YPGXns  (4)
iiii
P
TPTPT
s
is ss
YPGXn (5)
iiii
P
RPRPR
s
is ss
YPGXn
(6)
where i
s
X
is the signal transmitted by si in this phase
with 2
| ]1
i
[| s EX

.
Figure. 1. Transmissions in three phases.

Q. WU ET AL.
240
Thus, the SINR of i
s
X
at SR di in the second phase is
2
(2) /
ii
ii
dd
i ss
PG

 (7)
In the third phase: In this case, the PT makes a com-
bination of i
Y
P
T
s
and its own signal Xu with network
coding [18], then amplifies and forwards the combined
signal Xi-NC. Then the received signals are
P
RPRPR
P
TNCui PTiNCPT
YPGX

n (8)
ii
dd
i
d
P
TNCui PTiNCPT
YPGX

n (9)
where {}
{}
N
C
Y
 represents the signal received by using net-
work coding, Pui is the PT’s transmit power for SU i, and
||
i
i
PT
us
iNC PT
us
XY
XXY


 (10)
Substituting (5) into (10), we can rewrite (8) and (9) as
2()
1ii
i
PR
ui PT
P
RPTPR
P
TNCus sPT
PT
is
PG
YXX
PG 

 nn
(11)
2()
1
i
i
ii
i
d
ui PTd PR PT
P
TNCus sPT
PT
is
PG
YXX
PG 

 nn
(12)
In the previous two time phases, PT and si have trans-
mitted their data respectively. And we assume that the
destination nodes PR and di know exactly the useful
messages from their source nodes, where Xu is for the PR
from PT in the first phase and i
s
X
is for di from si in
the second phase. So after they have received signals
Xi-NC in the third phase, each destination node can per-
fectly distinguish its useful signal from the combined
signals.
Thus, the PT can completely extract Xu from Xi-NC and
we can get the required signal ˆPR
P
TNC
Y
2()
1
ˆi
i
PR
ui PT
P
TP
us P
PT
is
PR
PT NC
PG R
T
X
nn
PG
Y



 (13)
And di extracts i
s
X
from Xi-NC, then we have the
needed signal ˆdi
P
TNC
Y
2()
1
ˆi
i
ii i
i
d
ui PTd PT PT
is ssPT
PT
is
di
PT NC
PG PG Xnn
PG
Y



(14)
From (13), the PU’s SINR in the third phase is
22
(3) (1 )
i
PR
PR ui PT
PT PR PT
ui PTi s
PG
PG PG



 (15)
Using (14), the SINR at node di is given by
22
(3) (1 )
i
i
i
i
d
dui PT
PT dPT
ui PTi s
PG
PG PG



 (16)
Therefore, with (3) and (15), the PU’s achievable rate
in the jth sub-channel is
2
222
log(1(1)(3)) / 3
PP
log(1)
3(1 PP)
i
jPRPR
PUPT PT
PR PR
uPTuPT
PR PT
ui PTis
RW
GG W
GG 2





(17)
As for SU i, its achievable rate is
2
2222
log(1(2)(3)) / 3
PP
log(1)
3(1 PP)
ii
iii
ii
i
i
dd C
iPT sddPT
isuPTis
dPT
ui PTi s
RW
GGPG
W
GG 





(18)
where W is the sub-channel’s bandwidth. The coefficient
1/3 dues to the fact that cooperative transmission uses
one third of the resources.
3. Problem Formulation
There are two fundamental questions on power allocation
to be addressed: 1) The incentives of PU and SUs for
using cooperative transmissions; 2) The optimal power
Pui allocated to SU i. In this section, we present a
game-theoretic framework of the transmit power alloca-
tion at the PU for the SUs.
3.1. SUs’s Utility Function
To depict a SU’s satisfaction with the received relay
power from the PT, we define a utility function for SU i as:
CC
ii
UgRP
ui

 (19)
where in the right side of the equation, the first term is
the gain and the second term is the cost by using coop-
erative transmissions. g is a positive constant providing
conversion of units, is the achievable rate in (18),
C
i
R

represents the price per unit of power charged by the
PT, and Pui denotes how much power SU i will buy from
the PT.
Each SU aims at maximizing its own utility, which
subjects to the total available transmit power Pt of the PT.
Thus, we can model the optimal cooperative power de-
mand of each SU as
max
s.t. 0PP
ui
CC
ii
P
ui t
UgR P
ui


 (20)
Clearly, the utility function is concave in Pui, so
we can solve the optimal power Pui by taking the deriva-
tive of in (19) with the respect to Pui as
C
i
U
C
i
U
0
CC
ii
ui ui
UR
g
PP




 (21)
For simplicity, we define

Q. WU ET AL. 241
2
2
2
';1
3ln(2) 1
;
i
i
ii
i
d
is
i
PT PT
is is
ii
d
PT
PG
gW
WA
PG PG
BC
G






(22)
Substituting (22) into (21), we can get the optimal co-
operative power ()
ui
P

expressed in (23) for maximiz-
ing the utility function .
C
i
U
22 2
1
() 2() 4'
()(2),
,2, ...,
ui
ii
iiiiiii iiii
PAB W
BCABCBCACBC
ii N







 



 (23)
3.2. PU’s Utility Function
The PU’s utility is based on the rate it achieves and the
gain of selling its power Pt to the SUs. Thus, the PU’s
utility function is given by
C
P
UPU
UgR t P

 (24)
where 1
M
j
P
U
j
R

PU R is the total achievable rate of
the PU in all M sub-channels, and t P

is the total pay-
ment from the SUs.
The choice of price

is important to the PU. Since
the PU can choose either to use the power itself or to
share the power with SUs. For the PU, we define the res-
ervation price of the power as the expense of relaying for
the SUs. This reservation price is also called cost, which
represents the adverse effects of SUs’ transmissions on
PU’s performance. It may consist of device depreciation,
power consumption, performance degradation of PU, etc.
We denote the reservation price of PU as 0

.
4. Power Auction Mechanism
We model a single-auctioneer, multiple-bidder power
trading market, in which the PU wants to sell and the
SUs want to buy the relay power. And we discuss how
the PU sells its power to the SUs by using an auction
mechanism. The auction procedures can be briefly de-
scribed as follows: the PT, i.e. the “auctioneer”, an-
nounces a price, the SUs, i.e. the “bidders”, report to the
auctioneer their demanded power at that price. The auc-
tioneer updates the price and the process repeats until the
total demanded power meets the maximum available
supply power of the PT.
The proposed scheme is based on the traditional as-
cending clock auction (ACA-T) [16]. As shown in Algo-
rithm 1, before the auction, the PT initially sets clock
index 0

, the step size 0

, and a reserved price
0

 . For each auction clock 0, 1,...,

 there is a
specific price


corresponds to it. The PT announces
the price to the SUs. Based on the announced price


,
each SU submits its optimal power demand ui ()P


,
which refers to (23), to the PT. After receiving all the
demands, the PT sums up all the bids
1
() ()
N
tal ui
i
PP






()
tal t
PP

and compares it with Pt. If

, the auction continues to time 1


. Then
the PT raises the price 1


 


tal T
P
and announces
the new price to all SUs. Otherwise, the auction con-
cludes and the current time denoted as T. Since the price
increases discretely, the demanded power of each SU
may decrease, and we might have t
()P

. In order
to fully utilize the power Pt (i.e. t ()
tal T
PP

), we apply
a proportional rationing rule [19] and the final allocated
power is g iv en by
*()ui
ui ui T
ui
PP 1
1
11
() (
()
ui T
NN
ui
ii
PP
PP




 1
N
i


)
()
t
T
P

()
T



T
T


ui
P  (25)
Algorithm 1 Ascending Clock Power Auction Algo-
rithm
1. Initialization
PT initializes clock index 0

, step size 0

,
gives the available power , and announces the ini-
tial price
t
P
0

with the reserve price.
Each SU i computes its optimal power demand
0
()
ui
P

, and submits the bid to PT.
PT sums up all the b() ids 00
ui
1
N
i
PP()
tal

 ,
and compares it with


t
P.
t
2. Bid Update
WHILE (()
tal 
PP


1 
)
· PT sets





, 1

 ;
· PT announces


to all the SUs;
· Each SU computes its ()
ui
P


based on (23),
and submits the best bid to PT;
· PT sums up all the bids 1
N
i
PP()
tal ()
ui





.
END
3. Power Allocation
Conclude the auction, set T


*
ui
, and according to
(25), allocate to SU i.
*
ui
P
4. Paymen t
Finally, each SU i pays to PT.
T
P 
where *
1
N
ui t
i
P
P



T
P 
0
. Consequently, the payment from
SU i to the PT is . Note that, the power constraint
in the auction is
*
ui
iuit
PP



, and we can get the op-
timal strategy for SU i, {1,2,..., }iN

as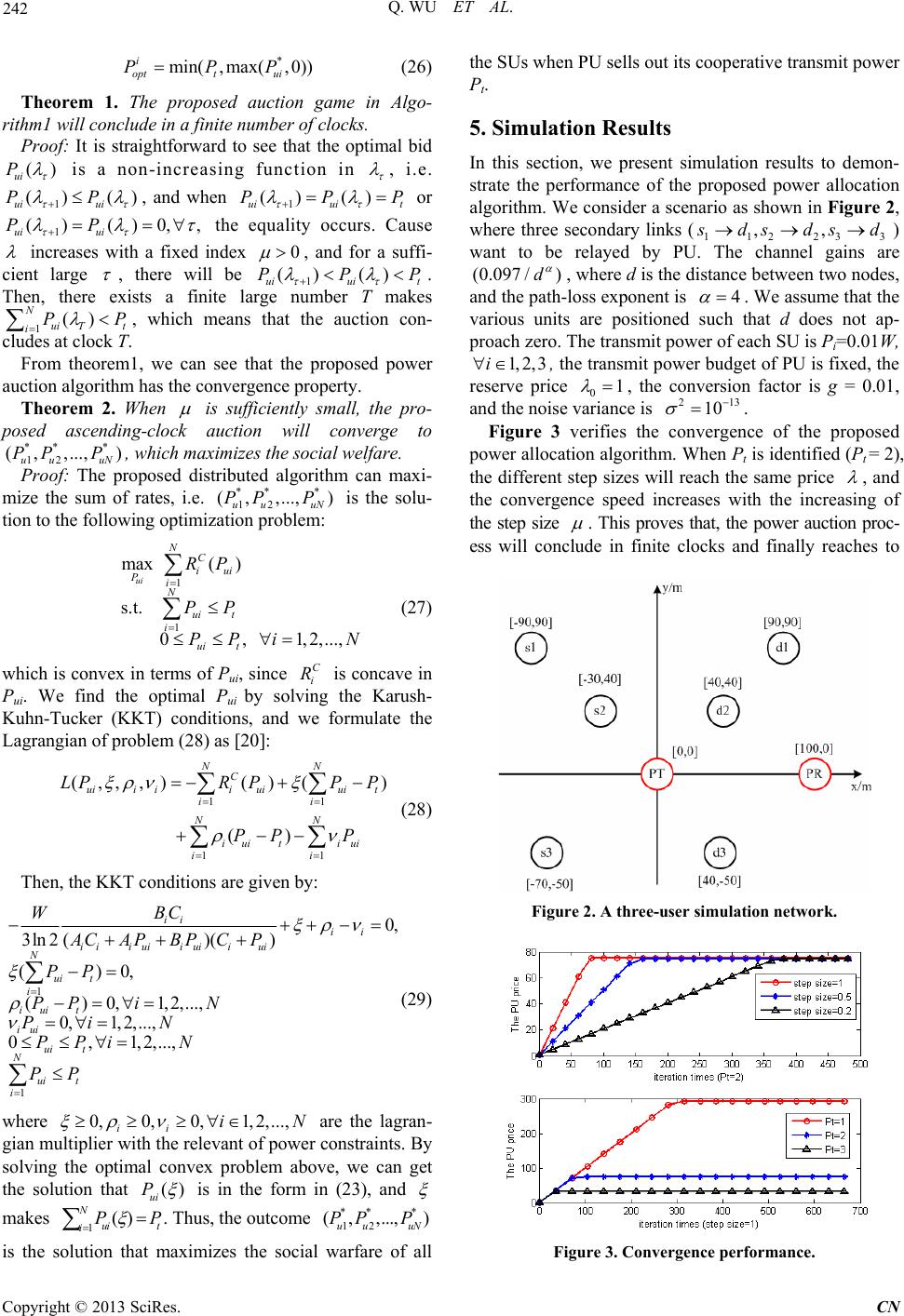

Q. WU ET AL.
242
*
min( ,max(,0))
i
optt ui
PPP (26)
Theorem 1. The proposed auction game in Algo-
rithm1 will conclude in a finite number of clocks.
Proof: It is straightforward to see that the optimal bid
()
ui
P


is a non-increasing function in


, i.e.
1
()
ui
P(
ui
P)



 
, and when 1
() (
uiui t
PP

)P


 or
1
()
ui ( ui
PP

)0,,

  
 the equality occurs. Cause

increases with a fixed index 0

, and for a suffi-
cient large

, there will be 1uit PP

() ()
ui P

 
.
Then, there exists a finite large number T makes
1i()
N
ui Tt
P
P 
, which means that the auction con-
cludes at clock T.

From theorem1, we can see that the proposed power
auction algorithm has the convergence property.
Theorem 2. When

is sufficiently small, the pro-
posed ascending-clock auction will converge to
, which maximizes the social welfare.
** *
12
( ,,...,)
uu uN
PP P
Proof: The proposed distributed algorithm can maxi-
mize the sum of rates, i.e. is the solu-
tion to the following optimization problem:
** *
12
( ,,...,)
uu uN
PP P
1
1
max( )
s.t.
0, 1,2,...,
ui
NC
iui
PiN
ui t
i
ui t
RP
PP
PP iN



 

 (27)
which is convex in terms of Pui, since is concave in
Pui. We find the optimal Pui by solving the Karush-
Kuhn-Tucker (KKT) conditions, and we formulate the
Lagrangian of problem (28) as [20]:
C
i
R
11
11
(,,,)() ()
()
NN
C
uii iiuiuit
ii
NN
iui tiui
ii
LPR PPP
PP P
 



 



(28)
Then, the KKT conditions are given by:
1
1
0,
3ln2 ()()
()0,
() 0,1,2,...,
0, 1,2,...,
0,1,2,...,
ii ii
iiiuiiui i ui
N
ui t
i
iui t
iui
ui t
N
ui t
i
BC W
ACAPBPCP
PP
PP iN
Pi N
PPi N
PP







 








N
(29)
where 0,0, 0,1,2,...,
ii i

 
()
ui
P
are the lagran-
gian multiplier with the relevant of power constraints. By
solving the optimal convex problem above, we can get
the solution that

is in the form in (23), and

makes s, the outcome ** *
12
( ,,...,)
uu uN
PPP
PU
1()
ui t
iPP


N. Thu
is the solution that maximizes the social warfare of all
the SUs when sells out its cooperative tran smit power
In this section, we present simulation results to demon-
e proposed power allocation
Pt.
5. Simulation Results
strate the performance of th
algorithm. We consider a scenario as shown in Figure 2,
where three secondary links (112 233 ,,
s
dsds d)
want to be relayed by PU. The channel gains are
(0.097 /)d

, wh ere d is the distance between two nodes,
and the path-loss ex ponent is 4

. We assume that the
various units are positioned such that d does not ap-
proach zero. The transmit power of each SU is Pi=0.01W,
1, 2,3i

, the transmit power budget of PU is fixed, the
reserve price 01


, the conversion factor is g = 0.01,
and the noise variance is 213 10 

.
Figure 3 verifies the convergence of the proposed
power allocation algorithm. When Pt is id entified (Pt = 2),
the different step sizes will reach the same price

, and
the convergence speed increases with the increasing of
the step size

. This proves that, the power auction proc-
ess will conclude in finite clocks and finally reaches to
Figure 2. A three-user simulation network.
Figure 3. Convergence performance.
C opyright © 2013 SciRes. CN

Q. WU ET AL. 243
the optimal power allocation. Fro m the below sub-fig, we
can see that with the same step size (1

), the iteration
times T decreases with the increasing of Pt. This is be-
cause that when the total relay power Pt of PT is suffi-
ciently large, and the total demanded cooperative power
by SUs is less than Pt, then the relay will sell the power
early in the auction with a relatively lower price.
Figure 4 shows the allocated power of each SU. It’s
evident that with the increase of PU’s power Pt, the co-
operative power of each SU increases, with SU 2 has the
largest power while SU 3 has the smallest. This attrib-
uted to the local in formation of th e SUs, such as lo cation,
their transmit power, the path-loss.
We furte users in
issio
the the
so
her show the rates and utilities of th
the CR network in Figure 5 and Figure 6. Figure 5
shows the rates in cooperative transmn (CT) in this
paper versus the direct transmission (DT). It is obvious
that the cooperativ e way can greatly improve the rates of
SUs. And with the relay power increases, the rates of
each SU increase slowly. The sum rates of this coopera-
tive communication can effectively maximize
cial welfare. The order of magnitude of the rates is big,
so the growth in the image is not that obvious. In Figure
6, we can see that the utilities of SUs have the same trend
with rates, which demonstrates that the auction-based
power allocation algorithm in this work can greatly im-
prove the SUs’ utilities.
6. Conclusions
In this article, we tackled the power allocation problem
for the relay-assisted SUs’ transmission, where the PU
acts as the relay and the SUs transmitting in spectrum
underlay mode. We proposed a distributively power auc-
tion algorithm, which based on the traditional ascending
clock auction (ACA-T). The convergence and social
Figure 5. The achievable rates of the SUs.
Figure 6. The utility achieved by the SUs.
welfare properties are investigated and simulated. Future
work can be extended to the case with many PUs in the
network.
7. Acknowledgements
The work has been partially supported by the NSFC
grants (No. 61271211), and the Research Program from
Shanghai Science and Technology Commission (No.
11510707000).
REFERENCES
[1] FCC, “Spectrum policy task force report ET Docket, Tech.
Rep. 02-155,” FCC, Tech. Rep., Nov. 2002.
[2] J. Mitola and G. Q. Maguire, “Cognitive Radio: Makin
Sof
mun
g
tware Radios More Personal,” IEEE Personal Com-
ications, Vol. 6, No. 4, 1999, pp. 13-18.
Figure 4. The obtained transmit power of the SUs.
C opyright © 2013 SciRes. CN

Q. WU ET AL.
244
doi:10.1109/98.788210
unications, Vol. 23, No. 2, 2005, pp. 201-220.
/JSAC.2004.839380
[3] S. Haykin, “Cognitive Radio: Brain-empowered Wireless
Communications,” IEEE Journal on Selected Areas in
Comm
doi:10.1109
V. Tarokh, “Achievable R
,” IEEE Transactions Infor-
[4] N. Devroye, P. Mitran and
in Cognitive Radio Channelsates
mation Theory, Vol. 52, No. 5, 2006, pp. 1813-1827.
doi:10.1109/TIT.2006.872971
[5] S. K. Jayaweera and M. Bkassiny, “Asymmetric Coop-
erative Communications Based Spectrum Leasing via
Auctions in Cognitive Radio Networks,” IEEE Trans.
Wireless Com11, pp. 2716-2724.
doi:10.1109/TWC.2011.061311.102044
mun., Vol. 10, No. 8, 20
cient P
[6] P. Cheng, A. Guo, Y. Xu, X. Wang and X. Gao, “A Game
Approach for Dynamic Resource Allocation in Cognitive
Radio Networks,” Wireless Communications and Signal
Processing (WCSP), 2010, pp. 1-6.
[7] J. N. Laneman, D. N. C. Tse and G. W. Wornell, “Coop-
erative Diversity in Wireless Networks: Effiroto-
cols and Outage Behavior,” IEEE Transactions Informa-
tion Theory, Vol. 50, No. 12, 2004, pp. 3062-3080.
doi:10.1109/TIT.2004.838089
[8] Y. Wu, P. A. Chou and S. Y. Kung, “Information Ex-
change in Wireless Networks with Network Coding and
Physical-layer Broadcast,” MSR-TR-2004, Vol. 78, 2005.
[9] J. Zou and H. Xu, “Auction-Based Power Allocation for
Multiuser Two-Way Relaying Networks,” IEEE Transac-
tions Wireless Communications, Vol. 12, No. 1, 2013, pp.
31-39. doi:10.1109/TWC.2012.113012.111725
[10] K. B. Letaief and W. Zhang, “Cooperative Communica-
tions for Cognitive Radio Networks,” Proceedings of the
IEEE, Vol. 97, No. 5, 2009, pp. 878-893.
doi:10.1109/JPROC.2009.2015716
[11] A. Ghasemi and E. S. Sousa, “Fundamental Limits of
Spectrum-Sharing in Fading Environments,” IEEE
Transactions Wireless Communications, Vol. 6, No. 2,
2007, pp. 649-658. doi:10.1109/TWC.2007.05447
[12] Y. Chen, G. Yu, Z. Zhang, H. hwa Chen and P. Qiu, “On
5
Cognitive Radio Networks with Opportunistic Power
Control Strategies in Fading Channels,” IEEE Transac-
tions Wireless Communications, Vol. 7, No. 7, 2008, pp.
2752-2761. doi:10.1109/TWC.2008.07014
[13] S. Stotas and A. Nallanathan, “Optimal Sensing Time and
Power Allo-cation in Multiband Cognitive Radio Net-
works,” IEEE Transactions Wireless Communications,
Vol. 59, No. 1, 2011, pp. 226-235.
doi:10.1109/TCOMM.2010.110310.090473
[14] C. Yang, J. Li and Z. Tian, “Optimal Power Control for
Cognitive Radio Networks under Coupled Interference
Constraints: A Cooperative Game-Theoretic Perspective,”
IEEE Transactions Vehicular Technology, Special Issue
on Cognitive Radio, 2010.
[15] P. Zhou, W. Yuan, W. Liu and W. Cheng, “Joint Power
and Rate Control in Cognitive Radio Networks: A
Game-Theoretical Approach,” in Proc. IEEE Interna-
tional Conference on Communications, 2008, pp.
3296-3301.
[16] Y. Chen, Y. Wu, B. Wang and K. Liu, “Spectrum Auc-
tion Games for Multimedia Streaming over Cognitive
Radio Networks,” IEEE Transactions on Communica-
tions, Vol. 58, No. 8, 2010, pp. 2381-2390.
doi:10.1109/TCOMM.2010.08.090528
[17] J. Zou, H. Xiong, D. Wang and C. W. Chen, “Optimal
Power Allocation for Hybrid Overlay/Underlay Spectrum
Sharing in Multiband Cognitive Radio Networks,” IEEE
Transactions Vehicular Technology, Vol. 62, No. 4, 2013,
pp. 1827-1837. doi:10.1109/TVT.2012.2235152
[18] S. Sharma, Y. Shi, Y. T. Hou and S. Kompella, “Is Net-
work Coding Always Good for Cooperative Communica-
tions,” IEEE INFOCOM, 2010, pp. 1-9.
[19] L. M. Ausubel, “An Efficient Ascending-bid Auction for
Multiple Objects,” American Economic Review, Vol. 94,
2004, pp. 1452-1475. doi:10.1257/0002828043052330
[20] S. Boyd and L. Vandenberghe, Convex Optimization.
Cambridge University Press, 2003.