Communications and Network, 2013, 5, 232-237
http://dx.doi.org/10.4236/cn.2013.53B043 Published Online September 2013 (http://www.scirp.org/journal/cn)
Dynamic Spectrum Access Scheme of Variable Service Rate
and Optimal Buffer-Based in Cognitive Radio
Qiang Peng1, Youchen Dong2*, Weimin Wu2, Haiyang Rao2, Gan Liu2
1Wuhan University of Technology, Wuhan, Hubei, China
2Wuhan National Laboratory for Optoelectronics, Department of Electronics and Information Engineering,
Huazhong University of Science and Technology, Wuhan, Hubei, China
Received April, 2013
ABSTRACT
Dynamic spectrum access (DSA) scheme in Cognitive Radio (CR) can solve the current problem of scarce spectrum
resource effectively, in which the unlicensed users (i.e. Second Users, SUs) can access the licensed spectrum in
opportunistic ways without interference to the licensed users (i.e. Primary Users, PUs). However, SUs have to vacate
the spectrum because of PUs coming, in this case the spectrum switch occurs, and it leads to the increasing of SUs’
delay. In this paper, we proposed a Variable Service Rate (VSR) scheme with the switch buffer as to real-time traffic
(such as VoIP, Video), in order to decrease the average switch delay of SUs and improve the other performance.
Different from previous studies, the main characteristics of our studying of VSR in this paper as follows: 1) Our study is
on the condition of real-time traffic and we establish three-dimension Markov model; 2) Using the internal optimization
strategy, including switching buffer, optimizing buffer and variable service rate; 3) As to the real-time traffic, on the
condition of meeting the Quality of Service(QoS) on dropping probability, the average switch delay is decreased as well
as improving the other performance. By extensive simulation and numerical analysis, the performance of real-time
traffic is improved greatly on the condition of ensuring its dropping probability. The result fully demonstrates the
feasibility and effectiveness of the variable service rate scheme.
Keywords: Cognitive Radio; Dynamic Spectrum Access; Variable Service Rate; Optimal Buffer; Markov Decision
1. Introduction
In recent years, with the development of wireless tech-
nology, the demand of spectrum resource increases day
by day, as a result, the competition among people to
spectrum resource becomes intense. The competition
between 3G cellular network and Wi-Fi is presented in
[1], it makes the marketing of internet broadband expand
gradually and this tendency poses a threat on the QoS.
Thereby, it is extremely urgent to solve the problem of
scarce spectrum resource. However, as we know, in
traditional static spectrum allocation scheme, most
licensed band is always under-utilization seriously, such
as presented in [2]. On the other hand, the unlicensed
band (i.e. 2.4 GHz and 5 GHz) is very crowded. In this
case, the cognitive radio network (CRN) based on spectrum
sharing, which can improve the spectrum efficiency greatly,
emerges as the times require. In CRN, the SUs are
allowed to access the licensed spectrum hole without
interference to PUs opportunistically by using dynamic
spectrum access strategies of spectrum. But when the
PUs comes, SUs has to vacate the band that it is
receiving service and then switches to other channel that
is idle. Obviously, it can increase the delay, and if there
is no idle channel being monitored, the SUs will face
forcing to terminate service, namely dropping. So these
cases, which make the performance worse, stimulated the
interest of scientists.
In recent years, many models and algorithm are pro-
posed in [3-6] to analyze the performance, including
blocking probability, dropping probability and through-
put, in Cognitive Radio Network (CRN), such as the op-
timal reserve channel model proposed in [3], the dynamic
heterogeneous spectrums Multiple Channel Reuse Areas
(MCRA) model given in [6] and some other models.
However, these authors ignored a vitally important per-
formance metric, i.e., delay of SUs. The good news is
that server papers [7-9] made up for the shortage by us-
ing different models. In [7], there were four kinds of
DSA schemes being proposed, including centralized
CRN and distributed CRN, to analyze the system per-
formance. Beside, the reserve channel and buffer also
were considered, yet, the setting of the number of buffer
is not very reasonable, which will be seen in the next
analysis. In [8], the throughput and delay were intro-
C
opyright © 2013 SciRes. CN

Q. PENG ET AL. 233
duced for cognitive radio ad hoc network (CRAHN) by-
capturing the impact of PU activity in dense and sparse
PU deployment conditions. And in [9], the hybrid proto-
col model for the SUs and a framework for general cog-
nitive network were established to study the two impor-
tant performance metrics, i.e., throughput and delay of
SUs.
In this paper, different from these studies introduced
above, we focus on the average handoff delay of SUs, as
well as the other metrics, including blocking probability,
dropping probability, throughput considering the buffer
and variable service rate. The contribution of this paper
is three-fold. First, we establish three-dimension Markov
model to improve the performance metrics on the real-
time traffic. Second, we not only consider the buffer, but
analyze the impact of variance of the number of buffer
on the throughput of SUs, and give the algorithm for the
optimal number of buffer. Third, as is stated in [10], al-
though the Trellis Coded Modulation scheme is used in
Orthogonal Frequency Division Multiple Access to in-
crease the achievable rate, the unalterable fact is that the
higher the service rate, the higher the transmission power.
Thereby, given that the trade-off between the necessary
transmitted power and the effective data rate for a given
bandwidth, the variable service rate, according to the
state information of the system, in this paper is consid-
ered.
The remainder of the paper is structured as follows. In
Section II, the system model is presented, while its
Markov-chain model and performance evaluation are
detailed in Section III, separately. In Section IV, we give
the numerical results and the conclusions in Section V.
2. System Model
2.1. Assumptions
For simply analysis, we make some assumptions, which
don’t affect our analysis, as follow:
1) There exist PUs and only one kind of SUs(i.e. video
traffic) in the system. And the traffic arrival process of
PUs and SUs are assumed to be a Poisson with a rate of
p

and
s

, separately, while the traffic holding time of
PUs and SUs are assumed to be negative exponential
associated with a mean value of 1
p

and 1
s

.
2) There are N channels in CRN, and each channel is
divided into M of the same sub-channel. Each PU occu-
pies a channel (that is M sub-channel), while each SU
only occupies a sub-channel. The buffer in CRN in our
model is a different characteristic from some other stud-
ies, and a buffer denotes a sub-channel. For simplicity,
we assume that the number of buffer () is no
less than M. This assumption is reasonable, because if
is less than M, the dropping probability of
SUs will be great because of the PUs’ coming. The sys-
tem model is showed in Figure 1.
_n buffer
_nbuffer
3) When a PU comes, if the number of PUs in CRN
are less than N, the PU will be accepted, otherwise it will
be blocked, at the same time, if the channel chosen by
PU is occupied by SUs, the SUs will monitor other idle
channel to access or stay in buffer to wait for idle chan-
nel, if there is no idle channel in buffer, the SUs will be
dropped. When a SU comes, if there is idle sub-channel,
the SU will be accepted, otherwise it will be blocked.
4) The SUs in buffer is priority to the new coming SUs.
When there is SUs in buffer, the new coming SUs will be
rejected to access.
This paper, we consider the impact of the variable
serving rate of system on performance of the system by
using a Markov chain model, which will be introduced in
part B in detail. The problem is described that the system
adjusts its serving rate according to the current channel
state information (CSI). That is when there are SUs in the
buffer, the system will increase the serving rate, and the
more the SUs in the buffer are, the faster the serving rate
is. On the other hand, we will analyzed the impact of
different number of buffer on the throughput of SUs, and
then give the optimal number of buffer to maximize the
throughput of SUs.
2.2. Markov-Chain Model
In this paper, the stochastic variables , and
denote the number of active Pus, the number of
active SUs and the number of SUs in buffer respectively
at time t, where
()
p
Nt ()
s
Nt
()
s
Bt




 

0, ,
ps
Nt NN0,t,NM and


s
B t[0, _nb]uffer . So we can derive the state vector


{,tN(),()}tBt
pss
, it denotes a state of Markov-
Chain at time t. Based on the above assumptions and
analysis, the Markov-Chain model can be depicted in
Figure 1. In Figrue 1, we use {i, j, k} replace
{
SN


,(),Nt()Bt
pss
In Figure 2, the transition from state (i, j, k) to other
state, or from other state to state (i, j, k) occur with four
possible cases, i.e., PU arrival, PU departure; SU arrival,
SU departure. And each state transition is with its corre-
sponding rate. Taking an example of SU, when a SU
arrives, the state (i, j-1, k) will be transferred to state (i, j,
k) with the transition rate 1s
, in which 1
Nt }.
σλσ1

with
the condition k = 0, otherwise . When a SU
1
σ0
Figure 1. The system model.

Q. PENG ET AL.
234
kji ,,
''''
,,1 kji 
1,,  kji kji ,1,

''
,,1 kji 
p

p
 
2
s
 
2
s
 
1
s
 
2
p

p
 
3
Figure 2. State transition of markov-chain model.
departures, the transition from state (i, j, k) to state (i, j-1,
k) or state (i, j, k-1) with transition rate , where
and .
2s
σμ
_knbuf
2
σ(1/ _)k nbuffer jj
''
3
σ(1 /)fer
'
,0kk In Figure 2, on the condition of
, and on the condition of
'

''
,jjMkk
kMM
_
M
kn buffer'
j
, as well as = j + k,
'
_
,_ )knbufferM nbuffer（
on the condition of . And the value of
and are also depend on the value of k, when k = 0,
_kn buffer'' j
''
k
'' ''
,jjnkk n
M
,1,
,
where , max(0, (1))niMjN
'' ''
else + min (_. ,jjMkk , )nbufferkM
Thereby, we set up all equilibrium equations for every
state according to these arrows described above with
eleven undetermined coefficients and (
i = 1, 2; j
= 1, 2,…, 5)
i
αj β
' ''' ''
12 ,,
12 3
1, ,1,,
4,1,5,,1
()
pspsijk
p
ps
ijk ijk
sij ksijk
ijp
ppp
pp
 

 




 

ijk
(1)
where:
1
2
1
2
3
1 ()
0
1 ()
0
1 (0)
0
1 ()
0
1 (0)
0
if iN
else
if i MjNM
else
if i
else
iifiN
else
if j
else

























4
5
1 ()
0
(_)
0
jifiMjNM
else
jifknbuffer
else











Then, combining the normalized condition (2), we can
get the steady state probability of each state.
,,
000,
1
buffer
n
NNM iM
ijk
ijkiMjNM
p



  (2)
With these steady state probabilities, we can evaluate
the performance metric of the system, i.e., blocking
probability, dropping probability, average handoff delay
and throughput rate.
3. Performance Analysis and Algorithm
Description
3.1. Performance Analysis
1) The average handoff delay of SUs: SUs, which are
being accepted service, are forced to switch to the buffer
to wait for idle channel because of the arriving PU and
no idle channel. The average time of staying in buffer is
the average handoff delay, given in [7].
handoff buffer
interference handoff
NN
Delay NR 
(3)
where
handoffsteady
handoff SS
S
NNP
,
denotes the average number of SUs which are forced to
switch to the buffer when a PU comes, in which, S de-
notes the state space and
s
teady
S
P denotes the steady state
probability under the state S.
max(0, min(_, (1)))
handoff
S
NnbufferkiMjN M,
denotes, under the state S, the number of SUs which are
forced to switch to the buffer when a PU comes.
s
teady
interferenceinterference S
S
NNP
, denotes the average number
of SUs which disturb to the new coming PU.
s
teady
buffer S
S
NkP
, denotes the average number of SUs
in the buffer.
handoff steady
handoff p
SS
S
RNP  , denotes the average rate of
switching to the buffer for SUs, i.e., the average number
of switching to the buffer per unit time.
2) The blocking probability of Sus: When all channels
are occupied, the coming SU will be blocked.
,,
,
block
s
u
SiMj NM
p

ijk p (4)
3) The dropping probability of SUs: When there are no

Q. PENG ET AL. 235
enoughchannels to accept the occupied SUs by PU, the
occupied SUs will be dropped. First, we will consider the
dropping probability of each SU:


,, max(0, 1
(_))
su
drop ijk
eachS
pp iM
jNMnbufferk

 
 
 (5)
So, to all SUs, the dropping probability is:
_
(1 )
drop
peach su
drop
su block
ssu
p
pp



 (6)
4) The throughput rate of SUs: The SUs are not
blocked and dropped.
(1)(1)
throughput drop
block
sus susu
pP   p (7)
3.2. Algorithm Description
In the previous model, the numbers of buffer are equal to
all the number of sub-channel. The only advantage of
this model is no dropping probability, because the buffer
can hold all the SUs which are occupied by PU. However,
two disadvantages are resulted: one is that there are a lot
of SUs in buffer, so the waiting time of SUs in buffer
becomes long, i.e., the average handoff delay becoming
long; the other one is that the author want to decrease the
dropping probability to improve the throughput of SUs,
but in fact, there are some SUs always stay in the buffer
because of no idle channel being monitored, so the
throughput of SUs may not be improved. In this case, we
can decrease the numbers of buffer to decrease the aver-
age handoff delay of SUs, as well as not decreasing the
throughput. However, there is a problem: how many
buffers are optimal? Next, the algorithm of computing
the optimal buffer for variable arrival rate of PUs in algo-
rithm 1 will be presented.
Algorithm 1the computing of optimal n_buffer
for 1:
p
ppn

 ;
for =1 : _n buffer*NM


_;
throughput
su
a nbufferp
end
1
_
()
p
nbuffer

{
_
|n buffermax(a[1],a[2] … a
[])}; *NM
end
1
_
[_(),,_()]
p
pn
n buffern buffern buffer

 
;
Taking an example，we give the parameters: 3,N

2,1,1.5, 0.8,0.4
pp ss
M



 
_nbuffer
, we can see the
variation of the throughput of SUs with the variable
showing in Figure 3. When ≤4,
the throughput of SUs increase with the increasing of the
number of buffer, while decrease when ≥4.
The reason is that the more the number of buffer is, the
more the average number of SUs in the buffer is, so the
less chance that the new SUs accepted will be, referring
to the assumption (4), i.e., the higher the blocking prob-
ability will be. On the other hand, although the dropping
probability decrease with the increasing number of buffer,
its value is so low that leads to the increasing of the total
throughput. According to the analysis, we can get the
optimal number of buffer is4 that can result the maximal
throughput of SUs in this case.
_n buffe
_nbuffe
r
r
4. Simulation Result
In this section, we will evaluate each of the performance
metrics analyzed above versus the variable arrival rate of
PUs by simulation result. Let the parameters be:
3,2,1.5, 0.8,0.4
ps s
NM




 ; the range of
p

is
from 0 to 1.0 and the step is 0.1. According to the de-
scription of algorithm above, we have
_
[0,2,3,3,4,4,4,4,4,4,4]n buffer


for each of
p

. For demonstrating our advantage, we
give the different simulation result for invariable service
rate (IVSR) with
_
6nbuffer

, variable service rate (VSR)
with
_
6n buffer

and variable service rate (VSR) with
_uffern _ffern bbu

, where the is a vector
with the element of optimal number of buffer for differ-
ent arrival rate of PUs.
_n buffer
Figure 4 and Figure 5 show that as expected, the av-
erage handoff delay and the blocking probability of SUs
increasewith increasing the arrival rate of PUs, because
the numbers of idle channels decrease with increasing the
traffic load of PUs, the accepted new SUs decrease and
the number of SUs staying in buffer increase. However,
as we expected, the average handoff delay and the
blocking probability of SUs in VSR scheme decreases
compared with IVSR. Furthermore, these two metrics
also decrease in VSR scheme compared the maximal
number of buffer (
_
6n buffer) and the optimal number
11.5 22.533.544.5 55.56
0.65
0.66
0.67
0.68
0.69
0.7
0.71
t he Number of Buffer
Throughput of SUs ( users / sec )
Figure 3. The throughput of SUs vs. the number of buffer.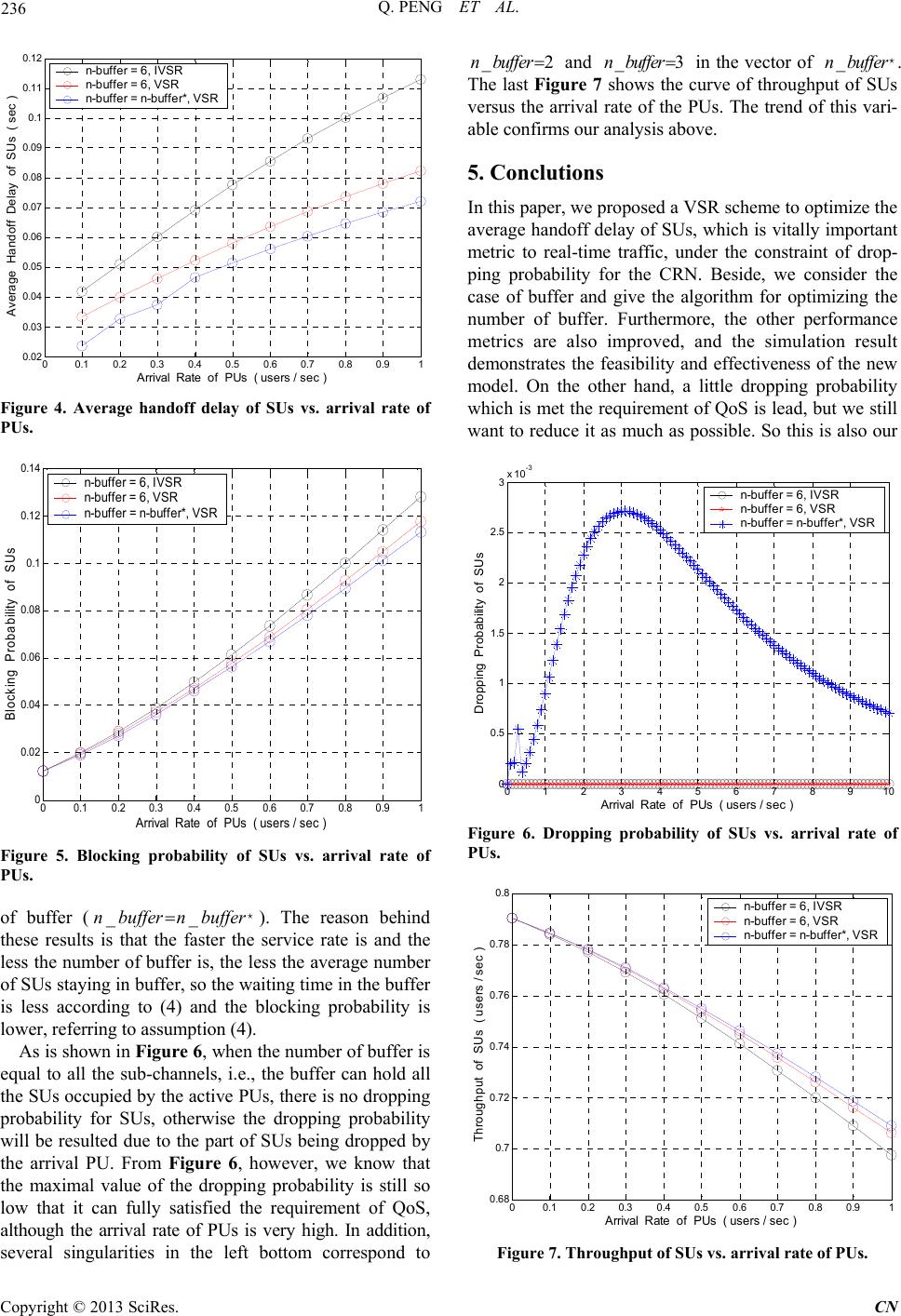

Q. PENG ET AL.
236
00.1 0.2 0.3 0.4 0.5 0.6 0.70.8 0.91
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0.11
0.12
Arrival Rate of PUs ( users / sec )
Average Handoff Delay of SUs ( sec )
n-bu ffe r = 6, IV S R
n-bu ffe r = 6, V S R
n-bu ffe r = n-buffer*, V S R
Figure 4. Average handoff delay of SUs vs. arrival rate of
PUs.
00.1 0.20.3 0.4 0.50.6 0.70.8 0.91
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
Arrival R ate of PUs ( users / sec )
Blocking Probability of SUs
n-buffer = 6, IV SR
n-buffer = 6, V S R
n-bu ffe r = n-buffe r*, V S R
Figure 5. Blocking probability of SUs vs. arrival rate of
PUs.
of buffer (). The reason behind
these results is that the faster the service rate is and the
less the number of buffer is, the less the average number
of SUs staying in buffer, so the waiting time in the buffer
is less according to (4) and the blocking probability is
lower, referring to assumption (4).
__nbuffer nbuffer
As is shown in Figure 6, when the number of buffer is
equal to all the sub-channels, i.e., the buffer can hold all
the SUs occupied by the active PUs, there is no dropping
probability for SUs, otherwise the dropping probability
will be resulted due to the part of SUs being dropped by
the arrival PU. From Figure 6, however, we know that
the maximal value of the dropping probability is still so
low that it can fully satisfied the requirement of QoS,
although the arrival rate of PUs is very high. In addition,
several singularities in the left bottom correspond to
_
2nbuffer

and
_
3nbuffer

in the vector of .
The last Figure 7 shows the curve of throughput of SUs
versus the arrival rate of the PUs. The trend of this vari-
able confirms our analysis above.
_nbuffer
5. Conclutions
In this paper, we proposed a VSR scheme to optimize the
average handoff delay of SUs, which is vitally important
metric to real-time traffic, under the constraint of drop-
ping probability for the CRN. Beside, we consider the
case of buffer and give the algorithm for optimizing the
number of buffer. Furthermore, the other performance
metrics are also improved, and the simulation result
demonstrates the feasibility and effectiveness of the new
model. On the other hand, a little dropping probability
which is met the requirement of QoS is lead, but we still
want to reduce it as much as possible. So this is also our
0 1 2 3 4 5 6 7 8 910
0
0.5
1
1.5
2
2.5
3x 10
-3
Arrival Rate of PUs ( users / sec )
Droppi n g P robab ility of SUs
n -buffer = 6, IVSR
n -buffer = 6, VSR
n -buffer = n-buffer*, V SR
Figure 6. Dropping probability of SUs vs. arrival rate of
PUs.
00.1 0.20.3 0.4 0.5 0.60.7 0.8 0.91
0.68
0.7
0.72
0.74
0.76
0.78
0.8
Ar rival R ate of PUs ( users / sec )
Throughput of SUs ( users / sec )
n -buffer = 6, IVSR
n -buffer = 6, VS R
n -buffer = n-buffer*, V SR
Figure 7. Throughput of SUs vs. arr ival rate of PUs.

Q. PENG ET AL.
237
future work.
6. Acknowledgements
This work is supported by the National Natural Science
Fund of China(No.61071068), the National High Tech-
nology Research and Development Program of China
(No. 2012AA121604), and theInternational S&T Pro-
gram of China（No.2012DFG12010).
REFERENCES
[1] W. Lehr and L. W. McKnight, “Wireless Internet access:
3Gvs.WiFi?,” Telecommun. policy, Competition Wirel.,
Spectr., Service Technol. Wars, Vol. 27, No. 5/6, 2003,
pp. 351-370.
[2] M. A. McHenry, “NSF Spectrum Occupancy Measure-
ments ProjectSummary,” Shared Spectrum Company Re-
port, Aug. 2005.
[3] X. Zhu, L. Shen and T. P. Yum, “Analysis of Cognitive
Radio Spectrum Access with Optimal Channel Reserva-
tion,” IEEE Communications Letters, Vol. 11, No. 4, pp.
304-306, Apr. 2007. doi:10.1109/LCOM.2007.348282
[4] G. Liu, X. Zhu and L. Hanzo, “Dynamic Spectrum Shar-
ing Models for Cognitive Radio Aided Ad Hoc Networks
and Their Performance Analysis,” Proceeding of IEEE
GLOBECOM 2011.
[5] E. W. M. Wong and C. H. Foh, “Analysis of Cognitive
Radio Spectrum Access with Finite User Polulation,”
IEEE Communications Letters, Vol. 13, No. 5, 2009, pp.
294-296. doi:10.1109/LCOMM.2009.082113
[6] G. Liu, X. Zhu and L. Hanzo, “Impact of Variance of
Heterogeneous Spectrum on Performance of Cognitive
Radio Ad Hoc Network,” IEEE ICC, Vol. 1, No. 1, Jun
2012.
[7] Tumuluru, V.K.;Ping Wang; Niyato, D.and Wei Song,
“Performance Analysis of Cognitive Radio Spectrum
Access With Prioritized Traffic,” IEEE Transactions on
Vehicular Technology, Vol. 61, No. 4, 2012, pp.
1895-1906. doi:10.1109/TVT.2012.2186471
[8] P. Zhou, Y. S. Chang and John A. Copeland, “Capacity
and Delay Scaling in Cognitive Radio AdHoc Networks:
Impact of Primary User Activity,” IEEE Globecom, 2010.
[9] W. T. Huang and X. B. Wang, “Throughput and Delay
Scaling of General Cognitive Networks,” IEEE Infocom,
2011.
[10] N. Mokari, H. Saeedi and KeivanNavaie, “Channel Cod-
ing Increases the Achievable Rate of the Cognitive Net-
works,” IEEE Communications Letters, Vol. 17, No. 3,
March 2013, pp. 495-498.