Communications and Network, 2013, 5, 223-231
http://dx.doi.org/10.4236/cn.2013.53B2042 Published Online September 2013 (http://www.scirp.org/journal/cn)
A New Genetic Algorithm Applied to Multi-Objectives
Optimal of Upgrading Infrastructure in NGWN
Dac-Nhuong Le1, Nhu Gia Nguyen2, Dac Binh Ha2, Vinh Trong Le3
1Faculty of Information Technology, Haiphong University, Haiphong, Vietnam
2Duytan University, Danang, Vietnam
3Hanoi University of Science, Vietnam National Universi ty, Hanoi, Vietnam
Received June, 2013
ABSTRACT
A problem of upgrading to the Next Generation Wireless Network (NGWN) is backward compatibility with
pre-existing networks, the cost and operational benefit of gradually enhancing networks, by replacing, upgrading and
installing new wireless network infrastructure elements that can accommodate both voice and data demand. In this pa-
per, we propose a new genetic algorithm has double population to solve Multi-Objectives Op timal of Upgrading Infra-
structure (MOOUI) problem in NGWN. We modeling network topology for MOOUI problem has two levels in which
mobile users are sources and both base stations and base station controllers are concentrators. Our objective function is
the sources to concentrators connectivity cost as well as the cost of the installation, connection, replacement, and capac-
ity upgrade of infrastructure equipment. We generate two populations satisfy constraints and combine them to build
solutions and evaluate th e performance of my algorithm with data randomly generated. Numerical results show that our
algorithm is a promising approach to solve this problem.
Keywords: Multi-Objectives Optimal; Next Generation Wireless Network; Network Design; Capacity Planning;
Genetic Algorithm; Two-populations
1. Introduction
The Next Generation Wireless Networks (NGWNs) are
expected to provide high data rate and optimized quality
of service to multimedia and real-time applications over
the Internet Protocol networks to anybody, anywhere,
and anytime. The wir eless netw ork infrastructure con sists
of equipment required by mobile network operators to
enable mobile telephony calls or to connect fix
subscribers by radio technology. The interacting layers
architecture of next generation wireless network is shown
in Figure 1.
The PSTN-cloud covers all network elements to make
a standard telephone call, while the data network cloud
includes the Internet, Intranets, and other IP based net-
works [1]. The architectural building blocks enabling
mobile telephony are:
 The core network: comprised of the mobile
switching centers (MSC), the packet data serving
nodes (PDSN), and home agents (HA), and
 The base station subsystem (BSS) also known as
the radio access network, consisting of base sta-
tion controllers (BSC), base transceiver stations
(BS), and mobile stations (MS).
Figure 1. The NGWN infrastructure.
C
opyright © 2013 SciRes. CN

D.-N. LE ET AL.
224
Corresponding to the architectural building blocks of a
wireless network, are three types of interconnects [2].
These are (1) mobile device to BS interconnect, which
includes both forward and reverse radio links, (2) the BS
to BSC interconnect, which is called the backhaul, and (3)
BSC to MSC interconnect. The known hierarchical ca-
pacitated concentrator location problem, which is an ex-
tension of the concentrator location problem to multiple
levels and a classical research issue in the telecommuni-
cations literature [3-6]. In [7], the authors studied the
base station location an d service assignment prob lem in a
W-CDMA. A greedy strategy to optimal positioning of
BSs for cellular radio networks and capacity planning of
UMTS networks studied in [8-9]. A Tabu search and
Genetic algorithm approach to cellular capacity expan-
sion to maximizing the coverage area and minimizing the
number of transmitters is presented in [10,11]. Yu et al in
[12] proposed a set covering algorithm for given traffic
and finding optimal solution configuration in a CDMA
network. An alternate approach to capacity planning and
expansion is introduced for 3G network system capacity
without an increase in BSs using a cell splitting app roach
[13].
In latest papers [14-18], we have proposed a novel
Particle Swarm Optimization (PSO), Ant Colony Opti-
mization (ACO) and Genetic algorithms (GA) to optimal
location of controllers in wireless networks and cen-
tralized wireless access network. In this paper, we focus
on the Multi-Objectives Optimal of Upgrading Infra-
structure (MOOUI) in NGWN and propose a new Ge-
netic algorithm to solve it. The rest of this paper is or-
ganized as follows: Section 2 presents the MOOUI prob-
lem formulation. Section 3 presents our new algorithm to
solve it based on GA algorithm. Section 4 is our simula-
tion and analysis resu lts, and finally, section 5 concludes
the paper.
2. Problemformulation
In this section, we assume that network topology has m
mobile users, n base stations, and p base station controllers.
we introduce the following notation in Table 1 below.
The MOOUI problem in NGWN has two steps the ini-
tial assignment of MSs to BS and the connection of BS to
BSC and capacity expansion and traffic increase with
constraint specifies that:
 Each mobile user MSi will be assigned to exactly
one base station BSj of type t
 Mobile usersare within that base stations’ maxi-
mum ran ge _
M
axBSCov
 At most one base station of type t can exist at lo-
cation j
 if a base station BSj is operated, it has to be con-
nected to a BSCk and the BSC has to be active.
Table 1. Notation defininition.
Notation Meaning
M Index set of Mobile user locations:


,1..
i
M
MS im
N
Index set of all Base Station (BS):


12, 1..
j
NN NBS jn 
N1: Index set of exi sting BS;
N2: Index set of potential BS
P
Index set of Base Station Controllers (BSC):


12, 1..
k
P
PP BSCkp 
P1: Index set of exis ting BSC;
P2: Index set of potential BSC
Tj Set of types available for , j
B
SjN
S
Set of commodity types:
1if commonditytypeisvoice
2if commonditytypeisdata
s 

t
N Index set of all BS of type t. 12
tt t
N
NN
s
i
D
Demand of commodity type s for mobile user
,
i
M
SiM
_t
j
M
axBS CapMaximum capacity of
j
BS of type t, t
j
N .
_k
M
axBSC CapMaximum capacity of ,
k
B
SCk P
t
ij
d Distance of mobile user i
M
Sfrom j
B
Sof type
t ,t iMjN 
_t
j
M
axBS CovMaximum coverage range for j
B
Sof type t
cost_connect t
j
kCost of connecting j
B
Sof type t to
k
BSC
cost_installk Cost of installing ,2
k
BSCk P
cost_upgradej Per channel cost of upgrading ,1
j
B
SjN
cost_setup t
j
Cost of constructing and connecting,2
j
BSj N
The capacity constraints of the model, in which we
argue that BSs must have the necessary capacity to ac-
commodate traffic demand of all demand types s for all
MSs assigned to it and the BSC must have the necessary
capacity to accommodate all BSs assigned to it.
In the first step, we use the indicator variables are:
1ifoftype isoperated
0otherwise
t
j
j
BS t



 (1)
1ifof typeisconnectedto
0otherwise
t
j
k
jk
BS tBSC



 (2)
1ifis operatedininitialassigment
0otherwise
k
k
BSC



 (3)
Figure 2 shows an example of an existing initial as-
signment that each mobile user can be assigned to only
one BS, while each BS has to be connected to a single
BSC.

D.-N. LE ET AL. 225
Figure 2. The indicator variables in Initial Assignment step.
In the second step, we use the decision variables are:
1if mobileuseris connectedto
0otherwise
t
i
ij j
M
SB
X 

S
(4)
1ifof typeis connectedto
0otherwise
t
j
k
jk
BS tBSC
Y 
 (5)
1ifof typeis operated
0otherwise
t
j
j
BS t
Z 
 (6)
1ifis operated
0otherwise
k
k
BSC
W 
 (7)
Figure 3 illustrates an assignment after capacity ex-
pansion and traffic increase, and indicates the respective
decision variables. New wireless BSS infrastructure
equipped with BS and BSC in red shades.
The objective of MOOUI is to minimize the total cost
of expanding an initial wireless BSS to accommodate
increased traffic demand.
The MOOUI problem can be defined as follows:



2
1
2
11
( cost_connect
cost_install
cost_upgrade _
cost_setup )
tt t
j
tt
j
tt
j
p n
jk jkjk
jktT
kk k
kP
jjj
jN tT
jj
jNtT
Min Y
W
MaxBS capZ
Z















 



jt
(8)
Subject to:
1
1, 1..
t
j
n
ij
jtT
X
im


 (9)
,1..,1..,
ttt
ij ijjjj
dXMaxCovZimjnt T
(10)
1, 1..
t
j
j
tT
Z
j



1
,1..,
tt
p
j
jk j
k
Z
Yjnt

T

 
 (12)
,1..,1.. ,
t
j
kk j
YWkpj ntT (13)

2
11
_,1..,
ttt
ms
iijj jj
is
D
XMaxBSCapZjntT


 
 (14)
1
_
,1.
t
j
n
jkk k
jtT
YMaxBSC CapWkp


 .
(15)






0,1 ,0,1 ,0,1 ,0,1
1..,1.. ,1..,
tt t
ijj kjk
j
XYZW
imjnk ptT

 (16)
3. A New Genetic Algorithm for the MOOUI
3.1. Represent and Decode an Individual
In this section, we present a new genetic algorithm for
the MOOUI problem with two populations X and
Y. The encoding of the configuration is by
means of matrix
POP
POP X POP
m
()
ij n
Xx


, where
xij = 1 means that mobile user MSi has been connected to
base station BSj, and other wise, xij=0. The encoding of
the POPY configuration is by means of matrix
(1..,1inj..)m
(), (1..,1..)
jk mp
Yyjmkp

,
where yjk = 1 means that base station BSj has been con-
nected to base station controller BSCk, and other wise, yjk
= 0.
3.2. Initialization
We use fully random initialization in order to initialize
the individuals X ensure that the individual x satis-
fies constraints in (9)(10)(14) and (16). Each individual x,
we fully random initialization in order to initialize the
individuals Y ensure that the individual y satisfies
constraints in (12)(13)(15) and (16).
POP
POP
Figure 3. The assignment after capacity expansion and
traffic increase with decision variables.
n
(11)

D.-N. LE ET AL.
226
3.3. Crossover Operator
This operator minics the mating process in the nature. To
do crossover in X, two individuals are picked first
and two integer numbers(i,j)(crossover point is xij) are
generated randomly between [1,n] and [1,m] (where nis
number of MSs and m is number of BSs).
POP
Then the offspring is generated by interchanging the
second halves of its parent, as illustrated in Figure 4.
In the crossover stage, the algorithm examines all pairs
of individuals. It begins with the pairs that include the
individual with a higher fitn ess value until the p opulation
size becomes twice of the original size. Similar, we apply
crossover operator to .
Y
POP
3.4. Mutation Operator
The mutation operation is one kind of random change in
the individual of X. In our algorithm, point wise
mutation is adopted, in which one gene in the individual
is changed with a certain probability, referred to as the
mutation probability. This operator allows the algorithm
to search for new and more feasible individuals in new
corners of the solution spaces.
POP
To do mutation, an individual is randomly selected
from the BS and the selected BS is called the mutation
point, as illustrated in Figure 5.
10 11110 111 1
20 21220 212 2
01 01
00 000 0
Parent
j m
j m
ij ij im im
ii ii
nm nm
nn nnn n
xx xxx x x
xx xxx x x
xx
xx xx xx
xx
xx xxx x
 













 






 



 



1011110 111
1
2021220212 22
01 01
000000
s
j
m
jj mm
ij ij im im
ii ii
nm nm
NNNnnn
xxxxxx
1
2
j
m
j
m
x
x














1
j
m
x
x
xxxxxx xx
xx
x
x
xx xx
x
x xxxxx x




 


 







 






  

 
 
 


Childrent





















2
j
m
x
x
x








 


Figure 4. The crossover operator for population POPx.
10 11110 111
11
20 21220212
2
01 01
00 0000
Parents
jj
mm
j
m
ij ij im im
ii ii
nm nm
nn nnnn
xx xxxx xx
xx xxxx
x
xr xr
x xx xx
x xx xxxx


















 


  
 
Childrent






Figure 5. The mutation operator for population POPx.
The mutation stage is implemented until eith er popula-
tion size becomes twice of the original size or all indi-
viduals in the current generation are examined. Similar,
we apply mutation operator to .
Y
POP
3.5. Evaluation Function
After the mutation, each solution




,| ,
XY
s
x yxPOPyPOP
is satisfies constraints in (9)-(16). The cost function of
solution s computed by formula (8).
3.6. Our GA Algorithm Proposed
The pseudo-code of our algorithm as follows:
A NEW GENETIC ALGORITHM FOR THE MOOUI
BEGIN
INITIALISE populationX
P
OP withrandomcandidatesolutions;
REPEAT
1. SELECT parents in X
P
OP ;
2. RECOMBINE pairsofparents in X
P
OP ;
X
P
OP 3. CROSSOVER the resultingoffspring in ;
4. MUTATION the resultingoffspring in X
P
OP ;
X
x
POP
5. FOR each eachcandidateDO
5.1 INITIALISE populationY
P
OP withrandomcandidate
solutions Y yPOP

x
follows candidateX POP

;
5.2. SE LECT parents inY
P
OP ;
Y
P
OP 5.3. RECOMBINE pairsofparents in ;
5.4. CROSSOVER the resultingoffspring in Y
P
OP ;
Y
P
OP 5.5. MUTATION the resultingoffspring in ;
5.6. COMBINE Solution




,| ,
XY
s
x yxPOPyPOP
6. EVALUATE FUNCTION newsolutions s by formula (8);
7. SELECT individualsxfor the nextgeneration;
UNTIL (TERMINATION CONDICTION issatisfied)
END
4. Experiments and Results
4.1. The Problems Tackled
In our experiments, we have tackled several MOOUI
instances of different difficulty levels. There are 10
MOOUI instances with values for M, N and P is shown
in Table 2.
4.2. Parametersfor the GA Algorithm
In our experiments, we have already defined our cross-
over probability as 0.7, we will work with a population
size of 500 and a mutation ra te of 1
m
pm.
Our GA algorithm to tackle these problems can be
specified as below in Table 3.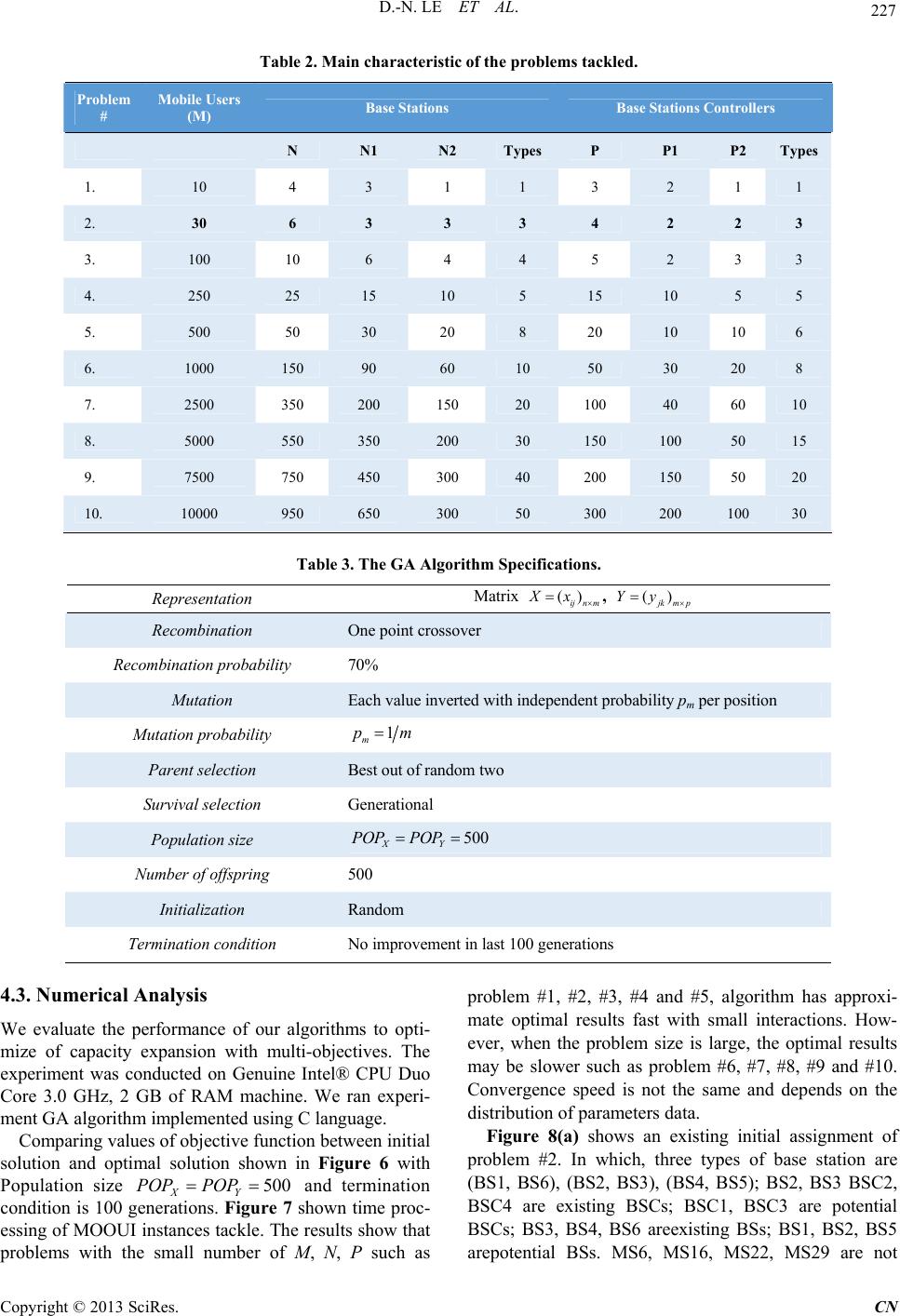

D.-N. LE ET AL.
227
Table 2. Main characteristic of the problems tackled.
Problem
# Mobile Users (M) Base Stat i ons Base Stat i ons Cont r ol ler s
N N1 N2 Types P P1 P2 Types
1. 10 4 3 1 1 3 2 1 1
2. 30 6 3 3 3 4 2 2 3
3. 100 10 6 4 4 5 2 3 3
4. 250 25 15 10 5 15 10 5 5
5. 500 50 30 20 8 20 10 10 6
6. 1000 150 90 60 10 50 30 20 8
7. 2500 350 200 150 20 100 40 60 10
8. 5000 550 350 200 30 150 100 50 15
9. 7500 750 450 300 40 200 150 50 20
10. 10000 950 650 300 50 300 200 100 30
Table 3. The GA Algorithm Specifications.
Representation Matrix ()
ijnm
Xx

, ()
jkmp
Yy 
Recombination One point crossover
Recombination probability 70%
Mutation Each value inverted with independent probability pm per position
Mutation probability 1
m
pm

Parent selection Best out of random two
Survival selection Generational
Population size 500
XY
POP POP


Number of offspring 500
Initialization Random
Termination condition No improvement in last 100 generations
4.3. Numerical Analysis problem #1, #2, #3, #4 and #5, algorithm has approxi-
mate optimal results fast with small interactions. How-
ever, when the problem size is large, the optimal results
may be slower such as problem #6, #7, #8, #9 and #10.
Convergence speed is not the same and depends on the
distribution of parameters data.
We evaluate the performance of our algorithms to opti-
mize of capacity expansion with multi-objectives. The
experiment was conducted on Genuine Intel® CPU Duo
Core 3.0 GHz, 2 GB of RAM machine. We ran experi-
ment GA algorithm implemented using C language. Figure 8(a) shows an existing initial assignment of
problem #2. In which, three types of base station are
(BS1, BS6), (BS2, BS3), (BS4, BS5); BS2, BS3 BSC2,
BSC4 are existing BSCs; BSC1, BSC3 are potential
BSCs; BS3, BS4, BS6 areexisting BSs; BS1, BS2, BS5
arepotential BSs. MS6, MS16, MS22, MS29 are not
Comparing values of objective function between initial
solution and optimal solution shown in Figure 6 with
Population size and termination
condition is 100 generations. Figure 7 shown time proc-
essing of MOOUI instances tackle. The results show that
problems with the small number of M, N, P such as
500
XY
POP POP

D.-N. LE ET AL.
228
connected. Figure 8(b) shows an optimal solution with
BSC2 is replaced by BSC3, BS4 is replaced by BS2 and
BS5. BS1 is added and connect to BSC4. Red edges are
replace connections and black edges are existing connec-
tions.
To evaluation the effect of population size and number
of iterations to the value of the objective function. We
consider the problem #2 with the iterations can vary from
100 to 500 and fixed population size is 500, comparing
results are shown in Figures 9(a) and (b). To comparing
the problem #2 with the population size can vary from
500 to 1000 and fixed iterations size is 100, comparing
results are shown in Figures 10(a) and (b). The experi-
mental results show that the algorithm can be imple-
mented with the big number of interactions and large
population size in polynomial time. From this result, we
confirmed that this is a promising approach to solve this
problem.
Figure 6. Comparing value of capacity expansion in the MOOUI instances tackle.
Figure 7. Time processing MOOUI instances tackle.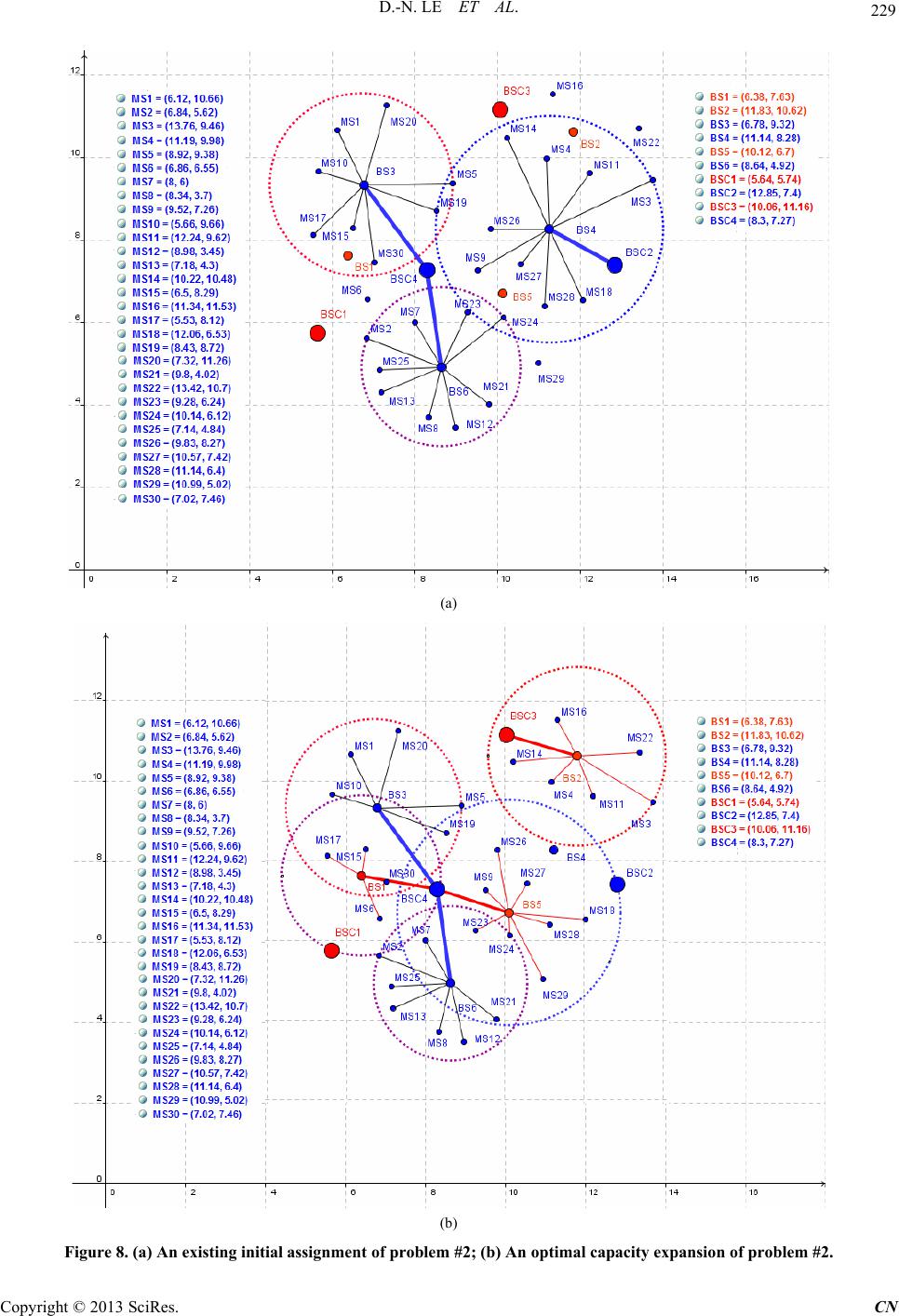

D.-N. LE ET AL. 229
(a)
(b)
Figure 8. (a) An existing initial assignment of problem #2; (b) An optimal capacity expansion of problem #2.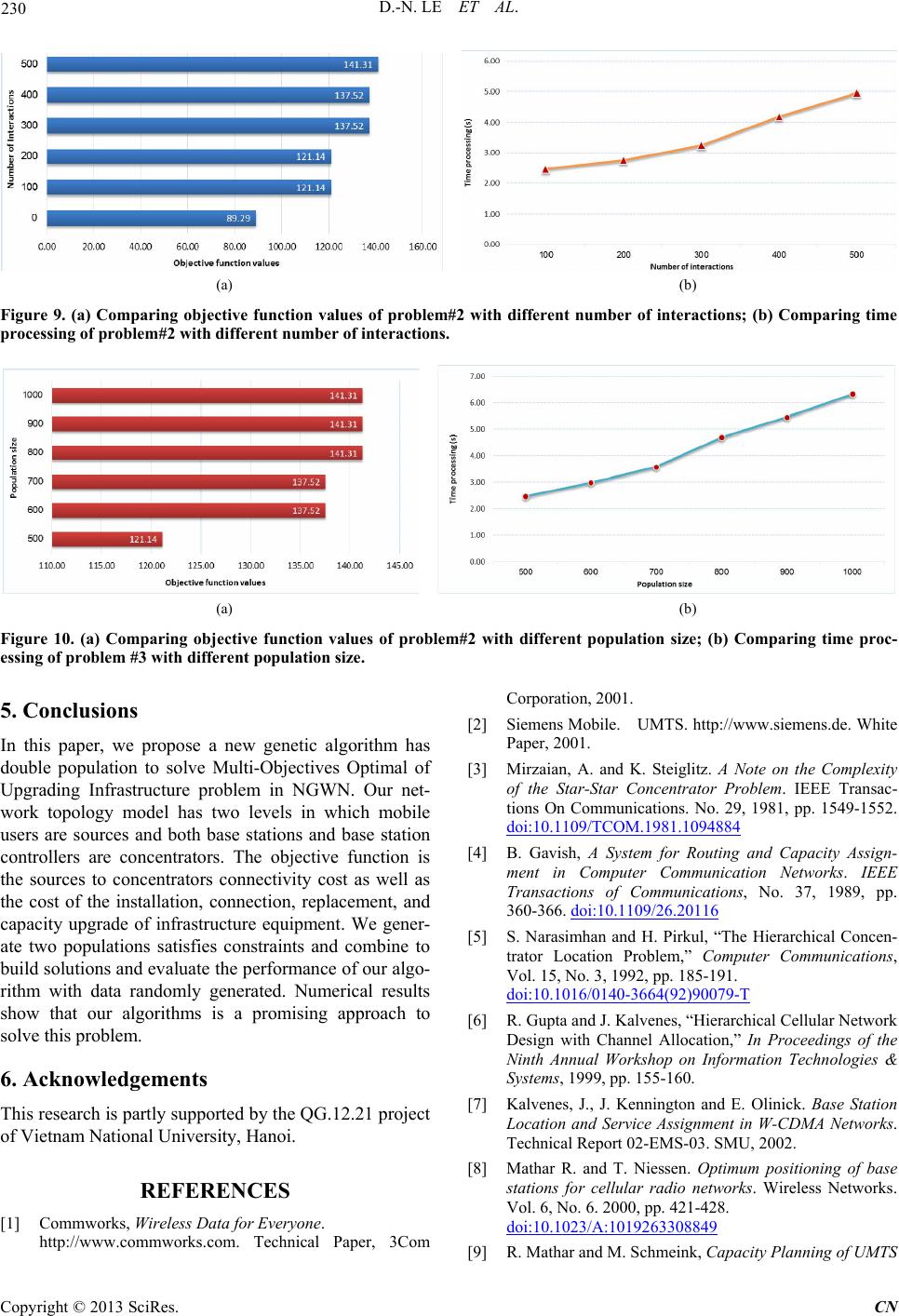

D.-N. LE ET AL.
230
(a) (b)
Figure 9. (a) Comparing objective function values of problem#2 with different number of interactions; (b) Comparing time
processing of problem#2 with different number of interactions.
(a) (b)
Figure 10. (a) Comparing objective function values of problem#2 with different population size; (b) Comparing time proc-
essing of problem #3 with different population size.
5. Conclusions
In this paper, we propose a new genetic algorithm has
double population to solve Multi-Objectives Optimal of
Upgrading Infrastructure problem in NGWN. Our net-
work topology model has two levels in which mobile
users are sources and both base stations and base station
controllers are concentrators. The objective function is
the sources to concentrators connectivity cost as well as
the cost of the installation, connection, replacement, and
capacity upgrade of infrastructure equipment. We gener-
ate two populations satisfies constraints and combine to
build solutions and evaluate the performance of our algo-
rithm with data randomly generated. Numerical results
show that our algorithms is a promising approach to
solve this problem.
6. Acknowledgements
This research is partly supported by the QG.12.21 project
of Vietnam National University, Hanoi.
REFERENCES
[1] Commworks, Wireless Data for Everyone.
http://www.commworks.com. Technical Paper, 3Com
Corporation, 2001.
[2] Siemens Mobile. UMTS. http://www. siemens.de. White
Paper, 2001.
[3] Mirzaian, A. and K. Steiglitz. A Note on the Complexity
of the Star-Star Concentrator Problem. IEEE Transac-
tions On Communications. No. 29, 1981, pp. 1549-1552.
doi:10.1109/TCOM.1981.1094884
[4] B. Gavish, A System for Routing and Capacity Assign-
ment in Computer Communication Networks. IEEE
Transactions of Communications, No. 37, 1989, pp.
360-366. doi:10.1109/26.20116
[5] S. Narasimhan and H. Pirkul, “The Hierarchical Concen-
trator Location Problem,” Computer Communications,
Vol. 15, No. 3, 1992, pp. 185-191.
doi:10.1016/0140-3664(92)90079-T
[6] R. Gupta and J. Kalvenes, “Hierarchical Cellular Network
Design with Channel Allocation,” In Proceedings of the
Ninth Annual Workshop on Information Technologies &
Systems, 1999, pp. 155-160.
[7] Kalvenes, J., J. Kennington and E. Olinick. Base Station
Location and Service Assignment in W-CDMA Networks.
Technical Report 02-EMS-03. SMU, 2002.
[8] Mathar R. and T. Niessen. Optimum positioning of base
stations for cellular radio networks. Wireless Networks.
Vol. 6, No. 6. 2000, pp. 421-428.
doi:10.1023/A:1019263308849
[9] R. Mathar and M. Schmeink, Capacity Planning of UMTS

D.-N. LE ET AL. 231
Networks. In Proceedings of Sixth INFORMS Telecom-
munications Conference, Boca Raton, Florida 2002.
[10] C. Y. Lee and H. Kang, “Cell Planning with Capacity
Expansion in Mobile Communications: A Tabu Search
Approach,” IEEE Transactions on Vehicular Technology,
Vol. 49, No. 5. 2000, pp. 1678-1691.
doi:10.1109/25.892573/
[11] P. Calegari, F. Guidee, P. Kuonen and D. Wagner, “Ge-
netic Approach to Radio Network Optimization for Mo-
bile Systems,” IEEE VTC, pp. 755-759, 1997.
[12] C. Yu, S. Subramanian and N. Jain, “CDMA cell site
optimization using a set covering algorithm,” In Pro-
ceedings of Eight Int. Network Planning Symposium,
1998, pp. 75-78.
[13] R. Giuliano, F. Mazzenga and F. Vatalaro, “Smart cell
sectorization for third generation CDMA systems,” Wire-
less Communications and Mobile Computing, Vol. 2, No.
3, 2002, pp. 253-267.
[14] Dac-Nhuong Le, “Genetic Algorithm Applied to the Op-
timal Centralized Wireless Access Network,” Interna-
tional Journal of Information & Network Security (IJINS),
Vol. 2, No. 2, 2013, pp. 129-137.
[15] Dac-Nhuong Le and Nhu Gia Nguyen, “A New Evolu-
tionary Approach for Gateway Placement in Wireless
Mesh Networks,” International Journal of Computer
Networks and Wireless Communications (IJCNWC), Vol.
2, No. 5, 2012, pp. 550-555.
[16] Dac-Nhuong Le, “PSO and ACO Algorithms Applied to
optimal Resource Allocation to Support QoS Require-
ments in Next Generation Networks,” International Jour-
nal of Information & Network Security (IJINS), Vol. 2,
No. 3, 2013, pp. 216-228.
[17] Dac-Nhuong Le, “PSO and ACO Algorithms Applied to
Optimizing Location of Controllers in Wireless Net-
works,” International Journal of Computer Science and
Telecommunications (IJCST), Vol. 3, No. 10, 2012, pp.
1-7.
[18] Dac-Nhuong Le, “Optimizing the cMTS to Improve
Quality of Service in Next Generation Networks based on
ACO Algorithm,” International Journal of Computer
Network and Information Security (IJCNIS), Vol. 5, No. 4,
2013, pp. 25-30. doi:10.5815/ijcnis.2013.04.04
[19] Dac-Nhuong Le, “EA and ACO Algorithms Applied to
Optimizing Location of Controllers in Wireless Net-
works,” International Journal of Network Communica-
tion and Networking (IJNCN), Vol. 3, No. 2, 2013, pp.
17-27.
[20] Dac-Nhuong Le, Nhu Gia Nguyen and Vinh Trong Le,
“A Novel Ant Colony Optimization-based Algorithm for
the Optimal Centralized Wireless Access Network,” Lec-
ture Notes of the Institute for Computer Sciences, Social
Informatics and Telecommunications Engineering
(LNICST), Springer 2013.