 Journal of Computer and Communications, 2013, 1, 1-8 http://dx.doi.org/10.4236/jcc.2013.15001 Published Online October 2013 (http://www.scirp.org/journal/jcc) Copyright © 2013 SciRes. JCC Improving Personal Product Recommendatio n via Friendships’ Expansion Chunxia Yin, Tao Chu The First Aircraft Institute, Aviation Industry Corporation of China, Xi’an, China. Email: dingdong1104@163.com Received July 2013 ABSTRACT The trust as a social relationship captures similarity of tastes or interests in perspective. However, the existent trust in- formation is usually very sparse, which may suppress the accuracy of our personal product recommendation algorithm via a listening and trust preference network. Based on this thinking, we experiment the typical trust inference methods to find out the most excellent friend-recommending index which is used to expand the current trust network. Experi- mental results demonstrate the expanded friendships via superposed random walk can indeed improve the accuracy of our perso na l product re c ommendation. Keywords: Personal Product Recommendation; Trust Inference; Listening and Trust Preference Network 1. Introduction Nowadays some web sites, su ch as last.fm and delicious, have taken the lead in guiding users to build trust rela- tionships, that is, a user on such a website can select some other users with similar tastes as his/her trusted friends. The effectiveness of a recommendation algo- rithm rests with the effective use of personal information from net users. Personal trust information obviously contains reliable personal friend relations and therefore has the potential to help provide better recommendations. Based on this thinking, we proposed the LTPN algorithm [1], namely the artist recommendation algorithm via the listening and trust preference network. However, the provided user-trusted friend relations by web users are only a small fraction of the potential pairings between users so that the existent trust data is very sparse. The trust as a social relationship captures similarity of tastes or interests in perspective. Obviously, it may be difficult to know tastes or interests of a person from his sparse friendships. Instinctively, if the friendships can be accurately inferred, the sparse problem may be relieved so that the expanded friendships are expected to improve the accuracy of our LTPN algorithm. That is, th e sparsity of trust data may severely influence the behavior of our LTPN algorithm. In a word, if trust is used to support decision making, it is important to have an accurate es- timate of trust when it is not directly av ailable, as w ell as a measure of confidence in that estimate [2]. Many biological, technological, social systems can be well described by complex networks with nodes repre- senting individuals or items and links denoting the rela- tions or interactions between nodes [3-6]. As part of the surge of research on complex networks, a considerable amount of attention has been devoted to the computa- tional analysis of social networks [7]. An important scientific issue relevant to social network analysis is per - sonal trust inference, which aims at estimating the like- lihood of existence of trust with respect to a particular topic between two individuals. A number of algorithms for computing trust from social networks rely on the knowledge of the network topology, which are the main- streaming class of trust inference algorithms. They pro- vide us an entry of inferring friendships for online web users. In this paper, we investigate the use of trust inference for improving personal product recommendation. To this end, we review and discuss typical trust inference me- thods to find out the most effective friendship-expanding method, and then explore whether the expanded user- trusted friend relations can improve the accuracy of the LTPN algorithm. The numerical results indicate that the inferred friendships via superposed random walk can improve our existent trust-aware product recommenda- tion. 2. Method In this paper, we still discuss the artist as the special product. We assume that a music artist recommendation system consists of a user-set U = {u1, u2, …, un} and an artist-set A = {a1, a2, …, am}. Each user has listened to  Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC some artists and selected some other users with similar musical tastes as his/her trusted friends . The user -listened artist and user-trusted friend relations can uniformly be described by a listening and trust relation network (LTRN for short), G (U, A, E1, E2), where E1 is the set of user-trusted friend relations and E2 is the set of user- listened artist relations. Note that multiple links and self-connections are not allowed in the network. Clearly, G (U, A, E1, E2) can seen as a combination of the trust network G (U, E1) and bipartite network G (U, A, E2). Figure 1 gives a simple example of the listening and trust relation network. Each black solid line represents a listening count for a [user, artist] pair. For example, u1 has listened to a1 80 times. The red dashed curves show the mutual (undirected) trust relation s between use rs. The listening and trust relation network (a) can be seen as a combination of the trust network (b) and the bipartite network (c). To improve our LTPN algorithm, we need solve two problems. First, the personal trust between two individu- als without a direct connection needs to be inferred. We will solve this problem by applying an excellent personal trust in ference metho d to the existen t tru st network. Af ter these inferred trust relations with maximal evaluated values are added to LTRN, the expanded listening and trust relation network (ELTRN for short) will be built. Second, ELTRN is transformed into the listening and trust preference network. Obviously, ELTRN is a special LTRN. For convenience, the process of transforming the listening and trust relation network into the listening and trust preference network is called as the LTRN-LTPN transformation. We use the LTRN-LTPN transformation method in Ref. [1] to solve the second problem. Based on the above analysis, we put forward the im- proved LTPN algorithm via friendships’ expansion (FELTPN for short). FELTPN is described as the following four steps: (1) Expand the user-trusted friend relations by making use of an excellent trust inference method. (2) Build the listening and trust preference network by applying the LTRN-LTPN transformation to ELTRN. (3) Apply the LTPN algorithm to the listening and trust preference network for the personal artist recom- mendation. Next, our LTRN-LTPN transformation and LTPN al- gorithm are shortly introduced. Readers are encouraged to see Ref. [1] for their details. The u ser-listened artist relations can be expressed by a listening count matrix, Cn×m, where Cif is the listening count of ui to af. The user-trusted friend relations can be expressed by an adjacent matrix Tn×n. If there exists a mutual trust between ui and uj, Tij = Tji = 1, otherwise Tij = Tji = 0. The LTRN-LTPN transformation is as follows: (1) Transform the user-listened artist relations into the impartial listening preferences, C'n×m, in which C'if = Cif/∑gCig. (1) (2) Take advantage of the cosine similarity between the listening preferences of users to build trust prefe- rences, Ťn×n, in which 22 , if1 0 otherwise ij ij ij CC T CC ′′ ⋅ = ′′ ∗ (2) Figure 1. (Color online) A simple listening and trust relation network consisting of four users and eight artists. artists 100 60 350 40 80 210 30 100 70 50 80 61 320 20 u 3 u 1 u 2 u 4 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 230 users u 3 u 1 u 2 u 4 100 60 350 40 80 210 30 100 70 50 80 61 320 20 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 230 =+ ab c u 3 u 1 u 2 u 4 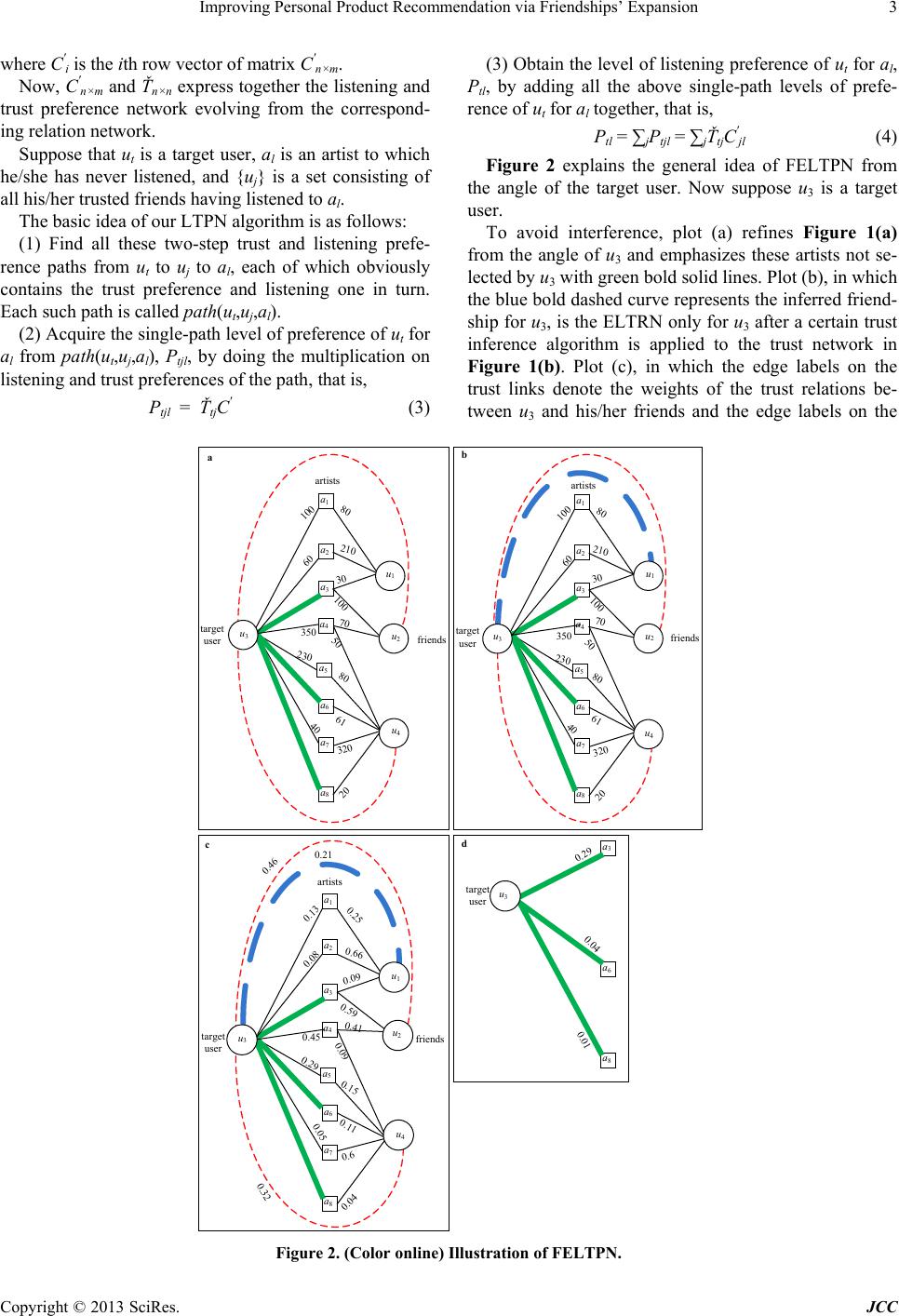 Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC where C'i is the ith row vector of matrix C'n×m. Now, C'n×m and Ťn×n express together the listening and trust preference network evolving from the correspond- ing relation network. Suppose that ut is a target user, al is an artist to which he/she has never listened, and {uj} is a set consisting of all his/her trusted friends having listened to al. The basic idea of our LTPN algorithm is as follows: (1) Find all these two-step trust and listening prefe- rence paths from ut to uj to al, each of which obviously contains the trust preference and listening one in turn. Each such path is called path(ut,uj,al). (2) Acquire the single-path level of preference of ut for al from path(ut,uj,al), Ptjl, by doing the multiplication on listening and trust preferences of the path, that is, Ptjl = ŤtjC' (3) (3) Obtain the level of listening preference of ut for al, Ptl, by adding all the above single-path levels of prefe- rence of ut for al together, that is, Ptl = ∑jPtjl = ∑jŤtjC'jl (4) Figure 2 explains the general idea of FELTPN from the angle of the target user. Now suppose u3 is a target user. To avoid interference, plot (a) refines Figure 1(a) from the angle of u3 and emphasizes these artists not se- lected by u3 with green bold solid lines. Plot (b), in which the blue bold dashed curve represents the inferred friend- ship for u3, is the ELTRN only for u3 after a certain trust inference algorithm is applied to the trust network in Figure 1(b). Plot (c), in which the edge labels on the trust links denote the weights of the trust relations be- tween u3 and his/her friends and the edge labels on the Figure 2. (Color online) Illustration of FELTPN. target user artists friends 100 60 350 40 80 210 30 100 70 50 80 61 320 20 a1 a2 a3 a5 a6 a7 a8 230 a target user artists friends 0.13 0.08 0.45 0.05 0.25 0.66 0.09 0.59 0.41 0.09 0.15 0.11 0.6 0.04 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 0.29 0.21 0.32 0.46 ca 3 a 6 a 8 d 0.29 0.04 0.01 target user artists friends 100 60 350 40 80 210 30 100 70 50 80 61 320 20 a 1 a 2 a 3 a 4 a 5 a 6 a 7 a 8 230 b u 1 a 4 u 3 u 1 u 4 u 3 u 2 u 3 u 4 u 2 u 3 u 2 u 1 u 4 target user  Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC user-listening artist links of u3 represent the levels of listening preference of u3 for the artists, presents the lis- tening and trust preference network only for u3 after the LTRN_LTPN transformation is applied to the ELTRN in plot (b). Eventually, t he pr edict ed sco res for u3 are shown in plot (d) after our LTPN algorithm is applied to the listening and trust preference network in plot (c). 3. Experiment Data and Evaluation Metrics We use a benchmark data set, lastfm, to evaluate the ef- fectiveness of the personal trust inference method and artist recommendation algorithm. The lastfm data, re- leased in the framework of HetRec 2011 (http://ir.ii.uam.es/hetrec2011), consists of 1892 users and 17632 artists from Last.fm online music system (http://www.last.fm). It records user-trusted friend and user-listened artist relations. For the purpose of effec- tively testing our algorithm, we remove those users hav- ing listened to less than ten artists. As a result, th e listen- ing and trust relation network, originating from a random sampling of 990 users, contains 49191 user-listened artist relations and 3878 mutual trust relations. Therefore, the average number of friend relations per user is 7.8 and the average number of user-listened artist relations per user is 49.69. Figure 3, where Nd is the number of users with d friends, exhibits the degree distribution of trust network from the lastfm data. Obviously, it satisfies heavy-tailed distribution, which means most users own sparse friend- ships. The personal trust inference method need calculate the likelihood of existence of all non-observed tru st relations of the target user, then sorts them in a descending order according to their likelihoods and finally recommend the target user these top-L en friends. To determine how ac- curately a personal trust inference method is able to mine Figure 3. The degree di stribution of trust network from the lastfm data. friendships, the observed user-trusted friend relations E1 need to be randomly divided into two parts: The training set Figure 3. E1Tr contains 90% of user-trusted friend relations from each user, and the remaining 10% constitutes the probe set E1Pr. E1Tr is treated as known information, while no information in E1Pr is used for prediction. Similarly, the personal artist recommendation algo- rithm need calculate the listened likelihood of all non- listened artists of the target user in the future, then sorts them in a descending order according to their likelihoods and finally recommend the target user these top-Len art- ists. To determine the effectiveness of our artist recom- mendation algorithm, user-listened artist relations E2 also need to be randomly divided into two parts: The training set E2Tr contains 90% of user-listened artist rela- tions from each user, and the remaining 10% constitutes the probe set E2Pr. E2Tr and (observed and expanded) mutual trust relations are treated as known information, while no information in E2Pr is used for prediction. We use three standard metrics, area under the receiver operating characteristic curve (AUC) [8], Precision [9] and Recall [9], to quantify the accuracy of a personal trust inference method. Note that the AUC evaluates the whole ranking list of all candidate friends while both Precision and Recall only focus on the top-Len candidate friends of the list. We use precision, recall, inter-diversity [10], intra- diversity [11] and popu larity [10] to evaluate the quality of an artist recommendation algorithm. The first two are different accuracy metrics. The inter-diversity (De) mea- sures the personalization of recommendations for differ - ent users with diff erent habits and tas tes. The intradiver- sity (Da) surveys the diversity of topics in a recommen- dation list. The last one measures the capability of recom- mendin g da rk (less pop ular) arti s t s . Before introducing concrete definitions of the above metrics, we must interpret some symbols to be used in these definitions. Denote by Ωi the set containing all n − 1 possible trust relations of ui. Then the set of all evaluated trust relatio ns of ui is where denotes the training set of trust relations of ui. Accordingly, is the probe set of trust relations of ui. Here, trust relations of ui can be interpreted as his/her trusted friends. As a matter of convenience, the (friend or artist) rec- ommendation list for ui is consistently expressed as Li and the (friend or artists) probe set for ui is consistently expressed as Pi. | · | denotes the number of elements in a set or list. The number of users having listened to af is expressed as df. Bn×m is an adjacency matrix. If ui has listened to af, Bif = 1, otherwise Bif = 0. In the present case, the AUC statistic can be inter- 0 20 40 010 2030 40 50 Degree d Nd 60 60 70 80 100 120 140 160 180  Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC preted as the probability that a randomly chosen trust relation in E1Pr is given a higher trust score than a ran- domly chosen nonexistent relation. Given the whole ranking list of all evaluated trust relations of ui, among w independent comparisons, if there are w′ times the rela- tion in having a higher score and w′′ times being of the same score, the AUC value for ui is computed as follows: AUCi = (w′ + 0.5w′′)/w. (5) The AUC for the whole system is the average over all users, that is, AUC = ∑AUCi/n. (6) The degree to which the AUC value exceeds 0.5 indi- cates how much better predictions are than pure chance. Precision is defined as the ratio of the number of rele- vant items to the total number of recommended items. Given the top-Len items of a ranking list for ui, the preci- sion for ui obviously equals |Li∩Pi|/Len. Therefore the precision of the whole system is 1 ii i PrecisionL P n Len = ∩ × ∑ . (7) Clearly, a higher value of precision means a better performance. Recall is defined as the ratio of the number of relevant items to the total number of items in the probe set. Given the top-Len items of a ranking list for ui, the recall for ui obviously equals |Li∩Pi|/|Pi|. Therefore the recall of the whole system is . (8) A higher value of recall means a better performance. A basic De measures the diversity of artists between two recommendation lists. De between two recommenda- tion lists can be quantified by the Hamming distance between the two lists. Therefore th e inter-diversity of the whole system is ( ) 21 1 ij e ij LL Dn nLen ≠ ∩ = − − ∑ . (9) Generally speaking, the greater value of De means the more personalized recommendations for different users. A basic Da measures the diversity of artists within a recommendation list. Therefore, the intra-diversity of the whole system is ( ) 12 11 afg i fg ii DS nLL ≠ = − − ∑∑ , (10) where Sfg denote s the cosine similarity betw een af and ag, namely, . (11) Generally speaking, the higher value of Da means the more diversified topics within recommendatio n lists. The popularity of a recommendation list is defined as the average degree of artists in the list. Therefore the popularity of the whole system is 11 fif i aL i Popularity d nL ∈ = ∑∑ . (12) The smaller Popularity, corresponding to the stronger capability of mining dark artists, is preferred since those lower-degree artists are hard to be found by users them- selves. 4. The Inference of User-Trusted Friend Relations In this section, we seek the most excellent (accurate and fast) trust inference method among the most influential and representative sixteen trust inference indices. These indices can be clas sified into three catego ries: local , quasi- local and global in accordance with the scope of topo- logical information used by the inference measure. Clearly, a local measure only requires the information about node degree and the nearest neighborhood, and a global measure asks for the global knowledge of network topology. Note that the quasi-local measure [12] consid- ers more topological information than the local but does not require global topological information. The refore , the global is the most time-consuming, the quasi-local takes second place, and the local needs the minimum time. We compare the accuracies of sixteen indices, which are CN [13,14], Jacard [15], Salton [16], LHN [17], HPI [18], HDI [10], Sørensen [19], PA [20], AA [21], RA [22], LP [22], LRW [23], SRW [23], Katz [24], MF I [25] and RW R [26], about predicting friends in Table 1. CN, Table 1. Accuracies of the sixteen trust inference indices when Len = 10. friend inference indices AUC Precision Recall CN 0.8353 0.014 0.6797 HDI 0.8288 0.0126 0.668 Srensen 0.8292 0.0126 0.67 PA 0.7919 0.0029 0.6289 AA 0.8375 0.0147 0.6848 RA 0.8362 0.0137 0.6794 LP ( = 0.001) 0.6662 0.0021 0.6314 RWR (c = 0.9) 0.9702 0.049 0.8318 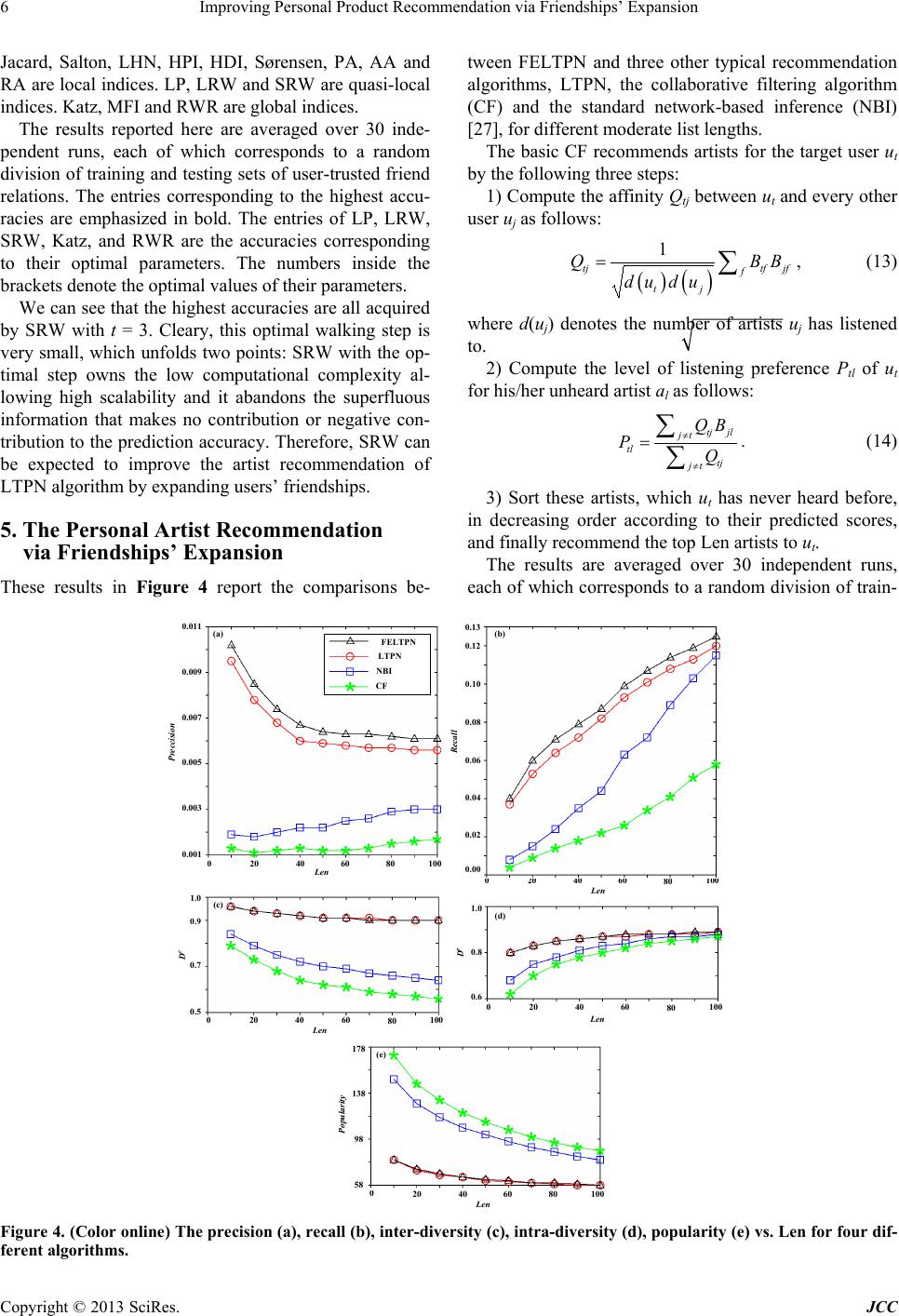 Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC Jacard, Salton, LHN, HPI, HDI, Sørensen, PA, AA and RA are local indices. LP, LRW and SRW are quasi-local indices. Katz, MFI and RWR are global indices. The results reported here are averaged over 30 inde- pendent runs, each of which corresponds to a random division of training and testing sets of user -trusted friend relations. The entries corresponding to the highest accu- racies are emphasized in bold. The entries of LP, LRW, SRW, Katz, and RWR are the accuracies corresponding to their optimal parameters. The numbers inside the brackets denote the optimal values of their parameters. We can see that the highest accuracies are all acquired by SRW with t = 3. Cleary, this optimal walking step is very small, w hich unfolds two points: SRW with the op- timal step owns the low computational complexity al- lowing high scalability and it abandons the superfluous information that makes no contribution or negative con- tribution to the prediction accuracy. Therefore, SRW can be expected to improve the artist recommendation of LTPN algorithm by expanding users’ friendships. 5. The Personal Artist Re com mendation via Friendships’ Expansion These results in Figure 4 report the comparisons be- tween FELTPN and three other typical recommendation algorithms, LTPN, the collaborative filtering algorithm (CF) and the standard network-based inference (NBI) [27], for different moderate list lengths. The basic CF recommends artists for the target user ut by the following three steps: 1) Co mpute the affinity Qtj between ut and every other user uj as follows: ( ) ( ) 1 =∑ tjtf jf f tj Q BB du du , (13) where d(uj) denotes the number of artists uj has listened to. 2) Compute the level of listening preference Ptl of ut for his/her unheard artist al as follows: . (14) 3) Sort these artists, which ut has never heard before, in decreasing order according to their predicted scores, and finally recommend the top Len artists to ut. The results are averaged over 30 independent runs, each of which corresponds to a random division of train- Figure 4. (Color online) The precision (a), recall (b), inter-diversity (c), intra-diversity (d), popularity (e) vs. Len for four dif- ferent algorithms. LTPN NBI CF FELTPN 0.001 0.003 0.005 0.007 0.009 0.011 02040 60 80 100 Len 0.00 0.02 0.04 0.06 0.08 0.10 02040 60 80 100 Len Preccision Recall 0.12 58 98 138 02040 60 80 100 Len Popularity 178 0.5 0.7 0.9 1.0 020 40 60 80 100 Len D e 0.6 0.8 1.0 020 40 6080 100 Len D a 0.13 (a) (b) (c) (d) (e)  Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC ing and testing sets of user-listened artist r elations. Here, ELTRN are produced by the following friendship-ex- panding method: only when the number of friends of a user is less than 10, his friendships are expanded via SRW and the number of expanded friends is set to 1. We can see from Figure 4 that the expanded friendships via SRW can improve both precision and recall of our LTPN algorithm while both outstanding diversity and excellent popularity are maintained. 6. Conclusion and Discussion In this paper, we exploit SRW to expand the personal friendships and then make use of our LTPN algorithm to recommend personal artists. The experimental results show that the expanded friendships via SRW can im- prove the recommendation accuracy of our LTPN algo- rithm. However, we can also see that the improvement is not large. External information, such as tag information and rating information, may provide more useful infor- mation and insights for personal recommendation. Fur- thermore, the sparsity of existent data and the huge size of real systems are two most main difficulties for the studies of personal recommendation. The former may result in large difficulties in building statistical models. The latter requires highly efficient algorithms because any highly accurate algorithm will become meaningless if the consuming time is unacceptable. Therefore, de- signing a better algorithm in both accuracy and speed is our future challenge, especially for sparse and huge net- works. 7. Acknowledgements The authors thank the anonymous referees for helpful suggestions and comments and acknowledge HetRec 2011 for providi n g us the lastfm data. REFERENCES [1] C. X. Yin and T. Chu, “Personal Artist Recommendation via a Listening and Trust Preference Network,” Physica A, Vol. 391, No. 5, 2012, pp. 1991-1999. http://dx.doi.org/10.1016/j.physa.2011.11.054 [2] J. Golbeck, “Trust on the World Wide Web: A Survey,” Foundations and Trends in Web Science, Vol. 1, No. 2, 2006, pp. 131-197. http://dx.doi.org/10.1561/1800000006 [3] R. Albert and A.-L. Barabasi, “Statistical Mechanics of Complex Networks,” Review s of Modern Physics, Vol. 74, No. 1, 2002, pp. 47-97. http://dx.doi.org/10.1103/RevModPhys.74.47 [4] S. N. Dorogovtsev and J. F. F. Mendes, “Evolution of Networks,” Advances in Physics, Vol. 51, No. 4, 2002, pp. 1079-1187. http://dx.doi.org/10.1080/00018730110112519 [5] S. Boccalet ti, V. Latora, Y. Moreno, M. Chavez and D.-U. Hwang, “Complex Networks: Structure and Dynamics,” Physics Report s, Vol. 424, No. 4, 2006, pp. 175-308. http://dx.doi.org/10.1016/j.physrep.2005.10.009 [6] L. da F. Costa, F. A. Rodrigues, G. Travieso and P. R. U. Boas, “Characterization of Complex Networks: A Survey of Measurements,” Advances in Physics, Vol. 56, No. 1, 2007, pp. 167-242. http://dx.doi.org/10.1080/00018730601170527 [7] D. Liben-Nowell and J. Kleinberg, “The Link-Prediction Problem for Social Networks,” Journal of the American Society for Information Science and Technology, Vol. 58, No. 7, 2007, pp. 1019-1031. http://dx.doi.org/10.1002/asi.20591 [8] J. A. Hanely and B. J. McNeil, “The Meaning and Use of the Area under a Receiver Operating Characteristic (ROC) Curve,” Radiology, Vol. 143, 1982, pp. 29-36. [9] J. L. Herlocker, J. A. Konstan, L. G. Terveen and J. T. Riedl, “Evaluating Collaborative Filtering Recommender Sys tems,” ACM Transactions on Information Systems, Vol. 22, No. 1, 2004, pp. 5-53. http://dx.doi.org/10.1145/963770.963772 [10] A. Broder, R. Kumar, F. Maghoul, P. Raghavan, S. Ra- jagopalan, R. Stata, A. Tomkins and J. Wiener, “Graph Structure in the Web,” Computer Networks, Vol. 33, No. 1, 2000, pp. 309-320. http://dx.doi.org/10.1016/S1389-1286(00)00083-9 [11] J. A. Konstan, B. N. Miller, D. Maltz, J. L. Herlocke r, L. R. Gordon and J. Riedl, “GroupLens: Applying Collabor- ative Filtering to Usenet News,” Communications of the ACM, Vol. 40, No. 3, 1997, pp. 77-87. http://dx.doi.org/10.1145/245108.245126 [12] L. Lü and T. Zhou, “Link Prediction in Complex Net- works: A Survey,” Physica A, Vol. 390, No. 6, 2011, pp. 1150-1170. http://dx.doi.org/10.1016/j.physa.2010.11.027 [13] G. Kossinets, “Effects of Missing Data in Social Net- works,” Social Networks, Vol. 28, No. 3, 2006, pp. 247- 268. http://dx.doi.org/10.1016/j.socnet.2005.07.002 [14] M. E. J. Newman, “Clustering and Preferential Attach- ment in Growing Networks,” Physical Review E, Vol. 64, No. 2, 2001, pp. 1-13. http://dx.doi.org/10.1103/PhysRevE.64.025102 [15] P. Jaccard, “Étude Comparative de la Distribution Florale Dans Une Portion desAlpes et des Jura,” Bulletin de la Societe Vaudoise des Science Naturelles, Vol. 37, 1901, pp. 547-579. [16] G. Salton and M. J. McGill, “Introduction to Modern Information Retrieval,” MuGraw-Hill, Auckland, 1983. [17] E. A. Leicht, P. Holme and M. E. J. Newman, “Vertex Si- milarity in Networks,” Physical Review E, Vol. 73, No. 2, 2006. http://dx.doi.org/10.1103/PhysRevE.73.026120 [18] E. Ravasz, A. L. Somera, D. A. Mongru, Z. N. Oltvai and A.-L. Barabási, “Hierarchical Organization of Modularity in Metabolic Networks,” Science, Vol. 297, No. 5586, 2002, pp. 1551-1555. http://dx.doi.org/10.1126/science.1073374 [19] T. Sørensen, “A Method of Establishing Groups of Equal Amplitude in Plant Sociology Based on Similarity of Spe- cies Content and Its Application to Analyses of the Vege-  Improving Personal Product Recommendation via Friendships’ Expansion Copyright © 2013 SciRes. JCC tation on Danish Commons,” Biological Skr, Vol. 5, No. 4, 1948, pp. 1-34. [20] A.-L. Barabási and R. Albert, “Emergence of Scaling in Random Networks,” Science, Vol. 286, No. 5439, 1999, pp. 509-512. http://dx.doi.org/10.1126/science.286.5439.509 [21] L. A. Adamic and E. Adar, “Friends and Neighbors on the Web,” Social Networks, Vol. 25, No. 3, 2003, pp. 211- 230. http://dx.doi.org/10.1016/S0378-8733(03)00009-1 [22] T. Zhou, L. Lü and Y.-C. Zhang, “Predicting Missing Links via Local Information,” European Physical Journal B, Vol. 71, No. 4, 2009, pp. 623-630. http://dx.doi.org/10.1140/epjb/e2009-00335-8 [23] W. Liu and L. Lü, “Link Prediction Based on Local Ran- dom Walk,” EPL, Vol. 89, No. 5, 2010. http://dx.doi.org/10.1209/0295-5075/89/58007 [24] L. Katz, “A New Status Index Derived from Sociometric Analysis,” Psychmetrika, Vol. 18, No. 1, 1953, pp. 39-43. http://dx.doi.org/10.1007/BF02289026 [25] P. Chebotarev and E. V. Shamis, “The Mat rix-Forest The- orem and Measuring Relations in Small Social Groups,” Automation and Remote Control, Vol. 58, No. 9, 1997, pp. 1505-1514. [26] S. Zhou and R. J. Mondragón, “Accurately Modeling the Internet Topology,” Physical Review E, Vol. 70, No. 6, 2004. http://dx.doi.org/10.1103/PhysRevE.70.066108 [27] T. Zhou, J. Ren, M. Medo and Y.C. Zhang, “Bipartite Network Projection and Personal Recommendation,” Phy - sical Review E , Vol. 76, No. 4, 2007. http://dx.doi.org/10.1103/PhysRevE.76.046115
|