 Applied Mathematics, 2013, 4, 1595-1598 Published Online December 2013 (http://www.scirp.org/journal/am) http://dx.doi.org/10.4236/am.2013.412215 Open Access AM Traveling Wave Solutions and Kind Wave Excitations for the (2 + 1)-Dimensional Dissipative Zabolotskaya-Khokhlov Equation Xiajie Liu, Chunliang Mei, Songhua Ma College of Science, Lishui University, Lishui, China Email: msh6209@aliyun.com Received October 1, 2013; revised November 1, 2013; accepted November 8, 2013 Copyright © 2013 Xiajie Liu et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. ABSTRACT In this work, with the help of the symbolic computation system Maple and the Riccati mapping approach and a linear variable separation approach, a new family of traveling wave solutions of the (2 + 1)-dimensional dissipative Zabolot- skaya-Khokhlov equation (DZK) is derived. Based on the derived solitary wave solution, some novel kind wave excita- tions are investigated. Keywords: Mapping Approach; Dissipative Zabolotskaya-Khokhlov Equation; Traveling Wave Solution; Kind Wave Excitation 1. Introduction In nonlinear science, soliton theory plays an essential role and has been applied in almost all the natural sci- ences, especially in all the physical branches such as fluid physics, condensed matter, biophysics, plasma phy- sics, nonlinear optics, quantum field theory, and particle physics, etc. [1-5]. How to find exact solutions of non- linear partial differential equations (PDEs) plays an im- portant role in the research of nonlinear physical phe- nomena. So it is always an interesting topic to search for meaningful solutions for PDEs. In order to find some new exact solutions, a wealth of effective methods have been set up, for instance, the bilinear method, the stan- dard Painlevé truncated expansion, the method of “coa- lescence of eigenvalue” or “wavenumbers”, the homo- genous balance method, the homotopy-perturbation me- thod, the hyperbolic function method, the Jacobian ellip- tic method, the (G’/G)-expansion method, the variable separation method, and the mapping equation method [6-15], etc. Among these methods, the mapping equation approach is one of the most effectively straightforward algebraic methods to construct exact solutions of NPDE [16-19]. In this paper, via the Riccati mapping equation we find some new exact solutions of the (2 + 1)-dimen- sional dissipative Zabolotskaya-Khokhlov equation (DZK). Based on the derived solution, we obtain some kind wave excitations of the equation. 2. New Traveling Wave Solutions of the DZK Equation The (2 + 1)-dimensional dissipative Zabolotskaya-Khok- hlov equation is 20 xtxxx xxxyy UUUUU U (1) In Ref. [20], some new exact solutions and time soli- tons have been discussed by (G’/G)-expansion method. As is well known, to search for the solitary wave solu- tions for a nonlinear physical model, we can apply dif- ferent approaches. One of the most efficient methods of finding soliton excitations of a physical model is the so-called mapping approach. The basic ideal of the algo- rithm is as follows. For a given nonlinear partial differ- ential equation (NPDE) with the independent variables 012 ,,, , m xtxx x and the dependent variable u, in the form ,, ,,0, ij txixx Puu uu (2) where P is in general a polynomial function of its argu- ments, and the subscripts denote the partial derivatives, the solution can be assumed to be in the form  X. J. LIU ET AL. 1596 0 ni i i uAq (3) with 2, (4) where σ is a constant and the prime denotes the different- tiation with respect to q. To determine U explicitly, one may substitute (3) and (4) into the given NPDE and col- lect coefficients of polynomials of Φ, then eliminate each coefficient to derive a set of partial differential equations of , i and q, and solve the system of partial differential equations to obtain , i and q. Finally, as (4) is known to possess the solutions tanh, 0, coth, 0, tan ,0, cot ,0, 1, q q q q q 0 , (5) Substituting , i q and (5) into (3), one obtains the ex- act solutions to the given NPDE. Now we apply the mapping approach to (1). By the balancing procedure, the ansatz (3) becomes 01 UAAq (6) with ,qlxmynt (7) where 0, 1, l, m, n are arbitrary constants. Substituting (6), (7) and (4) into (1) and collecting coefficients of polynomials of , then setting each coefficient to zero, we have 2 0 2 ln ,2 m 1 A l l (8) Based on the solutions of (4), one thus obtains follow- ing exact solutions of Equation (1): 2 12 3 2 ln 2tanh ,0 m Ul llxmynt l (9) 2 22 3 2 ln 2coth ,0 m Ul llxmynt l 2 32 3 2 ln 2tan ,0 m Ul llxmynt l , (11) 2 42 3 2 ln 2cot 0, m Ul llxmynt l (12) 22 52 32 3 2 ln 2,0. lnx lmnytmlx Ulxmynt l my mntl lxmynt l 2 3. Kind Wave Excitations of DZK Equation In the following discussion, we merel wave excitations of DZK equation. According to the so- lution (13) y analyze kind 210 ,U 10,lm when we set the parameters 10, 10,10n at time , we can t 0t obtain a kind wave excitation of the physical quantity 2 U presented in Figure 1. Furthermore, According to the solution 2,U when we set the parame ers 20, 20, 20lmn and 10 es a) 6t at tim , b) 3t , c) 0t , d) 3t , e) 6t , we can obtain the time evolution of a kind wave presented in Figure 2. From Figure 2, one fin ect ge wie. ensional dissipa- tive Zabolotskaya-Khokhlov equation. Based on the de- ds that the kind wave moves in the same dirion and the amplitude, velocity, and wave shape of the kind wave do not undergo any chanth tim 4. Summary and Discussion In summary, with the help of a Riccati mapping method and a linear variable separation method, we find some new exact solutions of the (2 + 1)-dim , (10) Figure 1. Plot of the kind wave structure for the physical quantity 2 U. Open Access AM 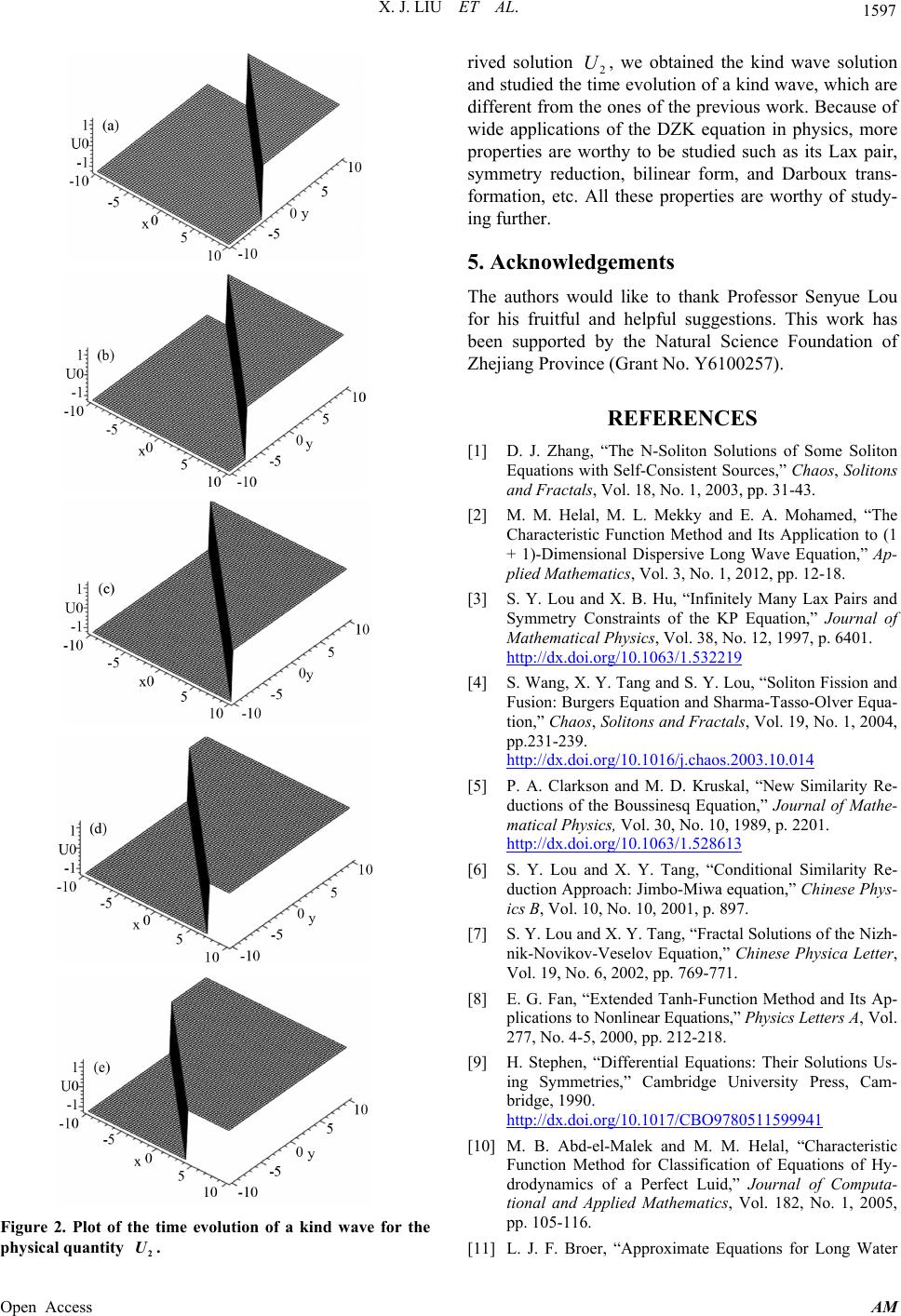 X. J. LIU ET AL. 1597 Figure 2. Plot of the time evolution of a kind wave for the physical quantity rived solution , we obtained the kind wave solution and studied the evolution of a kind wave, which are different from the ones of the previous work. Because of wide applications of the DZK equation in physics, more properties are worthy to be studied such as its Lax pair, symmetry reduction, bilinear form, and Darboux trans- formation, etc. All these properties are worthy of study- ing further. 5. Acknowledgements The authors would like to thank Professor Senyue Lou for his fruitful and helpful suggestions. This work has been supported by the Natural Science Foundation of Zhejiang Province (Grant No. Y6100257). REFERENCES [1] D. J. Zhang, “The N-Soliton Solutions of Some Soliton Equations with Self-Consistent Sources,” Chaos, Solitons and Fractals, Vol. 18, No. 1, 2003, pp. 31-43. [2] M. M. Helal, M. L. Mekky and E. A. Mohamed, “The n a 2 U. 2 U e tim Characteristic Function Method and Its Application to (1 + 1)-Dimensioal Dispersive Long Wave Equation,” Ap- plied Mathems, Vol. 3tic , No. 1, 2012, pp. 12-18. [3] S. Y. Lou and X. B. Hu, “Infinitely Many Lax Pairs and Symmetry Constraints of the KP Equation,” Journal of Mathematical Physics, Vol. 38, No. 12, 1997, p. 6401. http://dx.doi.org/10.1063/1.532219 [4] S. Wang, X. Y. Tang and S. Y. Lou, “Soliton Fission and Fusion: Burgers Equation and Sharma-Tasso-Olver Equa- tion,” Chaos, Solitons and Fractals, Vol. 19, No. 1, 2004, pp.231-2 http://dx.doi.org/10.1016/j.ch 39. aos.2003.10.014 Kruskal, “New Similarity Re- Equation,” Journal of Mathe- [5] P. A. Clarkson and M. D. ductions of the Boussinesq matical Physics, Vol. 30, No. 10, 1989, p. 2201. http://dx.doi.org/10.1063/1.528613 [6] S. Y. Lou and X. Y. Tang, “Conditional Similarity Re- duction Approach: Jimbo-Miwa equation,” Chinese Phys- ics B, Vol. 10, No. 10, 2001, p. 897. [7] S. Y. Lou andions of the Nizh- nik-Novikov-V ese Physica Letter, rs A, Vol. X. Y. Tang, “Fractal Solut eselov Equation,” Chin Vol. 19, No. 6, 2002, pp. 769-771. [8] E. G. Fan, “Extended Tanh-Function Method and Its Ap- plications to Nonlinear Equations,” Physics Lette 277, No. 4-5, 2000, pp. 212-218. [9] H. Stephen, “Differential Equations: Their Solutions Us- ing Symmetries,” Cambridge University Press, Cam- bridge, 1990. http://dx.doi.org/10.1017/CBO9780511599941 [10] M. B. Abd-el-Malek and M. M. Helal, “Characteristic Function Method for Classification of Equations of H drodynamics of a Perfect Luid,” Jou y- rnal of Computa- tional and Applied Mathematics, Vol. 182, No. 1, 2005, pp. 105-116. [11] L. J. F. Broer, “Approximate Equations for Long Water Open Access AM  X. J. LIU ET AL. Open Access AM 1598 lied Scientific Research, Vol. 31, No. 5, Waves,” App 1975, pp. 377-395. http://dx.doi.org/10.1007/BF00418048 [12] D. J. Kaup, “Finding Eigenvalue Problems for Solving Nonlinear Evolution Equations,” Progress of The Physics, Vol. 54, No. 1, 1975, pp. 72 o -78. l of Mathematica retical [13] L. Martinez, “Schrodinger Spectral Problems with En- ergy-Dependent Potentials as Sources of Nonlinear Ham- iltonian Evolution Equations,” Journal Physics, Vol. 21, No. 9, 1980, pp. 2342-2349. http://dx.doi.org/10.1063/1.524690 [14] B. A. Kupershmidt, “Mathematics of Dispersive Water Waves,” Communications in Mathematical Physics, Vol. 99, No. 1, 1985, pp. 51-73. http://dx.doi.org/10.1007/BF01466593 [15] X. Y. Tang and S. Y. Lou, “Localized Excitations in (2 + 1)-Dimensional Systems,” Physical Review E, Vol. 66, No. 4, 2002, Article ID: 046601. [16] S. H. Ma, X. H. Wu, J. P. Fang and C. L. Zheng, “Chaotic nteraction viours of (2 + 1)-Di- romion Soliton Background of ng, “Folded Locailzed t Solution and 11-0063 Solitons for the (2 + 1)-Dimensional Modified Dispersive Water-Wave System,” Zeitschrift für Naturforschung A, Vol. 61, No. 1, 2007, pp. 249-252. [17] S. H. Ma, J. Y. Qiang and J. P. Fang, “The I between Solitons and Chaotic Beha mensional Boiti-Leon-Pempinelli System,” Acta Physics Sinica, Vol. 56, No. 2, 2007, pp. 620-626. [18] S. H. Ma, J. P. Fang and H. P. Zhu, “D Waves and the Their Evolution in the Jacobi Sine Waves,” Acta Physics Sinica, Vol. 56, No. 8, 2007, pp. 4319-4325. [19] S. H. Ma, J. P. Fang and C. L. Zhe Excitations and Chaotic Patterns in a (2 + 1)-Dimensional Soliton System,” Zeitschrift für Naturforschung A, Vol. 62, No. 1, 2008, pp. 121-126. [20] B. Q. Li, S. Li and Y. L. Ma, “New Exac Novel Time Solitons for the Dissipative Zabolotskaya Khokhlov Equation from Nonlinear Acoustics,” Zeit- schrift für Naturforschung A, Vol. 67, No. 11, 2012, pp. 601-607. http://dx.doi.org/10.5560/ZNA.20
|