Wireless Sensor Network, 2009, 1, 1-60
Published Online April 2009 in SciRes (http://www.SciRP.org/journal/wsn/).
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
Bandwidth Efficient Three-User Cooperative Diversity
Scheme Based on Relaying Superposition Symbols
Mingwei CAO, Guangguo BI, Xiufeng JIN
National Mobile Communications Research Laboratory, Southeast University, Nanjing, China
Received February 3, 2009; revised February 17, 2009; accepted February 19, 2009
Abstract
Recently, Cooperative diversity in wireless communication systems has gained much attention. A simple
two-user cooperative diversity scheme called decode-and-forward cooperation scheme has been presented by
Laneman (2004). Each user has one partner to decode its information and retransmit it by employing repeti-
tion coding. This scheme can offer diversity order of two. But the bandwidth efficiency is low. In this paper,
we propose a bandwidth efficient three-user cooperative diversity scheme based on relaying superposition
symbols. Each user has two partners and each partner relays superposition symbols of the other two users
instead of repetition. Thus, the bandwidth efficiency is improved compared to the baseline decode-
and-forward cooperative diversity scheme presented by Laneman. Moreover, the proposed scheme can also
offer diversity order of two. Then, in order to improve the system performance, a new constellation labeling
for the superposition 8PSK modulation is designed. It is a simple way to exploit the symbol mapping diver-
sity and a gain of about 2 dB can be obtained. Furthermore, the performance improvement comes at no addi-
tional power or bandwidth expense.
Keywords: Cooperative Diversity, Bandwidth Efficiency, Superposition Symbols, Symbol Mapping Diversity
1. Introduction
Multiple-antenna technique has been studied extensively,
and it is an efficient technique to exploit spatial diversity
and offer capacity gain compared to single-antenna sys-
tems [1,2]. Transmit diversity [3] has been proposed to
improve the performance for systems with multiple
transmit antennas.
However, in wireless communication systems, users
may not be able to support multiple antennas because of
the limitation of the size or cost. In this scenario, coop-
erative diversity, which has been proposed to achieve the
transmit diversity, has gained much attention when each
user only has a single antenna [4,5]. In cooperative
communication systems [6,7], each user transmits its
information to a destination and receives its partners’
information and then serves as a relay for its partners.
Hence, the destination can receive each user’s informa-
tion from several independent paths to efficiently resist
the slowly fading effect. In baseline decode-and-forward
cooperation scheme [7], two users transmit their infor-
mation on orthogonal channels. Each user has one part-
ner and decodes the partner’s information and re-encodes
and retransmits it through its own channel, thus, the di-
versity order is two. However, the bandwidth efficiency
is decreased by 1/2 compared to a non-cooperative di-
versity scheme. In order to reduce the bandwidth loss,
some cooperation schemes are proposed in [8-12]. In [8],
distributed space-time codes are used for cooperating
transmission. Multi-source cooperation coding approach
is introduced in [9-12]. In those cooperation schemes,
data of multiple users are jointly encoded by relays. The
bandwidth efficiency of these schemes presented in [8-12]
is improved greatly, but the decoding complexity is too high.
In this paper, we propose a cooperative diversity
scheme based on superposition modulation, which offers
the same diversity order as the baseline decode-and-
forward cooperation scheme does. The bandwidth effi-
ciency of the proposed scheme is only decreased by 1/3
compared to a non-cooperative diversity scheme and the
decoding complexity is much lower than that of these
schemes presented in [8-12]. Moreover, a new constella-
tion labeling for the superposition modulation is de-
signed to improve the bit error rate (BER) performance
when the system employs 8PSK modulation. Using the

2 M. W. CAO ET AL.
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
new constellation labeling, the system performance can
be improved without any additional power or bandwidth
expense.
Also, a cooperation scheme of two-node system
based on superposition BPSK modulation is proposed in
[13]. In this system, each node transmits a superposition
of its own data with the data received from its partner in
the previous slot. The performance of this scheme pre-
sented in [13] is further analyzed in [14,15]. In [16], the
generalization of the scheme proposed in [13] to a multi-
ple-user scenario is considered. In [17], a novel coopera-
tion scheme based on the algebraic superposition of
channel codes over a finite field is proposed. In [18],
user and relay use the in-phase and the quadrature com-
ponents of a QPSK signal, respectively for cooperating
transmission. These schemes proposed in [13-18] are
different from our scheme in which each partner re-
transmits the superposition symbols received from dif-
ferent users and each user’s own symbols are not super-
posed with its partners’ symbols.
The rest of this paper is organized as follows. In Sec-
tion 2, system model is introduced, and a bandwidth effi-
cient cooperative diversity scheme is proposed. The di-
versity order is discussed in Section 3 and a new symbol
mapping is designed in Section 4. The simulation results
are described in Section 5. Finally, conclusions are
summarized in Section 6.
2. System Model
In this scheme, three users (A, B, and C) transmit their
information to a destination (D). Assume that all chan-
nels between users and the destination (uplink channels)
are Rayleigh flat slowly fading channels, which remain
constant over at least six slots. We consider multiple
access channels as time-division multiple access (TD
MA). Thus, these users transmit in their own slots, re-
spectively. If symbols ai, bi and ci, which take values
from an M-ary alphabet
{}
01 1
,, ,
M
ss s
−
K, are transmitted
from these users through three orthogonal channels, re-
spectively, then the received baseband signals r1i, r2i and
r3i in the destination can be written as
11iADi
rhan=+ (1)
22iBDi
rhbn=+ (2)
33iCDi
rhcn=+ (3)
where hAD, hBD, and hCD are channel fading coefficients
between users A, B, C, and the destination D, respec-
tively, and n1, n2, and n3 are additive noises. They are all
modeled as independent complex zero-mean Gaussian
random variables, and
{}{}{}
222
1
ADBD CD
hhh εεε ===
 (4)
and
{}{}{}
222
1230
nnnN εεε ===
(5)
(a) System model of the baseline two-user cooperation scheme.
(
)
11
bc β +
()
12
ac β +
L
L
L
L
(
)
22
ab β +
(b) System model of the proposed cooperation scheme.
Figure 1. System models of the baseline and the proposed
cooperation schemes.
Note that
ε
denotes the expectation operator.
Simultaneously, each user receives the other users’
information through the channels between users (in-
ter-user channels) and relays its partners’ information
only if it decodes correctly, which can be determined by
the cyclic redundancy check (CRC). The destination is
assumed to be informed of whether relays decode cor-
rectly or not. Generally speaking, the user is close to its
partners and they may have line-of-sight connections.
Thus, the quality of inter-user channels is better than that
of uplink channels. In this paper, we take inter-user
channels to be additive white Gaussian noise (AWGN)
when line-of-sight connections exist.
2.1. Baseline Scheme
The decode-and-forward cooperation scheme presented
in [7] is regarded as a baseline scheme. The system
model of two-user cooperation scheme is shown in Fig-
ure 1 (a). Each slot is divided into two segments with the
same length of time. Each user transmits its own symbols
in the first segment and remains inactive in the second
segment. The partner receives these symbols in the first
segment, and then retransmits these symbols by employ-
ing repetition coding in the second segment if it decodes
correctly, otherwise, it remains inactive.
2.2. Proposed Scheme
The system model of the proposed cooperation scheme is
shown in Figure 1(b). Each slot is divided into three seg-
ments with the same length of time. In the first slot, user
A transmits its own symbols a1 and a2 in the first two
segments, respectively, and remains inactive in the third
segment. User B only detects a1 in the first segment and
user C only detects a2 in the second segment. Coopera-
L
L
L
SLOT
k
SLOT k+1
A
B

M. W. CAO ET AL. 3
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
tion processes are similar in the second and third slots
(see Figure 1(b)).
In the fourth slot, user A transmits its own symbols a3
and a4 in the first two segments, respectively, and the
superposition symbol
()
11
bc β + in the third segment if
both of b1 and c1 are decoded correctly, where
β
is a
power-normalizing scalar. In this paper, we set
22 β = to satisfy the transmit-power constraint. If
user A can only decode the symbol of user B (or user C)
correctly, then user A only retransmits b1 (or c1) instead
of
()
11
bc β + in the third segment. If neither of the
symbols of user B and user C can be decoded correctly,
then user A remains inactive in the third segment. User B
detects a3 in the first segment and user C detects a4 in the
second segment. Also, cooperation processes are similar
in the fifth and sixth slots (see Figure 1(b)).
In the following slots, similar cooperation processes to
those executed in the fourth to sixth slots are executed. In
the last three slots, each user remains inactive in the first
two segments and only retransmits the superposition
symbol in the third segment.
Each user transmits its own symbols in two segments
and serves as a relay for other users in only one segment.
We assume that the total number of slots is large so that
the loss of overhead in the first three slots can be ne-
glected. Therefore, the bandwidth efficiency is only de-
creased by 1/3 compared to a non-cooperative diversity
scheme.
In this scheme, symbols received from two different
partners are superposed, and then the superposition
symbols are retransmitted from the user. This can pro-
vide diversity order of two. However, if symbols re-
ceived from each partner are superposed, respectively,
and then retransmitted from the user, the diversity order
of two will not be achieved.
3. Diversity Order
Assume that perfect channel state information is avail-
able in the receiver and ideal cooperation is considered,
which means each user can always decode other users’
information correctly. The maximum-likelihood (ML)
decoder in the destination works with pairs of transmit-
ted symbols instead of single symbols. Thus, the decod-
ing complexity is higher, but it is still much lower than
that of the schemes presented in [8-12].
Assume that M-PSK (4
M
≥) modulation is employed
and Gray code is used to map bits to symbols. Without
loss of generality, we consider the pair of symbols ai and
bi, where
{}
01 1
,,,,
ii M
abs ss− ∈K. Assume that ai, bi and
()
2
2+
ii
ab are transmitted from user A, B and C, re-
spectively, the corresponding received baseband signals
are r1i, r
2i and r3i. The receiver computes the decision
metric
()
2
22
123
2
2
+
−+−+−
CD ii
iADiiBDi i
hab
rha rhb r (6)
over all possible pairs of symbols
{}
,
ii
ab , and a deci-
sion is made in favor of the pair of symbols that mini-
mizes the metric.
There will be three cases for each decision.
case 0: The decision is correct.
case 1: The decision results in one symbol error.
case 2: The decision results in two symbol errors.
The probability of case 1 for each decision is
(
)
()
()
Pr 1
Prisdecoded correctly,is decoded incorrectly
Pris decoded incorrectly,is decodedcorrectly
ii
ii
case
ab
ab
=
+

(7)
Equation (7) can be approximated as
()
()
()
22
2
min
0
22
2
min
0
2
Pr1 22
2
2
AD CD
BD CD
hh d
case QN
hh d
QN
ε
⎧⎛⎞
+
⎪⎜⎟
≈⎨⎜⎟
⎪⎜⎟
⎝⎠
⎩
⎫
⎛⎞
+
⎪
⎜⎟
+⎬
⎜⎟
⎪
⎜⎟
⎝⎠
⎭
(8)
where
(
)
Q
⋅
is the Gaussian Q-function and dmin is the
minimum Euclidean distance between pairs of signal
points in the constellation. Let
(
)
2
min 0
8dN γ = (9)
then (8) can be simplified as [19]
()
2
Pr1224
112
case
γ
γ
γ
γ
≈+ −
++
 (10)
when 1
γ
>> , the probability is
()
2
3
Pr1 8 case
γ
−
≈ (11)
If the receiver decides erroneously in favor of symbols
i
a
′
(ii aa
′
≠
) and i b
′
(ii bb
′
≠
), the value ii ab
′
′
+
may
be probably equal to the value ii
ab+. Thus, the probabil-
ity of case 2 for each decision can be upper-bounded as
()
()
22
2
min
0
2
Pr2 22
12 2
21
212 12
AD BD
hhd
case QN ε
γγ
γγ
⎧
⎫
⎛⎞
+
⎪
⎪
⎜⎟
<
⎨
⎬
⎜⎟
⎪
⎪
⎜⎟
⎝⎠
⎩⎭
⎛⎞⎛⎞
=+ −
⎜⎟⎜⎟
⎜⎟⎜⎟
++
⎝⎠⎝⎠
(12)

4 M. W. CAO ET AL.
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
when 12
γ
>> , we obtain
()
2
3
Pr2 32 case
γ
−
< (13)
From (11) and (13), we can conclude that each erro-
neous decision most results in one symbol error and the
average BER for each user is approximated as
()
2
2
2
11
Pr 1
log 2
13
log 16
b
pcase
M
M
γ
−
≈×
≈×
(14)
which shows that the diversity order of two is achieved.
In baseline decode-and-forward cooperation scheme,
the average BER for each user is approximated as
2
2
13
log 32
b
pM
γ
−
′≈×
 (15)
4. Design of Symbol Mapping
We observed from (14) and (15) that there is signal-
to-noise ratio (SNR) loss for the proposed scheme com-
pared to the baseline scheme. That is mainly because the
power of the superposition symbol is equal to that of a
single symbol transmitted in the first two segments in the
proposed scheme. The total average energy for each
symbol in the proposed scheme is 3/4 times as large as
that in the baseline scheme. However, we can mitigate
the SNR loss by exploiting symbol mapping diversity.
In most communication systems, multi-level modula-
tion techniques such as M-PAM, M-PSK and M-QAM
are employed to improve the bandwidth efficiency and
the bit-to-symbol mapping for those modulation constel-
lations is Gray code bit mapping. However, some en-
hanced Automatic Repeater request (ARQ) schemes
[20-23] to extract additional diversity called symbol
mapping diversity between retransmissions have been
proposed. In those schemes, for exploiting the symbol
mapping diversity, the bit-to-symbol mapping for the
second transmission (first retransmission) is not Gray
code bit mapping. For example, in the scheme proposed
in [21], Gray code bit mapping is employed in the first
transmission and another different symbol mapping is
employed for maximizing the minimum combined
squared Euclidean distance (CESD) [21] in the second
-1 0 1
-1
0
1
0
1
4
3
5
6
7
2
Figure 2. Signal constellation of 8PSK modulation.
transmission. The method proposed in [21] is further
discussed in [22] and a symbol mapping diversity
scheme in Multiple-Input Multiple-Output (MIMO) sys-
tems is presented in [23]. The symbol mapping diversity
can provide great BER gains in AWGN and Rayleigh flat
fading channels. In this paper, we design a new symbol
mapping for superposition 8PSK modulation.
The superposition symbols lead to a superposition
modulation and we use Gray code bit mapping for 8PSK
modulation and another symbol mapping for superposi-
tion modulation. The constellation of 8PSK modulation
is showed in Figure 2. Each point represents an 8PSK
symbol, which is labeled by 3 bits represented as an octal
number. Since each erroneous decision most results in one
symbol error and erroneous selection of an adjacent sym-
bol, these distances between pairs of signal points, such as
(
)
{
}
() {}
,0, ,7
ij ik
ji ki
ss ss
ijkandjk
ss ss
⎧↔
⎪
≤
≤≠
⎨↔
⎪
⎩
 (16)
which differ in only a symbol and two different symbols
sj and sk are adjacent in 8PSK constellation, should be
increased as large as possible in the superposition con-
stellation. Based on this principle, the constellation of the
superposition 8PSK modulation is designed and shown
in Figure 3. Each point represents the superposition of
two 8PSK symbols, which is labeled by 6 bits repre-
sented as two octal numbers.
5. Simulation Results
In the simulation, we assume that uplink channels are
Rayleigh flat slowly fading channels. When we suppose
that there exist line-of-sight connections, inter-user
channels are assumed to be AWGN channels. Otherwise,
inter-user channels are assumed to be Rayleigh flat
slowly fading channels. In baseline decode-and-forward
cooperation scheme, each user employs repetition coding
to relay its partner’s information. Set the symbol energy
as Es and assume that all inter-user channels have equal
average SNR and so do all uplink channels.
-1.5-1 -0.500.5 11. 5
-1. 5
-1
-0. 5
0
0.5
1
1.5 75
46 64
71 17 60 06
53 35 42 24
22 45
07 70
54
15
51
40
34
43
01 02 20
13
16 6132
37
73
26
25
52
67
33 57
11
76
00
62
44 23
55 31
10
77
04
66
12 21
03
30
14
41
05
50
47 74
56
65
27
72
36
63
Figure 3. Signal constellation of superposition 8PSK
modulation.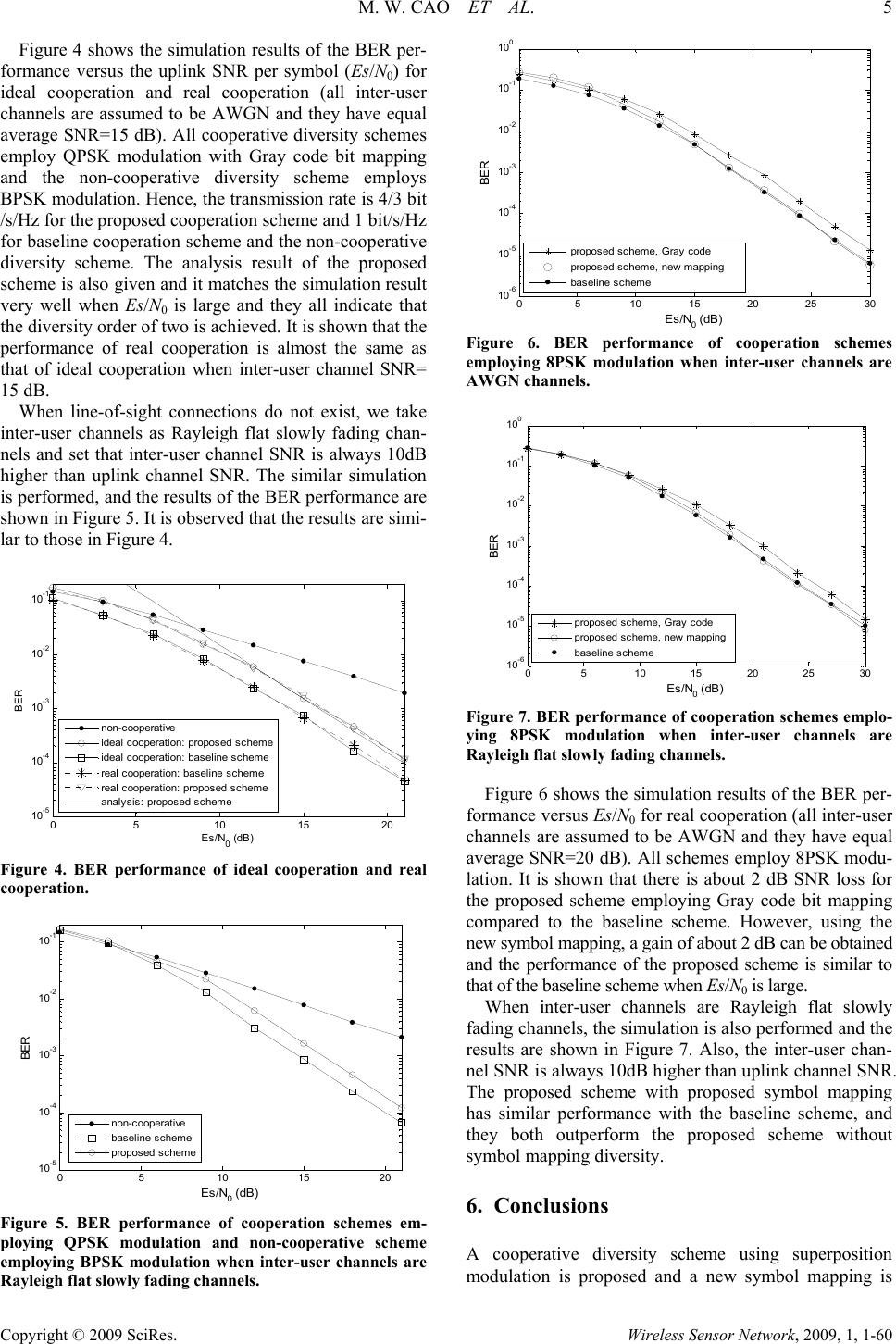

M. W. CAO ET AL. 5
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
Figure 4 shows the simulation results of the BER per-
formance versus the uplink SNR per symbol (Es/N0) for
ideal cooperation and real cooperation (all inter-user
channels are assumed to be AWGN and they have equal
average SNR=15 dB). All cooperative diversity schemes
employ QPSK modulation with Gray code bit mapping
and the non-cooperative diversity scheme employs
BPSK modulation. Hence, the transmission rate is 4/3 bit
/s/Hz for the proposed cooperation scheme and 1 bit/s/Hz
for baseline cooperation scheme and the non-cooperative
diversity scheme. The analysis result of the proposed
scheme is also given and it matches the simulation result
very well when Es/N0 is large and they all indicate that
the diversity order of two is achieved. It is shown that the
performance of real cooperation is almost the same as
that of ideal cooperation when inter-user channel SNR=
15 dB.
When line-of-sight connections do not exist, we take
inter-user channels as Rayleigh flat slowly fading chan-
nels and set that inter-user channel SNR is always 10dB
higher than uplink channel SNR. The similar simulation
is performed, and the results of the BER performance are
shown in Figure 5. It is observed that the results are simi-
lar to those in Figure 4.
05 10 15 20
10
-5
10
-4
10
-3
10
-2
10
-1
Es/N
0
(dB)
BE
R
non-cooperative
ideal cooperation: proposed scheme
ideal cooperation: baseline scheme
real cooperation: baseline scheme
real cooperation: proposed scheme
analysis: proposed scheme
Figure 4. BER performance of ideal cooperation and real
cooperation.
05 10 15 20
10
-5
10
-4
10
-3
10
-2
10
-1
Es /N
0
(dB)
BER
non-cooperative
baseline scheme
proposed scheme
Figure 5. BER performance of cooperation schemes em-
ploying QPSK modulation and non-cooperative scheme
employing BPSK modulation when inter-user channels are
Rayleigh flat slowly fading channels.
05 1015 20 2530
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Es/N
0
(dB)
BER
proposed scheme, Gray code
proposed scheme, new mapping
baseline scheme
Figure 6. BER performance of cooperation schemes
employing 8PSK modulation when inter-user channels are
AWGN channels.
05 10 1520 2530
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
Es/N
0
(dB)
BER
proposed scheme, Gray code
proposed scheme, new mapping
baseline scheme
Figure 7. BER performance of cooperation schemes emplo-
ying 8PSK modulation when inter-user channels are
Rayleigh flat slowly fading channels.
Figure 6 shows the simulation results of the BER per-
formance versus Es/N0 for real cooperation (all inter-user
channels are assumed to be AWGN and they have equal
average SNR=20 dB). All schemes employ 8PSK modu-
lation. It is shown that there is about 2 dB SNR loss for
the proposed scheme employing Gray code bit mapping
compared to the baseline scheme. However, using the
new symbol mapping, a gain of about 2 dB can be obtained
and the performance of the proposed scheme is similar to
that of the baseline scheme when Es/N0 is large.
When inter-user channels are Rayleigh flat slowly
fading channels, the simulation is also performed and the
results are shown in Figure 7. Also, the inter-user chan-
nel SNR is always 10dB higher than uplink channel SNR.
The proposed scheme with proposed symbol mapping
has similar performance with the baseline scheme, and
they both outperform the proposed scheme without
symbol mapping diversity.
6. Conclusions
A cooperative diversity scheme using superposition
modulation is proposed and a new symbol mapping is

6 M. W. CAO ET AL.
Copyright © 2009 SciRes. Wireless Sensor Network, 2009, 1, 1-60
designed. The bandwidth efficiency of the proposed
scheme is more efficient than that of the baseline decode-
and-forward cooperation scheme because of superposi-
tion modulation. Moreover, it is demonstrated that the
BER performance of the proposed scheme with the pro-
posed symbol mapping is almost the same as that of the
baseline cooperation scheme employing 8PSK modula-
tion and the decoding complexity is moderate.
7. Acknowledgement
This work was supported by the Research Fund of Na-
tional Mobile Communications Research Laboratory,
Southeast University under Grant No. 2008A05, by the
National Basic Research Program of China under Grant
2007CB310603, by China 863 Project under Grant No.
2007AA01Z2B1, and by NSFC Project under Grant No.
60802005.
9. References
[1] G. J. Foschini and M. J. Gans, “On limits of wireless
communications in a fading environment when using
multiple antennas,” Wireless Personal Communications,
Vol. 6, No. 3, pp. 311-335, 1998.
[2] E. Telatar, “Capacity of multi-antenna Gaussian channels,”
European Transactions on Telecommuni- cations, Vol. 10,
No. 6, pp. 585-596, 1999.
[3] S. M. Alamouti, “A simple transmit diversity technique
for wireless communications,” IEEE Journal on Selected
Areas in Communications, Vol. 16, No. 8, pp. 1451-1458,
1998.
[4] A. Sendonaris, E. Erkip, and B. Aazhang, “User cooperation
diversity Part I: System description,” IEEE Transactions
on Communications, Vol. 51, No. 11, pp. 1927-1938,
November 2003.
[5] A. Sendonaris, E. Erkip, and B. Aazhang, “User cooperation
diversity Part II: Implementation aspects and performance
analysis,” IEEE Transactions on Communications, Vol.
51, No. 11, pp. 1939-1948, November 2003.
[6] A. Nosratinia, T. E. Hunter, and A. Hedayat, “Co-
operative communication in wireless networks,” IEEE
Communications Magazine, Vol. 42, No. 10, pp. 74-80,
October 2004.
[7] J. N. Laneman, D. N. C. Tse, and G. W. Wornell,
“Cooperative diversity in wireless networks: Efficient
protocols and outage behavior,” IEEE Transactions on
Information Theory, Vol. 50, No. 12, pp. 3062-3080,
December 2004.
[8] J. N. Laneman and G. W. Wornell, “Distributed space-
time-coded protocols for exploiting cooperative diversity
in wireless networks,” IEEE Transactions on Information
Theory, Vol. 49, No. 10, pp. 2415-2425, October 2003.
[9] O. Shalvi, “Multiple source cooperation diversity,” IEEE
Communications Letters, Vol. 8, No. 12, pp. 712-714,
December 2004.
[10] R. Q. Wang, W. L. Zhao, and G. B. Giannakis,
“Multi-source cooperative networks with distributed
convolutional coding,” 2005 Conference Record of the
Thirty-Ninth Asilomar Conference on Signals, Systems
and Computers, pp. 1056-1060, 2005.
[11] R. Q. Wang, W. L. Zhao, and G. B. Giannakis,
“Distributed trellis coded modulation for multi-source
cooperative networks,” Radio and Wireless Symposium,
2006 IEEE, San Diego, CA, pp. 271-274, January 2006.
[12] R. Q. Wang and G. B. Giannakis, “Complex field coding
in multi-source cooperative networks for full diversity,”
2006 IEEE International Conference on Communications,
Vol. 10, pp. 4485-4488, June 2006.
[13] E. G. Larsson and B. R. Vojcic, “Cooperative transmit
diversity based on superposition modulation,” IEEE
Communications Letters, Vol. 9, No. 9, pp. 778-780,
September 2005.
[14] Z. G. Ding, T. Ratnarajah, and C. Cowan, “On the
performance of superposition cooperative diversity in
wireless networks,” 2006 IEEE International Symposium
on Information Theory, pp. 2714-2718, July 2006.
[15] K. Ishii, “Cooperative transmit diversity utilizing
superposition modulation,” Radio and Wireless
Symposium, 2007 IEEE, pp. 337-340, January 2007.
[16] Z. G. Ding, T. Ratnarajah, and C. C. F. Cowan, “On the
divesity-multiplexing tradeoff for wireless cooperative
multiple access systems,” IEEE Transactions on Signal
Processing, Vol. 55, No. 9, pp. 4627-4638, September 2007.
[17] L. Xiao, T. E. Fuja, J. Kliewer, and D. J. Costello,
“Cooperative diversity based on code superposition,”
2006 IEEE International Symposium on Information
Theory, pp. 2456-2460, July 2006.
[18] V. Mahinthan, J. W. Mark, and X. M. Shen, “A coopera-
tive diversity scheme based on quadrature signaling,”
IEEE Transaction on Wireless Communications, Vol. 6,
No. 1, pp. 41-45, January 2007.
[19] M. K. Simon and M. Alouini, “A unified approach to the
performance analysis of digital communication over
generalized fading channels,” Proceedings of IEEE, Vol.
86, No. 9. pp. 1860-1877, September 1998.
[20] C. Wengerter, A. G. Edler von Elbwart, E. Seidel, G.
Velev, and M. P. Schmitt, “Advanced hybrid ARQ
technique empolying a signal constellation rearrage-
ment,” in Proceedings of IEEE VTC 2002 Fall, Vol. 4, pp.
2002-2006, September 2002.
[21] H. Samra, Z. Ding, and P. M. Hahn, ”Symbol mapping
diversity design for multiple packet transmissions,” IEEE
Transactions on Communications, Vol. 53, No. 5, May 2005.
[22] M. Gidlund, “Performance of hybrid ARQ scheme based
on bit-to-symbol mapping,” 2008 IET International
Conference on Wireless, Mobile and Multimedia
Networks, pp. 303-306, January 2008.
[23] S. H. Moon, H. H. Park, A. Goldsmith, and M. S. Oh,
“Bit rearrangement for MIMO retransmissions,” Global
Telecommunications Conference, 2007, GLOBECOM ’07
IEEE, pp. 3509–3513, November 2007.