W. W. CAO ET AL. 185
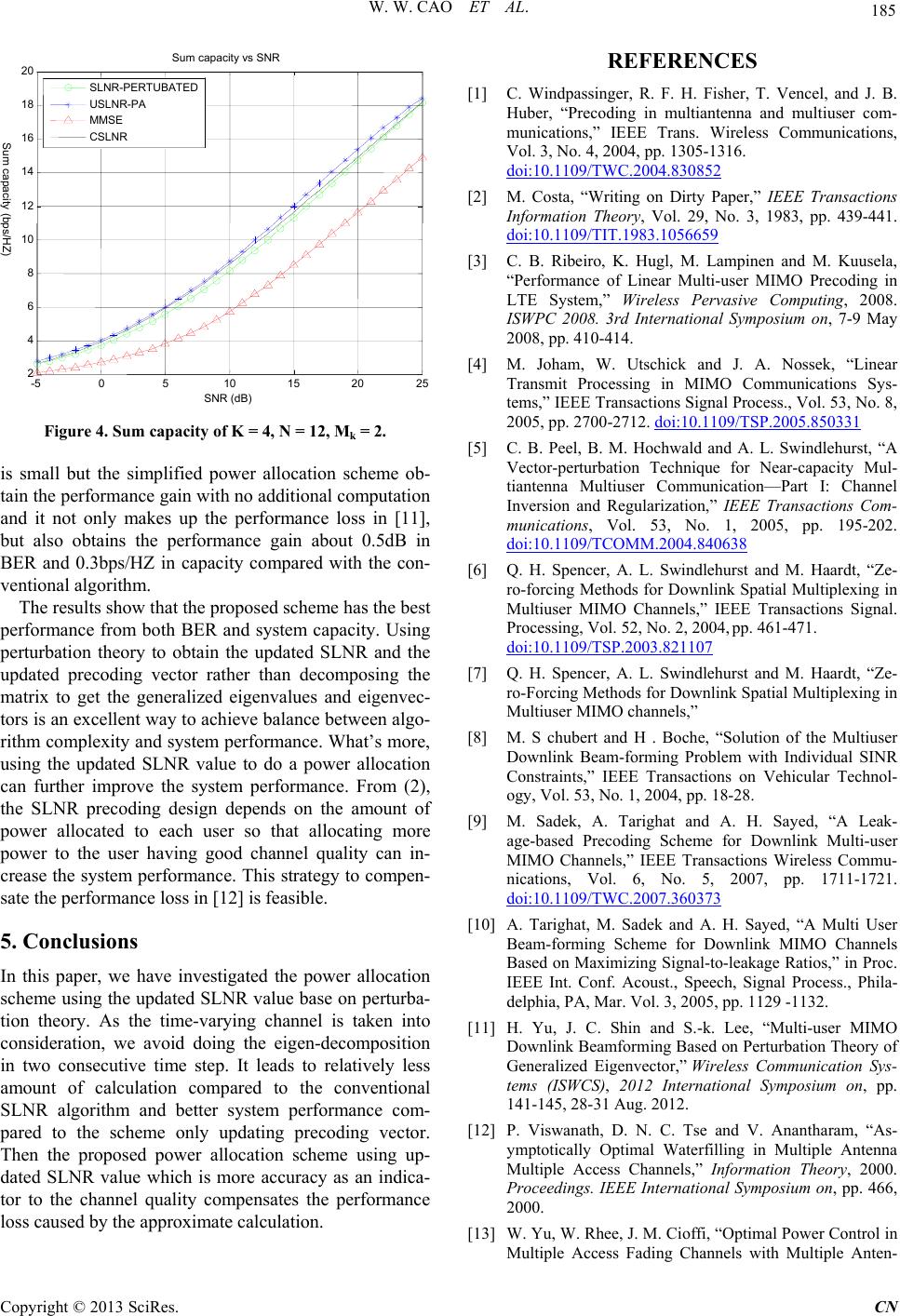
Figure 4. Sum capacity of K = 4, N = 12, Mk = 2.
is small but the simplified power allocation scheme ob-
tain the performance gain with no additional computation
and it not only makes up the performance loss in [11],
but also obtains the performance gain about 0.5dB in
BER and 0.3bps/HZ in capacity compared with the con-
ventional algorithm.
The results show that the proposed scheme has the best
performance from both BER and system capacity. Using
perturbation theory to obtain the updated SLNR and the
updated precoding vector rather than decomposing the
matrix to get the generalized eigenvalues and eigenvec-
tors is an excellent way to achieve balance between algo-
rithm complexity and system performance. What’s more,
using the updated SLNR value to do a power allocation
can further improve the system performance. From (2),
the SLNR precoding design depends on the amount of
power allocated to each user so that allocating more
power to the user having good channel quality can in-
crease the system performance. This strategy to compen-
sate the performance loss in [12] is feasible.
5. Conclusions
In this paper, we have investigated the power allocation
scheme using the updated SLNR value base on perturba-
tion theory. As the time-varying channel is taken into
consideration, we avoid doing the eigen-decomposition
in two consecutive time step. It leads to relatively less
amount of calculation compared to the conventional
SLNR algorithm and better system performance com-
pared to the scheme only updating precoding vector.
Then the proposed power allocation scheme using up-
dated SLNR value which is more accuracy as an indica-
tor to the channel quality compensates the performance
loss caused by the approximate calculation.
REFERENCES
[1] C. Windpassinger, R. F. H. Fisher, T. Vencel, and J. B.
Huber, “Precoding in multiantenna and multiuser com-
munications,” IEEE Trans. Wireless Communications,
Vol. 3, No. 4, 2004, pp. 1305-1316.
doi:10.1109/TWC.2004.830852
[2] M. Costa, “Writing on Dirty Paper,” IEEE Transactions
Information Theory, Vol. 29, No. 3, 1983, pp. 439-441.
doi:10.1109/TIT.1983.1056659
[3] C. B. Ribeiro, K. Hugl, M. Lampinen and M. Kuusela,
“Performance of Linear Multi-user MIMO Precoding in
LTE System,” Wireless Pervasive Computing, 2008.
ISWPC 2008. 3rd International Symposium on, 7-9 May
2008, pp. 410-414.
[4] M. Joham, W. Utschick and J. A. Nossek, “Linear
Transmit Processing in MIMO Communications Sys-
tems,” IEEE Transactions Signal Process., Vol. 53, No. 8,
2005, pp. 2700-2712. doi:10.1109/TSP.2005.850331
[5] C. B. Peel, B. M. Hochwald and A. L. Swindlehurst, “A
Vector-perturbation Technique for Near-capacity Mul-
tiantenna Multiuser Communication—Part I: Channel
Inversion and Regularization,” IEEE Transactions Com-
munications, Vol. 53, No. 1, 2005, pp. 195-202.
doi:10.1109/TCOMM.2004.840638
[6] Q. H. Spencer, A. L. Swindlehurst and M. Haardt, “Ze-
ro-forcing Methods for Downlink Spatial Multiplexing in
Multiuser MIMO Channels,” IEEE Transactions Signal.
Processing, Vol. 52, No. 2, 2004, pp. 461-471.
doi:10.1109/TSP.2003.821107
[7] Q. H. Spencer, A. L. Swindlehurst and M. Haardt, “Ze-
ro-Forcing Methods for Downlink Spatial Multiplexing in
Multiuser MIMO channels,”
[8] M. S chubert and H . Boche, “Solution of the Multiuser
Downlink Beam-forming Problem with Individual SINR
Constraints,” IEEE Transactions on Vehicular Technol-
ogy, Vol. 53, No. 1, 2004, pp. 18-28.
[9] M. Sadek, A. Tarighat and A. H. Sayed, “A Leak-
age-based Precoding Scheme for Downlink Multi-user
MIMO Channels,” IEEE Transactions Wireless Commu-
nications, Vol. 6, No. 5, 2007, pp. 1711-1721.
doi:10.1109/TWC.2007.360373
[10] A. Tarighat, M. Sadek and A. H. Sayed, “A Multi User
Beam-forming Scheme for Downlink MIMO Channels
Based on Maximizing Signal-to-leakage Ratios,” in Proc.
IEEE Int. Conf. Acoust., Speech, Signal Process., Phila-
delphia, PA, Mar. Vol. 3, 2005, pp. 1129 -1132.
[11] H. Yu, J. C. Shin and S.-k. Lee, “Multi-user MIMO
Downlink Beamforming Based on Perturbation Theory of
Generalized Eigenvector,” Wireless Communication Sys-
tems (ISWCS), 2012 International Symposium on, pp.
141-145, 28-31 Aug. 2012.
[12] P. Viswanath, D. N. C. Tse and V. Anantharam, “As-
ymptotically Optimal Waterfilling in Multiple Antenna
Multiple Access Channels,” Information Theory, 2000.
Proceedings. IEEE International Symposium on, pp. 466,
2000.
[13] W. Yu, W. Rhee, J. M. Cioffi, “Optimal Power Control in
Multiple Access Fading Channels with Multiple Anten-
-5 0 5 10 15 20
20
25
2
4
6
8
10
12
14
16
18
SNR (dB)
Sum capacity (bps/HZ)
Sum capacity vs SNR
SLNR-PERTUBATED
USLNR-PA
MMSE
CSLNR
Copyright © 2013 SciRes. CN