Circuits and Systems, 2013, 4, 472-477
Published Online November 2013 (http://www.scirp.org/journal/cs)
http://dx.doi.org/10.4236/cs.2013.47062
Open Access CS
Logical Function Decomposition Method for Synthesis of
Digital Logical System Implemented with Programmable
Logic Devices (PLD)
Mihai Grigore Timis, Alexandru Valachi, Alexandru Barleanu, Andrei Stan
Automatic Control and Computer Engineering Faculty, Technical University Gh.Asachi, Iasi, Romania
Received August 18, 2013; revised September 18, 2013; accepted September 26, 2013
Copyright © 2013 Mihai Grigore Timis et al. This is an open access article distributed under the Creative Commons Attribution Li-
cense, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
ABSTRACT
The paper consists in the use of some logical functions decomposition algorithms with application in the implementa-
tion of classical circuits like SSI, MSI and PLD. The decomposition methods use the Boolean matrix calculation. It is
calculated the implementation costs emphasizing the most economical solutions. One important aspect of serial de-
composition is the task of selecting “best candidate” variables for the G function. Decomposition is essentially a pro-
cess of substituting two or more input variables with a lesser number of new variables. This substitutes results in the
reduction of the number of rows in the truth table. Hence, we look for variables which are most likely to reduce the nu-
mber of rows in the truth table as a result of decomposition. Let us consider an input variable purposely avoiding all in-
ter-relationships among the input variables. The only available parameter to evaluate its activity is the number of “l”s or
“O”s that it has in the truth table. If the variable has only “1” s or “0” s, it is the “best candidate” for decomposition, as
it is practically redundant.
Keywords: Combinational Circuits; Static Hazard; Logic Design; Boolean Functions; Logical Decompositions
1. Introduction
In the implementation of logical functions we are looking
to optimize some parameters such as the propagation
time, cost, areas, power, etc. The decomposition problem
is old, and well understood when the function to be de-
composed is specified by a truth table, or has one output
only. However, modern design tools handle functions
with many outputs and represent them by cubes, for rea-
sons of efficiency. We develop a comprehensive theory
of serial decompositions for multiple-output, partially
specified, Boolean functions. A function

1,, n

f
xx

1,, r
u
has a serial decomposition if it can be expressed as
s
, where and
 
11
,,,,,
r
huu gvv

1,,

Uu
s
Vv v are subsets of the set

1,, n
X
xx
of input variables, and g and h have fewer inputvariables
than f.
It is sometimes the case that a set of Boolean functions
cannot be made to fit into any single module intended for
its implementation. The only solution is to decompose
the problem in such a way that the requirement can be
met by a network of two or more components each im-
plementing a part of the functions. The general pro-
blem can be stated as follows. The set of functions to be
implemented quires a logic block with N inputs and M
outputs. The decomposition task is to design a network
which will implement the function using blocks with a
maximum of n inputs and m outputs, where n < N or m <
M.
(A) Initially, we will consider a decomposition algo-
rithm of logical functions [1].
1.1. Given a Boolean function

110
,,,
n
f
xxx
 and
p Boolean functions denoted by


1 1100110
,,,,,,,,
pi i

y
yyy yy 
 
 
10
,,
p
, it is possi-
ble to decompose the function f depending on

? In other words, there is a function F so that



101 10
,,; ,,,,
pnin
F
zzfxx 
 
 
, where


10
,,
i
Yy y



1,, ni
and

Z
zz

 are disjoint
subsets of the set


10
,,
n
X
xx

, that means
X
YZ

 and YZ


 (1.1) (the empty set).
We will call this proceeding, Type I problem.
1.2. Given a Boolean function

110
,,,
n
f
xxx

there are q functions denoted by




0
,
1 110qi 0 11
,,,,,,,
i
y
yyy y 
 
 y and a
function F so that

M. G. TIMIS ET AL. 473



101 10
,,; ,,,,
qnin
F
zzfxx 
 
 

10
,,
i
Yy y



1,, ni
, where
and

Z
zz


 
210 1
,, 0,1,3,fxxx R

dec.echiv. 2
have the same
meaning as in 1.1. We will call this proceeding, the type
II problem.
(B) Matrices related to Boolean functions. The image
of a logical function [1]
It defines the image of a logical function the Boolean
row array that represents the values of this function, or-
dered by truth table.
For example, has the
following truth table:

5,7
x
1
x
0
x
f
0 0 0 0 1
1 0 0 1 1
2 0 1 0 0
3 0 1 1 1
4 1 0 0 0
5 1 0 1 1
6 1 1 0 0
7 1 1 1 1
Considering the above, we can write
11010101f (1.2)
We can verify the following properties:


121 2
1212
fff f

f
ff
 
 f
(1.3)
To a function can be attached a Veitch matrix, for the
previous case being:
210
\
1101
0101
x
xx
E 


(1.4)
2. The Representation of a Boolean Function
Using Subfunctions. The RJI Matrix
Let’s consider a function G of two subfunctions f1 and f0
that depend on the Boolean variables 210
,,
x
xx and on
the two variables 43 ,
x
x:

43100 4 314 310 4
,,,Gxxfff x xfx xffx (2.1)
After a simple calculation is deduced the image of
function G.
00000101110001 00G (2.2)
We suppose that the images of the two subfunctions
are:
1
0
01110100
01010011
f
f

 (2.3)
that means:
12110
02021
f
xx xx
f
xx xx




(2.4)
Starting from the expressions of G, f1 and f0 can be
calculated:


 
43210
431 2100210
4320 4321
4320431042
,,,,
,,,, ,,,
Fx xx xx
Gxxfxxxf xxx
xxxx xxxx
1
x
xxx xxxxxxx




(2.5)
The image of function F is calculated below:
00000000010100 111000101 100000011F

 (2.6)
The Veitch tables 43 10
:
x
xff
E

and 43 210
:
x
xxxx
E relating to
the G and F functions are:
43 1043210
\\
0000 00000000
0101 01010011
,
1100 10001011
0100 00000011
x
xffxxxxx
EE

 

 





 

 

 
(2.7)
Note that the E

matrix has only four distinct columns
that are found in E matrix.
In [1], it demonstrates that for the function F it can be
attached a pseudo-unitary matrix denoted by RJI in which
in each column the logic digit 1 corresponds to the E

column’s order number, therefore:
210
\
10001000
00000011
00100100
01010000
JI
x
xx
R








(2.8)
In [1] is also demonstrated the relation:
J
I
EE R


 (

—the matrix multiplication) (2.9)
Therefore, the decomposition of a function in subfu-
nctions is reduced to solving the following Boolean equa-
tions:
X
AB

 (2.10) (the type I problem, where the E
and RJI matrices are known) or
A
XB (2.11) (the
type II problem, where only the B matrix is known,
BE

).
Considering that the columns of matrix E' are found in
matrix E it deduces the matrix
A
E , and then the ma-
trix RJI.
Next, we present the solutions of the equations (2.10)
Open Access CS

M. G. TIMIS ET AL.
474
and (2.11), demonstrated in [1].
A. The solution of the equation
A
XB [1]
a) Let’s consider X a some matrix. It is valid the
relation (2.12), [1].
A
X
tB (tA-the transpose of the matrix A) (2.12)
b) Let’s consider X a pseudo-unitary matrix. It is valid
the relation (2.13) [1].
AA
X
tBtB (2.13)
B. The solution of the equation
X
AB [1]
a) Let’s consider A a some matrix. It is assumed [1]:
A
X
Bt (2.14)
b) Let’s consider A a pseudo-unitary matrix. It is
denoted by cA
X
Bt and aA
X
Bt. The suffi-
cient condition of existence of the solution [1] is:
and
cAaAc a
X
BtXBtXXX  (2.15)
If ca
X
X or ca
X
X, there is no solution for the
matrix X. In this case it is trying to solve the following
equations:



40
14310
1 43210
,,
,,,
,,,,
Fx x
Gxxff
H
xxxxx



(2.16)
(the previous solution) or



40
24310
2 43210
,,
,,,
,,,,
Fx x
Gxxff
H
xxxxx



(2.17)
(the consequence solution). We will return to these prob-
lems in a future paper.
3. Examples
(A) Let’s consider the function defined by


43210
1
,,,,
0,3,5,6,9,10,12,14,15,16,17,18,19,21, 22,30
Fx xx xx
R(3.1)
Applying the Veitch-Karnaugh method [2], a minimal
form is given by the expression:

4321043 210
3210 32104310
43204321 432
210 3210
,,,,Fxxxxxxxxxx
x
xxx xxxx xxxx
xxxxxxxx xxx
xxx xxxx

   


(3.2)
We define the cost of implementation as the number of
the inputs in the basic circuits, components [3]. In the
previous case, by implementing with AND-OR circuits,
results:




1564239 44CF . (It is consi-
dering that the input variables are provided inverted and
non-inverted, i.e. ,
ii
x
x.)
Let’s consider the following possible decomposition:


4310 43210
,,, ,,,,Gxxff Fxxxxx

where


11210
,,
f
fxxx,

00210
,,
f
fxxx.
For the function F corresponds the following Veitch
matrix, denoted by E:
10010110
01101011
11110110
00000010
E













(3.3)
Matrix E having four distinct columns, a solution for
E

is:
43 10
\
1001
0111
1101
0001
x
xff
E













(3.4)
Therefore, the matrix RJI, solution of the equation
JI
ER E


, is:
10010100
01100000
00001001
00000010
JI EE
Rt Et E










(3.5)
From where we obtain:
1
0
00001011
01100010
f
f


 (3.6)
or after an elementary calculation:


1210
01021
fxxx
0
f
xx xxx
 


(3.7)
Using E' matrix we obtain:
103 10430
430 143
Gffxffxxf
xxf fxx


 (3.8)
with a possible implementation as in Figure 1.
So, we will have:

 
10
7CfCf 8

 (3.9)




43 2519CG

 , so that

34CF

.
Open Access CS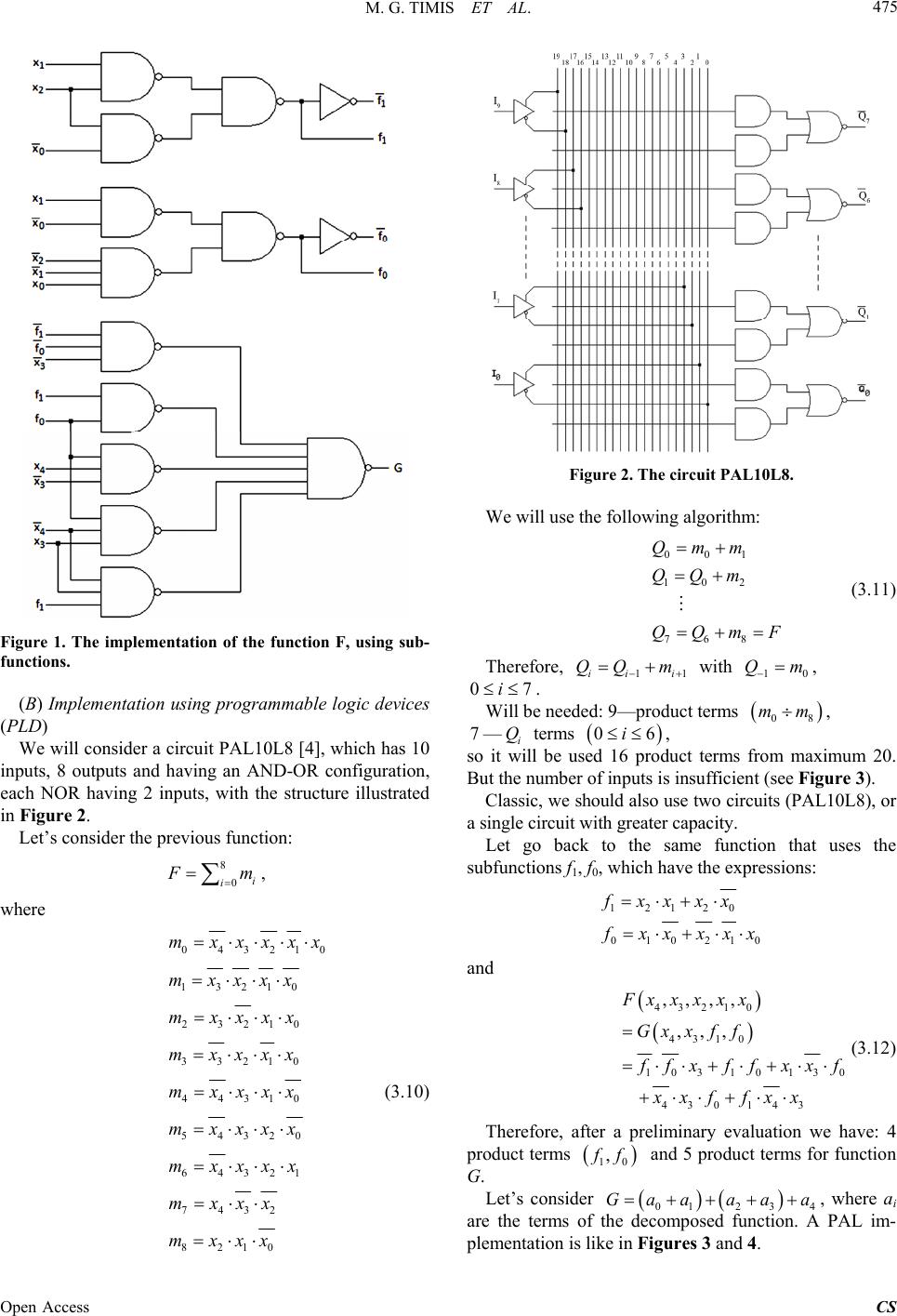

M. G. TIMIS ET AL. 475
Figure 1. The implementation of the function F, using sub-
functions.
(B) Implementation using programmable logic devices
(PLD)
We will consider a circuit PAL10L8 [4], which has 10
inputs, 8 outputs and having an AND-OR configuration,
each NOR having 2 inputs, with the structure illustrated
in Figure 2.
Let’s consider the previous function:
8
0i
i
F
m

,
where
0 43210
13210
23210
33210
44310
5 4320
6 4321
7432
8210
mxxxxx
mxxxx
mxxxx
mxxxx
mxxxx
mxxxx
mxxxx
mxxx
mxxx









(3.10)
Figure 2. The circuit PAL10L8.
We will use the following algorithm:
001
102
768
Qmm
QQm
QQmF



 (3.11)
Therefore, 1ii i
QQ m
1



 with ,
10
Qm

07i

.
Will be needed: 9—product terms ,

08
mm
7— i Q terms


06i

,
so it will be used 16 product terms from maximum 20.
But the number of inputs is insufficient (see Figure 3).
Classic, we should also use two circuits (PAL10L8), or
a single circuit with greater capacity.
Let go back to the same function that uses the
subfunctions f1, f0, which have the expressions:
12120
01021
fxxxx
0
f
xx xxx



and



43210
4310
103 10 130
430 143
,,,,
,,,
Fx xxxx
Gx xff
f
fxff xxf
xxf fxx




(3.12)
Therefore, after a preliminary evaluation we have: 4
product terms


10
,
f
f and 5 product terms for function
G.
Let’s consider

 
0123 4
Gaaaaa

 , where ai
are the terms of the decomposed function. A PAL im-
plementation is like in Figures 3 and 4.
Open Access CS

M. G. TIMIS ET AL.
476
Figure 3. PAL implementation.
Figure 4. A possible implementation of PAL10L8 circuit.
A possible implementation would be (see Figure 4):
4. Decomposition into EMB Blocks
The single step of the functional decomposition replaces
function F with two subfunctions [5]. This process is
recursively applied to both the G and H blocks until a
network is constructed where each block can be directly
implemented in single logic cell of target FPGA archi-
tecture.
Logic cell can implement any function of limited input
variables (typically 4 or 5). Thus the main effort of logic
synthesis methods based on decomposition is to find
such partition of input variables into free set and bound
set that allows creating decomposition with block G not
exceeding the size of logic cell. Various methods are
used, including exhaustive search since the size of logic
cell is small. It should be noted that the main constraint is
the number of inputs to block G and not the number of
outputs. This is because block G with more outputs than
in logic cell can be implemented with use of few logic
cells used in parallel. Since EMB blocks can be config-
ured to work as logic cell of many different sizes [6],
approach known from methods targeted for logic cells is
not efficient. The main reason is that the method must
check decomposition for many different sizes of block G.
The second factor is that in case of EMB the efficiency
of utilization of these blocks depends on carefully se-
lected size of block G. For example M512 RAM block of
Stratix device can be configured among others as 8 input
and 2 output logic cell or 7 input and 4 output logic cell.
Let assume that in decomposition search following solu-
tions are possible: block G with 8 inputs and 1 output or
block G with 7 inputs and 3 outputs. From the EMB
utilization point of view the second solution is better,
since it utilizes 384 bits of total 512 bits available, while
the first solution utilizes only 256 bits. R-admissibility is
used to evaluate serial decomposition possibilities for
different sizes of G block according to possible configu-
ration of EMB blocks. Since EMB can be configured as a
block of many different sizes the possible solution space
is large. Using Property 1 the search can be drastically
reduced. This will be explained in the following exam-
ple.
Example.
R-admissibility application to serial decomposition
evaluation. For function from Example 1 we have that
the admissibility of single input variables 16 ,,
x
x is
accordingly 4, 4, 4, 3, 3 and 4. This means that only for


4
Ux,


12 356
,,,,Vxxxxx and U,

5
x


,,xxxx
12346 decomposition with 2 outputs
from block G may exist.
,,V x
When considering solutions with 4 inputs to block G,
according to Property 1, [7,8] only solution with


45
,Uxx,


12 3 6
,,,Vxxxx should be evaluated.
We have:


 





45
45 452
or 48;16;23;57
2 or 2log23
xx F
xxxx F
re
 
 


 
(4.1)
This means that for such variable partitioning decom-
position may exist with block G having 1 output. With
this approach to serial decomposition, there is no differ-
ence between disjoint and non-disjoint decomposition in
their calculation. Particularly, it can be concluded that for
finding blanket G we can simply apply the method of
calculating compatible classes of βV blocks [7] which
was recently improved in [8].
Open Access CS

M. G. TIMIS ET AL.
Open Access CS
477
5. Conclusions
The paper represents the “rediscovery” of some decom-
position algorithms of Boolean logic functions, using sub-
functions [1].
After a brief exposure of the decomposition methods
of Boolean logical functions, the authors, through the
proposed example, shows the reduction of the implemen-
tation cost using standard logical circuits.
The authors show that when using PLD circuits, the
use of Boolean functions decomposition method reduces
the number of circuits necessary for the implementation
(see PAL10L8).
Balanced decomposition proved to be very useful in
implementation of combinational functions using logic
cell resources of FPGA architectures. However, results
presented in this paper show that functional decomposi-
tion can be efficiently and effectively applied also to im-
plement digital systems in embedded memory blocks.
Application of r-admissibility concept makes possible fast
evaluation of decompositions for different sizes of block
G. This allows selecting best possible decomposition stra-
tegy.
The paper showed that the use of Boolean functions
decomposition method reduces the number of circuits ne-
cessary for the implementation. However, this substitu-
tion process reduces the circuits cost by increasing the
circuit complexity, which also enhances the likelihood of
errors in the circuit design.
Balanced decomposition proved to be very useful in
implementation of combinational functions using logic
cell resources of FPGA architectures. However, results
presented in this paper show that functional decomposi-
tion can be efficiently and effectively applied also to im-
plement digital systems in embedded memory blocks.
REFERENCES
[1] M. Denouette, J. P. Perrin and E. Daclin, “Systemès Lo-
giques,” Tome I, Dunod, Paris, 1967, pp. 4-56.
[2] C. H. Roth, “Fundamentals of Logic Design,” West Pub-
lishing Company, Eagan, 1999, pp. 148-172.
[3] Al. Valachi, Fl. Hoza, V. Onofrei and R. Silion, “Analiza,
Sinteza şi Testarea Dispozitivelor Numerice,” Nord-Est,
1993, pp. 31-32; 45-53.
[4] J. A. Brzozowski and T. Łuba, “Decomposition of Boo-
lean Functions Specified by Cubes,” Journal of Multi-
ple-Valued Logic and Soft Computing, Vol. 9, 2003.
[5] M. Rawski, “Decomposition of Boolean Function Sets,”
Electronics and Telecommunications Quarterly, Vol. 53,
No. 3, 2007, pp. 231-249.
[6] J. A. Brzozowski and T. Łuba, “Logic Decomposition
Aimed at Programmable Cell Arrays,” International Con-
ference of Microelectronics: Microelectronics, Vol. 1783,
1992, pp. 77-88. http://dx.doi.org/10.1117/12.130993
[7] S. J. E. Wilton, “SMAP: Heterogeneous Technology
Mapping for Area Reduction in FPGAs with Embedded
Memory Arrays,” FPGA, 1998, pp. 171-178.
[8] “Logic Synthesis Strategy for FPGAs with Embedded Me-
mory Blocks,” Mariusz Rawski, Grzegorz Borowik, Ta-
deusz Łuba, Paweł Tomaszewicz, Bogdan j. Falkow- ski.
Przegląd Elektrotechnic Znyelectrical Review), R. 86 NR
11a/2010.