Communications and Network, 2013, 5, 150-155
http://dx.doi.org/10.4236/cn.2013.53B2029 Published Online September 2013 (http://www.scirp.org/journal/cn)
Adaptive Rate Control for Multi-Antenna Multicast in
OFDM Systems*
Qinghe Du1,2, Pinyi Ren1, Yi Jia1, Zhigang Chen1
1School of Electronic and Information Engineering, Xi’an Jiaotong University, China
2National Mobile Communications Research Laboratory of Southeast University, China
Received May, 2013
ABSTRACT
We propose two rate control sch emes for multi-antenna multicast in OFDM systems, which aim to maximize the mini-
mum average rate over all users in a multicast group. In our system, we do not require all multicast users to successfully
recover the signals received on each subcarrier. In contrast, we allow certain loss for multicast users, such that the mul-
ticast transmission rate can be increased. We assume that the loss-repairing can be completed at upper protocol layers
via advanced fountain codes. Following this principle, we formulate the rate control problem via beamforming in
multi-antenna multicast to optimize the minimum achievable rate for all multicast users. While the computation com-
plexity to solve for the optimal beamformer is prohibitively high, we propose a suboptimal iterative rate control scheme.
Moreover, we modify the above optimization problem by selecting a fixed proportion of users on each subcarrier. The
beamformer searching process will then be performed only based on the selected users on each subcarrier, such that the
complexity can be further reduced. We also solve this new problem with a low complexity approach. Theoretical
analyses and simulation results show that our proposed two rate control schemes can have higher minimum average rate
than the baseline scheme without rate control, while achieving low complexity.
Keywords: Multicast; OFDM; Multi-antenna; Rate Control
1. Introduction
Wireless multicast technology has received much atten-
tion in recent years and it is expected to have high de-
mand in the future [1-16]. It is very effective in spectru m
utilization, which lets the best statio n (BS) transmit same
message, e.g., video streaming and TV program, to mul-
tiple users simultaneously [1]. However, multiple users
want to receive the same message from the base station,
as a result, the achievable transmission rate is limited by
the weakest-link user in order to meet the needs of all
users [3]. So, resources are not fully utilized for the bet-
ter-link user. In order to use spectrum resource more
efficiently, there have been some studies on rate control
for multicast. In [4,5], P. K. Gopala proposed opportun-
istic multicast in TDMA system. The base station trans-
mits a fixed proportion of users who have better channel
gain on current time slot. That means a transmission rate
is decided which let only the proportion of users receive
signal successfully. However, the other users also need to
receive the signal; as a result, a lot of slots will be used
for retransmission of multicast signals. By the utilization
of fountain code technology, users who receive enough
bits of information within a period of time can decode
the signal successfully [6, 7]. As a result, users in multi-
cast system need not to be guaranteed that everyone de-
code signal on each slot successfully. Based on this, in [8,
9], opportunistic multicast schemes based on erasure
codes were proposed which select a subset of users to
transmit signal on each slot without retransmission. In [8],
T.-P. Low derived the optimal selection ratio that mini-
mizes the delay. Q. Le-Dang in [8] proposed the optimal
transmission rate and coding rate while using a
Reed-Solomon code RS (n, k). However, both [8] and [9]
didn’t consider fairness of users in multicast system. In
[10-13], the authors proposed a variety of multicast rate
control based on fairness. Among them, in [10], Q. Qu
proposed an opportunistic scheduling algorithm based on
fixed rate of FEC code and formulate a system through-
put maximization problem. In the problem, the constrains
are derived from every user’s specific minimum quality
of service (QoS) requirement. L. Tian in [11] proposed
*The research reported in this paper is supported by the National Natu-
ral Science Foundation of China under Grant No. 61102078, the Na-
tional Science and Technology Major Project under Grant No.
2010ZX03003-004-01, the Specialized Research Fund for the Doctoral
Program of Higher Education under Grant No. 20110201120014, the
Open Research Fund of National Mobile Communications Research
Laboratory, Southeast University (No.2011D10), and the Fundamental
Research Funds for the Central University.
C
opyright © 2013 SciRes. CN

Q. H. DU ET AL. 151
another rate control scheme based on QoS of users. Base
station chooses some good subcarriers to satisfy every
user’s QoS firstly, and then controls the transmission rate
to maximize the system throughput. Though authors of
[10] and [11] considered users’ QoS requirements, the
worst-link user in multicast system still get a low receiv-
ing rate. To be more fairness, authors in [12-14] pro-
posed to maximize the minimum rate of all multicast
users. In [12], U. C. Kozat proposed an objective to
maximize the minimum throughput capacity of all mul-
ticast users by a method which utilizes fixed-rate and
rateless erasure coding. W. Huang in [13] also consid-
ered the same objective, but algorithm in [14] was not
restricted to use a fixed selection ratio. In [14], unlike [12]
and [13], K. Bakanoglu studied the situation in OFDM
system. However, authors in [12-14] only consider that
BS has only one antenna, we need to study the situation
of multi-antennas.
Multi-antenna technology in multicast system has b een
studied for years. Most work in the literatures on
multi-antenna multicast focused on the max-min-fair
transmit beamforming proposed by N. Sidiropoulos in
[15]. Because Multicast system is limited to the
worst-link user, the BS utilizes available channel state
information (CSI) to generate a beamforming vector that
maximizes the minimum SNR among all users which
means we can get a maximum transmission rate. J. Xu in
[16] used the beamforming method of [15] on resource
allocation of multicast. However, J. Xu considers that all
the users will be chosen to control the transmission rate.
Because beamforming in multicast system may change
user’s receiving ability, which means some users may
have low rates even if their channel gains are not bad.
This is different with the tradition single-antenna multi-
cast system, and it makes it very difficult to utilize the
existing rate control algorithms.
In this paper, we propose two rate control schemes of
multi-antenna multicast in OFDM system. We firstly
formulate a rate control problem of multi-antenna multi-
cast which utilizes the max-min-fair transmit beamform-
ing in [15], and then propose a suboptimal solution based
on iteration. To reduce the complexity much lower, we
then simplify the system model by adding a constraint
that select a fixed proportion of u sers on each subcarrier.
After that we present a sub-optimal rate control to solve
the new optimization model. At last, theoretical analysis
and simulation are presented for the two rate control
schemes.
The rest of the paper is organized as follows. We first
introduce the system model in the next Section. Then in
Section 3 the proposed sch emes are presented . In Section
4, we present the Iteration convergence performance and
algorithmic complexity analysis. Some simulations are
shown in Section 5 to support our idea and finally the
conclusion of this paper is given in Section 6.
2. System Model
We consider a downlink scenario in which a BS (base
station) has an antenna array composed of T anten n a s and
M single-antenna users, as illustrated in Figure 1. There
are N subcarriers assigned to multicast services and the
bandwidth for each subcarrier is B. The power allocated
to subcarrier n is P. In the paper, (X)
H
, and
denote the Hermitian transpose, absolute value and ex-
pectation of a vector or matrixX, respectively.
[X]E
On subcarrier k, 1kK

, let , denotes hik 1N

downlink channel vector of user i. Assume multicast
signal is x and the beamforming vector of signal x is k.
Then the signal received at user i on subcarrier k can be
written as
w
,,
wh
H
ikk ikk
rP xn

 (1)
where k is the complex additive white Gaussian noise
with zero mean and variance .
n
0
From equation (1), we know the multicast signal’s
SNR of user i on subcarrier k is
N
2
,,
wh /
H
ikk ik
SNR N0 (2)
Let ,ik

denotes whether useris chosen on subcar-
rier k, and
i
,ik

is
,
,
1,user is chosen on subcarri er
0,user is chosen on subcarrier
ik
ik
ik
ik







 (3)
Let k
A
denotes set of multicast users chosen to
transmit signals on subcarrier k, 1k
A
M. From
equation (3) we can get
,
{|1,1, 2,...,}
kik
A
iiM


 (4)
Figure 1. System model for m ulticast transmissions.

Q. H. DU ET AL.
152
We use the method in [15] to calculate beamforming
vector , which is used to maximize the minimum
receiving SNR. The problem can be written as
wk
,
w
2
,
max min
.. w
{0,1}; 1,2,...,; 1,2,...,
k kik
iA
k
ik
SNR
st P
kKi 


  M
(5)
,
{|1,1,2,...,}, 1,2,...,
kik
A
iiMkK


Solving the equation (5), we can get the beamforming
vector , . Then we know the transmission
rate on subcarrier k is
wk1kK



*
2*,
*
log1min,
ki
i
rBSNR iA 
kk
M
r
r


(6)
So, the average rate of user i on all OFDM subcarriers
is
,
1/ ,1,2,...,
N
iikk
n
RqrNi


 (7)
where


,2,
,2,
1,log 1
0,log 1
ikik k
ikik k
qB SNR
qBSNR





(8)
In this paper, as illustrated in Figure 2, the transmitter
decides users who decode signal on each subcarrier suc-
cessfully by the perfect CSI information from all users.
Once the user set on subcarrier k is determined, we can
get the beamforming vector by equation (5), and then the
ransmission rate is got from equation (6).
Our objective is to maximize the minimum average
rate of all multicast users. According to the above analy-
sis, the optimization problem to be solved in this paper
can be mathematically formulated as follows:
,
,
max min
..{0,1}; 1,2,...,;1,2,...,
ik i
i
ik
R
s
tkKi

  M
(9)
Figure 2. Framework of rate control for multi-antenna
multicast.
3. Rate Control for Multi-Antenna
Multicast
There is only one optimization varialbe in equation (9),
which is the matrix

. From (3), we know that the op-
timal solution involves evaluating all 2
M
K possible user
selection combinations, and the one which maximize the
minimum average rate is the optimal solution. For the
high complexity of the brute-force method, in this section,
we present a suboptimal solution by iteration. Then we
simplify the optimal model by adding a constraint which
selects a fixed proportion of users on each subcarrier, in
order to have much lower complexity. After that we pre-
sent a low complexity method to solve the new optimiza-
tion model.
3.1. Iterative-Based Suboptimal Rate Control
In this section, subcarriers are allocated to users in an
iteration fashion. In each iteration, user who has the least
rate is chosen and BS allocates a best subcarrier to that
user. The suboptimal rate control can be described as
follows:
1) Initialization: Calculate the beamforming vector wk
on subcarrier k, ,kK1

 by equation (5), when
,ik M1,{1, 2,..i.,}


 , which means all the users are
chosen to transmit on subcarrier k. Calculate the capacity
of user i, where 1,iM

on subcarrier k by
,2
log (1)
ik ik
RB SNR
,

.
Choose the user i which maximize , that is
Let ,ik
R
,ˆ
ˆargmax .
nk
iR,ˆ
1,{ }.
k
ik
A
i  
2) Find useri

whose rate is minimum, argmin .
i
iR

If ,0,
ik



calculate the minimum rate denoted by
min
(,ik
R)

 on subcarrier k

when ,1.
ik


 Choose sub-
carrier on which the addition rate of minimum rate
is maximum through
*
k


*(,)
min ,
argmax .
ik ik
k
kR



R
We then denote the additional rate by .
*
k
R 
If *0,
k
R


or ,1,
ik


for {1, 2,..., },iM
{1,2,..., },kK

 the algorithm terminates. Or let
**
,1,{ }, ik kk
A
Ai

 


and back to step 2).
3.2. Sub-optimal Rate Control Based on Fixed
Proportion of Users
Rate Control based on iteration needs many times of it-
eration operation, each of which calculate once beam-
forming problem. So it still has a high complexity. In this
section, we propose to consider the situation that base
station chooses fixed proportion of users on each subcar-
rier to reduce complexity.

Q. H. DU ET AL. 153
We suppose that the fixed proportion is

, where
,
1
1, M
ik
i
M



and which means on subcarrier k, base
station choose
1,2,..., ,kK
M

users to calculate beamforming
vector and to determine the transmission rate.
According to the above analysis, the simplified opti-
mization problem of rate control for multicast can be
written as follows:
,
,,
1
max min
..{0,1};
1,2,..., ;1,2,...,
ik i
i
M
ik ik
i
R
s
t
kKiM

M






(10)
To solve the rate control problem above, which con-
tains
1
K
K
k
MM
MM







possible user selection choices. So the optimal solution is
brute-force method which has high complexity. For the
use in the practical system, we proposed a suboptimal
solution to equation (10). The suboptimal rate control can
be described as
1) Initialization: Choose 1/




 subcarriers ran-
domly, denoted by

/(1), (2),...,1




. On subcar-
rier ()n

, where 11/,n




BS chooses user
1M(1)n,

 M( 1)2nM,...,n


n
 , to transmit. On
subcarrier

1/ , 


use (1) 1M



1)nM M
( 2,...,


are chosen. Let these 1/



(1), ( 
U
subcarriers are used bands,
denoted byand let
.
 
2),..., 1/,
used
U   

..., }UK{1,2,
unuse used
2) Calculate all multicast users’ minimum average rate
by
,
1,1,2,...,
used
iikk
kU
used
Rqri
U

M
and sort them such that (1)(2)( ) ...
tt t
RR R
M

 . Choose
the least
M

users, who are user (1),(2),...,tt ( ).tM

After that, on unused subcarrier n, for unuse
where kn
 ,kU
1,2,n()
n
k
R..., U,(1),(2),..., ()tt tM
unuse calculate the minimum aver-
age rate when user

are cho-
sen on subcarrier .
n Then select the subcarrier which
maximize the minimum average rate, let it be band
Let
k
)
.
(
*arg n
k
maxkR
*
{}; {}.
usedusedunuse unuse
UUkU Uk 
*
3) If ,
unuse which means there still has some
subcarriers unused. So back to step 2). Or the algorithm
terminates.
U
If the base station use the suboptimal rate control
based on fixed proportion of users, it needs to know the
value of .

Different

will get different minimum
rate. When 1


, all users are chosen to transmit on all
subcarriers, implying that rate control is not employed.
However, due to the calculation method of beamforming
vector in [15], we cannot get a closed formulation of

.
Here we propose a simply method to get a good

.
We sample different

for L times uniformly and
calculate the corresponding minimum average rate. Be-
cause the fixed proportion of users in multicast system
which is denoted by

,

1/ ,2/ ,,/,
M
MMM 
has limited possible value, we sample


*12
, ,...,,
L
 


//,1
llM LMlL
 .
,
Then, calculate the corresponding minimum rate
()
min ,
l
R
1lL

 and choose the value

that maximize the
minimum rate, which can be written as
()
min
argmax .
l
l
R

 
4. Performance Analyses
4.1. Iteration Convergence
In the optimal question of rate control based on iteration,
there is only one variable

which is a
M
K matrix
and the value in it is either 0 or 1. So there is only 2
M
K
possible value for matrix

. In the suboptimal rate con-
trol based on iteration, at each iteration, the user who has
the least rate is chosen, and we find a best subcarrier to
that user. In the extremely bad situation, the maximum
number o f iteration is g iv en by
1
1
1
() (1
2
K
nMK nMKK

).



Therefore, the suboptimal approach is convergent.
4.2. Computational Complexity
From the above section, we know the maximum number
of iteration is (1)/2MK K,

in the suboptimal rate
control algorithm based on iteration. Then the complex-
ity of it is . In the suboptimal rate control
based on fixed proportion of users, th e base station n eeds
total
2
()OMK

 
1
1/ ()1/1/1 /2
K
nKn KK 



  
 
 

times of beamforming operations when

is deter-
mined, so the complexity is . As a result, the
method used to get
2
()OK

in this paper needs to calculate
different L

times, each of which has complexity of
. So the complexity of the suboptimal rate control
based on fixed proportion users is . Because
there are only M possible values of
2
()OK 2
K(OL )

, we know that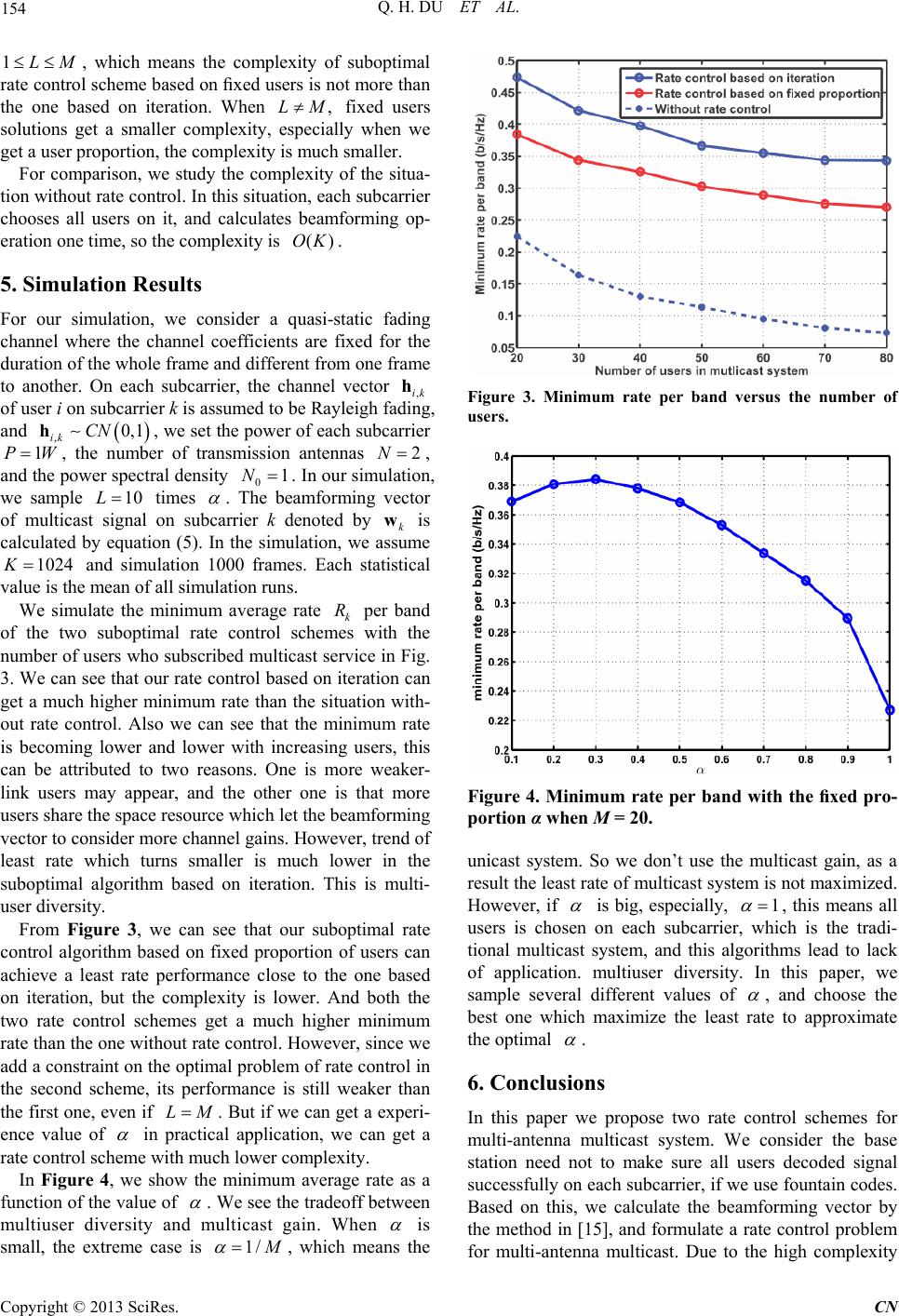

Q. H. DU ET AL.
154
1LM
,ik h
1PW
, which means the complexity of suboptimal
rate control scheme based on fixed users is not more than
the one based on iteration. When fixed users
solutions get a smaller complexity, especially when we
get a user proportion, the complexity is much smaller.
,LM
()OK
For comparison, we study the complexity of the situa-
tion without rate control. In this situation, each subcarrier
chooses all users on it, and calculates beamforming op-
eration one time, so the complexity is .
5. Simulation Results
For our simulation, we consider a quasi-static fading
channel where the channel coefficients are fixed for the
duration of the whole frame and different from one frame
to another. On each subcarrier, the channel vector ,ik
of user i on subcarrier k is assumed to be Rayleigh fading,
and , we set the power of each subcarrier
, the number of transmission antennas
h
2

0,1CN N

,
and the power spectral density 0. In our simulation,
we sample times 1N
10L

. The beamforming vector
of multicast signal on subcarrier k denoted by k is
calculated by equation (5). In the simulation, we assume
and simulation 1000 frames. Each statistical
value is the mean of all simulation runs.
w
1024K
We simulate the minimum average rate k per band
of the two suboptimal rate control schemes with the
number of users who subscribed multicast service in Fig.
3. We can see that our rate control based on iteration can
get a much higher minimum rate than the situation with-
out rate control. Also we can see that the minimum rate
is becoming lower and lower with increasing users, this
can be attributed to two reasons. One is more weaker-
link users may appear, and the other one is that more
users share the space resource which let the beamforming
vector to consider more channel gains. However, trend of
least rate which turns smaller is much lower in the
suboptimal algorithm based on iteration. This is multi-
user diversity.
R
From Figure 3, we can see that our suboptimal rate
control algorithm based on fixed proportion of users can
achieve a least rate performance close to the one based
on iteration, but the complexity is lower. And both the
two rate control schemes get a much higher minimum
rate than the one without rate control. However, since we
add a constr aint on the optimal prob lem of rate control in
the second scheme, its performance is still weaker than
the first one, even if . But if we can get a experi-
ence value of LM

in practical application, we can get a
rate control scheme with much lower complexity.
In Figure 4, we show the minimum average rate as a
function of the value of

. We see the tradeoff between
multiuser diversity and multicast gain. When

is
small, the extreme case is 1/
M


, which means the
Figure 3. Minimum rate per band versus the number of
users.
Figure 4. Minimum rate per band with the fixed pro-
portion α when M = 20.
unicast system. So we don’t use the multicast gain, as a
result the least rate of multicast system is not maximized.
However, if

is big, especially, 1

, this means all
users is chosen on each subcarrier, which is the tradi-
tional multicast system, and this algorithms lead to lack
of application. multiuser diversity. In this paper, we
sample several different values of

, and choose the
best one which maximize the least rate to approximate
the optimal

.
6. Conclusions
In this paper we propose two rate control schemes for
multi-antenna multicast system. We consider the base
station need not to make sure all users decoded signal
successfully on each subcarrier, if we use fountain codes.
Based on this, we calculate the beamforming vector by
the method in [15], and formulate a rate control problem
for multi-antenna multicast. Due to the high complexity

Q. H. DU ET AL.
155
of the brute-force method, we firstly study a suboptimal
rate control method by iteration. After that, we add a
constraint of choosing fixed proportion users on the op-
timal problem, and study a suboptimal solution of it. In
addition, we present performance analysis of iteration
convergency and complexity. Simulation results indicate
that our schemes can get much better minimum rate than
the situation without rate control.
REFERENCES
[1] F. Hartung, U. Horn, J. Huschke, M. Kampmann, T.
Lohmar and M.Lundevall, “Delivery of Broadcast Ser-
vices in 3G Networks,” IEEE Transactions Broadcasting,
Vol. 53, No. 1, 2007, pp. 188-199.
doi:10.1109/TBC.2007.891711
[2] Q. Du and X. Zhang, “Statistical QoS Provisionings for
Wireless Unicast/Multicast of Multi-Layer Video
Streams,” IEEE Journal of Selected Areas in Communi-
cations, Vol. 28, No. 3, 2010, pp. 420-433.
doi:10.1109/JSAC.2010.100413
[3] N. Jindal and Z.-Q. Luo, “Capacity Limits of Multiple
Antenna Multicast,” in Proc. IEEE International Sympo-
sium on Information Theory, Seattle, USA, 2006, pp.
1841-1845.
[4] P. K. Gopala and H. E. Gamal, “Opportunistic Multicast-
ing,” in Proc. IEEE Thirty-Eighth Asilomar Conference
on Signals, Systems and Computers, Pacific Grove, CA,
2004, pp. 845-849.
[5] Gopala, Praveen Kumar; El Gamal, H., “On the Through-
put-delay Tradeoff in Cellular Multicast,” in Proc. Inter-
national Conference on Wireless Networks, Communica-
tions and Mobile Computing, Maui, Hi, 2005, pp.
1401-1406.
[6] M. Luby, M. Watson, T. Ga siba, T. Stockhammer and W.
Xu, “Raptor Codes for Reliable Download Delivery in
Wireless Broadcast Systems,” in Proc. the 3rd IEEE
Consumer Communications and Networking Conference,
Las Vegas, NV, Jan. 2006, pp. 192-197.
[7] fD. J. C. MacKay, “Fountain Codes,” IEEE Proceed-
ings-Communications, Vol. 152, 2005, pp. 1062- 1068.
[8] T.-P. Low, M. on Pun, Y.-W. Hong and C.-C. Kuo, “Op-
timized Opportunistic Multicast Scheduling (oms) over
Wireless Cellular Networks,” IEEE Transactions Wire-
less Communications, Vol. 9, No. 2, 2010, pp. 791-801.
http://dx.doi.org/10.1109/TWC.2010.02.090387
[9] Q. Le-Dang, T. Le-Ngoc and Q. Ho, “Opportunistic Mul-
ticast Scheduling with Erasure-Correction Coding over
Wireless Channels,” in proc. IEEE ICC 2010, Cape Town,
South Africa, 2010, pp. 1-5.
[10] Q. Qu and U. Kozat, “On the Opportunistic Multicasting
in Ofdm-based Cellular Networks,” in proc. IEEE ICC
2008, Beijing, China, 2008, pp. 3708-3714.
[11] L. Tian, D. Pang, Y. B. Yang and D. Eryk, “Subcarrier
Allocation for Multicast Services in Multicarrier Wireless
Systems with QoS Guarantees,” in Proc. IEEE WCNC
2010, Sydney, Australia, 2010, pp. 1-6.
[12] U. C. Kozat, “On the Throughput Capacity of Opportun-
istic Multicasting with Erasure Codes,” in Proc. IEEE
INFOCOM, Phoenix, AZ, May 2008, pp. 520-528.
[13] W. Huang and K. L. Yeung, “On Maximizing the
Throughput of Opportunistic Multicast in Wireless Cel-
lular Networks with Erasure Codes,” in Proc. IEEE ICC
2011, Kyoto, Japan, Jun. 2011, pp. 1-5.
[14] K. Bakanoglu, M. Wu, H. Liu and M. Saurabh, “Adaptive
Resource Allocation in Multicast OFDMA Systems,” in
Proc. IEEE WCNC 2010, Sydney, Australia, 2010,
pp.1-6.
[15] N. Sidiropoulos, T. Davidson and Z.-Q. Luo, “Transmit
Beamforming for Physical-layer Multicasting,” IEEE
Transactions Signal Process., Vol. 54, No. 6, 2006, pp.
2239-2251. doi:10.1109/TSP.2006.872578
[16] J. Xu, S. Lee, W. Kang and J. Seo, “Adaptive Resource
Allocation for MIMO-OFDM Based Wireless Multicast
Systems,” IEEE Trans. BROADCASTING, Vol. 56, No. 1,
2010, pp. 98-102. doi:10.1109/TBC.2009.2039691