Communications and Network, 2013, 5, 127-131
http://dx.doi.org/10.4236/cn.2013.53B2024 Published Online September 2013 (http://www.scirp.org/journal/cn)
Partial Feedback Based Orthogonal Space-Time Block
Coding With Flexible Feedback Bits*
Lei Wang, Zhigang Chen
School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an, China
Received June, 2013
ABSTRACT
The conventional orthogonal space-time block code (OSTBC) with limited feedback has fixed feedback bits for
the specific transmit antennas. A new partial feedback based OSTBC which provides flexible feedback bits is
proposed in this paper. The proposed scheme inherits the properties of having a simple decoder and the full diversity of
OSTBC, moreover, preserves full data rate. Simulation results show that for transmit antennas, the proposed
scheme has the similar performance with the conventional one by using
1p
T
np
T
np
1p

feedback bits, whereas has the better
performance with more feedback bits.
Keywords: MIMO; Transmit Diversity; Space-time Block Coding; Parti a l Feed b ack
1. Introduction
Orthogonal space-time block coding (OSTBC) is a sim-
ple and effective transmission paradigm for MIMO sys-
tem, due to achieving full diversity with low complexity
[1]. One of the most effective OSTBC schemes is the
Alamouti code [2] for two transmit antennas, which has
been adopted as the open-loop transmit diversity scheme
by current 3GPP standards. However, the Alamouti code
is the only rate-one OSTBC scheme [3]. With higher
number of transmit antennas, the OSTBC for complex
constellations will suffer the rate loss.
Focusing on this drawback, the open-loop solutions
have been presented, such as the quasi-OSTBC (QOS-
TBC) [4] with rate one for four transmit antennas, and
other STBC schemes [5,6] with full rate and full diver-
sity. Alternatively, the close-loop solutions have also
been designed to improve the performance of OSTBC by
exploiting limited channel information feedback at the
transmitter. In this paper, we focus on the close-loop
scheme.
Based the group-coherent code, the bits feed-
back based OSTBC for T transmit antennas has been
constructed in [7], and generalized to an arbitrary number
of receive antennas in [8]. The partial feedback based
schemes in [7,8] exhibit a higher diversity order while
preserving low decoding complexity. However, these
schemes for transmit antennas require a fixed
number of
1p
np
T
np
1p

bits feedback. That is to say, for such
scheme, improving the performance by increasing the
feedback bits implies that the number of transmit anten-
nas T must be increased at the same time. Therefore,
the scheme is inflexible in compromising the perform-
ance and the feedback overhead.
np
In this paper, by multiplying a well-designed feedb ack
vector to each signal to be transmitted from each antenna,
we propose a novel partial feedback based OSTBC
scheme with flexible feedback bits. In this scheme, the
OSTBC can be straightly extended to more than two an-
tennas. Importantly, we can show that the proposed
scheme preserves the simple decoding structure of OS-
TBC, full diversity and full data rate.
Notations: Throughout this paper,

and
T


H

represent “transpose” and “Hermition”, respectively.


aRe denotes the real part of a complex , and a
1j

.
2. Proposed Code Construction and System
Model
Consider a MIMO system with transmit and
T
np
R
n
n
G
receive antennas. Assuming we have an OSTBC T
for transmit antennas, and can be denoted as
T
nT
n
G
12
T
nT n





c cGc, where is the
m
c1T

sig-
*This work was supported by the National Natural Science Foundation
of China under Grant 60902045, the International Cooperation Projects
of China-Finland under Grant 2010DFB10570, and the National Sci-
ence & Technology Major Projects of China under Grant 2010ZX-
03003-004.
C
opyright © 2013 SciRes. CN

L. WANG, Z. G. CHEN
128
nal to be transmitted from the mth antenna for
. Then a code to be transmitted from T
antennas, where is an integer, may be con-
structed as
1,, T mn
l
m
np
2p
1
T
T
n
l
npm m
m
 Gcβ (1)
where is the 1T feedback vector for the th
antenna, which is defined as , where
l
m
βnpll
mm
βφb

denotes the Kronecker product, m is the th row of
the identity matrix , and φm
p
T
n
I1

vector is given by
l
b
  1
12
2
:1 p
jQb
jQb
lee




 b (2)
where . For the feedback
vector at the mth antenna, it contains a subset of all pos-
sible

11
,,0,1,, 1
p
bb AQ
 
1

p
Ql
m
β feedback vectors , i.e., 1 1, 2,,
p
lQ

.
With the transmission of T
Tnp

code matrix T
np
G,
the
l
R
Tn receive signal can be
written as 1,,R
n


y


Yy
T
l
np
YG HN
(3)
where is the channel ma-
trix, and is the
1,,R n

 Hhh
1,,R n

 Nnn
T
np nR
R
Tn
H
complex Gaus-
sian noise matrix. The entries of and are inde-
pendent samples of a zero-mean complex Gaussian ran-
dom variable with variance 1 and
N
T
np

respectively,
where

is the average signal-to-noise ratio (SNR) at
each receive antenna.
3. Linear Decoder at the Receiver
The received signal at ith receive antenna can be re-
written as
TT
T
ll
inpiini
l
ni i



y Ghn GBhn
Gh n
i
(4)
where the TT
matrix is composed of T
feedback vectors, and can be expressed in a stacked form
given by
nnpl Bn
 
1T
T
T T
ll l
n



Bββ
.
We divide channel vector into seg-
ments in the following way
1
T
npi hT n
1
,1,,(1) 1,
::
,, ,,,,
TT
TT
iinT
T
ii ipinpipn
hh hh








 
gg
h


(5)
where each segment can be denoted as (
ik
g1,, T kn

)
with dimension . Then the equivalent channel vec-
tor in (4) has the form of
1p
ll
i


hBh
i
i
 
1
12
T
T
T
ll l
iin
T
ll l
ii in


 






φbh φbh
bg bgbg


h
i
y
(6)
For convenience, we will use th e Alamouti code as the
basic OSTBC matrix T
n in the rest of this paper, and
the results can be straightly extended to other OSTBC.
For the received signal in (4), After performing the con-
jugate operation to the second entry of , the received
signal can be equivalently expressed as
G
i
y
l
ii i

  yRxn (7)
where is the equivalent channel matrix correspond-
ing to the entries of and their conjugates, and
l
i
R

12
T
l
i

h

s
sx has a pair of symbols in the Alamouti
code. Denote the kth entry of as , and ac-
cording to the linearity of th e OSTBC [9], the equivalent
channel matrix has the form of
l
i

h

l
ik

h
l
i
R
2
 

*
1
ll l
ikiki
k
kk









RChDh (8)
where the matrices k and k
D specifying the Alamouti
code are defined in [9]. Since matched filtering is the
first step in the detection process, left-multiplying by
C
i
 y

H
l
i
Rwill yield


HH
lll
iiii i

 
rR

i
y
MxRn (9)
where . Due to the properties of
and for the Alamouti code, we get

H
ll
ii
R
l
i
MR
k
D
k
C
 



22
11
2
22
12
l
i
ll l
ii i
ll
ii

 



Mh h CD
hI I
(10)
where

denotes the equivalent channel gain for re-
ceive antenna i. It is clear that is a diagonal matrix,
therefore, the simple decoder of OSTBC can be straightly
applied for (7), thus
l
i
M
1
s
and 2
s
can be decoded inde-
pendently.
4. Feedback Bits Selection and Properties
In this section, we will discuss the feedback bits selection
criterion and the key properties of the proposed scheme.
4.1. Feedback Bits Selection
At the th receive antenna,
il
i

can be expressed in the
following quadratic form
2
222
12
1
ll llHl
iiiiikik
k


 


hbgbg gAg
(11)

L. WANG, Z. G. CHEN 129
where



1
1
11
1
11
1
1
1
:,
1
p
p
p
p
b
b
bb
b
H
lll
bb b
























Abb


and


2
j
Q
e

 .
For all the
R
n receive antennas, then the total chan-
nel gain is given by
21
111 , 1,2,,
RR
nn
ll Hl
iikik
iik
l 
p
Q


 
 gAg (12)
It is clea r that in orde r to im prove t he sy stem perform anc e,
we must feedback the specific l with bits,
which provides the largest (1)logpQ
l
l

. Denote the entry
of as , thus

,mn
l
Al
mn
A1
l
mm

A, and

11m
bb
n
l
mn




A,
where preset. Moreover, it is easy to verify
that nm . Then the quadratic form in (11) can
be represented as
0
b
mn A
0 is

l
A

*
l
 
 
*
11
1
2*
21, 2Re
pp
Hl l
ikikmn ikik
mn
pp l
ikik ikmn
mnnm
mn
mn





 


gAgA gg
gggA
l
(13)
where denotes the n element in , and

ik ngthik
g


,1
ik ik pn
nh

g.
Substituting (13) in (11) and 1
R
n
li
i


 leads to
 
1
2
2*
,1 ,1
1121,
:
2Re
R
npp
l l
mn ik pmik pn
Fikmnnm
hh



 



 
 

H

A
Q
(14)
Thus, the feedback bits will be selected
as (1)logp
1
argmax ,1,2,,
p
opt l
ll 

Q
l
(15)
In this way, we can choose the optimal feedback vec-
tor , further construct for the mth
transmit antenna.
l
bl
mm
βφb
4.2. Diversity Analysis
The key property of the proposed partial feedback based
OSTBC scheme is proved in the following.
Property 1: The partial feedback based OSTBC
in (1) can achieve full diversity.
T
Proof: For simplicity, we denote
l
np
G
1
p
LQ

. Selecting
the optimal will provide the largest channel gain
opt
l

1
max, ,

1
1
22
11111 1
1
max, ,
11
RR
L
Ll
l
nn
LL
HlHl
ik ikikik
likik l
L
LL
 

  






 

gAggA g
(16)
For the summed matrix , it is clear that its
1
Ll
l
A
diagonal elements equal to L, and its non-diagonal ele-
ments have the form of

11
11
1,0 ,1,
nm
nm
Lbb
l
mn
lmnbb Q
mn




 



A

1
(17)
Let 1nm
kb b



, since 0, (17) is re-
duced to 1kQ
1
1,0 0
Q
Llk
mn
lmn k


 


A (18)
Therefore, we can obtain 1
Ll
p
l
L


AI
, which can be
substituted into (16) and yields

222
12
1111
22
1
1
RR
R
nn
LlH
ik ikii
lik i
n
iF
i
L

 



 

ggg g
hH
(19)
Since the lower bound of the channel gain provides
full diversity of TR
, the proposed scheme can cer-
tainly guarantee the full diversity.
npn
4.3. Configuration of Flexible Feedback Bits
Furthermore, the proposed scheme has the flexi-
ble feedback bits. For a specific p, T has the feed-
back bits of
T
l
np
Gl
np
G
(1)logpQ

. However, for the number that
not equal to (1)logpQ

, we can rewrite the vector
l
b in (2) as


11
11 2
2
1pp
jQb
jQb
lee










b, thus
the number of feedback bits is . For example,
1
1
log p
i
i
Q



for 2
T
n

and 4p

, the number of feedback bits are
3 and 6 in the case of 2Q

, and , respectively.
If we set 12
4Q
2QQ

, and 3 Q in , then the
number of feedback bits is 4, and if we set 1
4l bQ2

, and
23
4QQ

 in , then the number of feedback bits is
5, and so on.
l
b
4.4. BER Analysis
Assuming the power of each smbol in y

12
T
s
sx is
normalized to unity, i.e.,

21
i
Es  for 1,2i

, we
can obtain the average SNR per bit has the form of

1
max, ,
2
L
bT
np


.

L

, which can be lower bounded by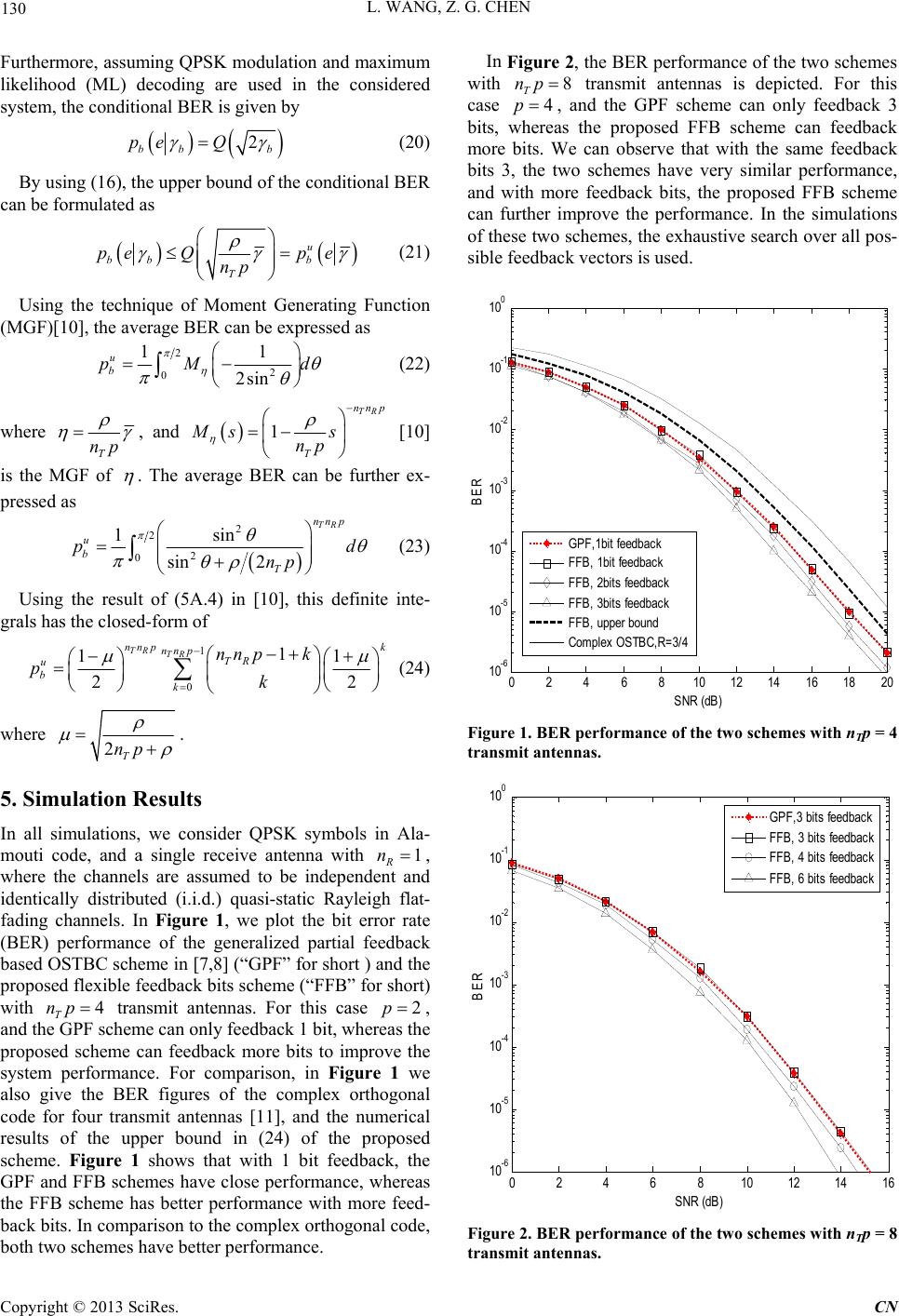

L. WANG, Z. G. CHEN
130
Furthermore, assuming QPSK modulation and maximum
likelihood (ML) decoding are used in the considered
system, the conditional BER is given by



2
bb b
pe Q

 (20)
By using (1 6), th e upp e r bound o f the cond itio n al BER
can be formulated as
 
u
bb b
T
pe Qpe
np










(21)
Using the technique of Moment Generating Function
(MGF)[10], the average BER can be expressed as
2
2
0
11
2sin
u
b
pM


d






 
(22)
where
T
np


, and

1
TR
nnp
T
Ms s
np







[10]
is the MGF of

. The average BER can be further ex-
pressed as

2
2
2
0
1sin
sin 2
TR
nnp
u
b
T
pd
np









 (23)
Using the result of (5A.4) in [10], this definite inte-
grals has the closed-form of
1
0
1
11
22
TR TR
nnp k
nnp TR
u
bk
nnp k
pk





 
 

 
 




(24)
where 2T
np



.
5. Simulation Results
In all simulations, we consider QPSK symbols in Ala-
mouti code, and a single receive antenna with 1
R
n

,
where the channels are assumed to be independent and
identically distributed (i.i.d.) quasi-static Rayleigh flat-
fading channels. In Figure 1, we plot the bit error rate
(BER) performance of the generalized partial feedback
based OSTBC scheme in [7,8] (“GPF” for short ) and the
proposed flexible feedback bits scheme (“FFB” for short)
with transmit antennas. For this case 4
T
np2p

,
and the GPF scheme can only feedback 1 bit, whereas the
proposed scheme can feedback more bits to improve the
system performance. For comparison, in Figure 1 we
also give the BER figures of the complex orthogonal
code for four transmit antennas [11], and the numerical
results of the upper bound in (24) of the proposed
scheme. Figure 1 shows that with 1 bit feedback, the
GPF and FFB schemes have close performance, whereas
the FFB scheme has better performance with more feed-
back bits. In comparison to the complex orthogonal code,
both two schemes have better performance.
In Figure 2, the BER performance of the two sch emes
with 8
T
np

transmit antennas is depicted. For this
case 4p

, and the GPF scheme can only feedback 3
bits, whereas the proposed FFB scheme can feedback
more bits. We can observe that with the same feedback
bits 3, the two schemes have very similar performance,
and with more feedback bits, the proposed FFB scheme
can further improve the performance. In the simulations
of these two schemes, the exhaustive search over all pos-
sible feedback vectors is used.
0 2 46810 12 1416 18 20
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
S NR (dB)
BER
GP F ,1 bi t feedback
FF B, 1bit feedbac k
FF B, 2bits feedback
FF B, 3bits feedback
FF B, upper bound
Com p l ex OS TB C,R=3 /4
Figure 1. BER performance of the two schemes with nTp = 4
transmit antennas.
0 2 4 6810 12 14 16
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
S NR (dB)
BER
GP F ,3 bits feedback
FF B, 3 bits feedback
FF B, 4 bits feedback
FF B, 6 bits feedback
Figure 2. BER performance of the two schemes with nTp = 8
transmit antennas.

L. WANG, Z. G. CHEN
131
6. Conclusions
In this paper, we proposed a partial feedback based
OSTBC scheme with flexible feedback bits. The new
scheme inherits the OSTBC properties of achieving full
diversity, preserving low decoding complexity, and has
full rate. Moreover, compared with the convention al par-
tial feedback based OSTBC schemes, the new scheme
can support flexible feedback bits and can improve the
system performance with more feedback bits.
REFERENCES
[1] V. Tarokh, H. Jafarkhani and A. R. Calderbank,
“Space-time Block Codes from Orthogonal Designs,”
IEEE Transactions on Information Theory, Vol. 45, No. 5,
1999, pp. 1456-1467.doi:10.1109/18.771146
[2] S. M. Alamouti, “A Simple Transmitter Diversity Scheme
for Wireless Communications,” IEEE Journal on Selected
Areas in Communications, Vol. 16, No. 8, 1998, pp.
1451-1458.doi:10.1109/49.730453
[3] S. Sandhu and A. J. Paulraj, “Space-time Block Codes: A
Capacity Perspective,” IEEE, Communications Letters,
Vol. 4, No. 12, 2000, pp. 384-386.
doi:10.1109/4234.898716
[4] H. Jafarkhani, “A Quasi-orthogonal Space-time Block
Code,” IEEE Transactions on Communications, Vol. 49,
No. 1, 2001, pp. 1-4. doi:10.1109/26.898239
[5] W. Su and X. G. Xia, “Signal Constellations for Quasi-
orthogonal Space-time Block Codes with Full Diversity,”
IEEE Transactions on Information Theory, Vol. 50, 2004,
pp. 2331-2347. doi:10.1109/TIT.2004.834740
[6] X. L. Ma and G. B. Giannakis, “Full-diversity Full-rate
Complex-field Space-time Coding,” IEEE Transactions
on Signal Processing, Vol. 51, No. 11, 2003, pp.
2917-2930.doi:10.1109/TSP.2003.818206
[7] J. Akhtar and D. Gesbert, “Extending Orthogonal Block
Codes with Partial Feedback,” IEEE Transactions on
Wireless Communications, Vol. 3, No. 6, 2004, pp.
1959-1962.doi:10.1109/TWC.2004.837469
[8] A. Sezgin, G. Altay and A. Paulraj, “Generalized Partial
Feedback Based Orthogonal Space-time Block Coding,”
IEEE Transactions on Wireless Communications, Vol. 8,
No. 6, 2009, pp. 2771-2775.
doi:10.1109/TWC.2009.080352
[9] B. Hassibi and B. M. Hochwald, “High-rate Codes That
Are Linear in Space and Time,” IEEE Transactions on
Information Theory, Vol. 48, No. 7, 2002, pp. 1804-1824.
doi:10.1109/TIT.2002.1013127
[10] M. K. Simon and M. S. Alouini, “Digital Communication
over Fading Channels,” John Wiley & Sons Inc., 2000.
[11] G. Ganeon and P. Stoica, “Space-time Block Codes: A
Maximum SNR Approach,” IEEE Transactions Informa-
tions Theory, Vol. 47, No. 4, 2001, pp. 1650-1656.
doi:10.1109/18.923754