 Communications and Network, 2013, 5, 119-126 http://dx.doi.org/10.4236/cn.2013.53B2023 Published Online September 2013 (http://www.scirp.org/journal/cn) One-User/One-Group Soft-Decision Aided Multiuser Detection for 2D Spread MC DS-CDMAs Hoang-Yang Lu, I-Hsuan Lai Dept. of Electrical Engineering, National Taiwan Ocean University. Email: hylu@mail.ntou.edu.tw, rockrice043@gmail.com Received June, 2013 ABSTRACT We consider the uplink of a multiuser, multiple-input multiple-output (MIMO), frequency-time-domain spread, multi- carrier (MC), direct sequence code division multiple access (DS-CDMA) system. As other CDMA-like systems, the multiple access interference (MAI) effect still exists in such an MC DS-CDMA system. To mitigate the MAI effect, we propose user-based and group-based layered detection schemes. Specifically, to enable a trade-off between the per- formance and the computational complexity, the schemes only use one user's/group's soft decisions for user-based/ group-based layered detection. The results of simulations demonstrate that the proposed schemes outperform existing approaches, and th eir computatio nal complexity is modest. Keywords: Multiuser detection, MC DS-CDMA, VBLAST, MIMO 1. Introduction The rapidly increasing demand for better quality of ser- vice (QoS) in wireless systems has motivated the devel- opment of several promising approaches to improve sys- tem capacity and transmission reliability. One promising multiple access approach for sharing valuable bandwidth resources is called multi-carrier (MC) direct sequence code division multiple access (DS-CDMA) [1,2]. Re- cently, a new MC scheme, called frequency-time-domain (FT-domain) spread MC DS-CDMA, was proposed in [3]. The scheme first spreads the transmitted symbol by a time-domain (T-domain) signature code. Then, the T- domain spreading signal is copied to each subcarrier to be spread by a frequency-domain (F-domain) signature code. In addition to providing the superior capacity per- formance gain, FT-domain spread MC DS-CDMA sys- tems have other attractive features, such as short and low-chip-rate signature codes for realizing low-rate sig- nal processing [4]. It has been shown that multiple-input multiple output (MIMO) systems, which deploy multiple antennas on the transmitter side and the receiver side, can yield a signifi- cant performance gain for wireless communications [5]. Spatial multiplexing (SM), one of the key MIMO tech- nologies [5], uses multiple transmit antennas in parallel to send multiple symbols to the receiver. In particular, to facilitate symbol detection in SM-based MIMO systems, an effective layered detection scheme, called Vertical Bell Laboratories Layered Space-Time (VBLAST), was proposed in [5,6]. Because of VBLAST's efficiency and feasibility, SM-based MIMO systems can provide high throughput, and they have motivated a considerable amount of research on applications and extensions of VBLAST [7,8]. For example, Sfar et al. extended the SM-based MIMO systems to SM-based MIMO CDMA systems and presented a layered space-time (LAST) MUD that detects transmitted messages symbol by sym- bol [7]. The symbol-based LAST MUD is actually a variant of VBLAST; however, its computational com- plexity is very high, so it is not feasible in practice. To reduce the compu tation al co mp lex ity, a user-b ased LAST MUD was proposed in [8]. The mechanism is similar to the symbol-based LAST MUD, but it performs layered symbol detection user by user. In contrast to the sym- bol-based LAST MUD, the user-based LAST MUD re- duces the computational complexity at the expense of performance degradation. Furthermore, like VBLAST, both of the LAST MUD schemes need to rank the detec- tion order of the residual layered signals before detecting the symbols in each layer. Hence, they inevitably incur an extra computational overhead and also suffer from serious latency problems. Furthermore, the results re- ported in [7,8] demonstrate that the performance of MUDs degrades substantially when the length of the signature codes decreases. To resolve the above prob- lems, it is necessary to develop advanced layered detec- tion schemes for such CDMA-like systems. In this paper, our objective is to exploit the ad vantages of FT-domain spread MC DS-CDMA and MIMO sys- C opyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI 120 tems in order to provide advanced QoS in future wireless communications. To this end, we investigate the uplink of a multiuser MIMO FT-domain spread MC DS-CDMA system, which is an extension of th e MIMO CDMA sys- tem considered in [7,8]. In the proposed FT-domain spread MC DS-CDMA system, users are also arranged in groups; and each user is assigned a unique T-domain signature code and shares an F-domain signature code with users in the same group. Furthermore, like the SM method, each user employs his/her T-domain and F-domain signature codes to spread the multiple symbols. The spreading signals are then transmitted in parallel from the corresponding multiple antennas over fading channels to the antenna array at the base station. How- ever, the MAI effect, which is caused by the non-orthogonality of signature codes and is the main performance limitation, also affects the investigated MC DS-CDMA system. To mitigate the MAI effect, we pro- pose a one-user soft-decision aided user-based layered (OUSDA-UL) MUD. Our approach ranks the detection order by exploiting users' effective code correlation ma- trices, and then performs layered symbol detection with the assistance of the previous user's soft decisions [9]. That is the proposed OUSDA-UL scheme sequentially detects a subset of all transmitted symbols stage by stage (i.e. user by user). Moreover, in each stage, the soft deci- sions for the corresponding transmitted symbols are es- timated in parallel and collected for use in the next stage's symbol detection operation. To further reduce the computational complexity, we propose a one-group soft-decision aided group- based layered (OGSDA-GL) MUD. It estimates more transmitted symbols in parallel than the proposed OUSDA-UL scheme; hence, its com- putational complexity is lower. To enable a trade-off between the system performance and computational complexity, the two schemes only utilize one user's (or one group's) soft decisions to facilitate user-based/group-based layered detection. The soft mechanisms incorporated by existing works usually en- hance the system performance at the expense of high computational complexity. Under the trade-off between the performance and computational complexity, the pro- posed schemes only return partial soft decisions (i.e. one-user's soft-decisions or one-group's soft-decisions) to mitigate interference in the nex t stage. Finally, the results of extensive simulations show that the proposed MUDs outperform existing approaches and their computational complexity is modest. Before discussing the system model, we introduce the notations used throughout the paper: , {}E()T , () , and denote the expectation, the transpose, the Hermitian, and the fast Fourier transform (FFT) opera- tions respectively [10]; denotes the Kronecker prod- uct operator [10]; and ()FFT || |||| || represent the Euclidean norm and the Frobenius norm respectively [10]; and I, 0, and 0 denote the M identity matrix, the 1P zero vector, and the zero matrix respectively. The ranges of the indices and LL ,, ,ilk are 1 iM , 1T lM , 1kK , and 1 G respectively. We ex- plain , T , , and in Section II. KG 2. Signal Model Consider a synchronous uplink multiuser MIMO FT- domain spread MC DS-CDMA system. Each user is as- signed a unique T-domain signature code and T transmit antennas, which are deployed under the SM- based symbol transmission method. In addition, as in [7, 8], users are organized into G groups, and users in the same group share a unique F-domain signature code. For ease of presentation, we assume that the number of users in each group is K. Denote kkk kt andf, respectively, as the T-domain and F-domain signature codes of the kth user in the gth group. Here, and ,1 , tt 2 ] gt,T gN =[ gg t ,1 , ff 2 ] g t N , g f f=[ gg T N N are the processing gains of the corresponding signature codes. Each user employs his unique T-domain signature code to spread the T binary phase shift keying (BPSK) modulated symbols. Then, the T-domain spreading signals are copied to N sub-carriers, and spread by using the corresponding F-domain signature code. After spreading the symbols in the T-domain and F-domain, applying the inverse FFT algorithm, and inserting a cyclic prefix (CP) [2], the user's T spreading signals are transmitted in parallel by the T transmit antennas over the complex-valued, frequency selective Rayleigh fading channels to the base station. Let receive antennas be deployed at the base station. For simplicity, we assume that the length of all fading channels available to all users is equal to [11]. In addition, the complex-valued channel coeffi- cients between the ith receive antenna and the lth trans- mit antenna of the kth user in the gth group are denoted as ,,gl gl kk . We also assume that after re- moving the CP and performing the FFT operation, the signal will be received successfully. As a result, at the base station's receiver, the corresponding Q {(h1), i ( i )}Qh f NN di- agonal matrix of the F-domain channel's transfer function is ,, (1), l 1 , i N k = gl ([), T f hh QH0( gl ]) Q ii N g kk f diag FFT; Hence, the associative effective F-domain signa- ture code is , ,= ii gl gl k k. Now, the signal received at the base station's ith receive antenna can be expressed as follows: fHf , =1 = M Ti gl k l rc , =1 gl k gk =1 b ii ,n GK (1) where ,, ii = gl gl kk k cft is the effective 1 ft NN FT- Copyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI 121 domain signature code between the base station's ith re- ceive antenna and the lth transmit antenna of the kth user in the gth group; and is the corresponding i n1 ft NN additive white Gaussian noise (AWGN) vector with each entry )(0, 2 . For ease of expression, we stack the T transmitted BPSK symbols of the kth user in the gth group to form the user-based transmitted symbol vector and then re-express (1) as follows: ,1 ,2 =[ gg g kk bb ,1 =[ ii gkgk gk Cc , , ]T gM kT b =1 = GK i i g gk k rC ] i c , , k =1gk ,2 i c b . (2) i nb Here, ,gk MT is the corresponding t MT NN user-based effective FT-domain spreading matrix between the ith receive antenna and the kth user in the gth group. Similarly, we can stack the K transmitted symbol vectors k b of the gth group as a 1 T KM group-based transmitted symbol vector 12 ,, TT gg b = ii gg =[ g,bb =1 G g ] T T g K b. Then, (2) can be re-written as follows: , i rCb ] i n (3) where 12 g =[ ii ggg i CCCC is the effective associative t K TT b T M ] T T G b 1 T GKM NN =[ group-based FT-domain spreading matrix between the ith receive antenna and the gth group. Then, by stacking the G group-based symbol vectors, , we can re-express (3) as follows: where 12 and 12G are the corre- sponding transmitted symbol vector and the effective 1,G bb , i n= ii rCb ] i Cbb =[ ii CCC i t NN GKT M FT-domain spreading matrix between the ith receive antenna and all the transmit an- tennas. Finally, following [7,8], we use the effective FT-domain spreading matrices, to match the corresponding signals received by the base station's , i C receive antennas. Then, the sufficient statistics for the received signal at the base station can be formulated as follows: =1 = RH ii zCr=R bu, M i C (4) where i is the effective spatial-frequency- =1 =MRH i i RC time (SFT) code correlation matrix; and u is the corre- sponding complex Gaussian noise vector with )(0, 2R . 3. The Proposed One-User-Soft-Decision Aided User-Based Layered MUD The proposed OUSDA -UL MUD fir st ranks the detection order based on the users’ effective code correlation ma- trices. Then, it utilizes the ordered results to successively implement the corresponding user-based MMSE layered detectors and estimate the transmitted symbols. 3.1. User-based Ordering To avoid a large computational overhead for ranking the detection order, the proposed OUSDA-UL MUD com- putes the Frobenius norm [10] of the users' effective SFT code correlation matrices and then sorts the matrices in a descending order. For the kth user in the gth group, the Frobenius norm is formulated as follows: =1 ||||=||||, MRH ii F gg kkk i RCC F (5) where k R is the effective SFT code correlation matrix of the kth user in the gth group. Note that we assume the coefficients of the user’s fading channels are fixed in a frame and change frame by frame [5]. Hence, for each user, (5) is computed in just one pass per frame. As a result, the proposed scheme avoids the ordering problem observed in [6-8], which affects VBLAST-like schemes. In [6-8], the ordering mechanisms compute undetected symbols stage by stage (i.e. symbol by symbol, or user by user) by searching the maximization post signal-to- noise-ratio outputs of the corresponding detectors. How- ever, because the detectors for the undetected symbols need to be computed stage by stage, the computational complexity is usually prohibitive. 3.2. User-based Interference Cancellation and Layered Symbol Detection Without loss of generality, we assume that (1) after the user-based ordering step, the indices of the detection or- der are 12 1, 1, , , , kK G 12 1, 1, , k ; and (2) the interference caused by users 2 has been estimated pre- cisely and removed from the received signal. Then, in this step, we perform user-based layered symbol detec- tion and interference cancellation (IC) to estimate the transmitted symbols for the kth user in group g. Using , the residual sufficient statistics of the corresponding signal () 1 gk z can be formulated as 11 1 = gg gg kk kk zRbu 1 , (6) where 1 gk R is the sub-block matrix obtained by re- moving the corresponding rows and columns of the th, th, , 1 1 2 12k th users from the effective SFT code correlation matrix R; and 1 is the corresponding Gaussian noise vector. Then, to estimate the transmitted symbols of the gk u k th user k b, we utilize the user-based layered MMSE symbol detector with the soft decisions of the 1k th user and derive 2 11 ,1 ||||, min Hg gg gk kk k gg kk arg E Wb bWz b (7) where k W denotes the k th user's layered T DM Copyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI 122 MMSE symbol detector in which =() T DGgKM (2) T kM ; 1 gk b is the soft information vector gleaned from the 1 T M 1k th user’s soft decisions. From (7), it is clear that the proposed OUSDA-UL MUD attempts to fully exploit the last user’s soft information vector 1 gk b in order to enhance the performance of the kth user in the gth group. Using (7), and after some ma- nipulation, k W and 1k g b can be formulated as fol- lows: 1 })({EE 111 1 {{ }), HH gg g gg kk k kk E z zb 1 } T g k gk zb=(Wz (8) and 1 1={ Hg gg k kk E bWz }, (9) respectively. Furthermore, we assume that the transmit- ted symbols and noise are mutually uncorrelated and the transmitted symbols are BPSK modulated and i.i.d. [11]. We also assume that the transmitted symbols are BPSK modulated because of the ease of derivation. In addition, we assume that the transmission signals of the 1 1th, 2th, , 1k2 th users have been estimated exactly and removed from z in (4). Hence, the residual sufficient sta- tistics 1 gk z in (6) contain the transmission signals of the 1k th, k th, , and Gth users. Note that, be- cause we utilize the 1k th user's soft decisions when estimating the k th user's transmitted symbols k b in (7), 1 gk z must contain the 1k th user's transmitted signal. Based on the above assumptions and after some manipulations of (9) and (10), we have 11 1 {}= {} gg g kk k EE zRb, (10) () 1 {}= gk T g k gk E zb R 1 , g k (11) 2 11 111 11 {}={} HTH gg ggg gg kk kkk kk EE zzRbb RR, (12) where ,1 ,2, 111 1 ˆˆˆ {}=[, , , ,] TT ggg gM kDM kkkTT Ebbb b0. Here, ,, 11 1 ˆ=tanh( ()), 2 gl gl kk bb and , 1 () l k b is the soft decision [9] for the BPSK symbol of the th user in the gth group transmitted by the lth transmit antenna; (1)k() 1 gk gk R is the sub-block ma- trix of the SFT code correlation matrix T DM 1 gk R for the kth user of the gth gr o up; a n d 11 11 {} {}= T gM g kT k T gg MM kk TT MT E E bb 00 bb0 II , M T (13) where ,, 11 , 11 ˆˆ,, [{}] =1, , gigj kk T gij g kk bb ij Eotherwise bb (14) where denotes the (, th entry of matrix . After some manipulations (described in the Appendix) we have , [] ij X)ij X () 111 1 =() , gk Hg gDD k k WIABBAR (15) where we let 2 11 11 ={ } TH gg gg kk kk E 1 g k ARbbRR and 11 ={ gg kk E } BRb . Using (15) to find 1 gk b, (9) can be rewritten as follows: 1 1 ={ g g k k E bYR b 1 }. g k (16) where () 111 1 =(()) gk H g DD k YIABBAR. We also de- rive the expression of the above soft decision , 1 () l k b in (10). For this, we denote the th column of l k W as :, [] gl k W, which is the layered MMSE symbol detector for the kth user in the gth group transmitted from the lth transmit antenna. In addition, we let , 1 l k b (1)k, be the cor- responding soft information of the th user in the gth group, which is the lth entry of 1 gk b in (16). Then, we can express the corresponding output of the layered MMSE symbol detector as follows: ,:, 11 =[], Hg g, llg k k kk yb Wz l (17) Furthermore, following [9], we regard the output of the layered MMSE detector, , 1 l k y, as approximately Gaussian. Hence, the corresponding soft decision can be represented as ,,, , ,2 ,, , (|=1)2 ()=log= , (|=1) lglglgl kkk k gl kgl glgi kk k py bym bpyb (18) where , i k m and 2, i k are the corresponding equiva- lent mean and variance of the layered MMSE detector's output, expressed as () ,,, :, :, 1 22:, :,:, 1 1 , ={}=[ ][], ={[] }=[][] gk Hg g gl glgll lk k kkk HH g gg gg l ll k kk kk gl k mEyb var WR Wu WRW, where () :, 1 [] gk gl k R is the lth column vector of () 1 gk gk R. Note that, for the kth user in the gth group, we use (15) and (16) to apply the T layered MMSE symbol detectors :, [],=1 ,M T glT klW concurrently. Then, we utilize the corresponding soft decisions in (18) to help detect the T symbols of the th user in the gth group. In other words, the proposed OUSDA-UL MUD esti- mates the (1)k T transmitted symbols user-layer by user- layer. 4. The Proposed One-Group-Soft-Decision Aided Group-Based Layered MUD To reduce the computational complexity of estimating transmitted signals, we propose the OGSDA-GL MUD scheme. It is similar to the OUSDA-UL MUD scheme, but it detects transmitted symbols in a group-layer by group-layer manner. The steps of OGSDA-GL MUD are Copyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI 123 detailed below. 4.1. Group-based Ordering Similar to the OUSDA-UL MUD, the signals of the group-layers are or d ered by usin g th e Froben iu s nor ms of the groups’ effective SFT code correlation matrices, given by =1 ||||=|||| , MRH ii Fgg i RCC F (19) where R is the gth group's effective SFT code corre- lation matrix. Here, i C is the corresponding effective FT-domain signature matrix defined in (3). 4.2. Group-based IC and Layered Symbol Detection Without loss of generality, we assume that after the group-based ordering step, the order of the indices is 1, 2, , G. We also assume that the interference caused by the transmitted signals of the 1st, 2nd, , (2)g th groups was estimated precisely and removed from the received signal in (4). Then, as in (6), the sufficient sta- tistics of the corresponding residual signal, 1 z, can be expressed as follows: 111 = gggg zRbu 1 , (20) where 1 R (2)g is the sub-block matrix derived by remov- ing the corresponding rows and columns of the 1st, 2nd, , th groups from the SFT code correlation ma- trix R; and and 11 =[, , , ] TT TT gg gG bbb b 1 u are the associative residual symbol vector and noise vector re- spectively. Furthermore, similar to (7)-(16) and based on the MMSE method, the group-based layered MMSE de- tector W 1 and the corresponding soft information vec- tor b of the th group can be expressed as (1)g () 111 1 =() , H gg DD WIABB AR (21) and () 111 111 1 =(()){ }, g HH ggg g DD E bIABBARRb (22) respectively, where we let 2 1111 ={ } H T1 gg g g E ARb bRR } and . 11 ={ gg E BRb In addition, ; =(2) T DGg KM 1( 1),1( 1),2( 1), 11 {}=[{}, {}, , {},] TT gg ggM KT DKM T EEbEbEb b 0 , ,j and 11 11 {} {}= T gKMKM gTT T gKMKM gTT KMT E E bb 00 bb 0 II (23) where (1)(1) ,, 12 1, 1 ˆˆ, [{}]=1. gg kikj T gmn g bb klori Eotherwise bb (24) Here, we let 1 =(1) T mk Mi and 2 =(1) T nkM j =1 T M () , where , and . Finally, we assume that the outputs of the group-based layered MMSE detectors in (21) and (22) are approximately Gaussian [9]. Then, the soft decision, , 12 kandk=1Ki and j l k b , for the kth user in the gth group transmitted by the lth transmit antenna can be expressed as follows: ,,, , ,2 ,, , (|=1)2 ()=log= , (|=1) lglglgl kkk k gl kgl glgl kk k py bym bpy b (25) where , l k y , , l k m , 2, l k denote the corresponding group-based layered MMSE detectors' output, the mean of the output, and the noise power of the output. They can be written as 11 ,:, =[][], Hgg lgp p k y Wz b (26) () ,:,: 1 =[] [], g H, lgp g k m WR p (27) 22:,1:, ,=[ ][], H pg gp gl k WRW (28) respectively, where =(1) T pk Ml . Note that, based on (20)-(27), the proposed OGSDA-GL MUD estimates the T M transmitted symbols of the gth group in parallel. It also exploits the soft decisions of the gth group to help the layered MMSE detectors estimate the transmitted symbols of the (g1) th group. This strategy enables the OGSDA-GL MUD to estimate the transmitted symbols group by group. 5. Simulation Results and Discussion We conducted computer simulations and a complexity analysis to assess the performance of the proposed schemes. For ease of presentation, we assume the chan- nels are complex-valued, frequency selective Rayleigh fading channels, the channel length Q is 3, and the num- ber of receive antennas, , is 4. In addition, the user concurrently transmits the spreading signals in parallel from the T transmit antennas over the fading chan- nels to the base station. In the simulations and complex- ity analysis, we compared the performance of the fol- lowing six schemes: the linear MMSE SIC [13], the decorrelating detector (DD) [4 ], the symbol-based LAST MUD [7], the user-based LAST MUD [8], the proposed OUSDA-UL MUD, and the proposed OGSDA-GL MUD. We use a single user's performance (i.e. the performance when the system settings are , =1G=1 , , and ) as the benchmark. Figures 1-4 show the bit er- ror rate (BER) versus the signal to noise ratio (SNR) re- sult of the compared schemes. =1 T M =4 R M To assess the proposed schemes, we assume the sys- Copyright © 2013 SciRes. CN 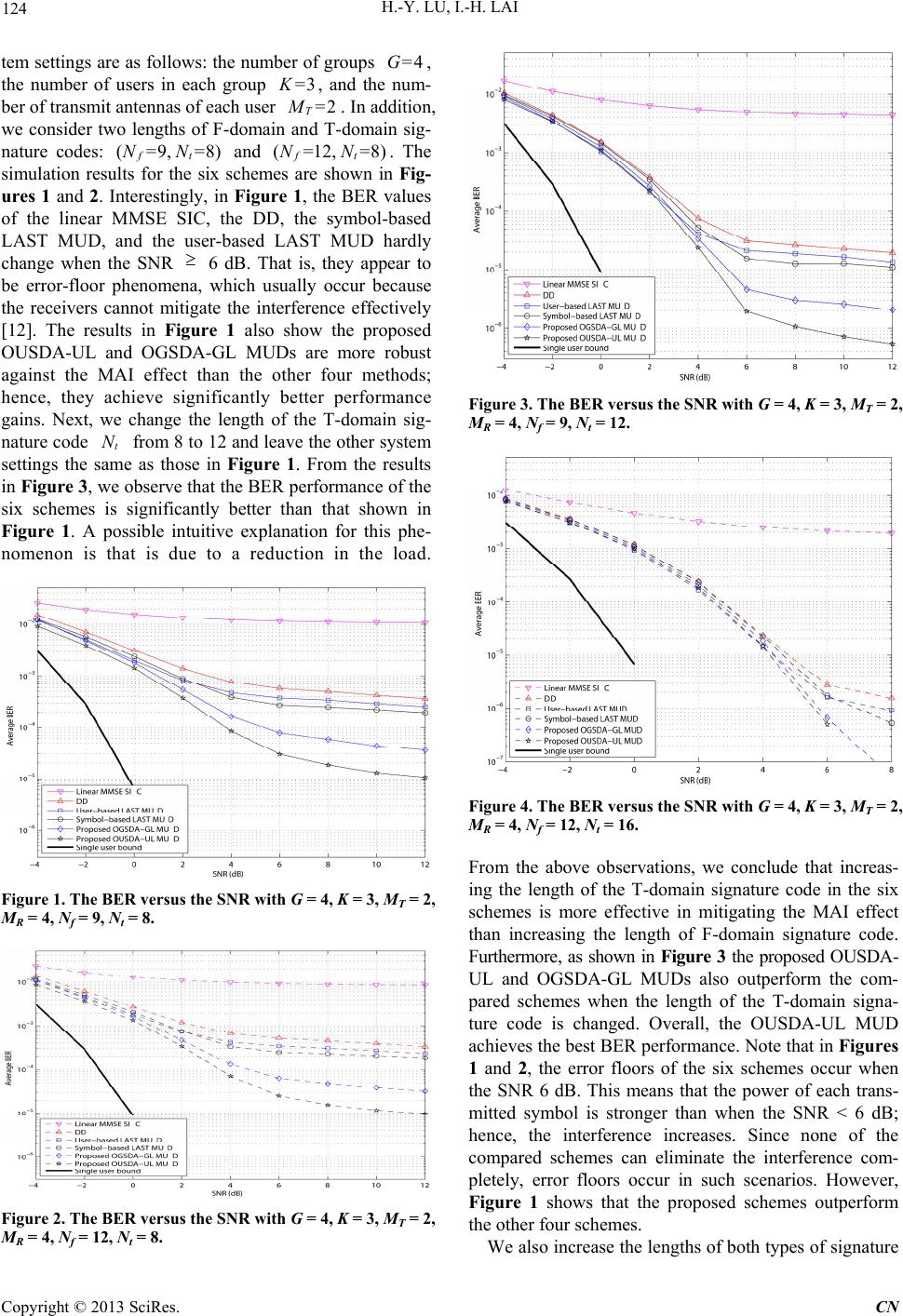 H.-Y. LU, I.-H. LAI 124 tem settings are as follows: the number of groups , the number of users in each group , and the num- ber of transmit antennas of each user . In addition, we consider two lengths of F-domain and T-domain sig- nature codes: and (= . The simulation results for the six schemes are shown in Fig- ures 1 and 2. Interestingly, in Figure 1, the BER values of the linear MMSE SIC, the DD, the symbol-based LAST MUD, and the user-based LAST MUD hardly change when the SNR 6 dB. That is, they appear to be error-floor phenomena, which usually occur because the receivers cannot mitigate the interference effectively [12]. The results in Figure 1 also show the proposed OUSDA-UL and OGSDA-GL MUDs are more robust against the MAI effect than the other four methods; hence, they achieve significantly better performance gains. Next, we change the length of the T-domain sig- nature code from 8 to 12 and leave the other system settings the same as those in Figure 1. From the results in Figure 3, we observe that the BER performance of the six schemes is significantly better than that shown in Figure 1. A possible intuitive explanation for this phe- nomenon is that is due to a reduction in the load. =4G 8) t =3K T M N =2 12, f (=9, =8 ft NN t N ) =N Figure 1. The BER versus the SNR with G = 4, K = 3, MT = 2, MR = 4, Nf = 9, Nt = 8. Figure 2. The BER versus the SNR with G = 4, K = 3, MT = 2, MR = 4, Nf = 12, Nt = 8. Figure 3. The BER versus the SNR with G = 4, K = 3, MT = 2, MR = 4, Nf = 9, Nt = 12. Figure 4. The BER versus the SNR with G = 4, K = 3, MT = 2, MR = 4, Nf = 12, Nt = 16. From the above observations, we conclude that increas- ing the length of the T-domain signature code in the six schemes is more effective in mitigating the MAI effect than increasing the length of F-domain signature code. Furthermore, as shown in Figure 3 the proposed OUSDA- UL and OGSDA-GL MUDs also outperform the com- pared schemes when the length of the T-domain signa- ture code is changed. Overall, the OUSDA-UL MUD achieves the best BER performance. Note that in Figures 1 and 2, the error floors of the six schemes occur when the SNR 6 dB. This means that the power of each trans- mitted symbol is stronger than when the SNR < 6 dB; hence, the interference increases. Since none of the compared schemes can eliminate the interference com- pletely, error floors occur in such scenarios. However, Figure 1 shows that the proposed schemes outperform the other four schemes. We also increase the lengths of both types of signature Copyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI 125 codes from to , while maintaining the system settings shown in Figure 1. From the results presented in Figure 4, we observe that all six schemes perform better than in the scenarios discussed above (i.e., Figures 1, 2, and 3). This is reasonable be- cause increasing the lengths of the F-domain and the T-domain signature codes individually can mitigate in- ter-group MAI and inter-user MAI respectively. In this scenario, the proposed OUSDA-UL MUD and OGSDA- GL MUD achieve the best and second best performance gains among the six compared schemes. (=9, =8 ft NN)(=12, =16) ft NN Next, we analyze the computational complexity of the six compared schemes. Because computing the inversion of a matrix generally dominates the computational com- plexity, we focus on that aspect of the schemes. For the propos ed OUSDA-UL MUD and OG SDA-GL MUD, we compute the corresponding complex multiplications and additions (CMAs) needed for Equations (15) and (21). Furthermore, approximately complex CMAs are needed to find the inversion of a matrix. For ease of reference, we show the expressions of the computa- tional complexity for the six schemes in Table 1. For example, in the scenario, the lin- ear MMSE SIC, the decorrelating detector (DD), the symbol-based LAST MUD, the user-based LAST MUD, the proposed OUSDA-UL MUD, and the proposed OGSDA-GL MUD r equire 13844, 13824 , 90000, 48672, 97344, and 43200 CMAs respectively. Therefore, the proposed OUSDA- UL MUD needs the largest number of CMAs among the six schemes. This is because it ex- ploits the last user’s soft decisions to help improve the BER performance, but the price is an increase in the computational overhead. Meanwhile, the proposed OGSDA-GL MUD needs fewer CMAs than the sym- bol-based LAST MUD, but more than the user-based LAST MUD. The linear MMSE SIC scheme requires the second lowest amount of computation, but its BER per- formance is the worst among the six schemes. 3 P , T M PP =2)(=4 ,=3GK Table 1. Comparison of the computational complexity of the proposed schemes. MUDs Complex multiplications/additions Linear MMSE SIC TT GKMGKM 3 )( DD 3 )( T GKM Symbol-based LAST 3 1 0= )(iGKMT T GKM i User-based LAST 3 1 0= )*( TT GK iMiGKM Proposed OUSDA-UL 3 1=1=3D K k G g Proposed OGSDA-GL 3 1= 3D G g 7. Conclusions We have investigated layered symbol detection strategies for the uplink of a multiuser MIMO frequency-time- domain spread MC DS-CDMA system. First, we pro- posed a scheme called OUSDA-UL MUD, which ex- ploits the last user's soft decisions to help mitigate the MAI effect and improve the BER performance. Second, to reduce the computation al complexity, we proposed the OGSDA-GL MUD, which exploits the last group’s soft decisions to facilitate layered symbol detection. The re- sults of simulations and a complexity analysis demon- strate that the proposed schemes yield better BER per- formance gains than existing approaches, but their com- putational overheads are modest. 8. Acknowledgements This work was supported by National Taiwan Ocean University of R.O.C. under contract NTOU-101-002. REFERENCES [1] M. Jiang and L. Hanzo, “Multiuser MIMO-OFDM for Next-generation Wireless Systems,” Proceedings of IEEE, Vol. 95, No. 7, 2007, pp. 1430-1469. doi:10.1109/JPROC.2007.898869 [2] M. Guenach and H. Steendam, “Performance Evaluation and Parameter Optimization of MC-CDMA,” IEEE Trans. Vehicular Technology, Vol. 56, No. 3, 2007, pp. 1165-1175. doi:10.1109/TVT.2007.895605 [3] C. W. You and D. S. Hong, “Multicarrier CDMA Sys- tems Using Time-domain and Frequency-domain Spread- ing Codes,” IEEE Trans. Commun., Vol. 51, No. 1, 2003, pp. 17-21. doi:10.1109/TCOMM.2002.807630 [4] B. Hu, L.-L Yang and L. Hanzo, “Time- and Frquency- Domain-spread Generalized Multicarrier DS-CDMA Us- ing Subspace-based Blind and Group-blind Space-time Multiuser Detection,” IEEE Trans. Vehicular Technology, Vol. 57, No. 5, 2008, pp. 3235-3241. doi:10.1109/TVT.2008.917231 [5] A. Paulraj, R. Nabar and D. Gore, Introduction to Space-Time Wireless Communications, Cambridge Uni- versity Press, 2003. [6] G. J. Foschini, G. D. Golden, R. A. Valenzuela and P. W. Wolniansky, “Simplified Processing for High Spectral Efficiency Wireless Communication Employing Multi-element Arrays,” IEEE J. Select. Areas Commun., Vol. 17, No. 11, 1999, pp. 1841-1852. doi:10.1109/49.806815 [7] S. Sfar, R. D. Murch and K. B. Letaief, “Layered Space-time Multiuser Detection over Wireless Uplink Systems,” IEEE Transactions Wireless Communications, Vol. 2, No. 4, 2003, pp. 653-668. doi:10.1109/TWC.2003.814337 [8] S. Sfar and K. B. Letaief, “Layered Group Detection for Multiuser MIMO Wireless CDMA Systems,” IEEE Transactions Wireless Communications, Vol. 5, No. 9, Copyright © 2013 SciRes. CN  H.-Y. LU, I.-H. LAI Copyright © 2013 SciRes. CN 126 2006, pp. 2305-2311. doi:10.1109/TWC.2006.1687748 [9] X. Wang and H. V. Poor, Wireless Communication Sys- tems. Pearson Edu., Inc., NJ, 2004. [10] T. K. Moon and W. C. Stirling, Mathematical Method and Algorithms for Signal Processing. Prentice Hall, 2000. [11] J. G. Proakis and M. Salehi, Digital Communications. 5th ed. McGraw-Hill, 2008. [12] R. C. de Lamare and R. Sampaio-Neto, “Minimum Mean- squared Error Iterative Successive Parallel Arbitrated De- cision Feedback Detectors for DS-CDMA Systems,” IEEE Transactions Communications, Vol. 56, No. 5, 2008, pp. 778-789. doi:10.1109/TCOMM.2008.060209 [13] A. Bentrcia, A. Zerguine, A. U. Sheikh and M. Benyoucef, “A New Linear Group-wise SIC Multiuser Detector,” IEEE Communications Letters, Vol. 11, No. 2, 2007, pp. 176–178. doi:10.1109/LCOMM.2007.061472
|