Communications and Network, 2013, 5, 113-118
http://dx.doi.org/10.4236/cn.2013.53B2022 Published Online September 2013 (http://www.scirp.org/journal/cn)
User Fairness Scheme with Propo r ti o nal Fair Sch e d u li n g
in Multi-user MIMO Limited Feedback System
Hongyu Wang, Weixiao Meng, Trungtan Nguyen
School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin, China
Received June, 2013
ABSTRACT
In Multi-user MIMO (MU-MIMO) downlink system, suitable user selection schemes can improve spatial diversity gain.
In most of previous studies, it is always assumed that the base station (BS) knows full channel state information (CSI)
of each user, which does not consider the reality. However, there are only limited feedback bits in real system. Besides,
user fairness is often ignored in most of current user selection schemes. To discuss the user fairness and limited feed-
back, in this paper, the user selection scheme with limited feedb ack bits is proposed. The BS utilizes codebook precod-
ing transmitting strategy with LTE codebook. Furthermore, this paper analyzes the influence of the number of feedback
bits and the number of users on user fairness and system sum capacity. Simulation results show that in order to achieve
better user fairness, we can use fewer bits for feedback CSI when the number of user is small, and more feedback bits
when the number of users is large.
Keywords: MU-MIMO; User Scheduling; User Fairness; PFS; Limited Feedback
1. Introduction
In Multi-user MIMO downlink system, the BS can inde-
pendently transmit data streams to different user utilizing
the same time-frequency resources. It is called space di-
vision multiple access (SDMA), which can bring more
throughput due to multi-user division gain. Multi-user
MIMO has been included in 3GPPLTE [1] and LTE-
Advance standard. In downlink transmit strategy, the
dirty paper coding (DPC) has been proved to achieve the
optimal capacity in [2]. But in real system, it is difficult
to realize due to its high complexity. So some subopti mal
schemes are studied, in which the Zero-forcing beam-
forming (ZFBF) is a classic scheme. It is shown in [3]
that in the condition of larg e number of users, the cap ac-
ity of ZFBF approaches to DPC.
Full CSI of all the users is required in both the DPC
and the ZFBF. Otherwise, the system throughput will
reduce severely [4]. However, full CSI requires larger
bandwidth to feedback which is unrealistic, since the
number of feedback bits is always limited in real-world
systems. Currently, most studies focus on improving the
sum rate with limited feedback bits [5,6].
In Multi-user MIMO systems, the system sum rate will
be severely affected by multi-user interference since the
BS transmits to multiple users simultaneously. Accord-
ingly, it is necessary to pick up the users with good spa-
tial orthogonality to transmit. Furthermore, since the
number of antenna in the BS is fixed, when the number
of user is larger than the number of antennas, user sched-
uling is needed. User selection can achieve spatial diver-
sity gain, and further increase sum rate in [7]. [8] shows
that semi-orthogonal user selection (SUS) can reduce
multi-user interference effectiv ely by schedulin g multip le
users that have small space correlation. However, SUS
assumes that the BS knows the CSI completely, which is
unavailable in limited feedback systems. Most of multi-
user scheduling schemes use the fixed beamforming
codebook. The user calculates the signal-to-interference-
plus-noise ratio (SINR) with each codeword and feed-
back the codeword index which achieves maximum
SINR along with the SINR value. Then the BS selects the
user with the highest SINR on every codeword and uses
the codebook as pre-coding matrix for downlink trans-
mitting. In most user scheduling algorithms, user fairness
is not considered, but in practice it is often important to
take care of the bad channel users. The PFS provides
fairness among user s. In [9,10], the user average capacity
is considered to avoid the bad channel users not being
served for a long time.
In this paper, we consider LTE codebook as the lim-
ited feedback codebook. In LTE codebook, the codeword
in the same sub-codebook are orthogonal, while the
codeword in different sub-codebook are not orthogonal.
So the BS must select the codeword in the same
sub-codebook as the beamforming weight vector. User
C
opyright © 2013 SciRes. CN

H. Y. WANG ET AL.
114
feedback the codeword index, which achieves the maxi-
mum SINR and the corresponding SINR value, the BS
schedules users with the max system sum capacity
among the sub-codebooks. Using LTE codebook and
PFS, we consider the user fairness with different number
of feedback bits on the condition of different number of
users.
2. System Model
In this paper, we consider multi-user MIMO downlink
system. Figure 1 shows the system channel model. The
BS configures N antennas and each user has single an-
tenna. The BS can communicate with K(
K
N
KM
1N
C
) users
simultaneously. The number of user is M(). De-
note the channel vector of user k by , where we
assume the entries of k are independent but
non-identically distributed complex Gaussian random
variables with zero mean. Different variance represents
different channel condition. The BS selects a
sub-codebook as beamforming matrix
kh
h
()
N
N
C Wand
form N orthogonal beams. Each beam is the column
vector of . Then the BS communicates to the selected
K users simultaneously in one time slot. The receive sig-
nal of user k can be expressed as
w
W
1,
N
kkkii
ik
y
Psn


hw 
(1)
where the is the normalized transmitted sym-
bol from the BS which satisfies , k is addi-
tive white Gaussian noise (AWGN) vector, and k is
transmit power of the kth user. The BS has an average
power constraint, which is 1k. In this paper,
the channel is time varying Rayleigh fading channel.
Assume the user knows its own channel k perfectly.
LTE codebook set is , where
1N
C s
()
*
{}1Ess
N
k
PP

( 1)
, }
G
E
()
[]
nP


h
(0)
{,E
()
01
g
gg
C eNN
N

() 1gN
Ee
is the sub-codebook, and m is the codeword.
Then the kth user computed the SINR over the mth code-
word in the gth sub-codebook as:
Ce
1
2
N
…
BS
User 1
…
User K
User 2
User K+1
…
User M
…
User Terminal
User Selection
Precodi ng
Power Allocation
Feedback
Channel
Figure 1. System Channel Model.


2
,, 2
1,
,
1
g
km
kgm Ng
ki
iim
SINR



he
he (2)
where 1, 2,,kK

, 1, 2,,
g
G

, . G
is the number of sub-codebook, which decides by the
number of feedback bit. Then the terminal user feeds
back the maximum SINRk,g,m and the corresponding co-
deword index (g, m). The BS selects the maximum SINR
user for each codeword. For each sub-codebook g, the
BS computes the sum rate Rg as:
1, 2,,mN
,,
1log(1 argmax)
N
g
kgm
k
m
P
RS
N


INR
(3)
where P is the total transmitting power. In this paper, we
just consider equ al power allocation. Rg is the capacity of
the gth sub-codebook. For 1,2,,
g
G, the BS selects
the maximum Rg and the index g*.
*argmax
g
g
g
R

(4)
During the downlink transmission, the BS uses the
*
()
g
E
as the beamforming matrix. So we can get
*
()
g
WE .
3. PFS Scheme
Designed to maximize the sum rate, user scheduling
schemes often ignore user fairness, thus making the user
with the bad channel seldom served. Therefore, the qual-
ity of service (QoS) of these users will not be guaranteed
in a QoS sensitive system. The PFS scheme proposed by
Jalali and Padovani can solve this problem effectively.
The PFS considers the user’s current average throughput
in a period of time. Using the radio of instantaneous
channel quality and average throughput determines
whether the user can be scheduled, so it can take account
for the tradeoff between throughput and fairness. The
criterion of user selection is showed as:
 
*
1,2, ,
1
arg max,
k
kK
k
kR
t 

t (5)
where is the instantaneous rate of the kth user, ()
k
Rt
()
kt

is the average throughput of the kth user in past tc
time slot which is update by formula (6) every time slot.

 

*
*
11
1
11
1
kk
cc
k
k
c
tRtkk
tt
t
tk
t




k



 








(6)
The traditional PFS before only select one user in each
time slot. But in this paper, the BS needs to communicate
with more than one user at the same time, so we modify
the traditional PFS to adapt to the multi-user MIMO

H. Y. WANG ET AL. 115
case.
In our system, the BS transmits to more than one user
simultaneously. But for each codeword, only one user
can be selected. So in the tth time slot, the BS schedules
user for the mth codeword in the gth sub-codebook using
the traditional PFS scheme which can be described as:
 
*
,
1,2, ,
1
arg max
gm kgm
kK
k
kR
t 


,
,
t (7)
where ,, is the instantaneous date rate of the kth
user on the (g, m) codeword, and
()
kgm
Rt ()
kt

is the average
data rate of the kth user in the past tc time slots which is
updated as:

 

11
1
11
1
kk
cc
k
k
c
tRtk is scheduled
tt
t
totherwi
t






 





se
(8)
where is the instantaneous date rate of user k in
tth time slot.
()
k
Rt
4. User Scheduling Process
In this paper, we choose LTE codebook as local code-
book, [1] shows the generation methods of LTE code-
book. The number of sub-codebook is decided by the
number of feedback bit. And the antenna number in BS
determines the number of codeword in a sub-codebook.
The kth user achieves its channel state information
from the downlink pilot channel, and computes the SINR
value SINRk,g,m for each codeword (g, m). Then each user
feeds back the maximum SINR value SINRk,g*,m* and the
corresponding codeword index (g*, m*). The BS sched-
ules users at time slot using the following procedures:
th
t
Step 1: For each codeword (g, m), select the user k*
making ,,kgm maximum. Because the BS knows
the CSI by limited feedback, the equal power allocation
is suitable. So the maximum SINR means maximum the
data rate of each user.
SINR
*,,
argmax kgm
k
kSINR (9)
Step 2: For each sub-codebook g, compute sub-code-
book capacity:
 
*,,
1
,
N
gkgm
m
RtR t

 (10)
where .
*, ,
Step 3: Selecting 0*, ,
() log(1)
kgmkgm
Rt PSINR
*argmax()
1g gG
g
Rt
So the BS selects the sub-codebook g* as pre-coding
matrix, and the sum capacity of system is
.
*
g
() ()RtR t

It can be seen that the user selection scheme is based
on system sum capacity. If the PFS is considered, we can
get another user selection scheme. So we modify the Step
1 and add the Step 4.
Step 1: For each codeword (g, m), select the user k*
making


,,kgm k
SINR t  maximum.

,,
*argmax ,
kgm
kk
SINR
kt

 (11)
Step 4: Update the ()
kt

using formula (8).
In the following, the first scheme is called Non-PFS
scheme, and the second scheme is called PFS scheme.
The flow diagram of user selection with PFS can be
showed in Figure 2. In the flow diagram, i is
sub-codebook index, j is the codeword index in ith
sub-codebook. k is the user index. Here, we just show the
process of one time slot.
0i
0j
1ii
1jj

,,
*
argmax
kij
kk
SINR
kt


?jN
 *
,,
1
log 1
N
ikij
j
P
Rt SINR
N






?iG

*
1
argmax
i
iG
iRt






*
i
R
tRt


k
t 
Figure 2. User selection flow diagram.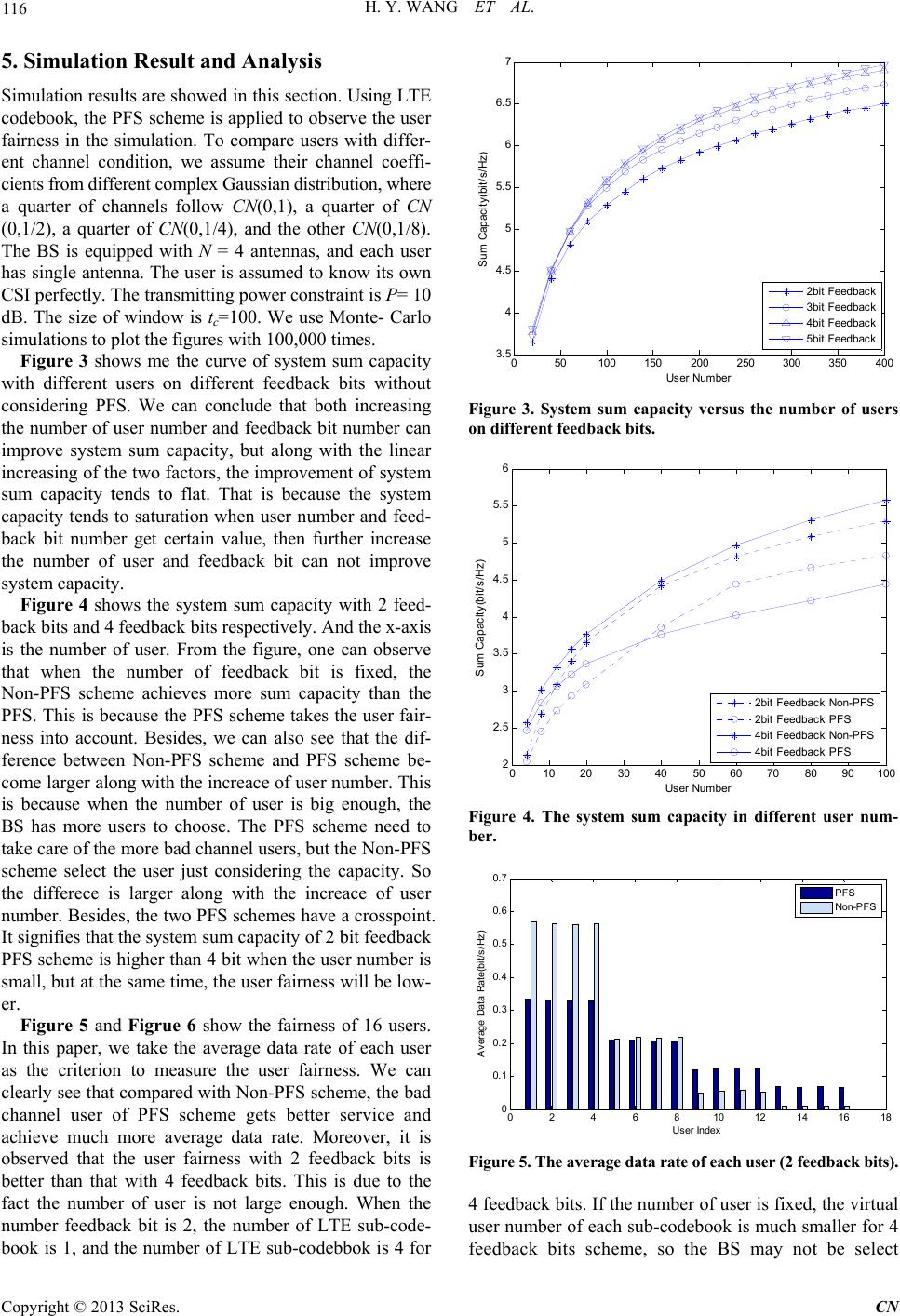

H. Y. WANG ET AL.
116
5. Simulation Result and Analysis
Simulation results are showed in this section. Using LTE
codebook, the PFS scheme is applied to observe the user
fairness in the simulation. To compare users with differ-
ent channel condition, we assume their channel coeffi-
cients from different complex Gaussian distribution, where
a quarter of channels follow CN(0,1), a quarter of CN
(0,1/2), a quarter of CN(0,1/4), and the other CN(0,1/8).
The BS is equipped with N = 4 antennas, and each user
has single antenna. The user is assumed to know its own
CSI perfectly. The transmitting power constraint is P= 10
dB. The size of window is tc=100. We use Monte- Carlo
simulations to plot the figures with 100,000 times.
Figure 3 shows me the curve of system sum capacity
with different users on different feedback bits without
considering PFS. We can conclude that both increasing
the number of user number and feedback bit number can
improve system sum capacity, but along with the linear
increasing of the two factors, the improvement of system
sum capacity tends to flat. That is because the system
capacity tends to saturation when user number and feed-
back bit number get certain value, then further increase
the number of user and feedback bit can not improve
system capacity.
Figure 4 shows the system sum capacity with 2 feed-
back bits and 4 feedback bits respectively. And the x-axis
is the number of user. From the figure, one can observe
that when the number of feedback bit is fixed, the
Non-PFS scheme achieves more sum capacity than the
PFS. This is because the PFS scheme takes the user fair-
ness into account. Besides, we can also see that the dif-
ference between Non-PFS scheme and PFS scheme be-
come larger along with the increace of user number. This
is because when the number of user is big enough, the
BS has more users to choose. The PFS scheme need to
take care of the more bad channel users, but the Non-PFS
scheme select the user just considering the capacity. So
the differece is larger along with the increace of user
number. Besides, the two PFS schemes have a crosspoint.
It signifies that the system sum capacity of 2 bit feedback
PFS scheme is higher than 4 bit when the user number is
small, but at the same time, the user fairness will be low-
er.
Figure 5 and Figrue 6 show the fairness of 16 users.
In this paper, we take the average data rate of each user
as the criterion to measure the user fairness. We can
clearly see that compared with Non-PFS scheme, the bad
channel user of PFS scheme gets better service and
achieve much more average data rate. Moreover, it is
observed that the user fairness with 2 feedback bits is
better than that with 4 feedback bits. This is due to the
fact the number of user is not large enough. When the
number feedback bit is 2, the number of LTE sub-code-
book is 1, and the number of LTE sub-codebbok is 4 for
050100 150200 250 300 350400
3. 5
4
4. 5
5
5. 5
6
6. 5
7
Us er Num be r
Sum Capacity(bit/s/Hz)
2bit F eedback
3bit F eedback
4bit F eedback
5bit F eedback
Figure 3. System sum capacity versus the number of users
on different feedback bits.
010 2030 40 50 60 7080 90 100
2
2.5
3
3.5
4
4.5
5
5.5
6
User Num ber
Sum Capacity(bit/s/Hz)
2bit F eedback Non-PF S
2bit F eedback PFS
4bit F eedback Non-PF S
4bit F eedback PFS
Figure 4. The system sum capacity in different user num-
ber.
024681012 14 1618
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
User Index
Average Data Rate(bit/s/Hz)
PFS
Non-PF S
Figure 5. The average data rate of each user (2 feedback bits).
4 feedback bits. If the number of user is fixed, the virtual
user number of each sub-codebook is much smaller for 4
feedback bits scheme, so the BS may not be select

H. Y. WANG ET AL. 117
0 2 4 6 810 12 14 1618
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
User Index
Average Data Rate(bit/s/Hz)
PFS
Non-PFS
Figure 6. The average data rate of each user (4 feedback bits)
010 203040 50 60 708090100
0
0. 05
0.1
0. 15
0.2
0. 25
Us er Numbe r
Average Data Rate(bit/s/Hz)
2bit F eedback Non-P F S
2bit F eedback PF S
4bit F eedback Non-P F S
4bit F eedback PF S
Figure 7. Bad channel user average data rate in different
user number.
enough users, it is helpful to good channel user. So it can
weaken the fairness. The simulation result of different
user number is demonstrated in Figure 7.
Next, we will analyze how the varying number of user
influences the user fairness. Here, we only consider the
bad channel users whose channel coefficient is from
CN(0,1/8) distribution. The simulation result of average
data rate of bad channel users with varying number of
users is shown in Figure 7. From the figure, we can
summary that, when the number of user is less than 35,
the bad channel user data rate of 2 bits feedback PFS
scheme is better than 4 bit feedback PFS scheme, when
the number of user is larger than 35, the bad channel user
data rate of 4 bits feedback PFS scheme is better than 2
bit feedback PFS scheme. It indicates that 2 bits feedback
PFS scheme leads to the better fairness when the number
of user is small and 4 bits feedback PFS scheme leads to
the better fairness when the number of user is large. So in
LTE system, when the number of user is small, we can
achieve better user fairness by choosing less feedback
bits; on the other hand, when the number of users is large,
we can obtain higher fairness by choosing more feedback
bits.
6. Conclusions
In this paper, we studied the performance of a general-
ized PFS scheme in limited feedback multi-user MIMO
downlink system, with the LTE codebook as local code-
book. It can be concluded that the PFS scheme can get
the tradeoff between sum capacity and user fairness. We
further analyzed the influence of the number of users and
the number of feedback bits on user fairness and capacity.
The simulation results show that, when the number of
users is small, we can use fewer bits to feedback user’s
CSI to achieve better user fairness, while more bits
should be used when the number of users is large.
7. Acknowledgements
This work is partly supported by the National Science
and Technology Major Project (2012ZX03004003) and
China National Science Foundation under Grand
No.61201148.
REFERENCES
[1] 3GPP, “Evolved Universal Terrestrial Radio Access
(E-UTRA); Physical channels and modulation,” 3GPP TS
36.211 version 10.0.0 Release 10.
[2] G. Caire and S. Shamai, “On the Achievable Throughput
of a MultiantennaGassian Broadcast Channel,” IEEE
Transactions on Information Theory, Vol. 49, 2003, pp.
1691-1706. doi:10.1109/TIT.2003.813523
[3] Q. H. Spencer, A. L. Swindlehurst and M. Haardt, “Ze-
ro-Forcing Methods for Downlink Spacial Multiplexing
in Multiuser MIMO Channels,” IEEE Transactions on
Signal Process, Vol. 52, No. 2, 2004, pp. 461-471.
doi:10.1109/TSP.2003.821107
[4] Masoud and B. Hassibi, “On the Capacity of MIMO
Broadcast Channels with Partial Side Information”, IEEE
Transanctions on Information Theory, Vol. 51, 2003, pp.
506-522.
[5] T. Yoo, N. Jindal and A. Goldsmith, “Multi-antenna
Downlink Channels with Feedback and User Selection,”
IEEE J. Select. Areas Commun., Vol. 25, No. 7, 2007, pp.
1478-1491. doi:10.1109/JSAC.2007.070920
[6] K. Huang, A. Texas Univ., R. W. Hearth and J. G. An-
drews, “Space Division Multiple Access with a Sum
Feedback Rate Constraint,” IEEE Transactions on Signal
Process, Vol. 55, No. 7, 2007, pp. 3879-3891.
doi:10.1109/TSP.2007.894245
[7] Y. X. Wang, S. Y. Hur, Y. W. Park and J.-H. Choi, “Effi-
cient User Selection Algorithms for Multiuser MIMO
Systems with Zero-forcing Dirty Paper Coding,” IEEE
Journal of Communications and Networks, Vol. 13, 2011,
pp. 232-239.
[8] T. Yoo and A. Goldsmith, “On the Optimality of Mul-
tiantenna Broadcast Scheduling Using Zero-forcing
Beamforming,” Ieee journal on Selected Areas in Com-
munications, Vol. 24, No. 3, 2006, pp. 528-541.
doi:10.1109/JSAC.2005.862421

H. Y. WANG ET AL.
118
[9] N. Sharma, “A Study of Opportunism for Multi-
ple-anrenna System,” IEEE Transactions on Information
Theory, Vol. 51, No. 5, 2006, pp. 1804-1814.
doi:10.1109/TIT.2005.846410
[10] Choi and Jeongsik, “User Thoughput Estimation for the
PF Scheduling Algorithm under MIMO Channel Envi-
ronments,” IEEE Wireless Communications Letters, Vol.
1, 2012, pp. 528-531.
doi:10.1109/WCL.2012.072012.120455