Communications and Network, 2013, 5, 108-112
http://dx.doi.org/10.4236/cn.2013.53B2021 Published Online September 2013 (http://www.scirp.org/journal/cn)
Pipeline structure Schnorr-Euchner Sphere Decoding
Algorithm
Xinyu Mao, Jianjun Wu, Haige Xiang
State Key Laboratory of Advanced Optical Communication Systems & Networks,
School of Electronics Engineering and Computer Science, Peking University, Beijing, China
Received May, 2013
ABSTRACT
We propose a pipeline structure for Schnorr-Euchner sphere decoding algorithm in this article. It divides the search tree
of the original algorithm into blocks and executes the search from block to block. When one block search of a signal is
over, the part in the pipeline structure that processes this block search can load another signal and search. Several sig-
nals can be processed at the same time in one pipeline. Blocks are arranged to lower the whole complexity in the way
that the previously search blocks are the blocks those have more probability to generate the final solution. Simulation
experiment results show the average process delay can drop to the range from 48.77% to 60.18% in a 4-by-4 antenna
system with 16QAM modulation, or from 30.31% to 61.59% in a 4-by-4 antenna system with 64QAM modulation.
Keywords: Multiple-Input Multiple-Output System; Schnorr-Euchner Sphere Decoding; Pipeline Structure
1. Introduction
With the rapid development of wireless communications,
the desire for high speed data service conflicts with the
situation that fewer and fewer band width is available.
Multiple-input multiple-output (MIMO), which can pro-
vide dramatic high spectral efficiency, is the key tech-
nology to resolve this conflict. MIMO is on e of the most
exciting technologies of the last decade [1,2].
The MIMO detection is rather a complex problem. The
maximum likelihood (ML) detection provides the opti-
mal performance. But its complexity is so high that it can
not be used in actual systems. The linear detection, such
as the zero forcing and minimum mean square error de-
tection have low computation complexity. But their per-
formance is very poor. The Vertical Bell Laboratories
Layered Space Time (VBLAST) detection provides
higher performance than the linear detection with the
price of small complexity increase [3]. But the perform-
ance is not good enough.
Sphere decoding (SD) algorithm was proposed to pro-
vide optimal performance or near optimal performance
with low complexity [4]. So it attracts much attention as
soon as it was propo sed [5]. Schnorr-Euchner SD (SESD)
algorithm is an optimized SD algorithm [6]. It can find
the optimal solution faster th an the original SD algorithm
and the modification from SD to SESD is very small. So
it is the most popular optimal performance algorithm
[7-15].
However, there are two main drawbacks which restrict
the usage of the SESD in actual systems, especially the
real time systems. One is that the calculation complexity
of the SESD is not fixed and changes in a large range.
Another is that it is not suitable to use in pipeline struc-
ture.
In this article, we propose a pipeline structure for
SESD algorithm. The searching process of SESD algo-
rithm is divided into blocks and can be executed sequen-
tially. When the multiple threads searching is executed
simultaneously, the processing time decreases. Simula-
tion experiment results show that the proposed structure
can save remarkable processing time especially in low
signal to n oise ratio ( SN R).
2. MIMO System and ML Detection
MIMO system can be depicted as an equation
y=Hs+n (1)
where s is the Nt×1 transmit vector. y is the Nr×1
receive vector, and n stands for the independent and
identical distributed complex zero-mean Gaussian noise.
H is the Nt×Nr channel matrix where hij is the complex
channel gain and satisfies 21
ij
Eh



. Usually when
Nr Nt, equation (1) can be calculated.
ML algorithm is to find the solution of
2
ˆargmin
ML 

s
sy-Hs (2)

X. Y. MAO ET AL.
109
where  means the set of all possible transmit vectors.
3. Tree Search and Euclidean Distance
For further disposition, the QR decomposition is always
used to make the channel matrix triangular. We know
that every matrix can be express as
H=QR (3)
equation (1) will be expressed as
ρ=Rs+η (4)
where H
ρ=Q y and H η=Q n. (4) can be rewritten as
11 121
22 2
111
222
0
00
00 0
00 0
Nt
Nt
NtNt
N
rNtNr
rr r
rr
s
s
r
s








 

 

 


 

 

 











(5)
The ML algorithm can be expressed as
2
ˆargmin

sρ-Rs (6)
where

12
ˆˆˆ ˆ
T
Nt
ss ss is the estimated value of
transmitted symbol. For sake of simplification, we set
N=Nt next.
From equation (5), it can be found that there is no in-
ference from other transmission signals on
N
s
. It can be
expressed as
N
NN NN
rs

  (7)
According to equation (7),
N
s
ca n be calc ul at ed by
ˆN
NNN
sround r




(8)
where ˆ
N
s
is the estimated transmit signal. When
N
s
is
known, 1N
s
 can be calculated by eliminated the inter-
ference of
N
s
. According to this idea, all transmit sig-
nals can be calculated by
1
1
ˆˆ
N
iiikk
ki
ii
sroundr s
r









 (9)
Equation (9) means the ith receive signal is determined
by the transmit signals from the ith to the Nth one. So the
solution of equation (6) can be searched from the Nth
signal to the ith signal as layer by layer in a tree. That is
the principle of VBLAST algorithm. Each possible
transmit signal si is called a node in the searching tree.
The solution finding can be depicted as searching in the
tree from the root node to a cer tain leaf node.
VBLAST only searches the tree by one route. If there
is an error in one layer, signals in next layers will be er-
ror in high probability. That is why the performance of
VBLAST algorithm is not good enough. ML algorithm
searches all the leaf nodes in the tree and selects the node
which satisfies equation (6) from all the possible nodes.
Obviously it has the optimal performance, but is a NP-
hard problem.
To find the best signal as in equation (6), the distance
between transmit and receive symbol should be calcu-
lated. According to formula (5), the Euclidean distance
(ED) can be define d as
1
22
1
ˆ
NN
jjkk
jkj
Drs 










 (10)
Also define the partial Euclidean distance (PED) as
1
22
ˆ
NN
ijjkk
jik j
Drs 










 (11)
4. Schnorr-Euchner SD algorithm
Despite the optimal performance, the number of visited
nodes of ML algorithm is the exponential function of Nt
and m, where m is the signal modulation order. That is a
very large number, so the complexity is too high to be
utilized. SD algorithm reduces the number of visited
nodes by setting a hypersphere before search and only
nodes in this hypersphere will be searched. When a new
leaf node is found in the hypersphere, the radius of the
hypersphere is shrunk to the distance of this node. The
complexity of the SD is a small fraction of that of ML.
SESD is the most important SD algorithm. It optimizes
the SD algorithm by searching the smallest child node of
the parent node each layer first. The first found solution
is often the solution good enough. As a result, some
nodes visiting can be avoided and the calculation com-
plexity can be further lowered.
5. Pipeline Structure SESD Algorithm
The SESD algorithm must search the whole tree to get
the solution. Each visited node must compare with the
global smallest radius to determine whether or not it
should be kept. Where the SESD algorithm is used,
symbols should be detected one by one. Another detec-
tion can only begin after one is over. As a result, the av-
erage processing time can not drop easily.
In this article, we proposed that the whole search tree
can be divided into blocks and the search process can be
executed from block to block to form a pipeline structure,
like Figure 1. Each block is one part in the pipeline. The
number of block equals to the number of part in the pipe-
line. The whole search begins from one certain block.

X. Y. MAO ET AL.
110
Figure 1. Pipeline structure SESD algorithm tree.
The top node of blocks is called the sub-root node of
this block, from which the block search starts. Unlike the
tree root node which has no practical significance, the
sub-root node has its counterpart transmit signal and its
PED.
There is a solution for each part, which is called the
sub-solution of this part. The radius used in the SESD is
still the threshold to cut node in each part. All parts share
one radius although it should be updated anytime when
the update condition is satisfied. The radius is called
globe radius in our algorithm. Each sub-solution will
update the globe radius, which will act as the cutting ra-
dius in the remaining parts.
Because of the node cutting, there may be no sub-so-
lution for some parts. This is not so much a bad news as
a good news because that means all nodes in this part are
cut and the visited nodes number in this part is often
small. When a sub-solution in one part is found, the
globe radius will update to the ED of this sub-solution.
Each part executes independently except one input pa-
rameter and two output parameters. One input parameter
is the cutting radius, and the output parameters are the
new radius and the sub-solution of this part. So it can be
processed in a pipeline structure. Each part can process at
the same time. If the process of one part is over, it passes
the new radius and sub-solution to the next part and be-
gins a new process. There are several processes for de-
coding in one pipeline at the same time. The average
processing time for one detection will drop.
The structure of the proposed algorithm can be de-
picted as Figure 2(a). Each detection is divided into M
parts. One signal begins its step Kth detection at the time
when the previous signal ends its step Kth detection and
begins its step (K+1)th detection. So in a pipeline with M
parts, there are M signals detection at the same time, like
Figure 2(b).
As mentioned before, if the previously processed
block generates a radius small enough, most nodes in
following blocks will be cut quickly. Th e number of vis-
ited nodes will be small and the calculation complexity
will be low. So we can deduce that th e sequence of block
detection should be arranged in a way that the first de-
tected block should be the block that will most likely
generate the smallest sub-solution for the whole tree,
which is the final solution. So the sequence of block de-
tection should be arranged in the rising order of the PED
of the sub-root, that is, just the sequence of the SESD
algorithm.
6. Simulation Results
On the basis of section 5, we show the co mplexity of our
algorithm and the SESD algorithm. The performance of
the proposed algorithm is optimal as the performance of
SESD, so that it is not necessary to be shown. The com-
plexity is represented by the visited node number as in
[16].
The complexity of the proposed algorithm is compared
with the SESD algorithm in different SNRs. Also the
visited node numbers of every part are listed. We convert
the calculation into real field instead of complex field in
both figures. But all results are the same as in complex
field.
Figure 3 shows the complexity of a 4-by-4 antenna
system with 16QAM modulation. Figure 4 shows the
complexity of a 4-by-4 antenna system with 64QAM
modulation.
From both figures, it can be found that the sum of the
visited node number of all parts almost equals to that of
the SESD algorithm, which means that the proposed al-
gorithm does not increase the calculation complexity.
The average process time is determined by the part that
has the largest visited node number, which is the first
part. Specially, in 16QAM system of Figure 3, the aver-
age process time is about 48.77%, 54.34% or 60.18% of
that of the SESD algorithm when SNR=0, 10 or 20dB. In
(a)
(b)
Figure 2. Pipeline structure of SESD algorithm.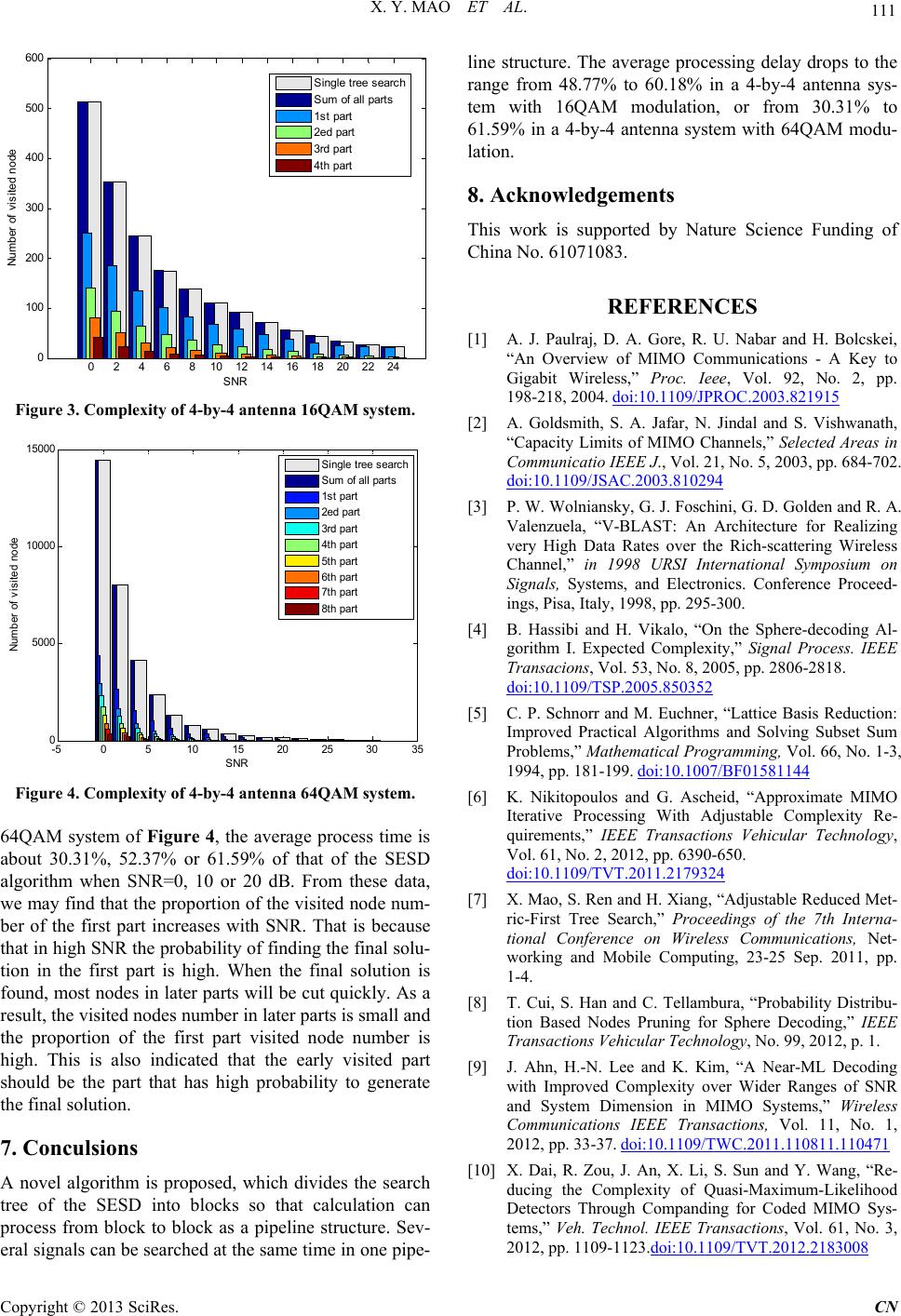

X. Y. MAO ET AL.
111
0 2 4 6 810 12 1416 18 20 2224
0
100
200
300
400
500
600
SNR
Number of visi ted node
Si ngl e t ree searc h
S um of all pa rts
1s t part
2ed part
3rd part
4th part
Figure 3. Complexity of 4-by-4 antenna 16QAM system.
-5 05 1015 20 25 30 35
0
5000
10000
15000
SNR
Num ber of v isit ed node
Si ngl e t ree s earc h
Sum of all part s
1s t part
2ed part
3rd part
4th part
5th part
6th part
7th part
8th part
Figure 4. Complexity of 4-by-4 antenna 64QAM system.
64QAM system of Figure 4, the average process time is
about 30.31%, 52.37% or 61.59% of that of the SESD
algorithm when SNR=0, 10 or 20 dB. From these data,
we may find that the prop ortion of the visited node num-
ber of the first part increases with SNR. That is because
that in high SNR the prob ability of finding the final so lu-
tion in the first part is high. When the final solution is
found, most nodes in later parts will be cut quickly. As a
result, the visited nodes number in later parts is small and
the proportion of the first part visited node number is
high. This is also indicated that the early visited part
should be the part that has high probability to generate
the final solution.
7. Conculsions
A novel algorithm is proposed, which divides the search
tree of the SESD into blocks so that calculation can
process from block to block as a pipeline structure. Sev-
eral signals can be searched at the same time in one pipe-
line structure. The average processing delay drops to the
range from 48.77% to 60.18% in a 4-by-4 antenna sys-
tem with 16QAM modulation, or from 30.31% to
61.59% in a 4-by-4 antenna system with 64QAM modu-
lation.
8. Acknowledgements
This work is supported by Nature Science Funding of
China No. 61071083.
REFERENCES
[1] A. J. Paulraj, D. A. Gore, R. U. Nabar and H. Bolcskei,
“An Overview of MIMO Communications - A Key to
Gigabit Wireless,” Proc. Ieee, Vol. 92, No. 2, pp.
198-218, 2004. doi:10.1109/JPROC.2003.821915
[2] A. Goldsmith, S. A. Jafar, N. Jindal and S. Vishwanath,
“Capacity Limits of MIMO Channels,” Selected Areas in
Communicatio IEEE J., Vol. 21, No. 5, 2003, pp. 684-702.
doi:10.1109/JSAC.2003.810294
[3] P. W. Wolniansky , G. J. Fosc hini, G. D. Golden and R. A.
Valenzuela, “V-BLAST: An Architecture for Realizing
very High Data Rates over the Rich-scattering Wireless
Channel,” in 1998 URSI International Symposium on
Signals, Systems, and Electronics. Conference Proceed-
ings, Pisa, Italy, 1998, pp. 295-300.
[4] B. Hassibi and H. Vikalo, “On the Sphere-decoding Al-
gorithm I. Expected Complexity,” Signal Process. IEEE
Transacions, Vol. 53, No. 8, 2005, pp. 2806-2818.
doi:10.1109/TSP.2005.850352
[5] C. P. Schnorr and M. Euchner, “Lattice Basis Reduction:
Improved Practical Algorithms and Solving Subset Sum
Problems,” Mathematical Programming, Vol. 66, No. 1-3,
1994, pp. 181-199. doi:10.1007/BF01581144
[6] K. Nikitopoulos and G. Ascheid, “Approximate MIMO
Iterative Processing With Adjustable Complexity Re-
quirements,” IEEE Transactions Vehicular Technology,
Vol. 61, No. 2, 2012, pp. 6390-650.
doi:10.1109/TVT.2011.2179324
[7] X. Mao, S. Ren and H. Xiang, “Adjustable Reduced Met-
ric-First Tree Search,” Proceedings of the 7th Interna-
tional Conference on Wireless Communications, Net-
working and Mobile Computing, 23-25 Sep. 2011, pp.
1-4.
[8] T. Cui, S. Han and C. Tellambura, “Probability Distribu-
tion Based Nodes Pruning for Sphere Decoding,” IEEE
Transactions Vehicular Technology, No. 99, 2012, p. 1.
[9] J. Ahn, H.-N. Lee and K. Kim, “A Near-ML Decoding
with Improved Complexity over Wider Ranges of SNR
and System Dimension in MIMO Systems,” Wireless
Communications IEEE Transactions, Vol. 11, No. 1,
2012, pp. 33-37. doi:10.1109/TWC.2011.110811.110471
[10] X. Dai, R. Zou, J. An, X. Li, S. Sun and Y. Wang, “Re-
ducing the Complexity of Quasi-Maximum-Likelihood
Detectors Through Companding for Coded MIMO Sys-
tems,” Veh. Technol. IEEE Transactions, Vol. 61, No. 3,
2012, pp. 1109-1123.doi:10.1109/TVT.2012.2183008

X. Y. MAO ET AL.
112
[11] B. Shim and I. Kang, “Sphere Decoding With a Probabil-
istic Tree Pruning,” Signal Process. IEEE Transactions,
Vol. 56, No. 10, 2008, pp. 4867-4878.
doi:10.1109/TSP.2008.923808
[12] X. Y. Mao, Y. X. Cheng, L. L. Ma and H. G. Xiang,
“Step Reduced K-best Sphere Decoding,” Proceedings of
the 76th IEEE Vehicular Technology Conference, Quebec
City, Canada, 3-6, Sep. 2012, pp. 1-4.
[13] J. W. Choi, B. Shim and A. C. Singer, “Efficient
Soft-Input Soft-Output Tree Detection via an Improved
Path Metric,” Inf. Theory Ieee Trans., Vol. 58, No. 3,
2012, pp. 1518-1533.
doi:10.1109/TIT.2011.2177590
[14] K. J. Choi and K. S. Kim, “Hierarchical Tree Search for
Runtime-Constrained Soft-Output MIMO Detection,”
IEEE Transactions Vehicular Technology, Vol. 62, No. 2,
2013, pp. 890-896. doi:10.1109/TVT.2012.2227868
[15] S.-L. Shieh, R.-D. Chiu, S.-L. Feng and P.-N. Chen,
“Low-Complexity Soft-Output Sphere Decoding with
Modified Repeated Tree Search Strategy,” IEEE Commu-
nications Letters, Vol. 17, No. 1, 2013, pp. 51-54.
doi:10.1109/LCOMM.2012.112012121728
[16] A. Schenk, R. F. H. Fischer and L. Lampe, “A Stopping
Radius for the Sphere Decoder and Its Application to
MSDD of DPSK,” Communications Letters, IEEE, Vol.
13, No. 7, 2009, pp. 465-467.
doi:10.1109/LCOMM.2009.090940