Journal of Intelligent Learning Systems and Applications, 2011, 3, 26-36
doi:10.4236/jilsa.2011.31004 Published Online February 2011 (http://www.SciRP.org/journal/jilsa)
Clustering-Inverse: A Generalized Model for
Pattern-Based Time Series Segmentation*
Zhaohong Deng1,2, Fu-Lai Chung2, Shitong Wang1,2
1School of Information, Jiangnan University, Wuxi, China; 2Department of Computing, Hong Kong Polytechnic University, Hong
Kong, China.
Received November 4th, 2010; revised January 5th, 2011; accepted January 19th, 2011
ABSTRACT
Patterned-based time series segmentation (PTSS) is an important task for many time series data mining applications.
In this paper, according to the characteristics of PTSS, a generalized model is proposed for PTSS. First, a new inter-
pretation for PTSS is given by comparing this problem with the prototype-based clustering (PC). Then, a novel model,
called clustering-inverse model (CI-model), is presented. Finally, two algorithms are presented to implement this
model. Our experimental results on artificial a nd real-world time series demonstrate that the proposed algorithms are
quite effective.
Keywords: Pattern-Based Time Series Segmentation, Clustering-Inverse, Dynamic Time Warping, Perceptually
Important Points, Evolution Compu tation, Particle Swarm Optimization, Genetic Algorith m
1. Introduction
With the large amounts of time series data arising from
various fields in recent years, the time series data mining
has emerged as an important research topic in the field of
data mining [1-3]. Especially, as one of the most funda-
mental tasks in time series data mining, the time series
segmentation has attracted extensiv e attention [4,5].
The conventional time series segmentation algorithms
can be classified into the following two main categories
[6]. The aim of the first category is to create a high level
representation of the time series for indexing, clustering,
and classification [7,8] and the aim of the second cate-
gory is to identify switching dynamics in time series
[9,10].
In addition to these two main categories of algorithms
mentioned above, a kind of novel pattern-based time se-
ries segmentation algorithm (PTSS) in [11] and its im-
proved versions [7,8] were developed to segment finan-
cial time series. The distinctive characteristic of PTSS is
that a pattern time series set (i.e. a pattern template set) is
given to control the segmentation. In the pattern time
series set, a pattern time series also represents a tech-
nique template, which indicates a representative time
series segment in a time series. For different practical
applications, the corresponding technique templates usually
represent the special meaning. The aim of PTSS is to
obtain the time series segments which are similar to a
certain pattern template in the given pattern time series
set. In this paper, we mainly focus on the study of PTSS.
In this study, by comparing PTSS with the proto-
type-based clustering (PC), we find that PTSS may be
interpreted as an inverse problem of PC. According to
this interpretation, a generalized model, called Cluster-
ing-Inverse model (CI-model), is proposed for PTSS.
Then, the main components and processing operations of
this model are discussed in detail. Furthermore, a de-
tailed algorithm is presented to put this model into prac-
tice. As the matching measure of time series is of funda-
mental importance in segmentation, we also propose a
new Perceptually Important Point (PIP) based Dynamic
Time Warping (DTW) measure by integrating PIP iden-
tification mechanism [12] with DTW measure [13]. The
advantage of the proposed measure is that it combines
the merits of both PIP mechanism and DTW simulta-
neously. To investigate the performance of the proposed
CI-model, we have applied the proposed algorithms to
the real-world time series.
*This study was supported in part by the Hong Kong Polytechnic Uni-
versity under Grant Z-08R, by the National Natural Science Foundation
of China under Grants 60773206, 60903100, 60975027 and 90820002,
by the Natural Science Foundation of Jiangsu province under Grant
BK2009067 and the Doctoral Foundation of Jiangnan University.

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 27
The contributions of this study can be summarized into
the following four aspects:
 Give a new interpretation for PTSS;
 Propose a generalized CI-model for PTSS;
 Propose a PIP-based DTW measure;
 Present an algorithm based on the CI-model.
The paper is organized as follows. In section 2, a for-
mal description and a new interpretation of PTSS are
given. The proposed CI-model is introduced and its main
components and processing operations are discussed in
section 3. Section 4 presents a detailed algorithm to real-
ize the proposed model. Experimental results are re-
ported in Section 5. The conclusions and some prospects
are given in section 6.
2. Description and New Interpretation about
PTSS
2.1. Description about PTTS
First, we give a formal description of PTSS (Pattern
based Time Series Segmentation). Given a time series

12 n
Ttttand a set of pattern time series, or pattern
templates,

 
12 ,1,2,,
i
Pii m
DPPpppi c ,
where i
m, n denote the lengths of i P and T, re-
spectively. The aim of PTTS is to segment T into a set
of k time series segments,

1,1,,
ii i
Siibb e
DSStttik

 .
In the set
s
D, each time series segment is similar to one
of the pattern template in
P
D, and meanwhile, the set
s
D must satisfy the constraint: 12 k TSS S, where
i
bis the beg inning position o f i S in T, 11b and i e
is the ending position of i S in T, k en.
The obtained time series segments i S from time se-
ries T by PTSS may have different lengths and can be
classified into different subgroups, which are associated
with the corresponding pattern templates. Th erefore, S D
may be described as12 c
s
PP P
DDD D, where



1,2, ,
|,max ,
j
Piijhc ih
DSsimSP simSP


;
1, 2,,ik; 1, 2,,jc;

sim denotes a similarity
measure between two time series.
2.2. New Interpretation about PTSS
In this subsection, we will discuss the relationship be-
tween PTSS and the prototype-based clustering (PC), and
then give a new interpretation for PTSS. PC can be ex-
pressed as the following problem: Given a dataset D
and the number c of its clusters, the aim of PC is to get
c optimal prototypes i V (e.g., cluster centers),
1, ,ic. The sample points associated with the same
prototype are as compact as possible while the sample
points associated with different prototypes are as scat-
tered through the data space as possible. Figure 1(a)
shows a simple illustration for PC. Correspondingly, we
also give an illustration for PTSS in Figure 1(b).
By comparing Figure 1(a) with Figure 1(b), it is easy
to find that the pattern template i P in Figure 1(b) can
be interpreted as a prototype i V in Figure 1(a). Mean-
while, the set of time series segments
s
D in Figure 1(b)
can be interpreted as the dataset D in Figure 1(a). The
essential difference between PC and PTSS lies in the fact
that given the dataset D, the aim of PC is to get the
optimal prototypes i V in PC by optimization learning,
while given the prototypes i P, the aim of PTSS is to
obtain the optimal dataset
s
D. Hence, we can give the
following interpretation: PTSS can be viewed as an in-
verse problem of PC and here we call it the cluster-
ing-inverse problem.
3. Clustering-Inverse: A Generalized Model
for PTSS
3.1. The Framework of the Proposed Model:
Clustering-Inverse
In terms of the interpretation in the above section, a ge-
neralized model, called clustering-inverse model (CI-
model), is proposed for PTSS. The framework of the
proposed model is shown in Figure 2 .
In Figure 2, Tdenotes the time series to be seg-
mented. The pattern time series set
P
D is the pattern
template set used as the constraints for the time series
segmentation. The initialization operation is to present
the initial segmentation point set which contains
s
segmentation points segmenting T into k time series
segments with 1ks

. The data processing operation
in Figure 2 is utilized to process the time series segment
set S
D and the pattern time series set
P
D. With a data
processing operation, S
D and
P
Dcan be transformed
into the corresponding datasets S
D and
P
D, which are
usually more suitable for computing the matching meas-
ures between the pattern templates and the obtained
Figure 1. The illustrations of (a) the prototype-based
clustering PC and (b) the pattern-based time series seg-
mentat ion PTSS .

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 28
Figure 2. The framework of the proposed CI model for
PTSS.
segment. Meanwhile, S D and
P
D can be taken as the
dataset and the prototype set for computing the objective
function
J
in Figure 2. The objective function
J
of
the prototype-based clustering is adopted as the optimi-
zation objective and the segmentation point set of time
series T, as the solution variable, will be updated by an
optimization method. In the optimization learning pro-
cedure,
P
D is always unchangeable and the aim of op-
timization is to obtain the optimal time series segment set
S
D of T.
3.2. The Main Components and Operations in
CI-Model
In this subsection, we discuss the main components and
operations in the proposed CI-model, including 1) the
objective function, 2) the optimization method, 3) the
data processing operation, 4) the matching measure, and
5) the initialization operation.
3.2.1. Objective Function
Many objective functions based on different principles
have been proposed for PC. In practice, according to the
analysis in section 2.2, almost all these objective func-
tions in PC are available for the proposed CI model. Here,
we only introduce four representative ones: the objective
function of K-means clustering, the objective function of
FCM clustering [14], the objective function of fuzzy
clustering neural network (FCNN) [15] and the objective
function of maximum entropy clustering (MEC) [16].
Now, we give a brief description of the four objective
functions.
K-means clustering is the most classical clustering al-
gorithm in PC. Its objective function can be expressed as

2
1,
i
c
Kmeansj i
ijI
JD

 xv (1)
where
j
x is the data vector; i v is the cluster center
vector (i.e. the cluster prototype); c is the number of
clusters;


,
j
i
Dxv denotes the dissimilarity measure
between
j
x and i v. The most commonly used dissi-
milarity measure in (1) is the Euclidean distance.
The famous FCM clustering is the fuzzy version of
K-means clusterig. Compared with K-means, it is more
robust to noisy environments in real applications. The
objective function of FCM clustering can be expressed as


2
11 ,
cN
m
FCMijj i
ij
JuD

 xv ,1 01, 1
c
ij ij
i
uu

 

(2)
where ij u denotes the fuzzy membership; 1m de-
notes the fuzzy index;


,
j
i
Dxv denotes the dissimi-
larity measure between
j
x and i v. The update rule of
the fuzzy membership ij
u in (2) can be form ulated as
 
21 21
1
,,
mm
c
ijj ij k
k
uD D



 

xvxv (3)
The FCNN clustering also utilizes the fuzzy concep-
tion, but the most important basis of FCNN clustering is
the neural-network learning. Its objective function can be
written as


2
11
exp ,
cN
FCNNijj i
ij
JuD



 xv
1
01, 1
c
ij ij
i
uu



 (4)
where ij
u denotes the corresponding fuzzy membership;


,
j
i
Dxv denotes the dissimilarity measure between
j
x and i v;

is a constant parameter. The update
rule of the fuzzy membership ij
u in (4) can be formu-
lated as





22
1
exp ,exp ,
C
ij jiji
k
uD D



 

xvxv
(5)
The MEC clustering is a typical algorithm of the
probability-theory based PC algorithms. Its objective
function can be expressed as


2
11 11
,ln
cN cN
M
ECijj iijij
ij ij
J
uDu u 
 

 
xv
1
01, 1
c
ij ij
i
uu



 (6)
where ij
u denotes the corresponding joint distribution
probability;

is a constant parameter;

,
j
i
Dxv de-
notes the dissimilarity measure. The update rule of ij
u
in (6) can be formulated as





22
1
exp ,exp ,
c
ij jiji
k
uD D



 

xvxv
(7)
The above four objective functions provide several

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 29
possible schemes to implement the proposed CI-model.
Note here that the objective functions in (1), (2) and (6)
are expected to achieve the minimum values, while the
objective functions in (4) is expected to achieve the
maximum value.
3.2.2. Optimization Meth o d
In the proposed CI-model, the objective function is just
the clustering objective function and the solution is the
segmentation point set

_int 12
,,,
s
eg pos
Dqqq, which
can be equivalently written as a vector

12
,,,
s
qq qq, where

11, 2,,1 ii
qqis
 ,
11q, s
qn; and n is the length of time series T.
Since the objective function usually can not be written as
an analytic expression of the solution

12
,,,
s
qq qq
directly, the traditional gradient optimization methods
and some other commonly used derivative-based opti-
mization methods are not suitable for this problem. Un-
der these conditions, the following optimization methods
can be considered.
1) Dynamic programming. It is the earliest technique
utilized to solve the traditional time series segmentation
problem [7]. A crucial step for dynamic programming
methods is to transform the optimization problem into its
corresponding dynamic programming equation. The
weakness of this kind of method for time series segmen-
tation is the high computational complexity. Meanwhile,
it is not a trivial problem to transform the optimization
process into its corresponding dynamic programming.
2) Random optimization. It is a simple method for the
time series segmentation [17]. This method first gives an
initial segmentation. Then, in the whole learning proce-
dure, the following operation is repeated: a segmentation
point is selected randomly to be replaced with an optimal
point obtained by trying all other potential segmentation
points. So the computational complexity is also quite
high like the dynamic programming method.
3 ) Evolutionary optimization. Evolutionary optimiza-
tion methods have been extensively studied and utilized
in various fields in recent years and their applications in
time series segmentation has been demonstrated in
[11,12]. Compared with the above two optimization me-
thods, the advantages of evolutionary optimization me-
thods are their easy use and high intelligence. Due to the
advantages of evolutionary optimization methods, in the
following algorithms presented to implement the pro-
posed CI-model, this kind of optimization methods is
adopted.
3.2.3. Data Pro cessi ng
Data processing is an important operation: 1) to trans-
form the time series segments and pattern time series into
easily processed data vectors; 2) to facilitate computing
the matching measures between the obtained time series
segments and the pattern time series. For example, the
transformation of the obtained time series segments and
the pattern time series into the corresponding vectors
with the same dimensional number will facilitate compu-
ting their matching measure using Euclidean distances; 3)
to effectively reduce the computational complexity of
matching measures. For example, the commonly used
DTW measure for time series matching needs to solve a
dynamic programming problem. With the increase of
time series length, the computation time of DTW meas-
ure will become very burdensome. Thereby, the data
processing is needed to improve the efficiency of DTW
measure.
In this study, to realize the above functions we intro-
duce the PIP (Perceptually Important Point) identifica-
tion mechanism [11,12] as a data processing operation in
CI. The PIP mechanism is to identify some perceptually
important points in time series to represent the time se-
ries. Thus the computational complexity is greatly de-
creased because the number of PIPs is far smaller than
the length of time series. Now we give a brief introduc-
tion to the PIP mechanism.
The idea of PIP identification is motivated by the fact
that a time series can be usually characterized by a few
important points. For example, the head-and-shoulder
pattern time series consists of a head point, two shoulder
points, and a pair of neck points. These points are per-
ceptually important in the human visual identification
process. Therefore, they can similarly be taken into ac-
count in the pattern matching process. Given a time se-
ries


12 n
X
xx x, its m PIPs can be obtained by the
following process. The first two PIPs that are found will
be the first and last points of
X
. The next PIP will be
the point in
X
with the maximum distance to the first
two PIPs. The fourth PIP will then be the point in
X
with maximum distance to its two adjacent PIPs, either
between the first and second PIPs or between the
second and the last PIPs. The process of locating the
PIPs continues until the number is equal to m. Figure
3 shows the process of identifying 7 PIPs from the
head-and-shoulder pattern time series with length
60n

.
3.2.4. Matc hi n g Mea s ure
The matching measure of times series is of fundamental
importance in time series data mining. The most com-
monly used measures are Euclidean distance and DTW
measure [13]. In [11,12] the PIP-based Euclidean dis-
tance was proposed, which revealed much better perfor-
mance in reducing the running time. Here, we first
briefly introduce the three matching measures, and then
propose a PIP-based DTW measure for time series
matc h i n g. Our purpose is to present a measure which can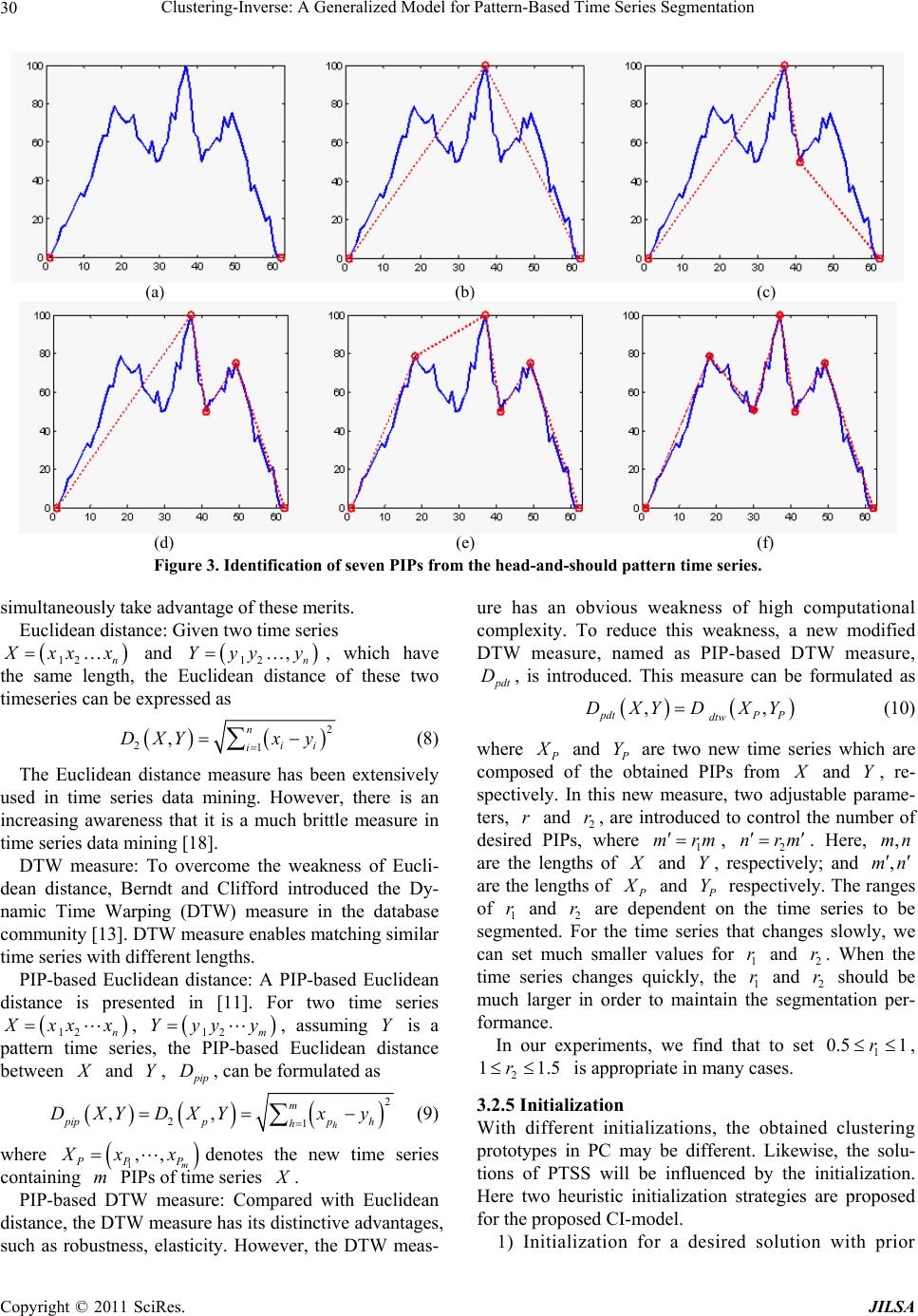

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 30
(a) (b) (c)
(d) (e) (f)
Figure 3. Identification of seven PIPs from the head-and-should pattern time series.
simultaneously take advantage of these merits.
Euclidean distance: Given two time series

12 n
X
xx x and

12 ,n
Yyy y, which have
the same length, the Euclidean distance of these two
timeseries can be expressed as
 
2
21
,n
ii
i
DXYx y


 (8)
The Euclidean distance measure has been extensively
used in time series data mining. However, there is an
increasing awareness that it is a much brittle measure in
time series data mining [18].
DTW measure: To overcome the weakness of Eucli-
dean distance, Berndt and Clifford introduced the Dy-
namic Time Warping (DTW) measure in the database
community [13]. DTW measure enables matching similar
time series with different lengths.
PIP-based Euclidean distance: A PIP-based Euclidean
distance is presented in [11]. For two time series

12 n
X
xx x,

12 m
Yyyy, assuming Y is a
pattern time series, the PIP-based Euclidean distance
between
X
and Y,
p
ip
D, can be formulated as

 
2
21
,, h
m
pippp h
h
DXYDXYxy


 (9)
where

1,,m
PP P
X
xxdenotes the new time series
containing m PIPs of time series
X
.
PIP-based DTW measure: Compared with Euclidean
distance, the DTW measure has its distinctive advantages,
such as robustness, elasticity. However, the DTW meas-
ure has an obvious weakness of high computational
complexity. To reduce this weakness, a new modified
DTW measure, named as PIP-based DTW measure,
p
dt
D, is introduced. This measure can be formulated as


,,
p
dtP P
dtw
DXYD XY (10)
where
P
X
and
P
Y are two new time series which are
composed of the obtained PIPs from
X
and Y, re-
spectively. In this new measure, two adjustable parame-
ters, r and 2 r, are introduced to control the number of
desired PIPs, where 1
mrm


, 2 nrm

. Here, ,mn
are the lengths of
X
and Y, respectively; and ,mn


are the lengths of
P
X
and
P
Y respectively. The ranges
of 1
r and 2 r are dependent on the time series to be
segmented. For the time series that changes slowly, we
can set much smaller values for 1
r and 2 r. When the
time series changes quickly, the 1
r and 2 r should be
much larger in order to maintain the segmentation per-
formance.
In our experiments, we find that to set 1
0.5 1r

,
2
11.5r

 is appropriate in many cases.
3.2.5 Initialization
With different initializations, the obtained clustering
prototypes in PC may be different. Likewise, the solu-
tions of PTSS will be influenced by the initialization.
Here two heuristic initialization strategies are proposed
for the proposed CI-model.
1) Initialization for a desired solution with prior

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 31
knowledge. With his knowledge, the user can specify the
approximate length dlen of the desired times series
segments. For example, given a stock index time series
with length 3000l taken from the daily closing price,
if the user wants to get the segments about a month pe-
riod or three-month period, he sets 30dlen

and
90 dlen , respectively. Correspondingly, 1sldlen


segmentation points can be initialized with the interval
dlen r, where
x


denotes the minimal integer which
is bigger than
x
and r is a random number to control
the initial interval between the adjacent segmentation
points. To set


0.75,1.25r is appropriate for most
cases.
2) Initialization evaluated by a specific performance
index. In some cases, little information can be used to set
dlen for initializing the segmentation points. In this
situation, we suggest to segment the time series by set-
ting different values of dlen , such as setting 100dlen

,
200dlen , and so on. Then, the appropriate initializa-
tion can be determined by a specific performance index
as the criterion.
4. CI-Model Based PTSS Algorithm
4.1. General CI-Model Based PTSS Algorithm
In this subsection, the general CI-model based algorithm
for PTSS is presented in Table 1.Evolutionary optimiza-
tion methods have their distinctive advantages, such as
much better global search ability. Among various evolu-
tionary optimization methods, Particle Swarm Optimiza-
tion (PSO) [20] is one of the most extensively studied
methods. In the following subsection, we will present
such a CI-model based PTSS algorithm using PSO.
4.2. PTSS Algorithm Based on CI-Model + SPSO
In this subsection, we introduce the PSO (Particle Swarm
Optimization) for CI-model to implement the PTSS. The
PSO is a population-based optimization method. The
PSO is motivated by the behavior of organisms such as
fishing schooling and bird flock. In a PSO system, each
individual is taken as a particle and a particle is taken as
a candidate solution to the problem at hand. Particles of
the population fly around in a multi-dimensional search
space, to find out an optimal or sub-optimal solution by
competition as well as by cooperation among them.
For simplicity, here, we directly use the well-known
Stand Particle Swarm Optimization (SPSO) as the opti-
mization method for CI model. First, we describe the
related important conceptions and search strategies of
SPSO. Then, a PTSS algorithm based on CI-model +
SPSO is presented.
4.2.1. Concept i ons about SPSO
In SPSO, the population contains
M
particles and the
thi particle can be described by two state variables: the
position vector


12
,,,
iii is
x
xxx and the velocity
vector


,, ,
iii s
vv vv. For the PTSS, the segmentation
vector


12
,,,
iii is
qq qq of the time series T can be
taken as the position variable of the thi particle. The
velocity variable i v of the thi particle is usually in-
itialized to be zero vector. In addition to these two state
variables of the thi particle, another state variable


,,
iiii
pp pp is utilized to describe the best posi-
tion the thi particle ever reached, which represents the
experience of the thi particle itself. The initial best
position variable


,,
iiii
pp pp of the thi par-
ticle is commonly set to ii px and can be updated by
the following rule when the aim of optimization is to
obtain the minimum value of objective function.
  





 



1
111
iii
i
iii
tifJtJt
ttifJtJt






pxp
pxxp
(11)
where t denotes the number of generations and


J

denotes objective function.
In SPSO, another very important variable is the global
best position variable
g
p, which describes the best posi-
tion among all the positions that all particles ever reached
and represents the social shared information. The global
best position
g
p is updated in every generation by the
following rule.

 
()
argmin
i
gi
t
tJtp pp (12)
4.2.2. E volution ary Rules of SPSO.
With the above con cepts, the evolutionar y rules of SPSO
can be described as
 

  
 
112 2
1
11
ijijij ijgj ij
ijij ij
vtwvtcpt xtcptxt
xtxt vt



 


(13)
where i denotes the thi particle; j denotes the
thj dimension; t denotes the tht generation; w
denotes the inertia weight, which often is set to be linear
decrease in a interval (e.g. [0.4, 0.9]); and 12
,cc are
two acceleration constants (often set in the interval
(0, 2]); 1

and 2

are two random numbers in the
interval


0 , 1. When a segmentation point vector i q
is taken as a position vector i
x in the SPSO, the con-
straint conditions



11
ij ij
xt roundxt (14)


 




11
1
11 1
ij
current current
ij ijij
ij ij
ij
x
t
xtifxtx andxtx
xt otherwise



 




(15)

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 32

1, 2,,
ij
x
n,

1
ij ij
xx

,

1, ,1js, 11
i
x,
is
x
n must be satisfied, where n is the length of the
time series to be segmented and
s
is the number of
segmentation points of a segmentation point vector, i.e.
the dimensional number of i
x. For the cons traint condi-
tions in PTSS, we need to make further processing on

1
ij
xtobtained by (14). where

round a denotes
the nearest integer to a; current
ij
x denotes the current
value of ij
x
; if current
ij
x has been updated in the tht
generation, thencurrent
ij
x

1
ij
xt, otherwise,

current
ij ij
x
xt, meanwhile, for simplicity, we set
01
current
i
x, (1)
curr ent
is
x
n
.
Based on the above conceptions and evolutionary rules
of the SPSO, a detailed PTSS algorithm based on the
CI-model +SPSO is presented in Table 2.
4.2.3. Some Disc ussi ons
In the above subsection, we present a PTSS algorithm
based on the CI-model. In fact, these two algorithms are
only two feasible schemes and can be furthermore im-
proved by different tactics.
In [11], an evolutionary PTSS algorithm is proposed
for financial time series segmentation and the corres-
ponding improved versions are presented in [12]. Here,
we give a brief discussion about the relationship between
these PTSS algorithms in [11,12] and the proposed
CI-model based PTSS algorithms in this study. In es-
sence, the algorithm in [11,12] optimizes the fitness ob-
jective function given in (16) by a GA optimizationme-
thod with the segmentation point set of the time series as
the solution.
Table 1. General CI-model based PTSS algorithm.
Step1
1) Given the time series to be segmented and the pattern
time series set.
2) Select a specific optimization objective function (e.g.
the objective function of FCM clustering) and the cor-
responding update rules of the related variables (e.g.
fuzzy membership variables in the FCM objective
function).
3) Select a matching measure of time series and the cor-
responding da ta processing operations.
4) Set the desired approximate segment length dlen
and initialize the segmentation point set with dlen .
5) Select the optimization method.
Step2 Use the selected optimization method to optimize the objective function and gain the optimal segmentation
point set.
Step3 Use the obtained optimal segmentation point set to get
the set of time series segments.
Table 2. PTSS algorithm based on CI-model + SPSO.
Step1
1) Given the time series to be segmented and the pattern
time series set.
2) Set the approximately desired segment lengthdlen.
3) Initialize the state variables of the populat i on.
4) Select the objective function and the corresponding
update rules of the variables in this objective function.
Step2
1) Select the matching measure and the corresponding
data processing operation.
2) Transform the pattern time series into the correspond-
ing prototype vectors by a data processing operation.
3) Set the termination conditions of the SPSO.
Step3 Obtain the time series segments sets associated with
different individuals, and then transform them into the
corresponding data sets.
Step4 Update the corresponding variables (e.g. the FCM mem-
bership variables).
Step5 Compute the objective function values of all individual s
Step6 If the termination conditions of the SPSO are satisfied,
then terminate the learning of the SPSO and go to Step 8;
Otherwise, go to Step 7
Step7 Generate the next generation population with the evolu-
tionary rules of the SPSO in (11)-(15); Then, go to Step 3.
Step8
Obtain the optimal individual, i.e. the optimal segmenta-
tion point vector. Furthermore, get the set of time series
segments associated with the optimal segmentation point
vector.
 
1
1k
s
j
j
f
itness DfitnessS
k
 (16)



min ,
i
jij
P
f
itness SDisP S

 (17)
where
j
S (1, 2,,jk

), i P (1, 2,,ic) are the
obtained time series segments and the pattern time series,
respectively,


Dis

denotes the dissimilarity distance
measure. Substituting (17) into (16), (16) can be refor-
mulated as


1
1,
P
i
c
s
ij
ijD
f
itnessD DisPS
k
 (18)
 


1,2, ,
,min ,
i
Pj jijh
hc
DSDisSPDisSP


,1,2,,ic


(19)
By comparing (18) with (1) (i.e. the objective func tion
of K-means clustering), we find that the two objective
functions are very similar if the same dissimilarity meas-
ure is adopted. The only difference is the coefficient 1k
in (18). In fact, the variable k only fluctuates in a nar-
row range by some parameter controls [11,12]. So the
presented algorithm in [11] can be approximately re-
garded as a special case of the proposed CI-model based
PTSS algorithms when the objective function of K-
means clustering and GA optimization method are
adopted for CI-model.
In the exiting time series segmentation algorithms, the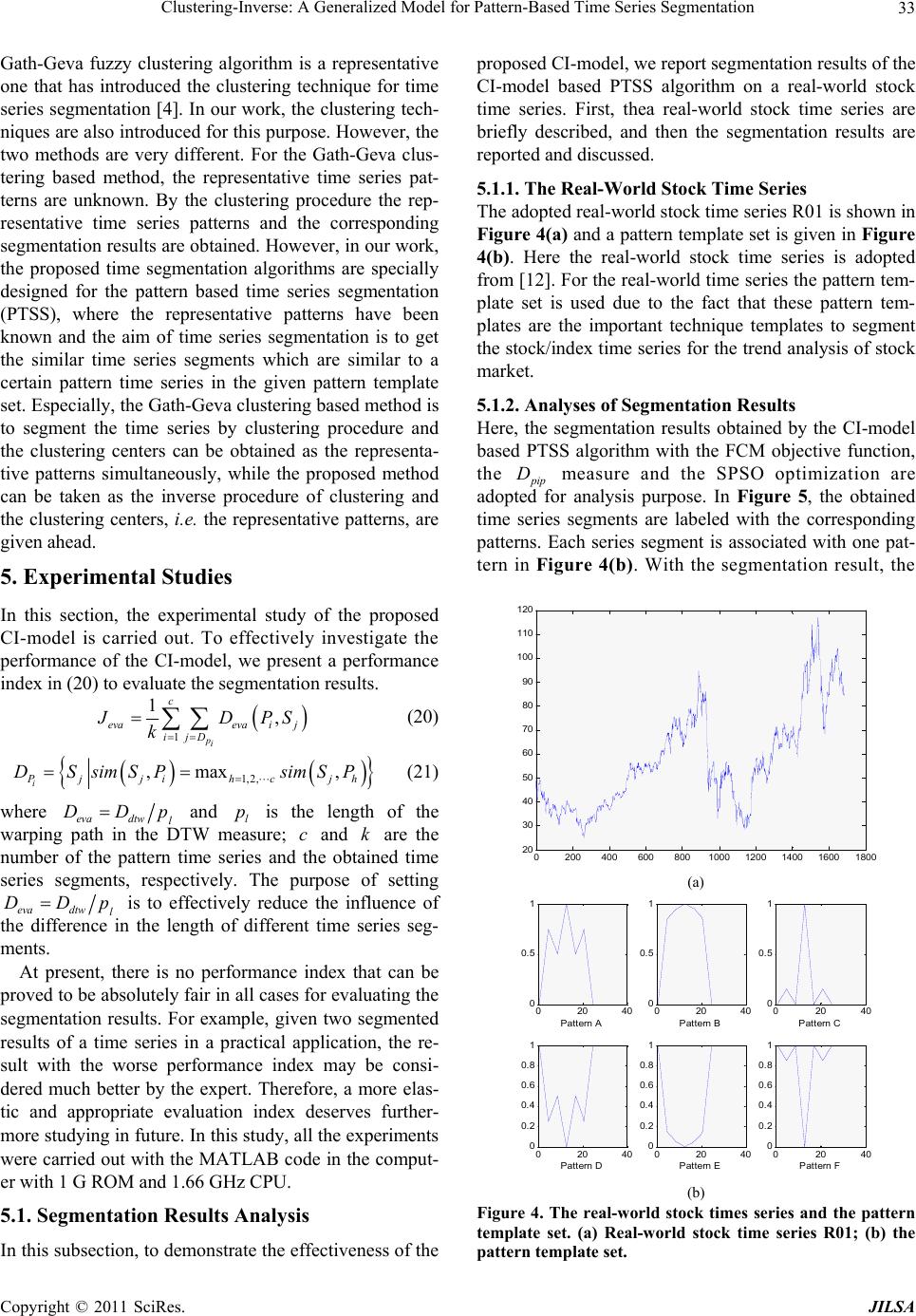

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 33
Gath-Geva fuzzy clustering algorithm is a representative
one that has introduced the clustering technique for time
series segmentation [4]. In our work, the clustering tech-
niques are also introduced for this purpose. However, the
two methods are very different. For the Gath-Geva clus-
tering based method, the representative time series pat-
terns are unknown. By the clustering procedure the rep-
resentative time series patterns and the corresponding
segmentation results are obtained. However, in our work,
the proposed time segmentation algorithms are specially
designed for the pattern based time series segmentation
(PTSS), where the representative patterns have been
known and the aim of time series segmentation is to get
the similar time series segments which are similar to a
certain pattern time series in the given pattern template
set. Especially, the Gath-Geva clustering based method is
to segment the time series by clustering procedure and
the clustering centers can be obtained as the representa-
tive patterns simultaneously, while the proposed method
can be taken as the inverse procedure of clustering and
the clustering centers, i.e. the representative patterns, are
given ahead.
5. Experimental Studies
In this section, the experimental study of the proposed
CI-model is carried out. To effectively investigate the
performance of the CI-model, we present a performance
index in (20) to evaluate the segmentation results.

1
1,
pi
c
evaeva ij
ijD
J
DPS
k
 (20)
 

1,2,
,max ,
i
Pjjihc jh
DSsimSP simSP


 (21)
where evadtw l DDp and l p is the length of the
warping path in the DTW measure; c and k are the
number of the pattern time series and the obtained time
series segments, respectively. The purpose of setting
evadtwl
DDp is to effectively reduce the influence of
the difference in the length of different time series seg-
ments.
At present, there is no performance index that can be
proved to be absolutely fair in all cases for evalu ating the
segmentation results. For example, given two segmented
results of a time series in a practical application, the re-
sult with the worse performance index may be consi-
dered much better by the expert. Therefore, a more elas-
tic and appropriate evaluation index deserves further-
more studying in future. In this study, all the experiments
were carried out with the MATLAB code in the comput-
er with 1 G ROM and 1.6 6 GHz CPU.
5.1. Segmentation Results Analysis
In this subsection, to demonstrate the effectiv eness of the
proposed CI-model, we report segmentation results of the
CI-model based PTSS algorithm on a real-world stock
time series. First, thea real-world stock time series are
briefly described, and then the segmentation results are
reported and discussed.
5.1.1. The Real-World Stock Time Series
The adopted real-world stock time series R01 is shown in
Figure 4(a) and a p attern template set is given in Figure
4(b). Here the real-world stock time series is adopted
from [12]. For the real-world time series the pattern tem-
plate set is used due to the fact that these pattern tem-
plates are the important technique templates to segment
the stock/index time series for the trend analysis of stock
market.
5.1.2. Analyses of Segmentation Results
Here, the segmentation results obtained by the CI-model
based PTSS algorithm with the FCM objective function,
the
p
ip
D measure and the SPSO optimization are
adopted for analysis purpose. In Figure 5, the obtained
time series segments are labeled with the corresponding
patterns. Each series segment is associated with one pat-
tern in Figure 4(b). With the segmentation result, the
0200 400 6008001000 1200 1400 1600 1800
20
30
40
50
60
70
80
90
100
110
120
(a)
020 40
0
0. 5
1
Pattern A020 40
0
0. 5
1
Pattern B020 40
0
0. 5
1
Pattern C
020 40
0
0. 2
0. 4
0. 6
0. 8
1
Pattern D020 40
0
0. 2
0. 4
0. 6
0. 8
1
Pattern E020 40
0
0. 2
0. 4
0. 6
0. 8
1
Pattern F
(b)
Figure 4. The real-world stock times series and the pattern
template set. (a) Real-world stock time series R01; (b) the
pattern template set.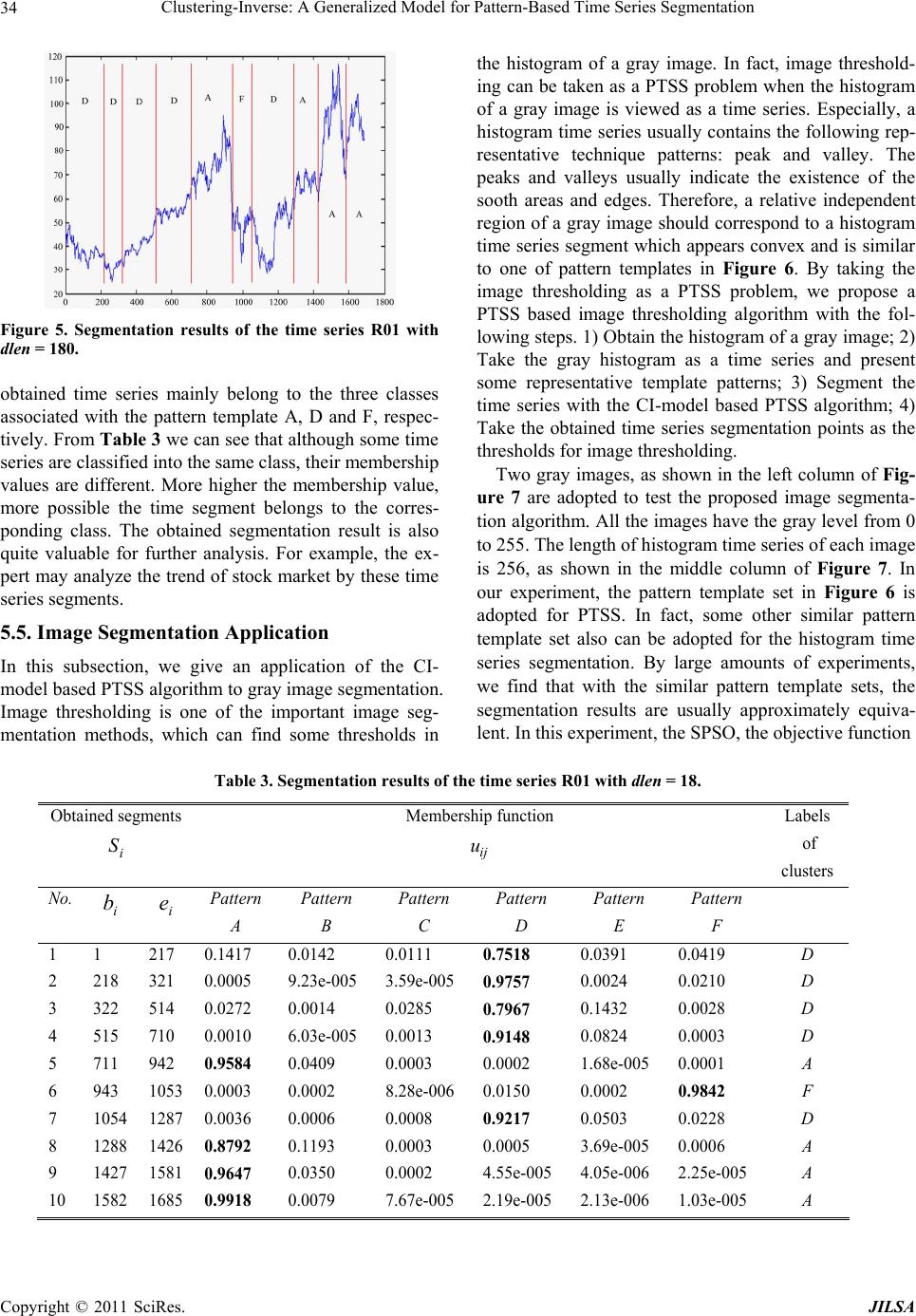

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 34
Figure 5. Segmentation results of the time series R01 with
dlen = 180.
obtained time series mainly belong to the three classes
associated with the pattern template A, D and F, respec-
tively. From Table 3 we can see that although some time
series are classified into the same class, their membership
values are different. More higher the membership value,
more possible the time segment belongs to the corres-
ponding class. The obtained segmentation result is also
quite valuable for further analysis. For example, the ex-
pert may analyze the trend of stock market by these time
series segments.
5.5. Image Segmentation Application
In this subsection, we give an application of the CI-
model based PTSS algorithm to gray image segmentation.
Image thresholding is one of the important image seg-
mentation methods, which can find some thresholds in
the histogram of a gray image. In fact, image threshold-
ing can be taken as a PTSS problem when the histogram
of a gray image is viewed as a time series. Especially, a
histogram time series usually contains the following rep-
resentative technique patterns: peak and valley. The
peaks and valleys usually indicate the existence of the
sooth areas and edges. Therefore, a relative independent
region of a gray image should correspond to a histogram
time series segment which appears convex and is similar
to one of pattern templates in Figure 6. By taking the
image thresholding as a PTSS problem, we propose a
PTSS based image thresholding algorithm with the fol-
lowing steps. 1) Obtain the histogram of a gray image; 2)
Take the gray histogram as a time series and present
some representative template patterns; 3) Segment the
time series with the CI-model based PTSS algorithm; 4)
Take the obtained time series segmentation points as the
thresholds for image thresholding.
Two gray images, as shown in the left column of Fig-
ure 7 are adopted to test the proposed image segmenta-
tion algorithm. All the images h ave the gray level from 0
to 255. The length of histogram time series of each image
is 256, as shown in the middle column of Figure 7. In
our experiment, the pattern template set in Figure 6 is
adopted for PTSS. In fact, some other similar pattern
template set also can be adopted for the histogram time
series segmentation. By large amounts of experiments,
we find that with the similar pattern template sets, the
segmentation results are usually approximately equiva-
lent. In this experiment, the SPSO, the objective function
Table 3. Segmentation results of the time series R01 with dlen = 18.
Obtained segments
i
S
Membership function
ij
u
Labels
of
clusters
No.
i
b
i
e Pattern
A
Pattern
B
Pattern
C
Pattern
D
Pattern
E
Pattern
F
1 1 217 0.1417 0.0142 0.0111 0.7518 0.0391 0.0419 D
2 218 321 0.0005 9.23e-005 3.59e-005 0.9757 0.0024 0.0210 D
3 322 514 0.0272 0.0014 0.0285 0.7967 0.1432 0.0028 D
4 515 710 0.0010 6.03e-005 0.0013 0.9148 0.0824 0.0003 D
5 711 942
0.9584 0.0409 0.0003 0.0002 1.68e-005 0.0001 A
6 943 1053 0.0003 0.0002 8.28e-006 0.0150 0.0002 0.9842 F
7 1054 1287 0.0036 0.0006 0.0008 0.9217 0.0503 0.0228 D
8 1288 1426
0.8792 0.1193 0.0003 0.0005 3.69e-005 0.0006 A
9 1427 1581
0.9647 0.0350 0.0002 4.55e-005 4.05e-006 2.25e-005 A
10 1582 1685
0.9918 0.0079 7.67e-005 2.19e-005 2.13e-006 1.03e-005 A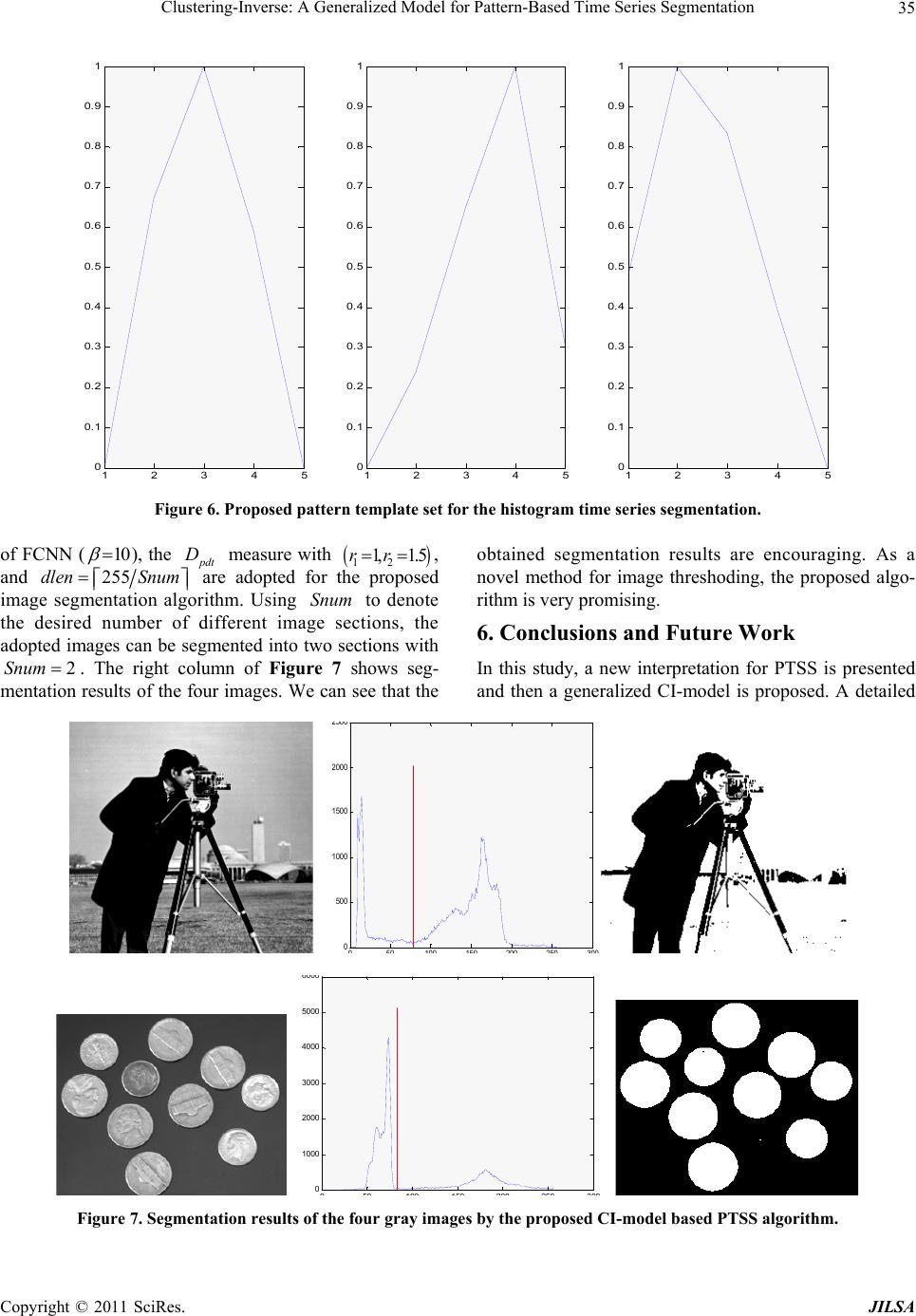

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 35
12 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1 23 45
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
12 3 4 5
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Figure 6. Proposed pattern template set for the histogram time series segmentation.
of FCNN (10

), the
p
dt
D measure with

12
1, 1.5rr,
and 255dlen Snum

are adopted for the proposed
image segmentation algorithm. Using Snum to denote
the desired number of different image sections, the
adopted images can be segmented into two sections with
2Snum. The right column of Figure 7 shows seg-
mentation results of the four imag es. We can see that the
obtained segmentation results are encouraging. As a
novel method for image threshoding, the proposed algo-
rithm is very promising.
6. Conclusions and Future Work
In this study, a new interpretation for PTSS is presented
and then a generalized CI-model is proposed. A detailed
0
50
100
150
200
250
300
0
500
1000
1500
2000
2500
0
50
100
150
200
250
300
0
1000
2000
3000
4000
5000
6000
Figure 7. Segmentation results of the four gray images by the proposed CI-model based PTSS algor ithm.

Clustering-Inverse: A Generalized Model for Pattern-Based Tim e Series Segmentation 36
algorithm is proposed to implement this model. The
proposed CI-model deserves furthermore studying on
many aspects in future, such as the objective functions,
the optimization methods, and so on. Moreover, it is also
very attractive to apply the proposed CI-model based
PTSS algorithms to other research fields. For example,
by integrating CI-model with the biomedicine knowledge,
the proposed algorithms can be adopted to analyze the
biomedicine signal.
Although the proposed CI-model for PTSS has shown
a promising performance, it still has the following dis-
advantage. The proposed CI-model based PTSS algo-
rithms usually need more parameters to implement time
series segmentation. For example, when the
p
dt
D meas-
ure is adopted two parameters for control the number of
the selected PISs are required. In order to make the pro-
posed CI-model based PTSS algorithms more efficient,
the further study for the choices of these parameters is
very valuable.
REFERENCES
[1] D. Gubbins, “Time Series Analysis and Inverse Theory
for Geophysicists,” Cambridge University Press, New
York, 2004.
[2] J. Kennedy and R. C. Eberhart, “A Discrete Version of
the Particle Swarm Algorithm,” Proceedings of the Con-
ference on Systems, Man and Cybernetics, Orlando, 12-15
October 1997, pp. 4104-4109.
[3] S. D. Kim, J. W. Lee, J. W. Lee and J. Chae, “A
Two-Phase Stock Trading System Using Distributional
Differences,” Lecture Notes in Computer Science, Vol.
2453, 2002, pp. 399-423. doi:10.1007/3-540-45801-8_39
[4] J. Abonyi, B. Feil, S. Nemeth and P. Arva, “Modified
Gath-Geva Clustering for Fuzzy Segmentation of Multi-
variate Time-Series,” Fuzzy Sets and Systems, Vol. 149,
No. 1, 2005, pp.39-56. doi:10.1016/j.fss.2004.07.008
[5] S. W. Kim and B. S. Jeong, “Performance Bottleneck of
Subsequence Matching in Time-Series Databases: Ob-
servation, Solution, and Performance Evaluation,” Infor-
mation Sciences, Vol. 177, No. 22, 2007, pp. 4841-4858.
doi:10.1016/j.ins.2007.06.032
[6] E. Keogh and S. Kasetty, “On the Need for Time Series
Data Mining Benchmarks: A Survey and Empirical
Demonstration,” Data Mining and Knowledge Discovery,
Vol. 7, No. 4, 2002, pp. 349-371. doi:10.1023/A:1024988
512476
[7] R. Bellman, “On the Approximation of Curves by Line
Segments Using Dynamic Programming,” Communica-
tions of the ACM, Vol. 4, No. 6, 1961, p. 284. doi:10.11
45/366573.366611
[8] J. Himberg, K. Korpiaho, H. Mannila, J. Tikanmaki and
H. T. T. Toivonen, “Time-Series Segmentation for Con-
text Recognition in Mobile Devices,” Proceedings of
IEEE Conference on Data Mining, 2001, pp. 203-210.
doi:10.1109/ICDM.2001.989520
[9] C. L. Fancoua and J. C. Principe, “A Neighborhood Map
of Competing One Step Predictors for Piecewise Seg-
mentation and Identification of Time Series,” Proceed-
ings of IEEE International Conference on Neural Net-
works, 1996, pp. 1906-1911.
[10] L. Feng, K. Ju and K. H. Chon, “A Method for Segmen-
tation of Switching Dynamic Modes in Time Series,”
IEEE Transactions on Systems, Man and Cybernetics,
Part B: Cybernetics, Vol. 35, No. 5, 2005, pp. 1058-1064.
doi:10.1109/TSMCB.2005.850174
[11] T. C. Fu, F. L. Chung, V. Ng and R. Luk, “Evolutionary
Segmentation of Financial Ti me Series into Subsequences,”
Proceedings of 2001 Congress on Evolutionary Compu-
tation, Seoul, 27-30 May 2001, pp. 426-430.
[12] F. L. Chung, T. C. Fu, V. Ng and R. Luk, “An Evolutio-
nary Approach to Pattern-Based Time Series Segmenta-
tion,” IEEE Transactions on Evolutionary Computation,
Vol. 8, No. 5, 2004, pp. 471-489. doi:10.1109/TEVC.20
04.832863
[13] D. Berndt and J. Clifford, “Using Dynamic Time Warp-
ing to Find Patterns in Time Series,” Proceedings of
AAAI-94 Workshop on Knowledge Discovery in Data-
bases, 1994, pp. 229-248.
[14] M. Sato, Y. Sato and L. C. Jain, “Fuzzy Clustering Mod-
els and Applications,” Physica-Verlag, New York, 1997.
[15] D. Zhang and S. K. Pal, “A Fuzzy Clustering Neural
Networks System Design Methodology,” IEEE Transac-
tions on Neural networks, Vol. 11, 2002, pp. 1174-1177.
doi:10.1109/72.870048
[16] C. Wang and S. Wang, “Supporting Content-Based
Searches on Time Series via Approximation,” Proceed-
ings of the 12th International Conference on Scientific
and Statistical Database Management, Berlin, 26-28 July
2002, pp. 69-81.
[17] J. Himberg, K. Korpiaho, H. Mannila, J. Tikanmaki and
H. T. T. Toivonen, “Time-Series Segmentation for Con-
text Recognition in Mobile Devices,” Proceedings of
IEEE Conference on Data Mining, 2001, pp. 203-210.
doi:10.1109/ICDM.2001.989520
[18] G. Kollios, M. Vlachos and G. Gunopulos, “Discovering
Similar Multidimensional Trajectories,” Proceedings of
18th International Conference on Data Engineering,
2002.