Communications and Network, 2013, 5, 86-92
http://dx.doi.org/10.4236/cn.2013.53B2017 Published Online September 2013 (http://www.scirp.org/journal/cn)
Quasi-cyclic Random Projection Code and Hardware
Implementation*
Saifeng Shi1, Min Wang1,2, X in lu Lu1, J un Wu1
1College of Electronics and Information Engineer ing, Tongji University, Shanghai, China
2School of Mathematics and Computer Science, Gannan Normal University, Ganzhou, China
Received May, 2013
ABSTRACT
Random Projection Code (RPC) is a mechanism that combines channel coding and modulation together and realizes
rate adaptation in the receiving end. Random projection code’s mapping matrix has significant influences on decoding
performance as well as hardware implementation complexity. To reduce hardware implementation complexity, we de-
sign a quasi-cyclic mapping matrix for RPC codes. Compared with other construction approaches, our design gets rid of
data filter component, thus redu cing chip area 728 4.95 um2, and pow er con sumption 331.4 6 uW in 0.13 um fabrication.
Our simulation results show that our method does not cause any performance loss and even gets 0.2 dB to 0.5 dB gain
at BER 10-4.
Keywords: Quasi-cyclic; Mapping Matrix; Random Projection Code; Hardware Implementation
1. Introduction
Rate adaptation plays a critical role in modern wireless
communications because channel conditions are dynamically
changed in a wide range. The physical layer in wireless
systems mainly consists of channel coding and modula-
tion, where actual transmission rate is adju sted by setting
rate of channel coding and constellation points of modulation
[2,3]. These approaches have two long-standing problems.
First, it is difficult to get the accurate channel state
information (CSI) due to inaccurate channel estimation
and feedback delay of estimated CSI. Second, there are
only limited combinations of coding rate and modulation
scheme, thus transmission rate can be adjusted only at a
stepwise way, which is not able to fully use channel
capacity. The work in [1] has exhibited a fast decoding
algorithm as a modulated coding scheme for seamless
rate adaptation in wireless communication.
For hardware architecture design, two main architect-
tures of LDPC hardware decoder are full-parallel decod-
ing and partial-parallel decoding. [6,7] have given a
typical low density parity check code (LDPC) decoder
architecture, including a data input buffer module, a set
of variable node processor, a group of check nodes proc-
essor, a decision module, the corresponding storage con-
trol module and a data output caching module. In full-
parallel architecture, each column and each row of the
parity check matrix is mapped to a different processing
unit and all these pro cessing units operate in parallel [8].
While in partial-parallel decoding [9], the parity check
matrix is partitioned into some non-overlap regions so
that a set of check nodes and variable nodes are updated
per cycle. [10] has given pipelined hardware imple-
mentation architecture of LDPC codes to achieve high
data throughput rate.
Similar to LDPC codes, the structure of mapping ma-
trix directly determines the hardware implementation
complexity of RPC codes. Belief propagation decoding
algorithm can achieve optimal performance in a Tanner
graph, because short girth affects the independence of
information transmission which can reduce the decode
performance. Meanwhile, the more randomized the non-
zero weights distribution is, the better decoding per-
formance is. Min et al [1] has proposed a multilevel cy-
clic-shift approach to generate the mapping matrix which
can facilitate the partial-parallel RPC decoding architect-
ture. Cui et al [4] has also proposed a method that ran-
domly exchanging columns of sub matrices, and then
stacking all the randomly generated sub matrices. At
simulation stage, the two methods have similar bit error
rate (BER) and throughput rate. While in hardware im-
plementation, there are two or more kinds of non-zero
weights in one sub-matrix, which will increase the hard-
ware implementation complexity.
In order to design a good mapping matrix, we design a
quasi-cyclic matrix, which can be suitable for hardware
*This work is financially supported by NSFC General Program under
contract No.6117304 1 .
C
opyright © 2013 SciRes. CN

S. F. SHI ET AL. 87
module partition, avoid access conflict of memory read
and write, simplify probability information transmission
in the iteration process, and not cause decoding performance
loss. The cyclic-shift times of each sub-matrix are
computed by two parameters and every sub-matrix is
only corresponding to one non-zero weighting. The
simulation results prove that quasi-cyclic matrix has
certain SNR gain compared to the cyclic-shift and the
randomly-shift approaches in random projection code
when BER is 10-4. As for hardware architecture design,
almost all the existing structures are match to a fixed
dimension matrix. Therefore, our hardware architecture
research is mainly focused on designing a new mapping
matrix which has better decoding performance without
changing the hardware architecture. For flexible hard-
ware implementation [5], we propose a configurable
architecture using wishbone bus to initialize registers and
memory bits before decoding, which can support different
dimensions of mapping matrix and weights.
The rest of this paper is organized as follows. Section
II gives the hardware architecture and the former con-
structions of mapping matrices. Section III introduces
our quasi-cyclic matrix construction method. Section IV
presents the hardware implementation results. The ana-
lyses of decoding performance and simulation results are
included in Section V. Finally, Section VI concludes this
paper.
2. Hardware Architecture
In this section, we first give the hardware architecture of
random projection code decoder. After that, we discuss
the construction of random permutation matrix and mul-
tilevel cyclic-shift matrix. Meanwhile, we analyze the
shortcomings brought by the two methods above.
2.1. Log-domain RPC and Hardware
Architecture
In practical wireless systems, the fast message passing
algorithms for channel codes typically use log lik elihood
ratio (LLR) as messages rather than probability and
likelihood ratio (LR). It can convert multiplications of
messages to additions, which significantly reduces the
decoding computation.
In our previous work, we convert the decoding algo-
rithm from arithmetic domain to log-domain [1]. And we
build look-up-table to solve the computationally inten-
sive problem of convolution. We have designed a partial-
parallel hardware decode architecture as well. The map-
ping matrix is partitioned into non-overlap regions
as Figure 1. Each memory bank module is connected to
a random address generator (RAG), a horizontal unit
processor (HUP) and a vertical unit processor (VUP)
which accommodates a
LL
N
LNL block of the
N
N

dimension mapping matrix.
Figure 1. Partial-parallel decoding hardware architecture.

S. F. SHI ET AL.
88
2.2. Former Mapping Matrix Design of RPC
Cui et al [4] has proposed a weight table 

1, 2, 4, 4
2
A4 A
for the non-zero weights of mapping matrix. First, they
construct three elementary matrices , and .
Each elementary matrix’s dimension is
1
A
N
8N4. The
structure of is shown as follows. Matrices and
have the same structure.
4
A1 A
2
A
4
84
4421
2144
04412
1244
2
4444
44
() () ()()
()()() ()
() ()()()
()() () ()
N
N
NN
A
AAAA
AAAA
GAAAA
AAAA





























Then it form a
N
2N matrix G0 by stacking random
permutation of the elementary matrices. Finally, two G0
are combined to form the
N
N matrix.
We call this construction method as random permutation.
The prominent feature is that the elementary matrices are
fully randomized in columns, which may bring perfor-
mance gain. However, from the hardware design and
implementation perspective, it will cause memory access
collisions among different parallel modules. The reason
is that the column number of two elements in one row
may be in [1:N8 ] or [N 81:N4].
To avoid the memory access collisions, min et al [1]
proposed multilevel cyclic-shift construction method.
The difference between the two methods is how to con-
struct the elementary matrix. They first generate two
identity matrices with
N
8N8 dimension, denoted by
1 and , respectively. Then two breakpoints
i
A2
i
Ai
p
and j
p
in
N
8 length are randomly selected. The col-
umns of sub matrix are permutated according to the seq
iji j
N
p
:,p:p1,1:p1
8
seq  


'
Two permutated matrices 12
i
are created.
Next, matrix is formed by concatenating matrices
12
. Finally, the elementary matrix
'
i
Aand A
'
i
A
'
i
'
i
Aand A ()
i
A

can
be created by random replacing the two 1’s on each row
with a pair of + i and – i.
For multilevel cyclic-shift construction method, the
data filter modules in Figure 1 are required to sort data
from memory banks. Because that the order of data must
consistent with the looking-up table storied in HUP.
Figure 2 describes the process of sorting data in RTL
realization. needs data vector which except the
data, i.e., ij
HUP

th
j

'
q12 j1j18 q,q ,,q,q,,q


'
q, to run con- volution operator. The should be allocated according
to the weights set w = {-4, -4, -2, -1, 1, 2, 4, 4}.
The simulation results show that the BER performance
and the data throughput rate of the two approaches in
AWGN channel and fading channel are close. No matter
for random permutation matrix or multilevel cyclic-shift
matrix, there are one or two different weights corre-
sponding to one HUP module. We find that HUP module
need store two looking-up tables, which are used to per-
form the probability convolution. In addition, the data
filter module is required to sort the iterative probability
information in the hardware architecture as Figure 2.
However, sorting data in hardware is very complicated.
For the architecture described in Figure 1, it will con-
sume amount of storage and computing resource. The
area and power consumption of the data filter will be
illustrated in section IV. Therefore, we expect that only
one weight corresponding to a sub matrix in partial-par-
allel hardware architecture.
3. Quasi-cyclic Mapping Matrix Design
Due to the complicated data sorting operation, we want
to find a new approach to generate mapping matrix of
RPC which facilitates hardware implementation. This
section mainly focuses on our quasi-cyclic mapping ma-
trix design. But we should guarantee that any modifica-
tion or new design of mapping matrix should not incur
any performance degradation. The two most important
metrics for performance are bit error rate and data
throughput rate. On the basis of the partial-parallel ar-
chitecture, our sub matrix has dimension
N
LNL

.
Then we assemble LL

sub matrices together to form
N
N

mapping matrix. Here we assume L=8. Detailed
design processes are described as follows.
First, we generate
N
8N8 dimension diagonal
identity matrix A.
NN
88
10 00 00
01 00 00
000 00
A00 000
00 00 10
00 00 01










Second, we adopt the quasi-cyclic method to acquire
the column permutation rules, which contains the right
cyclic-shift of each sub matrix. Here, we set two parameters
Figure 2. Data filter of probability information.

S. F. SHI ET AL. 89
x and y, and the times of right cyclic-shift for each sub matrix is listed below.
1xx^2 x^3x^4 x^5x^6 x^7
1*y x*yx^2*y x^3*yx^4*y x^5*yx^6*yx^7*y
1*y^2x*y^2x^2*y^2x^3*y^2x^4*y^2x^5*y^2x^6*y^2x^7*y^2
1*y^3 x*y^3 x^2*y^3 x^3*y^3 x^4*y^3 x^5*y^3 x^6*y^3 x^7*y^3
index 1*y^4x*y^4x^2*y^4x^3*y^4
1* y^5x *y^5

88
x^4*y^4 x^5*y^4 x^6*y^4 x^7*y^4
x^2*y^5 x^3*y^5 x^4*y^5 x^5*y^5 x^6*y^5 x^7*y^5
1*y^6 x*y^6 x^2*y^6 x^3*y^6 x^4*y^6 x^5*y^6 x^6*y^6 x^7*y^6
1*y^7 x*y^7 x^2*y^7 x^3*y^7 x^4*y^7 x^5*y^7 x^6*y^7 x^7*y^7










After every identity matrix A has right cyclic shifted
according to the corresponding element in index matrix,
for example the and are showed in Figure 3,
we can get the binary domain mapping matrix .
11
A12 A
*
G
11 1218
21 22
ij
*
77 78
818788 88
AA A
AA
A
G
AA
AAA
























Third, to cover all the non-zero weights combination
cases in a line of horizontal process units of random pro-
jection code, we generate a non-zero weights set W of
the
N
N dimension mapping matrix. In each row and
each column of W, eight weights{-4,-4,-2,-1,1,2,4,4}are
included.
88
44 442 211
221 144 44
44441122
11 22444 4
W22444 411
44 2211 44
11444422
441122 44

 




 






 

 

 





Finally, the weights vector table W is mapped to the
binary domain mapping matrix , . So, we
get the non-binary domain mapping matrix for random
projection code. Supposing the parameters
*
G*
ijij ij
GG*W

x2

, y3

and
N
400, then we get a dimension map-
ping matrix as Figure 4. 400400
010 20 30 40 50 60 70 8090 100
0
10
20
30
40
50
nz = 100
Figure 3. QC shift elementary matrices.
From the construction process above, we find that
there is only one weight in every sub matrix. In each row
of the mapping matrix, the order of weights is certain. So
the data filter can be avoided, which can reduce hardware
area and power consumption of decoder. Our simulation
results show that it does not bring performance degrada-
tion. The reduced hardware resources and decoding
throughput are listed in section IV. The detailed per-
formance analysis is presented in the section V.
4. Hardware Implementation
The log-domain RPC and the partial-parallel hardware
architecture have been realized using VHDL. For data
filter module, we use Synopsys design compiler with
0.13 um library for synthesis. The hardware area of a
data filter is 7284.95 um2, and the power consumption is
331.46 uW. Here we set clock frequency as 300 MHz in
our timing analysis.
However, in our new design, we use the proposed
quasi-cyclic mapping matrix in our hardware implementa-
tion. Therefore, the data filter can be completely gotten
rid of, with the area and power reduced according. The
050100150 200 25030035040
0
0
50
100
150
200
250
300
350
400
nz = 3200
Figure 4. Final generated random mapping matrix.

S. F. SHI ET AL.
90
decoding results including soft probability information
and the hard decision bits are fully bit match to the fixed
point simulation. During the arithmetic operation, all
variables are fixed point format. Besides, all decoder’s
input symbols are 16-bit vectors, and some intermediate
variable vectors are reached to 20 bits. Due to the all
pipelines, the throughput of our decoder has been greatly
improved compared with former RTL work in [1]. In our
RTL implementation, the clock consumption of horizontal
unit is 16 clock cycles per iteration, and 3 clock cycles
per iteration for vertical unit. If we set the iteration times
as 16, the decoder needs






16N/L3 N/L16 1904 
25Mbps
cycles to finish the decoding of a block with N = 400 bits
and L = 8. So the information throughput is about
in our hardware
implementation. Obviously, the throughput of our current
decoder is about 13 times higher than previous design
[1].
300MHz N/190463.0
Almost all the existing LDPC codes or RPC codes
hardware designs are fixed to a certain dimension matrix.
But in actual system, we sometimes need to change the
mapping matrix. So in configurable hardware architec-
ture, we may need many counters to generate enable-
signals. Also, in iteration decoding processing, we use
RAM memory to store the non-zero weights permutation
information and Probability information in every itera-
tion process.
In summary, the mapping matrix determines different
values of counter and the size of RAM memory in RTL
implementation. Figure 5 shows our configurable hard-
ware architecture design. So as to match all kinds dimen-
sion matrix, all counter values are corresponding to the
maximal dimension. In actual implementation, we have a
global reset-enable signal for RPC decoder. Before de-
coding, all the counters and RAM memory should be
initialized through the wishbone bus. Within the wishbone
bus, there is an address decoder for updating the counter
values. The wishbone bus is controlled by a peripherals
CPU. When data initialization has been completed, the
decoder begins to read receiving symbols and then starts
decoding. In order to realize configurable hardware im-
receive symbolsdecoder bits
Figure 5. Configurable hardware architecture.
plementation, the original matrix weights permutation
information saved in ROM memory should be converted
to RAM memory. The proposed configurable hardware
architecture is now under way.
5. Simulation Results
In this section, we evaluate the decoding performance of
the proposed matrix construction approach compared
with random permutation matrix and cyclic-shift map-
ping matrix. In detail, we will analyze the short girth, the
minimum code weight, bit error rate and data throughput
rate of the three mapping matrices.
5.1. Short Girth and Minimum Code Weight
In the following performance analysis, we define 400

random permutation matrix as Phix, the
400400 400

multilevel cyclic-shift mapping matrix as Gcs, and our
proposed matrix as Gqc with parameters x2

and
y3

.
Through calculation, we know that all the three matri-
ces’ short girth 4 and girth 6 are zero. But the minimum
code weight of random permutation matrix, cyclic-shift
matrix and quasi-cyclic matrix are respectively two, zero
and zero. So we can probably know that matrix Gqc will
not incur much performance degradation compared with
other two matrices. Since there is only one non-zero
weight in each sub matrix, the data allocator won’t be
needed. The general performance analysis will be
showed in next part.
5.2. Evaluation of BER and Throughput Rate
We test the BER performance of the three matrices in
AWGN channel state. The channel SNR in our simula-
tion is ranged from 1dB to 13dB. The BER performance
is shown in Figure 6.
0246810 12 14
10
-6
10
-5
10
-4
10
-3
10
-2
10
-1
10
0
SN R (d B)
BER
Phix
Gc s
Gqc
Figure 6. BER performance of different matrices.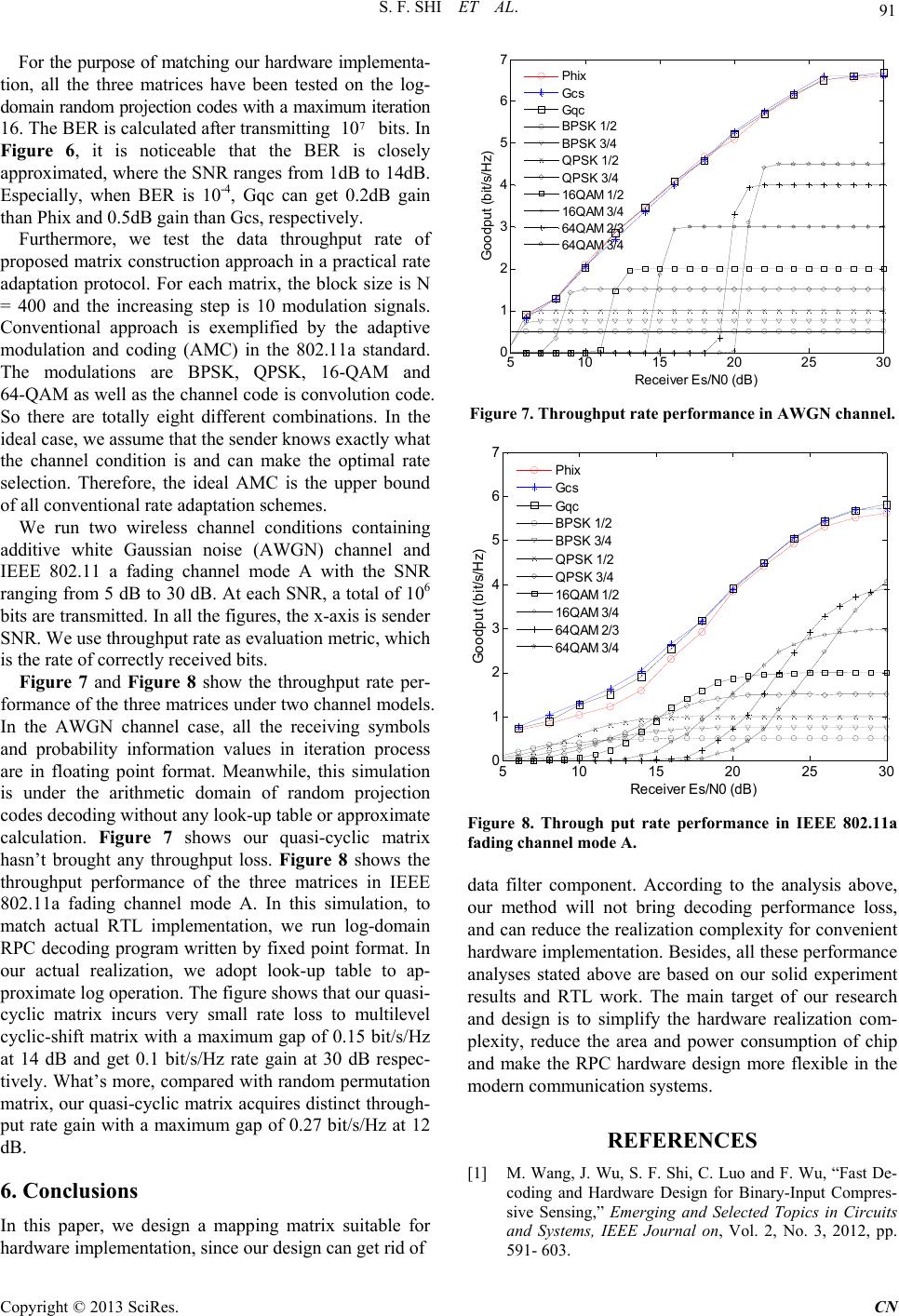

S. F. SHI ET AL. 91
For the purpose of matching our hardware implementa-
tion, all the three matrices have been tested on the log-
domain random projection codes with a maximum iteration
16. The BER is calculated after transmitting bits. In
Figure 6, it is noticeable that the BER is closely
approximated, where the SNR ranges from 1dB to 14dB.
Especially, when BER is 10-4, Gqc can get 0.2dB gain
than Phix and 0.5dB gain than Gcs, res pectively .
7
10
Furthermore, we test the data throughput rate of
proposed matrix construction approach in a practical rate
adaptation protocol. For each matrix, the block size is N
= 400 and the increasing step is 10 modulation signals.
Conventional approach is exemplified by the adaptive
modulation and coding (AMC) in the 802.11a standard.
The modulations are BPSK, QPSK, 16-QAM and
64-QAM as well as the channel code is convolution code.
So there are totally eight different combinations. In the
ideal case, we assume that the sender knows exactly what
the channel condition is and can make the optimal rate
selection. Therefore, the ideal AMC is the upper bound
of all conventional rate adaptation schemes.
We run two wireless channel conditions containing
additive white Gaussian noise (AWGN) channel and
IEEE 802.11 a fading channel mode A with the SNR
ranging from 5 dB to 30 dB. At each SNR, a total of 106
bits are transmitted. In all the figures, the x-axis is sender
SNR. We use throughput rate as evaluation metric, which
is the rate of correctly received bits.
Figure 7 and Figure 8 show the throughput rate per-
formance of the three matrices under two channel models.
In the AWGN channel case, all the receiving symbols
and probability information values in iteration process
are in floating point format. Meanwhile, this simulation
is under the arithmetic domain of random projection
codes decoding without any look-up table or approximate
calculation. Figure 7 shows our quasi-cyclic matrix
hasn’t brought any throughput loss. Figure 8 shows the
throughput performance of the three matrices in IEEE
802.11a fading channel mode A. In this simulation, to
match actual RTL implementation, we run log-domain
RPC decoding program written by fixed point format. In
our actual realization, we adopt look-up table to ap-
proximate log operation. The figure shows that our quasi-
cyclic matrix incurs very small rate loss to multilevel
cyclic-shift matrix with a maximum gap of 0.15 bit/s/Hz
at 14 dB and get 0.1 bit/s/Hz rate gain at 30 dB respec-
tively. What’s more, compared with random permutation
matrix, our quasi-cyclic matrix acquires distinct through-
put rate gain with a maximum gap of 0.27 bit/s/Hz at 12
dB.
6. Conclusions
In this paper, we design a mapping matrix suitable for
hardware implementation, since our design can get rid of
510 15 20 25 30
0
1
2
3
4
5
6
7
R eceiver Es/ N0 ( dB)
G oodput ( bit/s/Hz)
Phix
Gcs
Gqc
BPSK 1 /2
BPSK 3 /4
QPSK 1/2
QPSK 3/4
16QAM 1/2
16QAM 3/4
64QAM 2/3
64QAM 3/4
Figure 7. Throughput rate per formanc e in AWGN channel.
510 1520 25 30
0
1
2
3
4
5
6
7
R eceiv er Es/N0 ( dB)
Go odput (bi t /s /Hz)
Phix
Gcs
Gqc
BPSK 1/2
BPSK 3/4
QPSK 1/2
QPSK 3/4
16QAM 1/2
16QAM 3/4
64QAM 2/3
64QAM 3/4
Figure 8. Through put rate performance in IEEE 802.11a
fading channel mode A.
data filter component. According to the analysis above,
our method will not bring decoding performance loss,
and can reduce the realization complexity for convenient
hardware implementation. Besides, all these performance
analyses stated above are based on our solid experiment
results and RTL work. The main target of our research
and design is to simplify the hardware realization com-
plexity, reduce the area and power consumption of chip
and make the RPC hardware design more flexible in the
modern communication systems.
REFERENCES
[1] M. Wang, J. Wu, S. F. Shi, C. Luo and F. Wu, “Fast De-
coding and Hardware Design for Binary-Input Compres-
sive Sensing,” Emerging and Selected Topics in Circuits
and Systems, IEEE Journal on, Vol. 2, No. 3, 2012, pp.
591- 603.

S. F. SHI ET AL.
92
[2] J. D. Brown, S. Pasupathy and K. N. Plataniotis, “Adap-
tive Demodulation Using Rateless Erasure Codes,” IEEE
Transactions on Communications, Vol. 54, 2006, pp.
1574-1585. doi:10.1109/TCOMM.2006.881236
[3] A. Gudipati and S. Katti, “Automatic Rate Adaptation,”
In Proc. of ACM Hotnets, 2010.
doi:10.1145/1868447.1868461
[4] H. Cui, C. Luo, K. Tan, F. Wu and C. W. Chen, “Seam-
less Rate Adaptation for Wireless Networking,” in Proc.
of ACM MSWiM, 2011, pp. 437-446.
[5] G. Masera, F. Quaglio and F. Vacca, “Implementation of
a Flexible LDPC Decoder,” IEEE Transactions on Cir-
cuits and Systems II: Express Briefs, Vol. 54, No. 6, 2007,
pp. 542-546. doi:10.1109/TCSII.2007.894409
[6] Y. Chen and K. Parhi, “Overlapped Message Passing for
Quasi-cyclic Low-density Parity Check Codes,” IEEE
Transactions on Circuits and Systems I: Regular Papers,
Vol. 51, No. 6, 2004, pp. 1106-1113.
doi:10.1109/TCSI.2004.826194
[7] G. Masera, F. Quaglio and F. Vacca, “Implementation of
a Flexible LDPC Decoder,” Circuits and Systems II: Ex-
press Briefs, IEEE Transactions on, Vol. 54, No. 6, 2007,
pp. 542-546.doi:10.1109/TCSII.2007.894409
[8] A. Tarable, S. Benedetto and G. Montorsi, “Mapping
Interleaving Laws to Parallel Turbo and Ldpc Decoder
Architectures,” Information Theory. IEEE Transactions
on, Vol. 50, 2004, 2004, pp. 2002 - 2009.
[9] M. Mansour and N. Shanbhag, “A 640-mb/s 2048-bit
Programmable Ldpc Decoder Chip,” Solid-State Circuits,
IEEE Journal of, Vol. 41, 2006, pp. 684-698.
doi:10.1109/JSSC.2005.864133
[10] Z. Khan and T. Arslan, “Pipelined Implementation of a
Real Time Programmable Encoder for Low Density Par-
ity Check Code on a ReconFigureurable Instruction Cell
Architecture,” Design, Automation & Test in Europe
Conference & Exhibition, 2007. DATE '07, 16-20 April
2007, pp. 1-6.