Communications and Network, 2013, 5, 80-85
http://dx.doi.org/10.4236/cn.2013.53B2016 Published Online September 2013 (http://www.scirp.org/journal/cn)
Analysis of Multipath and CW Interference Effects on
GNSS Receivers with EMLP Discriminator
Bo Qu1, Jiaolong Wei1, Shuangna Zhang2, Liang Bi2
1Department of Electronic and Inform ation Engineering, Huazhong University of Science and Technology, China
2Space Star Technology Co. Ltd, China
Received May, 2013
ABSTRACT
Multipath and continuo us wave (CW) interference may cause severe performance degradation of global navig ation sat-
ellite system (GNSS) receivers. This paper analyzes the code tracking performance of early-minus-late power (EMLP)
discriminator of GNSS receivers in the presence of multipath and CW interference. An analytical expression of the code
tracking error is suggested for EMLP discriminator, and it can be used to assess the effect of multipath and CW inter-
ference. The derived expression shows that the combined effects include three components: multipath component; CW
interference component and the combined component of multipath and CW interference. The effect of these compo-
nents depends on some factors which can be classified into two categories: the receiving environment and the receiver
parameters. Numerical results show how these factors affect the tracking performances. It is shown that the proper re-
ceiver parameters can suppress the combined effects of multipath and CW interference.
Keywords: Multipath; Interference; GNSS; EMLP; Discriminator
1. Introduction
GNSS signal is very susceptibility to receiving environ-
ment [1-2]. Multipath is the dominant error source in
most GNSS applications. Therefore, multipath perform-
ance analysis plays a significant role in the analysis of
the code tracking performance of GNSS receivers. The
multipath error envelope (MEE) is a common way of
assessing the multipath performance of a given sig-
nal/receiver combination [3]. CW interference is typical
radio frequency interference (RFI) which is another
error source for GNSS receivers [4, 5]. Thepost-correlati
on effects of narrowband interference and partial-band
interference have been analyzed in [4, 6]. Reference [7]
suggested analytical expressions for GNSS receiver per-
formance such as the effective carrier-to-noise density
ratio, the code tracking error and the carrier phase track-
ing error for the receiver affected by CW interference.
Reference [8] presented the analytic expressions of the
code tracking error bound for the EMLP discriminator
and the dot-p roduct (DP) discriminator. The definition of
new families of curves named interference error envelope
(IEE) and interference running average (IRA) was pre-
sented, and these tools are able to assess the impact of
RF interference on different GNSS receivers [9].
The effects of multipath or interference have been
analyzed in the articles ab ove. However, if multipath and
interference exist at the same time, their effects on the
code tracking performance with EMLP discriminator are
not independent. However, the combined effects of mul-
tipath and CW interference haven’t been analyzed in
other papers. This paper analyzes the effects of multipath
and CW interference on the code tracking performance
of GNSS receivers. An analytical expression of the code
tracking error is suggested for EMLP discriminator, and
it can be used to assess the combined effect of multipath
and CW interference.
The rest of this paper is organized as follows. Signal
models are provided in Section 2. The analytical expres-
sion of the code tracking error for EMLP discriminator is
derived in Section 3. Section 4 shows how the receiving
environment and the receiver parameters affect the code
tracking error. This paper concludes in Section 5.
2. Signal Models
As defined in [10], the direct signal is denoted as equa-
tion(1):
000
()( )cos(2)
c
rt astft0



 (1)
with a0 being the amplitude of the direct signal, s(t) being
the pseudo random noise (PRN) code, τ0 being the time
delay, fc being the carrier frequency, and φ0 being the
carrier phase.
C
opyright © 2013 SciRes. CN

B. QU ET AL. 81
With the increase in the number of reflections, the am-
plitudes of reflected signals are becoming smaller and
smaller. Without loss of generality, one reflected signal
with the maximum amplitude is taken into consideration
to simplify the received signal model, so the reflected
signal can be simplified as follow:
11
()( )cos(2)
Nc
rt astft 1

   (2)
where a1 is the amplitude of a reflected signal, τ1 is the
time delay of a reflected signal, φ1 is the carrier phase of
a reflected signal.
The CW interference can be considered to be a sine
wave which can be expressed as:
() cos(22)
lcl
lt cftftl

 
1
l
(3)
where cl is the amplitude of CW interference, fl is the
frequency offset from the carrier frequency fc , and φl is
the phase of CW interference.
Therefore, the received signal can be expressed as:
00 0
11
()( )cos(2)
()cos(2)
cos(22)
c
c
lcl
rt astft
ast ft
cftft









 
 

(4)
Before processing the received signal and beginning
the code tracking, the received signal needs to be down-
converted. In the down converting process, the estimated
carrier phase is provided by the phase locked loop (PLL)
and a replica carrier is generated by the receiver. The
replica carrier is expressed as 0
ˆ
2cos(2 )
c
ft

, where
0
ˆ

is the estimated carrier phase. After down conv erting
and filtering the received signal, the received signal can
be expressed by the in-phase component and the quadra-
ture component. The in-phase component can be ex-
pressed as follow:
00 00
11 10
ˆ ()( )cos()
ˆ
()cos()cos(2)
I
lll
st ast
astc ft

0
ˆ

 
 
 
(5)
The quadrature component can be expressed as follow:
00 00
11 10
ˆ ()( )sin()
ˆˆ
()sin()sin(2)
Q
lll
st ast
astc ft 0




 
 
(6)
In the delay lock loop, the code generator usually gen-
erates two types of PRN codes: early replica code
, late replica code , where
0
*0
ˆ (st d  
ˆ/
2) /2)
*0
ˆ (st d  

is the estimated time delay, * denotes the conjugate
operation, and d is the correlator spacing. In the code
tracking process, the replica codes are multiplied and
integrated with the in-phase component and the quadra-
ture component.
The early in-phase output
E
I
can be expressed as
follow:
000
110 1
/2
*
00
/2
ˆ cos()()
2
ˆˆ
cos()()
2
ˆˆ
cos(2)()
2
p
p
E
T
l
ll I
pT
d
Ia R
d
aR
cd
f
tst
T


 
 





dt

(7)
Similarly, the late in-phase output
L
I
, the early quad-
rature output
E
Q and the late quadrature output
L
Q
can be expressed respectively as follow:
000
110 1
/2
*
00
/2
ˆ cos()()
2
ˆˆ
cos()()
2
ˆˆ
cos(2)()
2
p
p
L
T
l
ll
pT
d
Ia R
d
aR
cd
f
tst
T


 
 





dt

(8)
000
1011
/2
*
00
/2
ˆ sin()()
2
ˆˆ sin()()
2
ˆˆ
sin(2)()
2
p
p
E
T
l
ll
pT
d
Qa R
d
aR
cd
f
tst
T


 
 





dt

(9)
000
1011
/2
*
00
/2
ˆ sin()()
2
ˆˆ sin()()
2
ˆˆ
sin(2)()
2
p
p
L
T
l
ll
pT
d
Qa R
d
aR
cd
f
tst
T


 
 
 




dt

(10)
where
p
T is the integration time, 00
ˆ


  is the
code tracking error, and 110 ˆ



 is the extra delay of
the reflected signal with resp ect to th e d irect signal, ()R

is the autocorrelatio n function defined as follow:
/2
*
/2
1
()() ()
p
p
T
pT
Rstst
Tdt




 (11)
When CW interference is multiplied with the replica
PRN signal, the CW interference is spread by the PRN
code. Since the code tracking loop is an equivalent low-
pass filter, when the interference locates at zero fre-
quency (this occurs when c
/( )
lc
f
nNT), it causes the
most serious degradation of the code tracking perform-
ance. Then the interferenc e term of
E
I
can be expressed
as follow [8]:
_()cos(/ )
E
ll cc
I
cCndn NT   (12)
where 12/
0
() ()/
c
c
N
jmnN
p
mc
m
CnS nceNT



c

B. QU ET AL.
82
is the Fourier transform of the PRN signal, is the
transform of the pluse shape, ()
p
Sn
0
ˆˆ
=2(/
lc
nNT 0
)
c

   ,
and

is the phase of . Similarly, we can obtain
the interference term of ()Cn
L
I
,
E
Q, and
L
Q.
3. Code Tracking Performance Analysis
The EMLP discriminator is a typical noncoherent dis-
criminator which can mitigate the effect of the phase
difference between the carrier phase and the estimated
carrier phase. The output of EMLP discriminator is de-
noted as follow:
22 22
()()
E
MLPE EL L
DIQIQ  (13)
Assuming that the carrier tracking loop tracks the car-
rier phase of the received signal perfectly, we can obtain
00
ˆ

 . Substituting (7)-(10) into (13) and simplifying
the expression, we can obtain the following expression.
_
()() ()
()()
EMLPDirect Mult
InferMult Infer
DDD
DD








 (14)
The output of EMLP discriminator includes four
components: the direct signal component ()
Direct
D


, the
multipath component ()
Mult
D


, the CW interference
component ()
Infer
D


, and the combined component
_MultInfer(D)


of multipath and CW interference.
The direct signal component ()
Direct
D


can be ex-
pressed as follow:
22 2
0
()() ()
22
Direct
d
DaR R






d
(15)
The direct signal component has relation to the ampli-
tude of the direct signal a0, the correlator spacing d, and
the autocorrelation function of the navigation signal. The
direct signal component is the output of EMLP discrimi-
nator without the effects of multipath and CW interfer-
ence.
The multipath component ()
Mult
D


can be ex-
pressed as follow:
22 2
_11 1
01 11
1
ˆˆ ()() ()
22
ˆˆ 2c o s ()()()
22
ˆ ()()
22
MultEMLP
dd
DaR R
dd
aaR R
dd
RR
 



 










 


(16)
In addition to the amplitude of the direct signal a0, the
correlator spacing d and the autocorrelation function of
the navigation signal, equation (16) shows that the mul-
tipath component ()
Mult
D


has relation to the ampli-
tude a1 of the reflected signal, the phase difference of the
reflected signal and the direct signal, and the extra delay
of the reflected signal with respect to the direct signal 1
ˆ

.
When only multipath signal exists in the receiving envi-
ronment, the output of EMLP discriminator is the sum of
the multipath component ()
Mult
D


and the direct signal
component ()
Direct
D


.
The CW interference component ()
Infer
D


can be
expressed as follow:
0
0
()2
(
+2
(
cos()cos( /)
)()
22
sin()sin(/)
)()
22
I
nfecwc c
cwc c
A dnNT
dd
RR
dnNT
dd
RR















r
Da
aA


(17)
CW interference component D( )
Infer


ˆ 2 (/nNT
has relation to
the phase 00 =
lcc
ˆ)
 


  , the amplitude
and the frequency of CW interference beside the ampli-
tude of the direct signal a0, the correlator spacing d and
the autocorrelation function of the navigation signal. It is
easy to know that the output of EMLP discriminator is
the sum of the CW interference component Infer(D)


and the direct signal component (
Direct
D)


in the case
that only CW interference exists in the receiving envi-
ronment.
The combined component _()
Mult Infer
D


of multipath
and CW interference can be expressed as equation (18).
__
2c
2s
Mult Infer
cw
cw
D
aA
aA
11
11
11
11
( )
ˆ
os( )cos(/)
ˆˆ ()()
22
ˆ
in( )sin(/)
ˆˆ ()()
22
EMLP
c c
c c
dn NT
dd
RR
dn NT
dd
RR




 

 








(18)











The combined component _()
Mult Infer
D


has relation
to not only the multipath factors but also the CW inter-
ference factors. Because of the combined component
_MultInfer (D)


, the effects of multipath and CW interfer-
ence are not independent.
The tracking error is usually small, so ()
EMLP
D


can
be linearly expressed as follow:
'
(0) (0)
EMLP EMLP
DD D

 ()
EMLP (19)
The tracking error


can be expressed as
'
(0)
(0)
EMLP
EMLP
D
D

 (20) 
In order to simplify the mathematic derivation of the
tracking error, some functions are defined as equations
(21)-(24).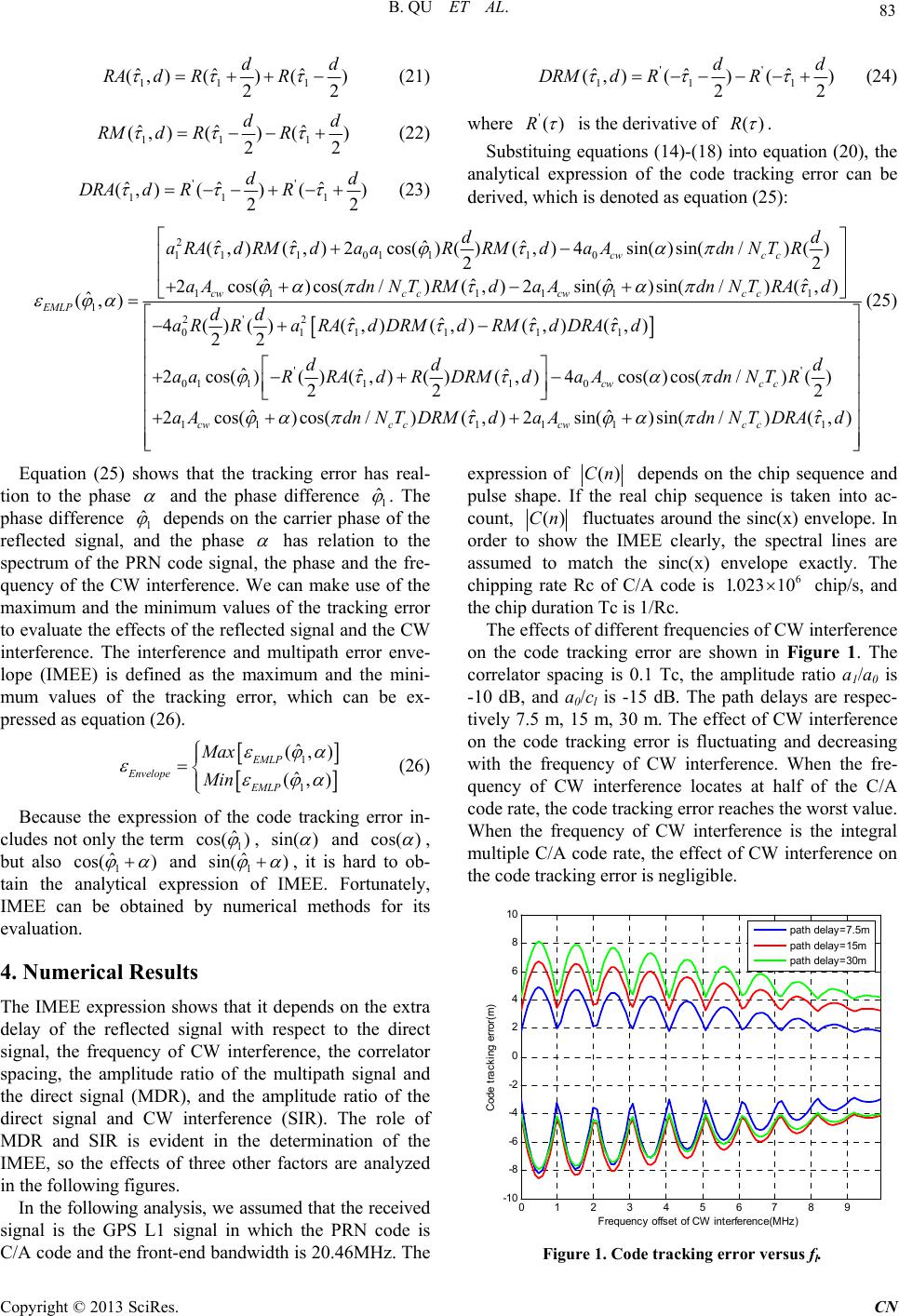

B. QU ET AL.
83
''
11 1
ˆˆˆ (,)() ()
22
dd
DRMd RR    (24)
11 1
ˆˆˆ (,)() ()
22
d
RA dRR   
d
(21)
11 1
ˆˆˆ
(,)() ()
22
d
RMdRR
  
d
(22) where '()R

is the derivative of ()R

.
Substituing equations (14)-(18) into equation (20), the
analytical expression of the code tracking error can be
derived, which is denoted as equation (25):
''
11 1
ˆˆˆ (,)() ()
22
dd
DRA dRR    (23)
2
11101110
11111 1
12' 2
01
ˆ ˆˆ ˆ
(,) (,)2cos()() (,)4sin()sin(/)()
22
ˆˆ ˆˆ
2cos()cos(/)(, )2sin()sin(/)( , )
ˆ
(,)
4()()
22
cwc c
cwc ccwc c
EMLP
dd
aRAdRMdaaRRMdaAdn NTR
aAdn NT RMdaAdn NT RAd
dd
aRRa R
 
 

 

 
 
 
 



11 11
' '
01 1110
11111 1
ˆˆˆˆ
(,)(,)(,) (,)
ˆˆˆ
2cos()( )( , )()( , )4cos()cos(/)()
22
ˆˆ ˆˆ
2cos()cos(/)( , )2sin()sin(/)(,
cwc c
cwcc cwcc
A dDRMdRMdDRA d
dd
aaRRAdRDRMdaAdn NT R
a AdnN TDRMda AdnN TDRA
 
 
 


 


 
2
d
)d
 
 
 
 
 
 
 
 
 
(25)
Equation (25) shows that the tracking error has real-
tion to the phase

and the phase difference 1
ˆ

. The
phase difference 1
ˆ

depends on the carrier phase of the
reflected signal, and the phase

has relation to the
spectrum of the PRN code signal, the phase and the fre-
quency of the CW interference. We can make use of the
maximum and the minimum values of the tracking error
to evaluate the effects of the reflected signal and the CW
interference. The interference and multipath error enve-
lope (IMEE) is defined as the maximum and the mini-
mum values of the tracking error, which can be ex-
pressed as equation (26).



1
1
ˆ
(,)
ˆ
(,)
EMLP
Envelope
EMLP
Max
Min










 (26)
Because the expression of the code tracking error in-
cludes not only the term 1
ˆ
cos( )

, sin( )

and cos( )

,
but also 1
ˆ
cos( )

  and 1
ˆ
sin( )

 , it is hard to ob-
tain the analytical expression of IMEE. Fortunately,
IMEE can be obtained by numerical methods for its
evaluation.
4. Numerical Results
The IMEE expression shows that it depends on the extra
delay of the reflected signal with respect to the direct
signal, the frequency of CW interference, the correlator
spacing, the amplitude ratio of the multipath signal and
the direct signal (MDR), and the amplitude ratio of the
direct signal and CW interference (SIR). The role of
MDR and SIR is evident in the determination of the
IMEE, so the effects of three other factors are analyzed
in the following figures.
In the following analysis, we assumed that the received
signal is the GPS L1 signal in which the PRN code is
C/A code and the front-end bandwidth is 20.46MHz. The
expression of ()Cn depends on the chip sequence and
pulse shape. If the real chip sequence is taken into ac-
count, ()Cn fluctuates around the sinc(x) envelope. In
order to show the IMEE clearly, the spectral lines are
assumed to match the sinc(x) envelope exactly. The
chipping rate Rc of C/A code is chip/s, and
the chip duration Tc is 1/Rc.
6
1.023 10
The effects of different frequencies of CW interference
on the code tracking error are shown in Figure 1. The
correlator spacing is 0.1 Tc, the amplitude ratio a1/a0 is
-10 dB, and a0/cl is -15 dB. The path delays are respec-
tively 7.5 m, 15 m, 30 m. The effect of CW interference
on the code tracking error is fluctuating and decreasing
with the frequency of CW interference. When the fre-
quency of CW interference locates at half of the C/A
code rate, the code tracking error reaches the worst value.
When the frequency of CW interference is the integral
multiple C/A code rate, the effect of CW interference on
the code tracking error is negligible.
0123456789
-10
-8
-6
-4
-2
0
2
4
6
8
10
Frequenc y offset of CW interference(M Hz )
Code tracking error(m)
pat h delay=7. 5m
pat h delay=15m
pat h delay=30m
Figure 1. Code tracking error versus fl.

B. QU ET AL.
84
The effects of different path delays on IMEE are
shown in Figure 2. The correlator spacing is 0.1 Tc, the
amplitude ratio a1/a0 is -10 dB, and a0/cl is -15 dB. The
frequencies of CW interference are respectively 0MHz,
0.5 MHz, 1 MHz, 1.5 MHz. The impact of multipath on
tracking error increases, when the time delay of multi-
path signal increases from 0m. However, when the IMEE
reaches the corresponding value, around which IMEE
fluctuates slightly. Since the chipping duration of C/A
code is 1/Rc and the path delay of 1 Tc is approximately
293 m. When the time delay of multipath is larger than
293 m, the multipath effect is suppressed due to the au-
tocorrelation of C/A code.
The effects of the correlator spacing on the code
tracking error are shown in Figure 3 and Figure 4. The
amplitude ratio a1/a0 is -10 dB, a0/cl is -15 dB, and the
correlator spacing are respectively 0.1 Tc, 0.3 Tc, and 0.5
Tc.
050100 150 200 250 300 350 400
-10
-8
-6
-4
-2
0
2
4
6
8
10
P at h del ay of reflected signal(m)
Code t racking error(m)
fl =0MH z
fl =0.5MHz
fl =1MH z
fl =1.5MHz
Figure 2. Code tracking error versus the path delay.
0123456789
-60
-40
-20
0
20
40
60
Frequency offset of CW in t erferenc e(M Hz )
Code t racking error(m)
d=0.1Tc
d=0.3Tc
d=0.5Tc
Figure 3. Code tracking error versus fl with different correla-
tor spacings.
050100150200 250 300 350 400
-80
-60
-40
-20
0
20
40
60
Path delay of reflec ted signal(m)
Code trac k ing error(m)
d= 0.1Tc
d= 0.3Tc
d= 0.5Tc
Figure 4. Code tracking error versus the path delay of the
reflected signal with different correlator spacings.
5. Conclusions
The effects of CW interference and multipath on EMLP
discriminator are analyzed in this paper. In the analysis,
an analytical expression of the code tracking error is
suggested for the EMLP discriminator, and it can be used
to assess the combined effect of multipath and CW inter-
ference. The analytical expression of the code tracking
error shows that the code tracking performance can be
improved by shortening the correlator spacing for the
receiver. Further, the analytical expression shows that the
combined effects of CW interference and multipath on
code tracking performance depend on many factors.
When the frequency of CW interference locates at inte-
gral times of PRN code rate, the CW interference can be
suppressed. When the frequency of CW interference is
the sum of half of the C/A code rate and integral times of
PRN code rate, the code tracking error reaches the worst
value. The effects of multipath on EMLP increases as the
time delay of the reflected signal increases, and then it
fluctuates with a value until the time delay is larger than
the sum of half of the correlator spacing and the ch ipping
duration. When the time delay is larger than the sum of
half of the correlator spacing and the chipping duration,
the effect of multipath is suppressed by the code tracking
loop.
6. Acknowledgements
This work was supported by the National High Technol-
ogy Research and Development Program of China (863
Program). The fund number is 2011AA120503.
REFERENCES
[1] P. Misra and P. Enge, “Global Positioning System, Sig-

B. QU ET AL.
85
nals, Measurements and Performance,” Second Edition,
Ganga Jumuna Press, Lincoln, 2006.
[2] E. D. Kaplan and C. J. Hegarty, “Understanding GPS:
Principles and Applications,” 2th Edition, Artech House
Inc., Norwood, 2006.
[3] M. Irsigler, J. A. Avila-Rodriguez and G. Hein, “Criteria
for GNSS Multipath Performance Assessment,” Pro-
ceedings of the 18th International Technical Meeting of
the Satellite Division of the Institute of Navigation, Long
Beach, 14-16 September 2005, pp. 2166-2177.
[4] J. W. Betz, “Effect of Narrowband Interference on GPS
Code Tracking Accuracy,” Proceedings of the 2000 Na-
tional Technical Meeting of The Institute of Navigation,
Anaheim, 26-28 January 2000, pp. 16-27.
[5] A. T. Balaei, A. G. Dempster and L. L. Presti, “Charac-
terization of the Effects of CW and Pulse CW Interfer-
ence on the GPS Signal Quality” IEEE Transactions on
Aerospace and Electronic Systems, Vol. 45, No. 4, 2009,
pp. 1418-1431. doi:10.1109/TAES.2009.5310308
[6] J. W. Betz, “Effect of Partial-Band Interference on Re-
ceiver Estimation of C/N0: Theory,” Proceedings of the
2001 National Technical Meeting of The Institute of Na-
vigation, Long Beach, 22-24 January 2001, pp. 817-828.
[7] J. Jang, M. Paonni and B. Eissfeller, “CW Interference
Effects on Tracking Performance of GNSS Receivers,”
IEEE Transactions on Aerospace and Electronic Systems,
Vol. 48, No. 1, 2012, pp. 243-258.
doi:10.1109/TAES.2012.6129633
[8] Y. Liu, Y. Ran, T. Ke and X. Hu, “Code Tracking Per-
formance Analysis of GNSS Signal in the Presence of
CW Interference,” Signal Processing, Vol. 91, No. 4,
2011, pp. 970-987. doi:10.1016/j.sigpro.2010.09.022
[9] B. Motella, S. Savasta, D. Margaria and F. Dovis, “Me-
thod for Assessing the Interference Impact on GNSS Re-
ceivers,” IEEE Transactions on Aerospace and Electronic
Systems, Vol. 47, No. 2, 2011, pp. 1416-1431.
doi:10.1109/TAES.2011.5751267
[10] Y. Yang, R. R. Hatch and R. T. Sharpe, “GPS Multipath
Mitigation in Measurement Domain and Its Applications
for High Accuracy Navigation,” Proceedings of the 17th
International Technical Meeting of the Satellite Division
of The Institute of Navigation, Long Beach, 21-24 Sep-
tember 2004, pp. 1124-1130.